《算法系列》之队列与堆

简介

  队列和堆也是基础的数据结构，无论刷不刷题都需要了解的数据结构。其中堆可以看做是优先队列，在很多语言中，都有优先队列或者说堆的的容器可以直接使用，但是在面试中，面试官更倾向于让更面试者自己实现一个堆。所以建议读者掌握大小根堆的实现方法，尤其要搞懂建堆、调整和删除的过程。

理论基础

  队列（Queue）是一种先进先出（FIFO，First-In-First-Out）的线性表。和栈一样，队列是一种操作受限制的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（称为 rear）进行插入操作，在前端（称为 front）进行删除操作。队列的学习可以类比栈。队列是实现广度优先搜索的重要数据结构。

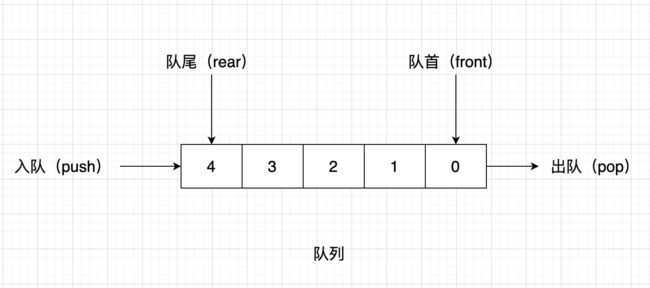
基于链表实现队列：

public class Queue implements Iterable{
    
    private Node head;
    private Node last;
    private int N;

		// 内部类
    private class Node{  
   		  // 链表所存元素
        public T item; 
        public Node next;

				// Node的有参构造
        public Node(T item,Node next){
            this.item=item;
            this.next=next;
        }
    }

		// 队列的构造
    public Queue(){ 
    		// head结点不存储元素
        this.head=new Node(null,null); 
        this.last=null;
        this.N=0;
    }


    public boolean isEmpty(){
        return N==0;
    }


    public int size(){
        return N;
    }

    // 尾插
    public void enqueue(T t){
    // 尾结点为null
    if(last==null){ 
        last=new Node(t,null);
        head.next=last;
    }else{ 
    		// 尾结点不为null
    		// 记录旧尾结点
        Node oldlast=last;
        // 更新尾结点
        last=new Node(t,null); 
        // 旧的尾结点指向新的尾结点
        oldlast.next=last;
    }
        N++;
    }

    // 头取
    public T dequeue(){
    if(isEmpty()){
        return null;
    }else{
    		// 旧的首结点的下一个结点
        Node oldFirst=head.next;
        // 更新首结点的下一个结点
        head.next=oldFirst.next;
        N--;
        // 因为取元素是在删除，如果删完了就需要重置last=null
        if(isEmpty()){
            last=null;
        }
        // 先进先出，头取
        return oldFirst.item;
        }
    }

    @Override
    public Iterator iterator() {
        return new MyIterator();}

    private class MyIterator implements Iterator{
    		// 记录每次遍历的结点
        private Node n;

        MyIterator(){
            this.n=head;
        }

        @Override
        public boolean hasNext() {
            return n.next!=null;
        }

        @Override
        public Object next() {
            n=n.next;
            return n.item;
        	}
        }

    public static void main(String[] args) {
        Queue q=new Queue();
        q.enqueue("a");
        q.enqueue("b");
        q.enqueue("c");
        q.enqueue("d");

        for(String k:q){
            System.out.println(k);
        }
        // 删除一个元素（先进先出）
        System.out.println(q.dequeue()); 
        for(String k:q){
            System.out.println(k);
        }
    }
}

  堆(Heap)是计算机科学中一类特殊的数据结构，是最高效的优先级队列。 堆通常是一个可以被看做一棵完全二叉树的数组对象。 堆是非线性数据结构，相当于一维数组，有两个直接后继。将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。堆总是满足下列性质：

• 堆中某个结点的值总是不大于或不小于其父结点的值。
• 堆总是一棵完全二叉树。
  
  基于数组实现大顶堆：

public class MyPriorityQueue {
    
    public static void shiftDown(int[] arr,int parent){
        // 首先的记录孩子的节点位置，parent元素的下表是0
        // 左孩子节点的下标是2*parent + 1只需要记录左孩子的节点位置即可,如果父节点的值,大于子节点的值
        // 需要将节点进行交换，交换的时候，是将两个子节点中最小的节点进行交换
        int child = 2* parent + 1;
        // 记录数组长度,也就是堆的长度
        int size = arr.length;
        while (child < size){
            // 找到节点中的最大值
            if(child + 1 < size && arr[child] < arr[child + 1]){
                child = child + 1;
            }
            // 找到之后将节点进行交换
            if(arr[parent] < arr[child]){
                int temp = arr[parent];
                arr[parent] = arr[child];
                arr[child] = temp;
            }else {
                // 此时不用进行调整
                break;
            }
            // 完成之后让节点parent指向子节点继续向下执行
            parent = child;
            child = 2*parent + 1;

        }
     }

    public static void shiftUp(int[] arr, int child) {
    	// 父节点的元素下标正是child - 1 再除以2
        int parent = (child-1) / 2;
        while (child > 0){
            // 大堆的方式,把子节点向上调整
            if(arr[parent] < arr[child]){
                int temp = arr[parent];
                arr[parent] = arr[child];
                arr[child] = temp;
            }else {
                break;
            }
            child = parent;
            parent = (child-1) / 2;
        }
    }

    // 建堆操作
    public static void createHeap(int[] array){
        for(int i = (array.length - 1 -1) / 2; i >= 0;i--){
            shiftDown(array,i);
        }
    }

    private int[] arr = new int[100];
    // 记录对的元素个数
    private int size = 0;
    // 往堆中插入元素

    public void offer(int val){
        if(size >= arr.length){
            return;
        }
        arr[size] = val;
        size ++;
        // 插入之后,需要将元素进行向上调整
        // 将刚插入的最后一个元素向上调整
        shiftUp(arr, size-1);

    }

    // 获取堆顶元素
    public Integer peek(){
        if(size == 0){
            return null;
        }
        return arr[0];
    }

    // 删除操作,一定是删除堆顶元素
    public Integer poll(){
        if(size == 0){
            return null;
        }
        // 获取堆顶元素
        int popElement = arr[0];
        // 和堆的最后一个元素进行交换
        int temp = popElement;
        popElement = arr[size -1];
        arr[size - 1] = popElement;

        // 交换完成之后,删除即可
        size--;

        // 删除之后，进行shiftUp操作
        shiftUp(arr, size - 1);
        return popElement;
    }

解题心得

• 单纯的队列与堆的题其实并不算多，但我们仍要重点了解这两种基础数据结构。
• 堆排序在很多大公司的面试中很常见，需要重点学习。
• 队列在广度优先搜索中很有用。
• 这里的堆是指数据结构，和操作系统的“堆栈”概念是两种概念。
• 堆可以看做是优先队列。
• 堆通常是一个可以被看做一棵完全二叉树的数组对象。

算法题目

215. 数组中的第K个最大元素

题目解析：我们也可以使用堆排序来解决这个问题，即建立一个大根堆，做 k - 1次删除操作后堆顶元素就是我们要找的答案。
代码如下：

/**
 * 基于堆排序的选择方法
 */
 class Solution {
    public int findKthLargest(int[] nums, int k) {
        int heapSize = nums.length;
        buildMaxHeap(nums, heapSize);
        for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
            swap(nums, 0, i);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }
        return nums[0];
    }

    public void buildMaxHeap(int[] a, int heapSize) {
        for (int i = heapSize / 2; i >= 0; --i) {
            maxHeapify(a, i, heapSize);
        } 
    }

    public void maxHeapify(int[] a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a, i, largest);
            maxHeapify(a, largest, heapSize);
        }
    }

    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

218. 天际线问题

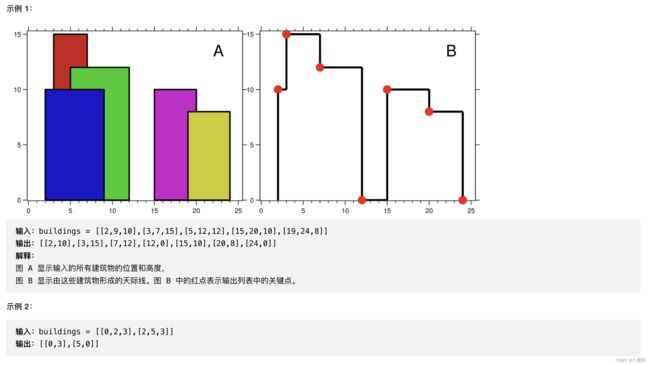
题目解析：如果将所有的建筑的边界作为一条线，那么所有的答案都在这些线上。考虑任意一条线，那么这条线和所有相交的建筑（这里排除掉刚好和建筑右边界相交），取一个最高的高度，然后判断这个高度是否和ans末尾最后一个元素的高度相等，不相等就加入进去，在这里为了快速得到最高的高度，使用一个堆来进行记录。
代码如下：

/**
 * 扫描线 + 优先队列
 */
class Solution {
public List> getSkyline(int[][] buildings) {
        // 得到所有由建筑边界构成的边界线，并升序
        int[] boundaries = new int[buildings.length * 2];
        for (int i = 0; i < buildings.length; i++) {
            boundaries[2 * i] = buildings[i][0];
            boundaries[2 * i + 1] = buildings[i][1];
        }
        Arrays.sort(boundaries);

        // 创建一个堆，维护一个边界-高度值对
        PriorityQueue pq = new PriorityQueue<>((a, b) -> b[1] - a[1]);

        List> ans = new ArrayList<>(); // 返回答案
        int index = 0; // 指向buildings
        for (int boundary : boundaries) {
            // 对于一个建筑，如果其左边界在当前判断的边界线左边或重叠，那么向堆加入右边界-高度值对
            while (index < buildings.length && buildings[index][0] <= boundary) {
                pq.offer(new int[] { buildings[index][1], buildings[index][2] });
                index++;
            }

            // 对于那些加入了堆中的建筑，从堆的顶部移出建筑右边界在边界线左边或重叠的边界-高度值对
            while (!pq.isEmpty() && pq.peek()[0] <= boundary) {
                pq.poll();
            }

            // 经过上面的两步操作之后，当前边界线穿过的建筑（不含右边界）全都在堆中，并且堆的顶端是所有穿过的建筑中，高度最高的，也就是天际线高度
            // 如果此时的堆为空，证明边界线没有穿过任何建筑，来到了建筑的分割位置，天际线为0
            int maxHeight = pq.isEmpty() ? 0 : pq.peek()[1];

            // 按照这种算法，每一条边界线都会产生一个天际线高度，如果这个高度和ans末尾元素的高度一致，那么就说明两条边界线穿过了同一个建筑，并且相邻，那么按照规则只取最左端
            if (ans.size() == 0 || maxHeight != ans.get(ans.size() - 1).get(1)) {
                ans.add(Arrays.asList(boundary, maxHeight));
            }
        }

        return ans;
    }
}

225. 用队列实现栈

题目解析：这题多少有点多此一举的感觉，为了满足栈的特性，即最后入栈的元素最先出栈，在使用队列实现栈时，应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作，其中 queue1用于存储栈内的元素，queue2作为入栈操作的辅助队列。
代码如下：

/**
 * 两个队列
 */
class MyStack {
    Queue queue1;
    Queue queue2;

    /** Initialize your data structure here. */
    public MyStack() {
        queue1 = new LinkedList();
        queue2 = new LinkedList();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue2.offer(x);
        while (!queue1.isEmpty()) {
            queue2.offer(queue1.poll());
        }
        Queue temp = queue1;
        queue1 = queue2;
        queue2 = temp;
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue1.poll();
    }
    
    /** Get the top element. */
    public int top() {
        return queue1.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue1.isEmpty();
    }
}

回到首页

刷 leetcode 500+ 题的一些感受

下一篇

《算法系列》之并查集