GCN学习笔记_01
GNN学习笔记
1 基本定义与概念
1.1 点、边、图
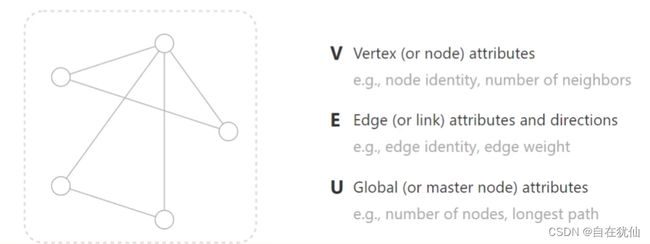
点:特征(人、实物…)
边:联系/关系(特征)
图:全局特征
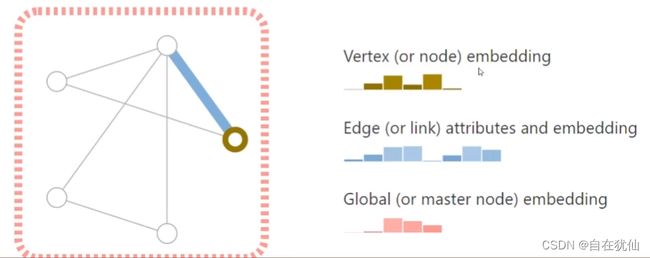
图神经网络的目标:整合特征、重构点边和图。首先就需要进行embedding
输出结果:点分类回归、边分类回归、图的分类回归
1.2 表示图的方法
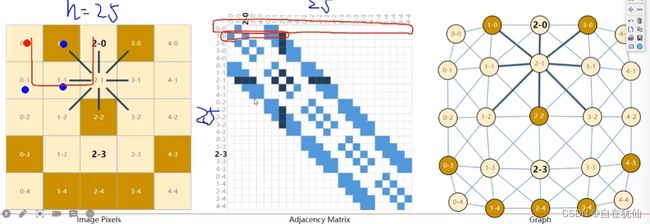
n*n的关系:邻接矩阵
表示谁与谁的关系,怎么相连的,即邻居之间的关系
邻接矩阵的保存其实不是N*N的,而是Source->Target:【(0,1),(2,0)】
建模的过程:
GNN(A,X)-- A:邻接矩阵,X:点的特征
图的邻接矩阵同样适合于文本,表示词与词之间的关系
GNN可以适用于什么领域?可能是创新点
- 图像和文本中
- 文本固定的长度和词向量其实不需要特殊的邻接矩阵
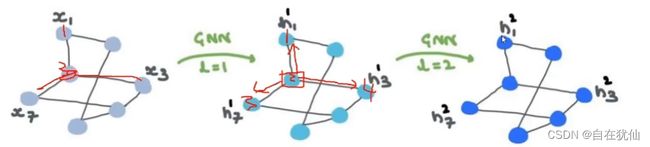
消息传递过程:
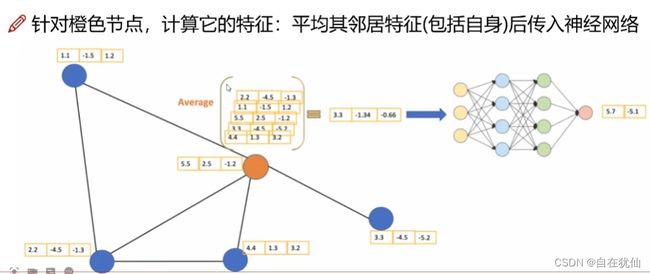
每个点如何更新:不仅考虑自身还得考虑邻居的信息
消息传递的方式:
- 求和
- 求平均
- 求最大/最小贡献
多层GNN:
GNN的本质是更新各个部分的特征,其中输入是特征,输出也是特征,邻接矩阵也不会变。多个层就是对全局关系的整合。
可以用来干什么:
- 多个点特征的整合:图分类
- 节点分类
- 边的分类
- …
1.3 GCN
半监督学习:在图中,有部分点没有标签,比如交通流量有的地方没有标签,同样可以进行预测。用少量标签也可以进行训练,但是计算损失的时候只用有标签的。
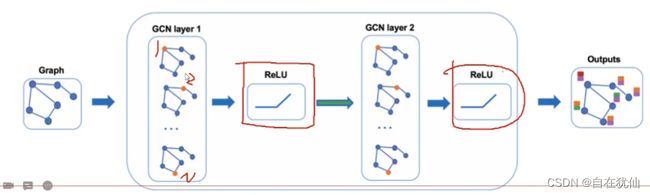
基本思想:
图卷积跟卷积类似,也是可以做多层的,每一层的输入的还是节点特征,然后将当前特征与网络结构图继续传入下层就可以不断计算。
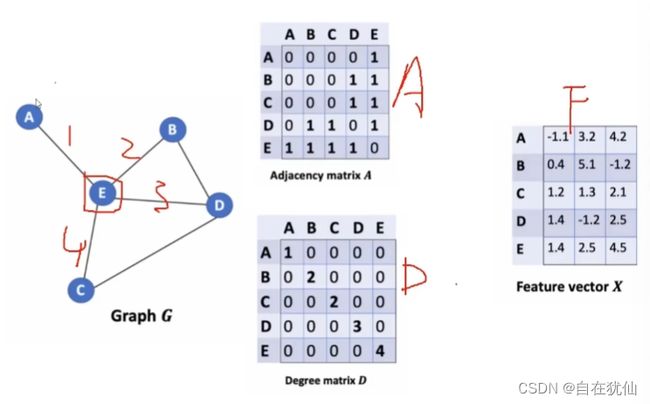
图的组成:
- G:图
- A:邻接矩阵
- D:节点的度,每个点和多少个点有关系,这就是度,比如E和四个点有关,所以是4
- F:每个节点的特征
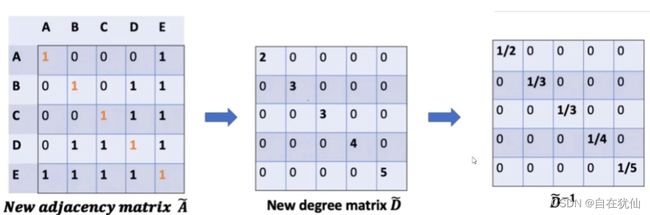
邻接矩阵的变换:
A ^ = A + λ I N \hat{A} = A + \lambda I_{N} A^=A+λIN
度矩阵的变换:实际是一种平均的概念
D ^ − 1 \hat{D}^{-1} D^−1
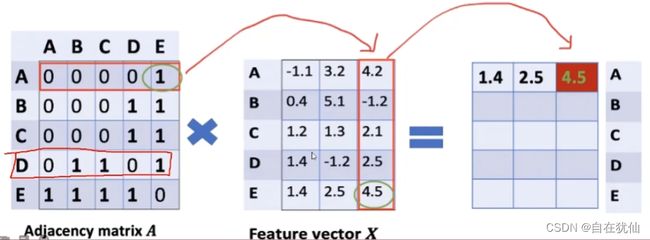
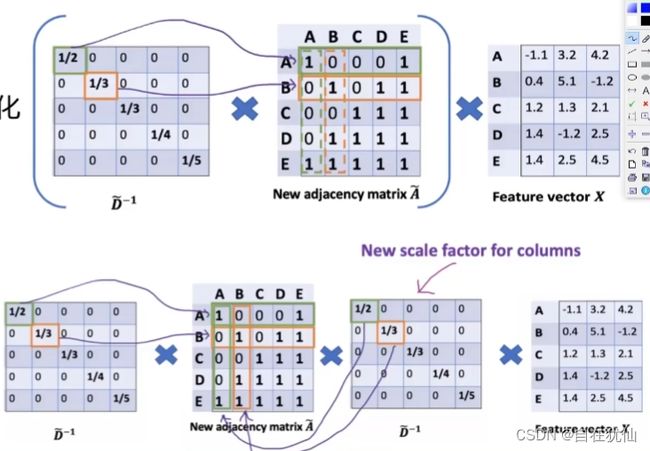
整体的计算流程:
D ^ − 1 ( A ^ X ) = ( D ^ − 1 A ^ ) X \hat{D}^{-1} (\hat{A}X) = (\hat{D}^{-1} \hat{A})X D^−1(A^X)=(D^−1A^)X
其中的 D ^ − 1 \hat{D}^{-1} D^−1实际就是相当于scale的方法,相当于对行的归一化操作
需要对列也进行归一化:
( D ^ − 1 A ^ D ^ − 1 ) X (\hat{D}^{-1} \hat{A}\hat{D}^{-1})X (D^−1A^D^−1)X
但这进行了两边归一化,所以这里只需要进行1/2次幂:
( D ^ − 1 / 2 A ^ D ^ − 1 / 2 ) X (\hat{D}^{-1/2} \hat{A}\hat{D}^{-1/2})X (D^−1/2A^D^−1/2)X
双层GCN示例:
2 pytorch基础代码实战
model.py
import torch_geometric.nn as nn
import torch
class GCN(torch.nn.Module):
def __init__(self,n_features,n_classes):
super(GCN, self).__init__()
self.GCN1 = nn.GCNConv(n_features,4)
self.GCN2 = nn.GCNConv(4, 4)
self.GCN3 = nn.GCNConv(4,2)
self.projection = nn.Linear(2,n_classes)
def forward(self,x,edge_index):
h = self.GCN1(x,edge_index)
h = h.tanh()
h = self.GCN2(h,edge_index)
h = h.tanh()
h = self.GCN3(h, edge_index)
h = h.tanh()
out = self.projection(h)
return out,h
if __name__ == '__main__':
model = GCN(34,4)
print(model)
visualization.py
from torch_geometric.datasets.karate import KarateClub
import networkx as nx
import matplotlib.pyplot as plt
from torch_geometric.utils.convert import to_networkx
# 导入benchmark数据集
def get_data():
datasets = KarateClub()
# print(data.data) # Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])
data = datasets[0]
print('输入样本(x,f):',data.x.shape)
print('标签:',data.y.shape)
print('邻接矩阵:',data.edge_index.shape)
print('半监督标签的mask:',data.train_mask.shape)
G = to_networkx(data)
visualize_graph(G,color=data.y)
return data,datasets.num_features
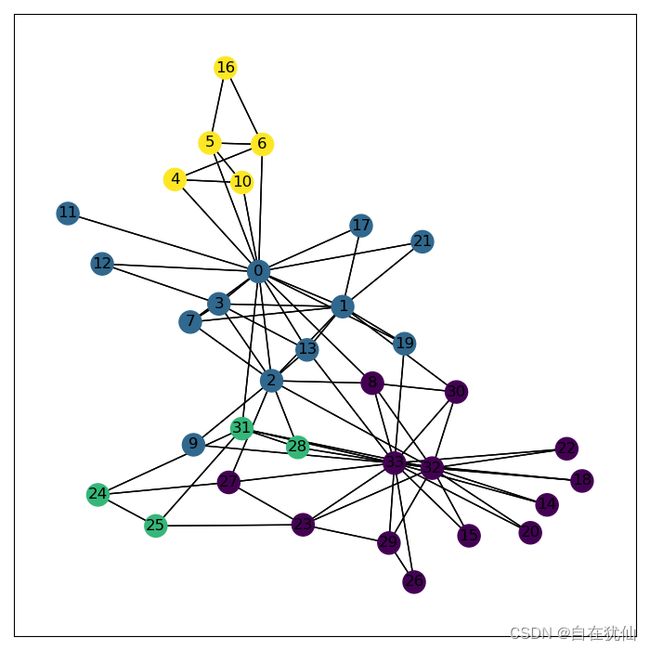
# 图的可视化
def visualize_graph(G,color):
plt.figure(figsize=(7,7))
plt.xticks([])
plt.yticks([])
nx.draw_networkx(G,pos=nx.spring_layout(G,seed=34),arrows=False,with_labels=True,node_color=color)
plt.show()
# 中间层的可视化
def visualize_embedding(H,color,epochs=None,loss=None):
plt.figure(figsize=(7,7))
plt.xticks([])
plt.yticks([])
plt.scatter(H[:,0],H[:,1],s=15,c=color)
if (epochs is not None) and (loss is not None):
plt.title(f'epoch:{epochs} loss:{loss}')
plt.show()
if __name__ == '__main__':
get_data()
train.py
import torch
from model import GCN
from visualization import visualize_embedding,get_data
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
def train(epochs:int,model,optim,criterion,data):
x = data.x
def epoch_train(train_x):
optim.zero_grad()
out,h = model(train_x,data.edge_index)
loss = criterion(out[data.train_mask],data.y[data.train_mask])
loss.backward()
optim.step()
return out,h,loss
for epoch in range(epochs):
out,h,loss = epoch_train(x)
print(f'epoch:{epoch+1} loss:{loss.sum()}')
if (epoch+1) % 100 == 0:
h = h.detach().cpu()
visualize_embedding(h,data.y)
def main():
data,num_features = get_data()
GCN_model = GCN(num_features,4)
optim = torch.optim.Adam(GCN_model.parameters(),lr=0.1)
criterion = torch.nn.CrossEntropyLoss()
epochs = 400
train(epochs,GCN_model,optim,criterion,data)
main()