3D软渲染器记录
GitHub地址:https://github.com/Khasehemwy/SoftwareRenderer
文章目录
- 杂项
-
- 行矢量,列矢量和矩阵
- view矩阵
- projection矩阵
- 齐次坐标
- 法线矩阵
- 各坐标系
- 绘制(线段、光栅化)
-
- 线框绘制
- 线段光栅化算法(直线光栅化)
- 光栅化
-
- 1) Edge Walk(扫描线算法)
- 2) Edge Equation(边界盒算法)
- 透明物体渲染
- 光线追踪
-
- 光线追踪与光栅化
- 基本步骤
-
- 生成相机-像素射线
- 射线与三角形求交
- 重心坐标插值计算其他信息
- 继续生成射线并递归
- 光照
-
- 着色
-
- 1) Gouraud Shading(高洛德着色)
-
- 定向光实现(高洛德着色)
- 点光源实现(Point)
- 聚光源实现(类似手电筒)
- 多光源
- 2) Phong Shading(冯氏着色)
- 阴影
-
- 软阴影
-
- · PCF
- · VSM
- · PCSS
- · DFSS
- 法线贴图
- 视差映射(Parallax Mapping)
- 全局光照
-
- 环境光遮蔽(AO)
-
- AO算法
- 间接光照
-
- RSM
- LPV
- VXGI
- SSDO
- SSR
- Gamma校正
- 纹理
-
- 纹理采样
- 纹理光照
- Mipmap
- 优化
-
- 背面剔除
- 透视修正
- 水平裁剪,垂直裁剪
- 抗锯齿
- 双线性滤波 / 三线性滤波 / 各种滤波
-
- 双线性滤波
- 三线性滤波
- 各向异性过滤
- 延迟着色(Deferred Shading)
- 空间划分算法
- Z-test,Early-z和Pre-z
- 反向z(reserved-z)
- 欧拉角、四元数
- 外部模型导入
杂项
行矢量,列矢量和矩阵
当使用列矢量时,矩阵对矢量进行的变换按从右往左的顺序阅读。使用行矢量时,顺序就变成从左往右了。(想象对结果进行转置,再把表达式代入这个转置,就能从列矢量得到行矢量了)

view矩阵
使用相机的look_at()来生成view矩阵时,up矢量写成 {0,1,0,1} 就可以生成标准左/右手系了,被mini3d那个项目的 {0,0,1,1} up矢量坑了好久才发现…
试验很久都不是标准左右手系,然后去排查行列矢量的使用,model矩阵,向量和矩阵乘法,perspective透视生成,屏幕坐标生成,frame_buffer问题,找了很久才发现是世界up矢量的问题
projection矩阵
这里讲得挺清楚:https://zhuanlan.zhihu.com/p/74510058
一直搞不清最后的w值是干嘛用的,查了很多资料终于知道了。w值就是储存的原z值。
把视锥体内点的 x , y 的范围分别映射到[-1,1];z 范围映射到[0,1]。注意,这是w=1时的情况。一般会把分量全乘z值,最后x,y就在[-w,w],z在[0,w]间(这里的w是乘z以后的w,即z值)。
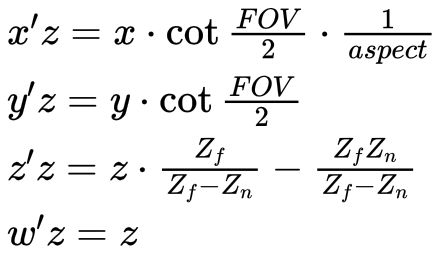
透视投影后,z值相较于观察坐标,会距离自己更远。(除了远近平面,这两个位置的z值不变)。参考
若近平面太近,会导致大多数z值靠后,精度低。
齐次坐标
用N+1维来表示N维矢量(x,y,z,w)。渲染中一般把w设置为1,方便运算。平移必须用多一维的矩阵,所以齐次坐标很容易表示坐标的变换。
w在透视投影时的几何意义是摄像机到近平面的距离。
法线矩阵
渲染管线中的法线变换矩阵
法线变换、逆转置、伴随转置
当进行MVP变换时,顶点坐标会变换,此时法线是不能跟随着乘MVP矩阵来变换的。法线和顶点坐标一同变换,变换后法线可能不垂直于顶点(物体发生不均匀缩放时)。
此时需要一个变换后法线仍垂直于顶点的方法,我们用法线矩阵来表示,法线×法线矩阵 后,法线矩阵代替原矩阵,法线可以和顶点一同变换,并且垂直于顶点。
利用法线和切线向量永远垂直,经过推导可以得出:法线矩阵 = (顶点变换的逆矩阵)的转置矩阵。若顶点变换到世界坐标(Model矩阵),则法线矩阵 = (M-1)T。
可以用 伴随矩阵的转置 = (M*)T 作为法线矩阵。(一个方阵的逆阵是该方阵的伴随矩阵除以该方阵的行列式。即伴随矩阵和逆矩阵只差一个系数(即只影响变换后法线的长度),而伴随矩阵总是存在的,所以我们可以用伴随矩阵的转置来作为法线变换矩阵。注意变换得到的新法线不一定是单位长度的,需要进行归一化。)
逆转置和伴随转置: 某些变换可能没有逆矩阵(当矩阵的秩减少时,如z值缩放为0,无法求逆),但矩阵都有伴随矩阵,所以伴随转置矩阵作为法线矩阵是更通用的选择(但伴随矩阵可能求解更慢)。
各坐标系
局部坐标(模型坐标)和世界坐标很好理解,不再赘述。
观察坐标: 在世界坐标中,所有点随摄像机移动,移动方式为:摄像机经过平移移动到原点处,且旋转至up向量与设置的up向量(一般为世界up向量)一致。

投影坐标、NDC坐标: 在观察空间中抽象出平截头体,将所有点变化到近远平面之间(即平截头体中),变换到投影坐标。变换完后,w存入了原z值,这时再进行透视除法(所有分量同时除以w)(实际上透视除法才是投影的操作),变换到NDC坐标,即透视投影矩阵和透视除法是分开的。
透视投影之后,透视除法之前,x、y、z范围为:
− w ≤ x ≤ w {-w \leq x \leq w} −w≤x≤w
− w ≤ y ≤ w {-w \leq y \leq w} −w≤y≤w
0 ≤ z ≤ w {0 \leq z \leq w} 0≤z≤w
透视除法之后,x、y、z范围为:
− 1 ≤ x ≤ 1 {-1 \leq x \leq 1} −1≤x≤1
− 1 ≤ y ≤ 1 {-1 \leq y \leq 1} −1≤y≤1
0 ≤ z ≤ 1 {0 \leq z \leq 1} 0≤z≤1

绘制(线段、光栅化)
线框绘制
就是绘制线段。
线段光栅化算法(直线光栅化)
绘制直线的光栅化算法
因为搜索三角形光栅化相关算法的时候看到了直线的光栅化,就进一步了解一下。
有三种基本算法:数值微分DDA(Digital Differential Analyzer)算法,中点画线算法,Bresenham算法。
DDA很简单,就是直线方程稍微推导下,然后Bresenham是DDA和中点画线的优点结合,所以我的软渲染也采用的Bresenham算法光栅化直线。
光栅化
相关介绍
参考:
三角形光栅化
光栅化填充三角形算法
How to determine if a point is in a 2D triangle?
三角形光栅化时遇到的坑
一般有两大类:Edge Walk和Edge Equation。
为了好理解,可以把Edge Walk叫扫描线算法(SCANLINE),Edge Equation叫边界盒(BOUNDINGBOX)算法(我自己的叫法…)。
1) Edge Walk(扫描线算法)
思想是画三角形的左右两条边,当y值相同时就水平画一条线来填充三角形。计算比较复杂,适合cpu,cpu上一般比Edge Equation快。
在Nanite的研究中,表明当三角形很小时(左右长度小于4个像素),Edge Equation会比Edge Walk快。
Nanite论文
1.经典算法(Standard Algorithm)(有缺陷 --> 已解决)
经典算法拼接处有毛刺和拼接不齐问题

毛刺问题是当y的小数部分舍去的时候,如果斜率特别小,y变化一点点就会导致x变化特别大,然后就导致了x方向突增或突减。
解决:将所有逻辑改为向上取整,即可解决此问题。因为向上取整会保证所有坐标点都会落在原始三角形内,而向下取整会导致某些不在三角形内部。

拼接不齐 问题是最开始取y值的时候,y值的小数点部分舍去会导致x出现偏差,需要根据y值的变化去修正x。
解决:
xleft = x0 +(ceil(y0) - y0) * xleft_step;
xright = x1 + (ceil(y0) - y0) * xright_step;
2.BresenhamAlgorithm
和线段的Bresenham算法差不多,但是是同时画两条线,三角形左边和右边,假定左边先画,且从上到下画,当左边的y增加1时,要暂停等右边的y也到这里,然后左y=右y时,在该y坐标画一条x1到x2的直线。
目前试验该算法不会有拼接不齐问题,毛刺现象极少发生,可暂时忽略。
用Bresenham算法来绘制三角形不太好进行颜色的线性插值。
2) Edge Equation(边界盒算法)
这个的思想是先计算出三角形的包围盒(把三角形包住的矩形),然后遍历包围盒中的每个像素点,判断是否在三角形内,如果在内部就着色。
边界盒着色比较精准,但是一般比扫描线算法慢。
Edge Equation的插值可以用三角形重心插值。
透明物体渲染
在z-buffer引入前,光栅化通常都是用画家算法,即对每个物体排序,再从后往前绘制。引入z-buffer后,不透明物体渲染可以顺利解决了,但是半透明物体不行。
实现 透明度(Transparency) 的技术通常为 混合(Blending) ,混合的最终效果和次序有关(混合时,需要把前面步骤计算得到的颜色当作整体,再乘混合因子,显然次序改变后结果不同)。所以渲染透明物体的做法之一就是对透明物体从后往前绘制,这是次序有关的半透明混合。
对透明物体排序开销较大,而且物体粒度太大,不易处理。所以需要次序无关的半透明(Order Independent Transparency,OIT) 。
次序无关的半透明处理常用算法:Depth Peeling(深度剥离),Per-Pixel Linked Lists OIT(逐像素链表),Adaptive Transparency(自适应透明度),Screen-Door transparency(纱门透明度),Weighted Average(加权平均值算法)。
Depth Peeling(深度剥离): 每次找出从视点出发,没处理过的最前面一层的半透明图层,然后记录,并标记为处理过,最终到达预设的N层或者剥离完为止。最后把每层的颜色混合起来。
Depth Peeling 是一种很慢,非常费显存空间(空间分配可确定),但对硬件没什么高要求的 OIT 方法。
Per-Pixel Linked Lists OIT(逐像素链表): 为每个像素开一个链表,每次遇到这个像素有半透明片段就把该半透明相关信息插入该链表。最后将链表中的内容排序,再混合。
速度比 Depth Peeling 快了很多,显存空间也比 Depth Peeling 更加节省,但节点纹理具体需要多大无法事先做准确的预估,因此显存的具体消耗不可控。
Adaptive Transparency(自适应透明度): 是对Per-Pixel Linked Lists OIT的优化,它将经典混合公式进行了修改,引入了一个能见度函数,修改后的混合公式最终结果与次序无关。完美的做法是遍历链表来建立能见度函数,但这样就和原本的逐像素链表一样了。一个很好的思路是将能见度函数近似的表示为一个单调递减的定长数组,这样就做到了优化。当然,简化了混合计算复杂度,但也因此丢失了混合精度。
Screen-Door transparency(纱门透明度): 将alpha值换成mask来决定像素是否写入颜色缓冲区。例如:alpha为0.5时,mask值为0.5也就是说绘制时有一般像素会被绘制另一半不会绘制,alpha越小被绘制的像素越少。缺点很明显,像素感较强,不过有时也可满足特定目标。
Weighted Average(加权平均值算法): 对于某个位置的像素点,如果所有的半透明物件是相同的颜色,那么渲染的结果与它们的渲染顺序无关。那么,对于不相同颜色值的情况,用某一个颜色来替换这些颜色,比如这些颜色的平均值。对于这种情况,我们使用各个颜色的不透明度作为权重来计算出它们的平均值。
此算法的优点很明显,效率高,速度快,只需要对物体进行一次的渲染,然后加上一次全屏的后处理。但是缺点也是同样的明显,透明结果只是一个近似值,而不是确切的正确结果。
参考:https://zhuanlan.zhihu.com/p/353940259
https://www.zhihu.com/question/382932468/answer/1111595945
Screen-Door transparency(纱门透明度)
光线追踪
效果:
 光栅化(无阴影) |
 光追(Whitted-Style) |
 光追(Whitted-Style),添加全局光照Trick(右侧方块有部分蓝色反光) |
 光追(PBR),4深度,4采样点 |
 光追(PBR),16深度,2048采样点 |
参考:
smallpt: Global Illumination in 99 lines of C++
GAMES101 (光线追踪教程)
Ray Tracing: Rendering a Triangle (计算射线与三角形相交)
Ray-Tracing: Generating Camera Rays (生成相机到屏幕射线)
Invert 4x4 matrix (计算4x4矩阵的逆矩阵)
Random float number generation (生成[l,r)的随机数)
光线追踪与光栅化
光栅化(Rasterize): 先回顾光栅化,我们是把三角形的坐标经过MVP变换,最终确定三角形的某部分对应屏幕的某个像素,然后计算这个部分的颜色(比如光照等),最后得到这个像素的颜色值。
光线追踪(Ray Tracing): 是把光栅化过程反过来。我们把坐标统一到世界坐标,确定好观察位置(摄像机位置),然后把屏幕上每个像素的坐标变换到世界坐标(后面会介绍如何变换)。现在,得到相机位置和像素位置,我们可以求出以相机为起点,相机到像素的向量为方向的一条射线。这条射线其实就是光线传播的逆过程。我们将射线弹射多次后,就可以确定像素的颜色。
基本步骤
这里是最基本的步骤,不涉及加速结构、光照计算方式等探讨。
1.遍历屏幕像素,为每个像素生成相机-像素射线,并进行后续计算。
2.储存所有物体的三角形片元,每次射线与所有三角形求交,以计算交点。
3.计算出交点后,可以采用重心插值,计算出该点的其他信息。
4.采用递归,以交点为起点,继续生成射线在场景中追踪,最后确定出起点像素的颜色。当然应该设定最大递归深度。
生成相机-像素射线
Ray-Tracing: Generating Camera Rays (生成相机到屏幕射线)
仿照MVP矩阵的思路,比较容易得出像素在观察空间中的坐标(其实也没那么容易,可以看上面的参考)。具体是 像素真实坐标 -> NDC(Normalized Device Coordinates)坐标 -> 透视裁剪坐标 -> 观察坐标。
得出像素在观察空间的坐标后,只需要把该坐标乘上MVP矩阵里V矩阵的逆矩阵(观察矩阵),就可以把坐标从观察空间转变为世界空间了。相机的世界坐标是已定义的,可以直接得出射线。
参考:Invert 4x4 matrix (计算4x4矩阵的逆矩阵)
当然,有时射线的生成需要一些随机性(真实世界有无数光线,不能模拟无数光线,只能模拟一定数量的随机光线了)。我们一般在像素真实坐标时,引入随机偏移(遍历像素时x递增1代表移动1个像素,此时让x偏移[0,1)就等于在这个像素中进行偏移)。
参考:Random float number generation (生成[l,r)的随机数)
注意射线的方向向量需要单位化(normalize),这样得出的参数t才有正确的几何意义。
射线与三角形求交
Ray Tracing: Rendering a Triangle (计算射线与三角形相交)
首先,肯定是储存所有的三角形片元。
生成射线后,遍历所有的三角形片元与该射线求交,得到最近的交点。射线与三角形求交有多种方法,这里使用Möller-Trumbore algorithm。
注意得出参数t值后,需要判断 t>0.0f ,以保证交点在射线前方。
若没有任何在射线前方的交点,退出递归。
重心坐标插值计算其他信息
这部分和Phong Shading一样。需要插值计算交点的颜色、法线等信息。
当然,对于不同的着色方法,部分信息用插值计算会出现不太正确的结果。比如法线,我们有时应该用面法线(PBR中),而不是顶点的插值法线。
继续生成射线并递归
现实中的光线会弹射无限次,我们在光线追踪中,也需要不断弹射射线。
弹射的射线就是以交点为起点,某一方向为方向向量的射线。方向向量的确定随光线追踪方式不同而改变(比如镜面是完全反射,漫反射是随机方向,折射是和折射率有关,等等)。
确定一个最大递归深度,达到深度后一般会返回黑色({0,0,0})。
递归结束后颜色如何累加,也随具体实现方式不同而变化。
光照
着色
1) Gouraud Shading(高洛德着色)
(无光照的高洛德着色↑)
高洛德着色基本就是算出各个顶点的颜色,然后光栅化时按顶点颜色来插值。
在光栅化扫描线经典算法的基础上完善高氏着色(Gouraud Shading) (用BresenhamAlgorithm光栅化来完善高氏着色很不好写,很繁琐)。
注意颜色插值在经典算法里也同样有拼接不齐之类的问题,需要修正。而且注意能用原始float数据就不要换成int截取的数据,容易出问题(被坑了很久)。
目前发现颜色有需要透视修正的问题。(已解决)
定向光实现(高洛德着色)
学了下OpenGL的光照部分,对光照有了初步理解,开始写一个最简单的平行光照+环境光+漫反射。
参考:
LearnOpenGL:基础光照
(前方白色矩形为光源。对光源使用了另外的着色器,以保证光源为常亮白色)
实现:
光照主要是光源的位置,环境光照,漫反射光照,镜面反射光照,光源的颜色一般就包含在环境光和漫反射光部分了。为啥一个光源有这些定义?因为光对材质的影响主要就是这些,为了方便光照处理时和材质的相关计算,就这么定义了。
平行光源就没有光衰减什么的了,所以很简单,先实现它。
目前也没有定义材质,是从顶点的颜色来处理的。
具体方法: 因为光照需要z轴信息,所以当顶点映射到世界或者观察坐标再处理光照均可,这里选择在世界坐标处理顶点(更直观)。处理时按照相关公式对顶点颜色进行更改即可。
因为是高洛德(Gouraud)着色,所以是对顶点进行光照处理后,再线性插值。高洛德(Gouraud)着色在镜面光照部分的处理明显不如冯氏(Phong)着色。
环境光实现如下:
color_t ambient1 = light->ambient * v1.color;
color_t ambient2 = light->ambient * v2.color;
color_t ambient3 = light->ambient * v3.color;
//v1,v2,v3为三角形的三个顶点
漫反射稍微复杂些:(漫反射光照计算相关资料可以去刚刚的参考看)
// 使用兰伯特余弦定律(Lambert' cosine law)计算漫反射
vector_t norm = vector_normalize(v_normal); //顶点所在平面的法向量,先给单位化一下
vector_t light_dir1, light_dir2, light_dir3;//从平面指向光
float diff;
light_dir1 = vector_normalize(-light->direction);//平行光
light_dir3 = light_dir2 = light_dir1;
diff = max(vector_dot(norm, light_dir1), 0.0f);
color_t diffuse1 = light->diffuse * diff * v1_tmp.color;
diff = max(vector_dot(norm, light_dir2), 0.0f);
color_t diffuse2 = light->diffuse * diff * v2_tmp.color;
diff = max(vector_dot(norm, light_dir3), 0.0f);
color_t diffuse3 = light->diffuse * diff * v3_tmp.color;
镜面反射光照:
vector_t reflect_dir1, reflect_dir2, reflect_dir3;
vector_t view_dir1, view_dir2, view_dir3;
reflect_dir1 = vector_normalize(vector_reflect(-light_dir1, norm));//reflect计算反射光
reflect_dir2 = vector_normalize(vector_reflect(-light_dir2, norm));
reflect_dir3 = vector_normalize(vector_reflect(-light_dir3, norm));
view_dir1 = vector_normalize(camera->pos - p1);
view_dir2 = vector_normalize(camera->pos - p2);
view_dir3 = vector_normalize(camera->pos - p3);
float shininess = 32.0f;
float spec = pow(max(vector_dot(view_dir1, reflect_dir1), 0.0), shininess);
color_t specular1 = light->specular * spec * v1_tmp.color;
spec = pow(max(vector_dot(view_dir2, reflect_dir2), 0.0), shininess);
color_t specular2 = light->specular * spec * v2_tmp.color;
spec = pow(max(vector_dot(view_dir3, reflect_dir3), 0.0), shininess);
color_t specular3 = light->specular * spec * v3_tmp.color;
添加光照处理后透视修正会失效,尚不清楚原因。
注意这些光照处理都是在世界坐标进行的,观察坐标也可以光照处理,但相关方程需要变化。
点光源实现(Point)
效果:

点光源和定向光源主要的区别:1.光的方向不是平行的;2.光会衰减。
漫反射的光照修改:(当然对应的镜面光照要使用的 light_dir 也更改了)
light_dir1 = vector_normalize(light->pos - p1);
light_dir2 = vector_normalize(light->pos - p2);
light_dir3 = vector_normalize(light->pos - p3);
衰减计算:(用衰减公式)
//这里只写对一个顶点的处理,其他两个顶点类似
float distance1 = vector_length(light->pos - p1);
float attenuation1 = 1.0 / (light->constant + light->linear * distance1 +
light->quadratic * (distance1 * distance1));
v1_tmp.color = (ambient1 + diffuse1 + specular1) * attenuation1;
聚光源实现(类似手电筒)
效果:
聚光源原理也不阐述了,之前的链接里讲了。
聚光源的衰减可以用点光源的衰减,然后和点光源的区别:有一个切光角(Cutoff Angle),在切光角外的部分几乎没有光。
所以我们需要 点到光源的方向向量和光源方向向量的夹角 的相关信息,来判断这个点是否在切光角内。
然后再加个外切光角,来平滑边缘。
float epsilon = light->cut_off - light->outer_cut_off;
float theta1, theta2, theta3;
float intensity1, intensity2, intensity3;
vector_t light_direction = vector_normalize(-light->direction);
theta1 = vector_dot(light_dir1, light_direction);
intensity1 = CMID((theta1 - light->outer_cut_off) / epsilon, 0.0, 1.0);
diffuse1 *= intensity1; specular1 *= intensity1;
//另外两个顶点类似
目前发现在距离一个平面特别近时,聚光会反而变暗消失。猜测是因为高洛德着色对顶点处理,而距离平面特别近时,顶点和摄像机的夹角特别大,在切光角外面去了,所以变暗。
多光源
不是全局光照,没有考虑反射折射那些,就是单纯的多个光源效果叠加。颜色相加,比较简单。
效果:
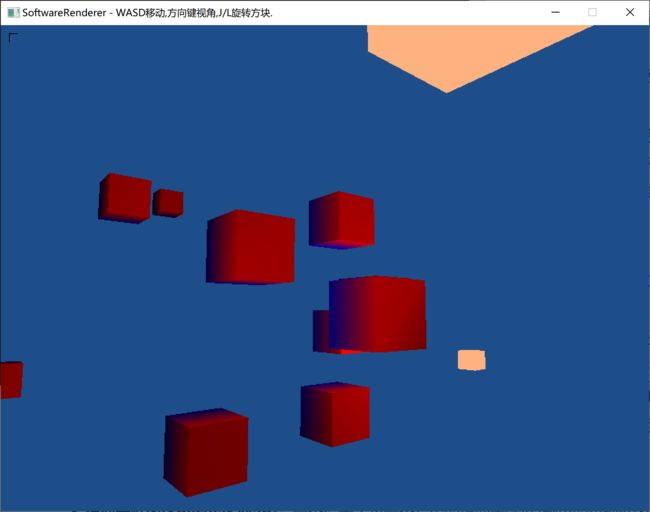
(图中右上角大的定向光,下方点光源,摄像机位置有朝前的聚光源)
2) Phong Shading(冯氏着色)
重心坐标计算
表面法向量插值
重心坐标插值
重心坐标插值的透视修正
冯氏着色比高洛德着色真实,但效率低一些。
冯氏着色和高洛德着色的区别:
高洛德着色:对三角形顶点进行光照计算,算出三角形顶点的颜色后,在光栅化时插值计算颜色。
冯氏着色:对三角形的世界坐标、法线和每个像素点的颜色进行插值,然后再用每个像素的信息去计算光照。显然,每个像素都进行光照计算,会慢很多。
每个像素的世界坐标、法线、颜色: 从阴影这部分可以得到世界坐标插值的结果(因为阴影需要用到世界坐标),拿到世界坐标后,可以用重心坐标插值,用重心坐标的系数得出每个像素法线和颜色的插值结果。这里要注意透视修正。
坑点比较多,可以详细看代码:
//这里最初所有数据都是进行了透视修正的,所以后面会看到 *wi 这个计算
vertex_t v;
v.pos = { world_xi , world_yi , world_zi , 1 };//这里不乘wi,因为后面会乘wi
barycentric_t bary = Get_Barycentric(v.pos, extra_data.world_pos.p1, extra_data.world_pos.p2, extra_data.world_pos.p3);//计算重心坐标系数
v.color = top.color * wi * bary.w1 + left.color * wi * bary.w2 + right.color * wi * bary.w3;
v.normal = top.normal * wi * bary.w1 + left.normal * wi * bary.w2 + right.normal * wi * bary.w3;
v.pos = v.pos * wi;//转换回世界坐标,这样光照计算才是正确的
Phong_Shading(v);
color_use = v.color;
效果:
左: 高洛德着色, 右: 冯氏着色 (GIF左侧是帧率,很明显冯氏着色慢一些)
阴影
效果:
(下图是高洛德着色下的实现,因为高洛德不好处理每个片元,所以简单地让颜色*=0.5来变暗,不够真实)
(下图是基于冯氏着色实现的,真实很多)
软件渲染时期,是计算顶点经过光源投影后的位置(也就是连接顶点和光源,生成一条直线,再看这条直线和哪些平面相交),顶点数选取可自己确定,顶点越多,阴影形状越真实。
硬件渲染不能用这么麻烦的计算了,所用技术有阴影贴图(Shadow Mapping)、阴影体积(Shadow Volume)。
下面介绍阴影贴图(Shadow Mapping)的做法(效果图的实现方法也是阴影贴图)。
步骤如下:
1.以光源为视角渲染场景,记录z-buffer里的值,把这个值存到一个贴图里,这个贴图就是阴影贴图。
2.以正常视角渲染场景,但此时需要知道每个点对应的光源空间中的坐标,将点变换到光空间后,记录这个点此时的z值Current Depth,再对阴影贴图进行采样得到Shadow Depth,如果Current Depth > Shadow Depth,说明该点在阴影中,此时标记一下,再在正常视角中处理阴影。
步骤2这里有一些不太好处理的地方:
- 正常视角渲染时,怎么得到像素在光空间中的坐标?
一种容易想到的是直接把光栅化时的坐标乘上正常渲染的观察矩阵和透视矩阵的逆矩阵,变回世界坐标,再乘光源的变化矩阵。但是逆矩阵求解其实是很慢而且不够精确的。我们这样解决:顶点变化到世界坐标以后,记录下来,光栅化时再对世界坐标插值计算新的{x,y,z},最后将得到的坐标变化到光源空间。注意,插值计算世界坐标时也要透视修正。 - 读取ShadowMap时,应该从插值得到的世界坐标变化到光源坐标系下的屏幕空间,再在这个屏幕空间中取对应点的ShadowMap值,这样才能得到正确结果。
问题: 若阴影贴图精度不够,会出现阴影失真(Shadow Acne),悬浮(Peter Panning),锯齿(对应的解决方案叫 PCF(percentage-closer filtering) ) 等问题。
阴影失真(Shadow Acne): 阴影贴图的一个不在阴影中的采样点可能对应了好几个像素,在计算这些像素的时候,可能有的小于贴图的深度,有的大于,于是就会出现交错阴影的现象,本来应该是都被点亮的。可以采用增加阴影偏移(shadow bias) 或者 生成阴影贴图时采用物体背面计算深度(正面剔除(front face culling))来解决。
阴影偏移(shadow bias): 该被点亮的地方被计算得大于贴图的深度值了,所以可以把计算出的Current Depth整体减小(即减去一个偏移量),这样可以避免部分失真。当偏移量不够时,仍有失真。加上偏移量后,会出现 悬浮(Peter Panning) 问题。
悬浮(Peter Panning): 原本在遮挡物与阴影接触的地方,深度差值就很小,加上偏移量后可能在这些边缘应该处于阴影的地方,被点亮了,看起来就像阴影悬浮。
正面剔除(front face culling)解决阴影失真: 比加偏移量好的地方是不会出现悬浮。生成阴影贴图的时候采用背面的深度值,这样在正常渲染的时候,正面的深度值肯定小于背面,所以不会出现某些应该被点亮的地方却计算出在阴影中的情况了。
PCF(percentage-closer filtering): 就是阴影的抗锯齿滤波,和一般贴图在边缘的抗锯齿差不多。PCF时,每次阴影贴图的采样是对周围几个点采样,而不是只采样当前点,最后再平均一下可见性。
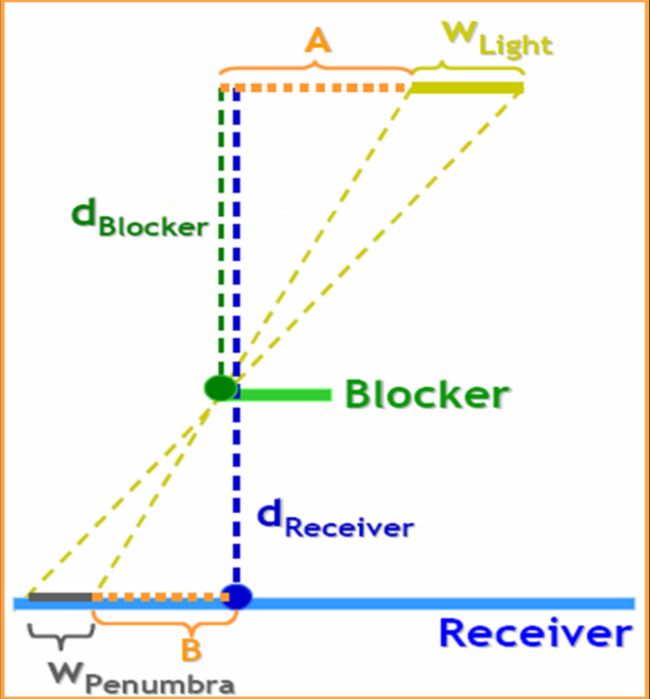
软阴影
参考:GAMES202
实时渲染中的软阴影技术
软阴影: 现实中的光源都是有体积的,不是完美的点光源,所以会有部分阴影没有那么黑。具体现象就是从阴影到光亮部分有一个缓慢过渡。
中心实现思想: 软阴影的生成中心思路就是求出一个像素周围有多少部分处于阴影中,再来确定该像素没被照亮的比例。
常见实现: PCF(Percentage-Closer Filter)、CSM(Convolution Shadow Maps)、VSM(Variance Shadow Mapping)、ESM(Exponential Shadow Mapping)、MSM(Moment Shadow Mapping)、PCSS(Percentage-Closer Soft Shadows)、DFSS(Distance Field Soft Shadows)。
PCF、CSM、VSM、ESM、MSM都是生成一致性软阴影的,PCSS解决的是不同的问题(生成不一致的软阴影),一般和前面的算法结合使用。
DFSS是比较新的技术,不使用Shadow Mapping。
· PCF
显然,PCF会对一个像素取ShadowMap上周围的点来确定遮盖度,这样就可以生成软阴影。缺点也很明显,需要多次采样,效率低。
· VSM
方差阴影贴图。应用了正态分布、切比雪夫不等式等技巧。
回想中心实现思想,其实我们只需要知道一个像素及其周围,处于阴影中的部分占据的比例是多少。比如取了周围9×9的范围,有30%处于阴影中,那么我们就该应用30%的阴影效果(其实和PCF一样)。
VSM对PCF的优化: PCF多次采样很慢,VSM就是解决多次采样慢的问题。VSM通过一些公式推导,用一个等式就可近似算出处于阴影中的比例。
VSM是把周围处于阴影中的分布近似为一个正态分布(或高斯分布)。当然这种近似是不完全正确的。当作正态分布以后,我们只需要知道这个分布的均值和方差,再利用切比雪夫不等式来近似,就可以直接得出处于阴影的比例。
均值: 可以用MipMap或者SAT(二维前缀和实现),快速求出某一区域的总和。均值可以从总和得到。MipMap不如SAT精确。
方差: 方差Var(X)=E(X2)-E2(X)。E期望就是均值。所以,只需要在生成阴影贴图时,同时储存深度值的平方。平方值一般放在RGBA的G通道上(深度放在R通道)。
求出了均值和方差,再根据切比雪夫不等式进行近似,就可以得到阴影占比了。
VSM有许多地方是近似。近似认为周围是正态分布,MipMap的均值近似,对切比雪夫不等式近似。这些近似会导致一些问题。比如若周围不是正态分布,就会出现漏光现象。
· PCSS
Percentage-Closer Soft Shadows。软阴影在边界上软的程度是不一样的(越靠近边缘越软),PCSS就是解决这个问题的。
不使用PCSS时,我们对一个像素周围的采样大小是固定的,这就会导致软阴影是一致的。PCSS可以控制采样搜索范围。
首先,当光源有体积时,才会出现软阴影。有遮挡物,才会有阴影。
PCSS主要有三步: 1.确定遮挡物的平均深度。2.确定采样范围。3.以采样范围来生成软阴影(PCF、VSM等)。
1.确定遮挡物平均深度。对阴影贴图的一定范围采样即可,这里也可以用一些近似来避免多次采样。
3.生成软阴影。和PCF之类的步骤一样,只不过采样范围变了。
· DFSS
参考:GAMES202-P5
Distance Field Soft Shadows,距离场软阴影。比较新的技术,相对于前面的算法,思路是比较独立的。使用了Signed Distance Functions来生成距离场,并根据距离场来生成不一致的软阴影。
该技术没有使用Shadow Mapping,而是用距离场来取代。每次渲染前将距离场预先生成好(距离场只需要在有物体运动时或非刚体形变时才需要完全重新生成),然后根据储存的距离场采样计算出非一致软阴影。
距离场需要三维的,所以所需的内存比ShadowMap大很多。但是距离场在某些情况下不用每帧都重新生成,所以比ShadowMapping更快。
对比PCSS,DFSS速度更快、质量更高。但需要预计算、需要大储存空间、和PCSS一样会有一些不精确的地方。
法线贴图
参考:LearnOpenGL
法线贴图: 对贴图应用光照最直接的是把整个贴图当作平面,但是如果贴图上有一些坑坑洼洼的地方,这时光照的效果就不够真实。法线贴图就是和贴图附加在一起,标明每个纹素对应的法线。有法线了,光照效果会真实很多。
世界坐标下法线贴图的不正确: 法线贴图的法线方向一般都是相对于贴图的坐标的,假定贴图正对视线,以世界坐标为基准,那么贴图的坐标就是z轴朝外(世界坐标的z轴),法线也z轴朝外。但是当贴图放平时,贴图的法线变成y轴朝上了,但法线贴图还是z轴朝外,结果显然不正确。
切线空间: 我们把法线贴图总是基于贴图的正z轴方向的空间定义为切线空间。为了解决上述问题,我们可以想到,应定义一个转换矩阵,可以让法线贴图从切线空间转换到世界坐标时与贴图能正确对应,或者用这个矩阵把需要的信息(光源方向、视线方向)变化到切线空间中去。这个矩阵就叫TBN矩阵(tangent、bitangent和normal)。
切线空间坐标轴: 一般切线对应贴图的u,副切线对应v。
使用切线空间原因: 基于模型坐标系的法线贴图,在换到不同的模型下时候法线贴图不能复用。
引入切线空间让法线贴图可以在相同网格形状模型(或许是子模型)但不同模型坐标系的多个模型间可以共享法线贴图。
切线空间使用场景: 当需要三角形的xy与贴图的uv对应时(或者三角形的z和法线贴图的z),就可以使用切线空间。
TBN矩阵:
可以把切线坐标的向量转换到世界坐标。或者求TBN的逆矩阵,可以把世界坐标转换到切线坐标(这里也可以用TBN的转置矩阵当作逆矩阵,因为TBN矩阵是正交且单位化的,这种矩阵的转置即等于逆)。
TBN矩阵求解推导
TBN矩阵的求解方法如下:
//假设平面使用下面的向量建立起来(1、2、3和1、3、4,它们是两个三角形)
// positions
glm::vec3 pos1(-1.0, 1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3(1.0, -1.0, 0.0);
glm::vec3 pos4(1.0, 1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// 贴图当前在世界坐标的法线方向
glm::vec3 nm(0.0, 0.0, 1.0);
//第一个三角形的TB向量计算(点1、2、3), 第二个类似
glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;
GLfloat f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);//实际上这里可以直接用T向量和N向量叉乘得到
有了TBN矩阵,仿照MVP矩阵的使用,很容易就能正确应用法线贴图了。
视差映射(Parallax Mapping)
视差问题: 法线贴图可以纠正光照结果,但凹凸不平的高度不止影响光照,也影响视线观察到的位置。对纹理的具体体现就是采样时坐标不应该直接对应,应该有一点点偏移。
视差映射: 我们要确定这个采样偏移量,所用的方法就是视差映射(或者叫视差贴图,但是概念上其实计算采样偏移量只需要一个高度贴图,后面的计算应该叫视差映射)。
高度/深度贴图: 视口变换后的z值在一个范围内(OpenGL是[0,1]),可以将z值减去1,得到所有值均<=0的深度贴图(当作高度贴图用)。然后依据这个贴图来进行视差映射。
注意,视差映射的计算也和法线贴图一样,需要考虑切线空间。
假设已经得到TBN矩阵了,最简单的视差映射的步骤大致如下:
//顶点着色器
vs_out.TangentLightPos = TBN * lightPos;
vs_out.TangentViewPos = TBN * viewPos;
vs_out.TangentFragPos = TBN * vs_out.FragPos;
//片元着色器
vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir);
if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0) {discard;}
//对不同的视差映射方法, 下面的函数应该有所不同
vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{
float height = texture(depthMap, texCoords).r; //depthMap, 深度贴图
vec2 p = viewDir.xy / viewDir.z * (height * height_scale);
return texCoords - p;
}
全局光照
环境光遮蔽(AO)
环境光遮蔽(Ambient Occlusion): 简称AO。环境光遮蔽是模拟全局光照的阴影效果。比如在一个花盆底部,因为被遮盖了,其实是没有什么光照能照到那些位置的,此时应该有阴影,但传统的光照模型有一个固定的环境光分量,场景里所有像素都会受到环境光的影响,显然是不正确的。
光线追踪(Ray Tracing): 提到AO就肯定少不了光追,传统的AO一般是在屏幕空间进行的,而屏幕空间的遮蔽信息和真实情况可以有很大区别。用光追来计算AO会准确很多。这里不做展开。
参考:游戏里的光线追踪和以前的环境光遮蔽有什么联系和区别
AO算法
参考:游戏中的全局光照(三) 环境光遮蔽/AO
What Is Ambient Occlusion? (SSAO, HBAO, HDAO And VXAO)
Ambient Occlusion(AO)使用指南
有SSAO、HBAO、HDAO、GTAO、VXAO等。
SSAO: Screen-Space Ambient Occlusion。可以说是AO的起源,比较简单。
算法大致是在每个像素周围生成一个球体(或半球体),再在球体内随机采样,看采样点是否位于其他物体内部,在其他物体内部的采样点越多,说明这个像素被遮盖得越多。
步骤如下:
1.用类似延迟渲染的技术,储存需要的逐片段信息(位置、法线、颜色,采样核心)。
2.使用采样核心中的采样点采样,再与z缓冲对比深度,算出AO值。
3.进行优化。一是考虑边缘平滑。二是因为随机采样,会有噪点,最好进行模糊处理消除噪点。
HBAO: Image-space horizon-based ambient occlusion。效果比SSAO稍微好一些,是基于物理效果的,由英伟达提出,硬件支持。
大致步骤是:在每个像素周围确定一个一定大小的球体,算出高度比像素点最高的一个点,再根据像素点的面法线算出像素点切线,最后比对一下切线和最高点的Sin值。
参考:HBAO(屏幕空间的环境光遮蔽)
HBAO+: SSAO和HBAO的改进。若角色远离了墙面,在屏幕空间中是看不出来的,就会造成角色边缘生成错误的AO。HBAD+采用两个Pass来处理。
参考:Unreal | SSAO的升级HBAO+
HDAO: High Definition Ambient Occlusion。和HBAO原理差不多,只不过是AMD实现的。
GTAO: Ground Truth Ambient Occlusion。对HBAO的改进。
参考:UE4 Mobile GTAO 实现(HBAO续)
VXAO: Voxel Ambient Occlusion。很新的技术。把屏幕空间的2D像素转化为3D的体素了。效果几乎和光追一样。
间接光照
GAMES202 Global Illumination
非全局光照就是只考虑光源直接照射,全局光照是考虑光的反射等。光栅化的全局光照一般指光从光源打到反射面(直接光照),再从反射点反射一次(间接光照),多次反射开销太大。
基本思路: 把直接光照照到的地方当作新光源(次级光源)。
算法: RSM(Reflective Shadow Maps),LPV(Light Propagation Volumes),VXGI(Voxel Global Illumination)。
RSM
Reflective Shadow Maps——GAMES202学习笔记
借助了Shadow Map的思路。显然,Shadow Map可以得到被直接照亮的部分,我们就可以很容易得到次级光源。
次级光源对全局光照的贡献一般用渲染方程来计算,那么我们就需要在Shadow Map中额外保存渲染方程会用到那些变量(世界空间坐标、法线、反射光通量等)。
RSM的近似假设:
1.所有反射面都是Diffuse的。如果用渲染方程来计算全局光照,最麻烦的是BRDF项。如果反射面不是Diffuse的,那每个着色点的BRDF就和光源到着色点的方向有关,开销很大。所以RSM假设所有反射面都是Diffuse的。
2.所有次级光源都是Visibility的。对于每个光源,需要一个ShadowMap才能知道可见性,明显开销太大了。
LPV
Light Propagation Volumes
光照传播体积。把场景划分成多个体素,计算每个体素的Radiance,之后对于每个着色点,直接取体素的信息就可以了。
步骤:
1.和RSM一样,用ShadowMap得到次级光源。
2.将空间划分成很多小格子(体素),把次级光源存入体素中,每个体素得到一个有各个方向的Radiance的和,这时可以用SH(球谐函数)来压缩所有Radiance的信息。
3.每个体素向周围传播,迭代多次,得到所有体素的Radiance。这里也是不考虑Visibility的。
总结: 把空间划分成多个体素,从次级光源开始,实时计算出所有体素的Radiance,就可以实现全局光照了。
因为用SH去储存每个体素的Radiance,所以基本只能表示Diffuse的反射面。
VXGI
Voxel Global Illumination 体素全局光照(二)
体素全局光照。把场景体素化,对于每个着色点,根据它表面的BRDF(所以不能用SH压缩,一般用储存各个直接光源的方向和表面法向量来计算BRDF),来追踪光线的传播,并计算追踪过程中碰到的体素的Radiance(BRDF或者其他方法来计算)。
和LPV很像,只不过LPV是从每个次级光源开始向周边扩散算出所有体素,而VXGI是从每个着色点类似光追来计算。
追踪光线的传播,对于Glossy表面,一般追踪一个锥形,对于Diffuse表面,追踪多个锥形(向各个方向都反射)。
SSDO
GAMES202 - P9
Screen Space Directional Occlusion。屏幕空间定向光遮蔽。
这种技术基本可以取代SSAO,它和SSAO的思路很像。
与SSAO区别: SSAO是默认有一个环境光,再根据计算去减少环境光。SSDO正好反过来,没有默认的环境光,环境光是靠直接光照的反射得到的。
思路: 和SSAO一样,屏幕空间中,在一个着色点周围半球采样,看采样点是否被遮盖(采样点深度更大),若被遮盖,说明这里可能有反射光反射到着色点。
对于一个着色点的一个采样点,就找到对应的遮盖点,再根据这个遮盖点的法线、颜色等信息,就可以得到其反射光对着色点的贡献了。
等于说采样点被遮盖时,SSAO减少环境光,而SSDO增加反射光(体现出来就像是环境光了)。
SSDO基本算是间接光照(RSM等)+全局光照阴影(类似AO)。
SSR
GAMES202 - P9
Screen Space Reflection。屏幕空间反射。
这个技术算是屏幕空间的光线追踪,因为放到屏幕空间了,所以实时渲染也基本可以接受。
思路: 在屏幕空间中,对于要计算反射的那些着色点,从摄像机发射一个射线过去,再根据BRDF看要怎么反射,最后根据反射光线在屏幕空间中采样(和光线追踪的思路差不多了)。这里有光线追踪,肯定也需要记录一些三维信息。
有很多优化技巧,比如用MinMipMap来快速找到和反射光相交的点。
SSR和光追思路是一样的,所以光追的很多效果,SSR可以直接得到。
Gamma校正
参考:
Gamma校正
Gamma校正: 美术创建贴图资源时,是基于显示器而创作的,但显示器的颜色亮度分布不是线性,光照计算时某些颜色亮度必须在线性空间中进行(如Diffuse贴图),所以读取贴图颜色后,需要先进行校正,再光照计算,最后再变回显示器的颜色分布。
校正步骤: 经过研究(可以看参考文章),采用pow(color, gamma)后,可以把颜色变到线性空间。这里的gamma值因显示器而异,大多数为2.2。所以在光照计算时,先对需要校正的颜色进行pow(color, gamma),然后进行光照计算,最后pow(color, 1.0f / gamma)再输出。
纹理
纹理采样
纹理主要是采样,采样方法很多,最简单的是点采样。
点采样:从顶点来对应纹理的对应坐标,再在光栅化时采用线性插值改变纹理中的坐标,坐标转换为定点数(所以会有小数部分舍入问题),最后绘制对应像素点。
还有更好的双线性插值,可以使图像变化更平缓(大概就是在纹理对应像素点附近的几个都给平均一下颜色)。
纹理也有透视修正的问题。(已解决)
未修正:
修正后:
纹理光照
纹理的光照处理可参考《3D游戏编程大师技巧》,在处理顶点时将所有顶点颜色置为RGB={1,1,1}(白色),然后和颜色着色一样计算光照,最后计算出的顶点对应的颜色值就是光照对纹理的影响,将这个影响加到纹理上即可。
Mipmap
参考:Why do images for textures on the iPhone need to have power-of-two dimensions?
纹理走样: 当纹理很大但在屏幕上对应于很小的一个区域,会导致纹理采样的坐标变化很快,采样结果将不正确,出现波纹或闪烁。根据傅里叶分析的结果,我们应该消除高频部分来解决此问题(纹理直接缩小时,其变化频率变高,即单位距离内纹素的变化加剧了)。
Mipmap: 多级渐远纹理。生成Mipmap一般需要纹理为正方形(也可以长宽不一致)。Mipmap是根据一个纹理生成多个比它更小的纹理,每次都以上一级的纹理为基础(初始级数为0),把长宽除以2,再对纹素进行相应变化,直到最后纹理大小为1×1。
储存上会多花费33%(大概1/3)的内存。
每次边长除以2: 对应的原理可以参考《3D游戏编程大师技巧》,从傅里叶分析可以得出,采样的频率严格大于样本原频率的2倍时才能还原出较准确的结果。这也是为什么Mipmap的生成是每次新边长为上一级的二分之一。
确定Mipmap级数: 最准确的方法是求出原始纹理面积与渲染区域面积的比值 t,再对比值求Log4t,若Log4t = 2.3,则可以采用第2级或第3级Mipmap。
因为每次求面积花销较大,还有一种近似方法是根据与视点的距离来确定级数,距离可以直接靠深度得出。
具体做法:规定深度大于一个值的统一采用最后一级,再将 [0,最深深度] 等分来对应不同级数。假设规定700之后统一采用7级Mipmap,那么在700前我们有7个Mipmap(一共7级,[0,7]有8个Mipmap,700后的占用最后一级,剩7个),[0,100)采用第0级,[100,200)采用第二级,以此类推。
优化
背面剔除
效果:
需要一个从平面指向观察点的向量,一个平面朝外的法向量,然后计算点积,如果结果小于等于0(一般要加等于,因为当夹角为90度时,这些多边形通常只有1个像素),就说明在背面,可以跳过不渲染。
透视修正
当图形输出到屏幕时,x值、y值、颜色值、纹理采样值等和坐标有关的值,原本的线性关系已经发生了改变,需要更正线性关系。
数学推导后可以发现它们和1/w(像素深度的倒数rhw)呈线性关系。
(参考:【3D游戏编程大师技巧】,第12章,12.5 )
解决:每个顶点在光栅化之前就将每个线性关系发生了变化的量与rhw相乘,光栅化时将rhw也进行插值计算,之后光栅化时之前该怎么插值就怎么插值,只是最后要得到相应的量时,要乘w(如纹理采样变为u*w,v*w)。
水平裁剪,垂直裁剪
考虑最终在屏幕坐标时,完全在屏幕外的三角形就直接不考虑了,但是有时可能一部分在屏幕上下侧/左右侧溢出,这时候用水平/垂直裁剪可以优化性能,避免不必要的光栅化。
当溢出在屏幕下/右侧时,比较简单,因为我的光栅化是从上至下,从左至右的,所以此时直接break出去即可。
当溢出在屏幕上侧时,计算y轴的溢出量dy=min_clip_y - y0(如果是整个窗口大小,min_clip_y就是0),再对其余需要改变的量增加相应的 di * dy ,最后改变y值起始值为min_clip_y即可。
注意变化过程中应保持浮点数,最后再向上取整变为整型,并进行相应修正。
当溢出在屏幕左侧时,同上,只不过是对x操作。
抗锯齿
抗锯齿也叫反走样(Anti-aliasing)。常见抗锯齿算法有:SSAA,MSAA,FXAA,TAA,DLSS。
-
SSAA(Super Sampling AA): 超采样抗锯齿,把画面整体放大一定倍数(4xSSAA就是放大4倍),进行上采样,再给下采样回原本的分辨率。显然很慢,效果很好。硬件支持,是光栅化时进行的。
以放大4倍为例,一个像素就有了4个子像素,对这4个子像素进行4次光照等计算。光照计算是很慢的,现在直接变成了4倍。 -
MSAA(Multi-Sampling AA): 多重采样抗锯齿,也是把画面放大,但是是计算子像素的被覆盖程度,最后算出中心点的颜色,最后只执行一次光照等计算,所以性能比SSAA高一些。
原理:对每个像素放置多个不同位置的采样点,光栅化时看三角形覆盖了几个采样点,再用覆盖的采样点和像素总的采样点作为依据来平均颜色。硬件支持,光栅化时进行。参考 -
FXAA(Fast approximate anti-aliasing): 快速近似抗锯齿,是一种后处理抗锯齿,就是在画面渲染完后,再通过像素颜色检测边缘(色彩差异太大时,不是边缘也被认为成边缘,精度有问题)。后处理技术没有倍数的概念,因为不存在放大。图形后处理,效率极高,效果一般。
-
TAA(Temporal Anti-Aliasing): 时域抗锯齿,Temporal AA尝试用在避免性能损失的情况近似Super Sampling AA的结果。它的做法一句话总结就是,把样本分布到过去的N帧中去,然后每一帧从过去的N帧中取得样本信息然后Filter,达到N倍Super Sampling的效果。参考
-
DLSS(Deep Learning Super Sampling): 深度学习超级采样,英伟达的新抗锯齿技术。
双线性滤波 / 三线性滤波 / 各种滤波
主要是对纹理采样的反走样。
先详细介绍双线性滤波。
普通的纹理采样是获取到纹素坐标后,直接截取为整形,然后采样,这叫点采样。显然这样直接截取丢失了部分信息。
双线性滤波
设纹素浮点坐标为(u,v),我们可以从周围的4个采样点获取信息,再根据某些权值(一般是面积占比)来平均。
先考虑横向,假设采样坐标为(7.4,1),那么左边u_0为(7,1),右边u_1为(8,1),对左右进行采样后,左边的采样值*=(8-7.4=0.6)(可能会奇怪为什么不是7.4-7,可以用右边的值 - 总变化值*当前点到右边距离=当前点值 来推导),右边的采样值*=(7.4-7)。
然后同时考虑横向纵向,若采样坐标为(7.4,1.2),则周围4个采样点为(7,1),(7,2),(8,1),(8,2)。我们求得上下两边对横向的线性插值后,可以算出点(7,1.2),(8,1.2),然后再考虑纵向的插值(所以一共进行3次插值),即可求出当前采样点的双线性滤波。
三线性滤波
三线性滤波有几种,一种是考虑3维空间立方体的8个子立方体来线性插值,这里不讨论这个。还有一种是综合Mip-mapping和双线性插值。
假设算出该去第4.2个Mip-mapping采样,那么就不是简单截取直接去4或者5个Mip-mapping采样,而是去第4和第5个Mip-mapping去采样,在这个采样中进行双线性滤波得到P4(第4个的),P5(第5个),再得到最终P=(1-0.2)*P4+0.2*P5。
参考1(这个的双线性插值计算推导有的问题,但是扩展得比较多,也讲了三线性滤波)
参考2(双线性滤波和插值推导)
各向异性过滤
参考:GAMES101 , 时间点1:02
MipMap总是宽高同时除以2,这样有时得到的结果是不太正确的(比如:1.像素转换后有时对应一个长方形的纹理区域,此时用MipMap的正方形就会不够精确。2.远处的像素对应的MipMap级别可能很大,导致完全糊掉,丢失细节。此时若只缩小纹理的长或宽,而不是同时缩小,就可以保留细节)。
把生成MipMap时,不同时缩小宽高,而是分别缩小,得到一系列子纹理,再去这些纹理采样,就叫各向异性过滤(Anisotropic Filtering )。
储存上会多花费3倍的内存(比MipMap多很多)。

延迟着色(Deferred Shading)
参考:
【《Real-Time Rendering 3rd》 提炼总结】(七) 第七章续 · 延迟渲染(Deferred Rendering)的前生今世
延迟渲染与MSAA的那些事
正向渲染:
简要概括:先进行着色,再进行深度测试。
传统的渲染方法就叫正向渲染。对所有的物体执行完整光栅化,这时有部分物体的像素会被遮盖住而浪费了绘制花费,特别是光源等做了无端的计算。
仅考虑光照,此时 总计算量 = 总物体片元数 × 总光源数 总计算量 = 总物体片元数 \times 总光源数 总计算量=总物体片元数×总光源数。
当然这里很容易想到渲染两次场景,第一次只记录深度,第二次渲染时直接深度剔除,也算避免了浪费计算。但是这个还是有一些问题,后面再详细说明。
延迟渲染:
简要概括:先深度测试,再进行着色,将本来在物空间(三维空间)进行光照计算放到了像空间(二维空间)进行处理。
为了避免光照等效果的浪费计算,那么可以在计算之前记录下需要用到的值(像素的世界坐标位置、法线、反射等),因为多个物体堆叠到最后,只会渲染最前面的部分,所以只需要记录最终所用的就行了。把这个值放入叫做G-buffer(Geometry buffer)的纹理中,然后再对根据这个纹理的信息执行光照等计算。
此时 总计算量 = 屏幕片元数 × 总光源数 总计算量 = 屏幕片元数 \times 总光源数 总计算量=屏幕片元数×总光源数。显然屏幕片元数多数时候小于总物体片元数。
延迟渲染 vs 正向渲染+提前深度测试:
参考:Early Depth Test + Forward 和 Deferred Rendering 比较?
Deferred render vs forward render + early-z
注意这里的深度测试对应的是depth prepass (early depth pass),而不是硬件支持的那个early-z。
先来看看两种做法的大致流程:
- 延迟渲染:1.执行场景渲染,但渲染到G-buffer上。2.把G-buffer作为纹理,渲染一个占据屏幕的简单四边形(或一个大三角形,其实更推荐大三角形)。
- 正向渲染+提前深度测试:1.渲染一遍场景,但不进行片元着色,仅记录深度值。2.再渲染一次场景,此时丢弃深度测试不通过的。
延迟渲染看着像是渲染了两次,但是第二次只渲染一个2维图形,顶点处理可以忽略不记了,总的来说可以算作延迟渲染只渲染了一次场景。
正向渲染+提前深度测试虽然第一次没用片元着色,但两次都要处理顶点,这个开销其实是比较大的。所以速度上还是比延迟渲染慢一些。
空间划分算法
参考:GAMES101_Lecture_14 --P16
用于快速剔除物体、碰撞检测等。
有四叉树(八叉树)、KD树、BSP树、BVH(层次包围盒)等算法。目前用得较多的是BVH算法。
四叉树: 每次均分4个子树出来。
KD树: 每次只划分两个子树,划分按照维度轮流来(三维就是先x轴划分,再y轴划分,再z轴划分)。
BVH: 每次构建几个包围盒各自包住一部分物体,子树个数就是包围盒的个数。
Z-test,Early-z和Pre-z
参考
Z-test: 执行完PS的着色计算后,根据深度缓存的值,判断是否丢弃该像素。
Early-z: 光栅化之后,PS之前,硬件自动只判断深度,决定是否继续执行后面的PS。(比如先写了一个深度为1的像素,现在碰到一个深度为2的像素,发现被遮挡了,跳过PS)。有时会自动关闭Early-z(比如开启Alpha测试、PS更改深度、UAV)。
Pre-z: 如果开启了Alpha测试,需要判断完全透明的部分,来绘制其后方不透明像素,此时Early-z自动关闭,但所有像素均进行PS,开销较大。可以在Base Pass前加一个Pre-Z Pass,该Pass开启Alpha测试,且只写入深度,得到一张深度图。
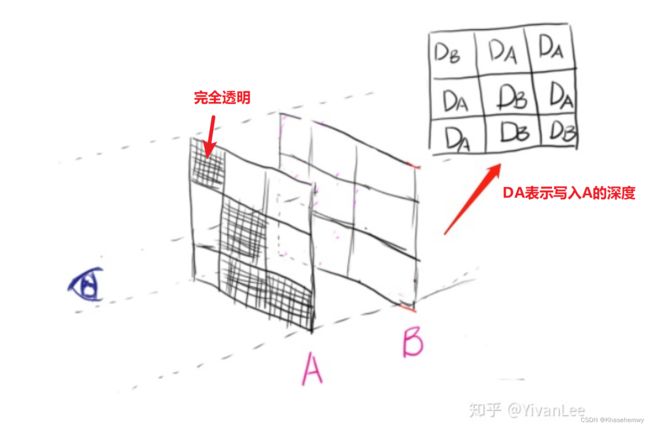
然后Base Pass关闭Alpha测试,将深度测试设为Equal,根据深度图来决定是否绘制。此时会Early-z跳过被遮盖的像素和完全透明的像素(因为和深度图测试Equal,不通过)。
当然,Pre-z也可以解决先绘制后方,再绘制前方导致Early-z无效的问题,不过得多一个Pass的开销。
反向z(reserved-z)
反向z投影矩阵推导
Reversed-Z
reserved-z: 用于减少远处z-fighting现象。
传统管线中,透视投影后,在NDC坐标时,z范围为[0,1],且非线性变化,在近平面附近变化剧烈。因为float也在0附近精度高,近平面z值变化剧烈 + float在0值附近精度高,两者叠加,就导致了远处很容易出现z-fighting问题。
透视投影后,z值在近平面变化剧烈,这一点是难以更改的。那么可以想到,将z值与float的对应关系进行更改,近平面对应float的1,远平面对应float的0,从而两者互补,以使z值在float范围上均匀分布。
透视投影矩阵推导:
我们知道,将 [近平面,远平面] 映射至 [0,1] 的矩阵推导如下:
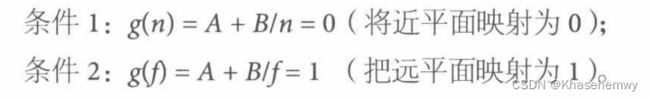
其中A、B表示矩阵中的两个值。(根据行、列向量的使用,对应位置可能不同)
那么很容易得出,将 [近平面,远平面] 映射至 [1,0] 的推导为:
z v i e w = = n e a r z_{view} == near zview==near 时, z n d c = A + B / n = 1 {z_{ndc} = A + B/n = 1} zndc=A+B/n=1
z v i e w = = f a r z_{view} == far zview==far 时, z n d c = A + B / f = 0 {z_{ndc} = A + B/f = 0} zndc=A+B/f=0
最后算出(对于列向量的投影矩阵):

欧拉角、四元数
欧拉角万向节死锁: 仅在使用物体坐标轴(动态欧拉角)时,会出现死锁问题。死锁意义为,在一次旋转中,某一轴可被其他轴所取代(丢失轴),进而导致无法正确插值。
四元数: xyz表示某一轴,w表示绕该轴旋转的弧度。使用四元数进行球面线性插值,可以得到正确插值结果。
外部模型导入
效果:
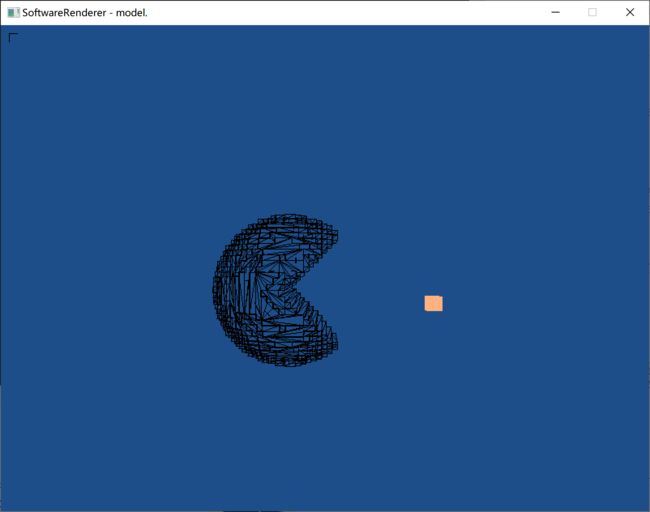
借助了assimp库,搞渲染不会还去写个模型读取的东西吧,所以直接用库了,也仅仅是导入模型而已,对渲染的理解没有影响。
引用库说难也不难,就是用个工具而已;说简单也不简单,要去看具体使用方法,步骤比较繁琐。
目前只把3D模型的顶点数据获取了,然后可以画线框图。纹理这块还没处理好。