算法笔记-第九章-二叉查找树
算法笔记-第九章-二叉查找树
- 什么是二叉查找树
-
- 大佬讲解一
- 大佬讲解二
- 二叉查找树的建立
- 二叉查找树的判定
- 还原二叉查找树
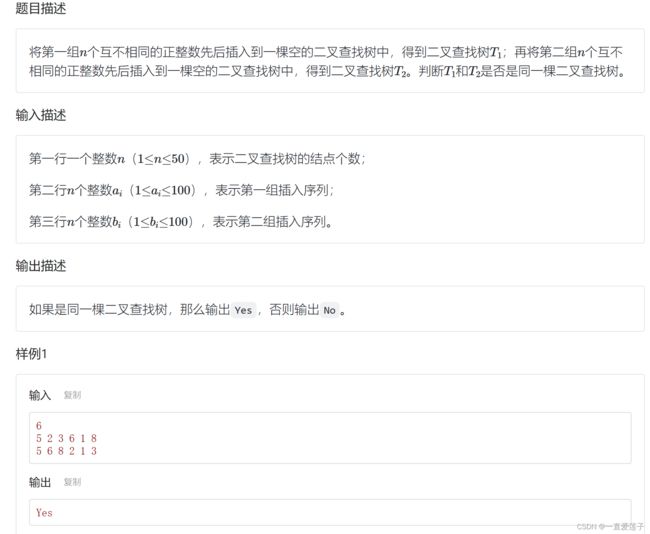
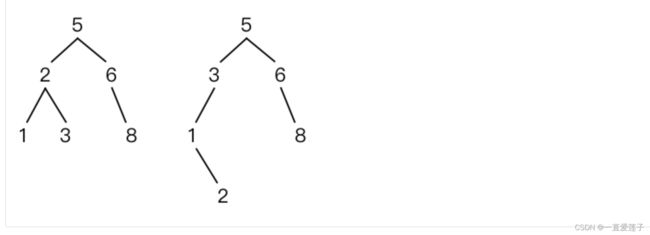
- 相同的二叉查找树
- 填充二叉查找树
什么是二叉查找树
若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。
若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。
它的左、右树又分为⼆叉排序树
显然,二叉排序树与二叉树一样,也是通过递归的形式定义的。因此,它的操作也都是基于递归的方式。
大佬讲解一
大佬讲解二
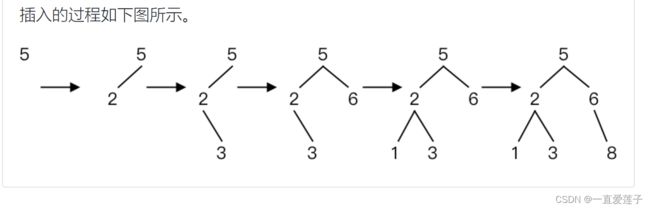
二叉查找树的建立
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 50;
struct Node {
int data;
int l, r;
} nodes[MAXN];
int nodeCount = 0;
int newNode(int data) {
nodes[nodeCount].data = data;
nodes[nodeCount].l = nodes[nodeCount].r = -1;
return nodeCount++;
}
int insert(int root, int data) {
if (root == -1) {
return newNode(data);
}
if (data < nodes[root].data) {
nodes[root].l = insert(nodes[root].l, data);
}
else {
nodes[root].r = insert(nodes[root].r, data);
}
return root;
}
vector<int> pre;
void preOrder(int root) {
if (root == -1) {
return;
}
pre.push_back(nodes[root].data);
preOrder(nodes[root].l);
preOrder(nodes[root].r);
}
int main() {
int n, data, root = -1;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &data);
root = insert(root, data);
}
preOrder(root);
for (int i = 0; i < (int)pre.size(); i++) {
printf("%d", pre[i]);
if (i < (int)pre.size() - 1) {
printf(" ");
}
}
return 0;
}
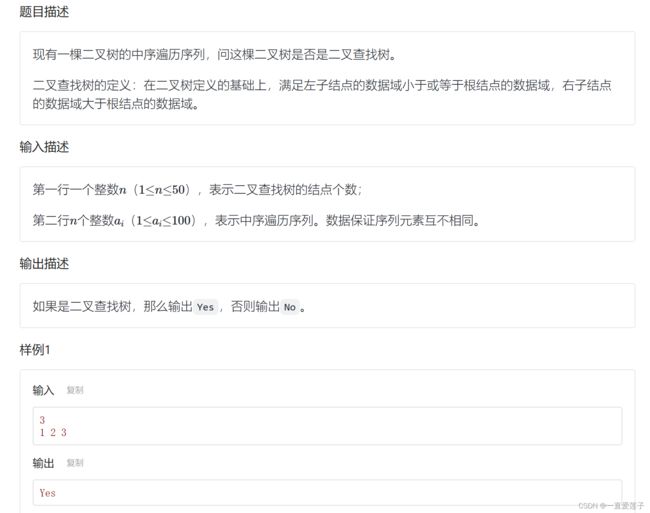
二叉查找树的判定
#include <cstdio>
#include <vector>
using namespace std;
vector<int> in;
bool isBST() {
for (int i = 1; i < in.size(); i++) {
if (in[i] <= in[i - 1]) {
return false;
}
}
return true;
}
int main() {
int n, x;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &x);
in.push_back(x);
}
printf(isBST() ? "Yes" : "No");
return 0;
}
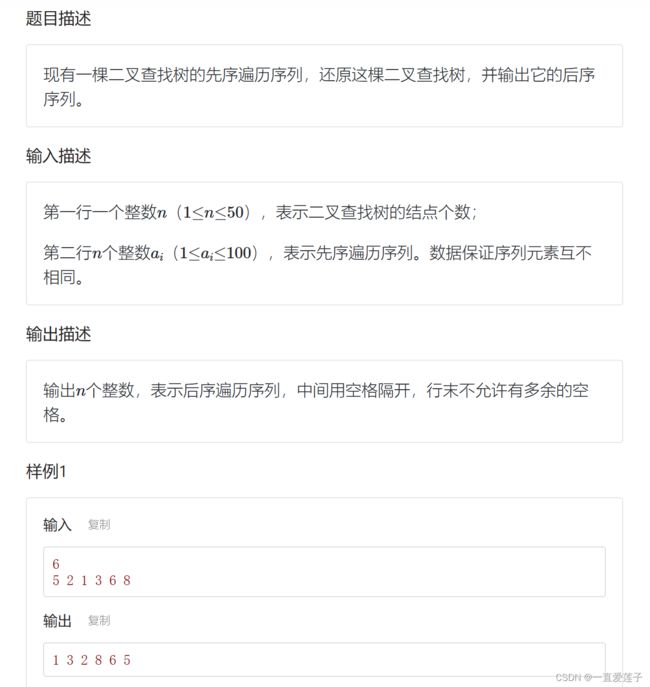
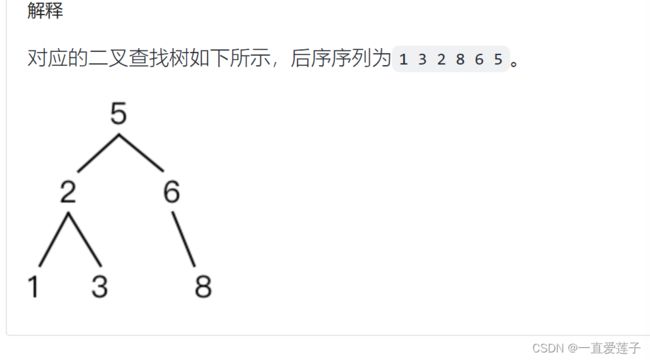
还原二叉查找树
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 50;
struct Node {
int data;
int l, r;
} nodes[MAXN];
int nodeCount = 0;
int newNode(int data) {
nodes[nodeCount].data = data;
nodes[nodeCount].l = nodes[nodeCount].r = -1;
return nodeCount++;
}
vector<int> pre, in, post;
int buildTree(int preL, int preR, int inL, int inR) {
if (preL > preR) {
return -1;
}
int root = newNode(pre[preL]);
int inIndexOfRoot;
for (int i = inL; i <= inR; i++) {
if (in[i] == nodes[root].data) {
inIndexOfRoot = i;
break;
}
}
int leftCount = inIndexOfRoot - inL;
nodes[root].l = buildTree(preL + 1, preL + leftCount, inL, inIndexOfRoot - 1);
nodes[root].r = buildTree(preL + leftCount + 1, preR, inIndexOfRoot + 1, inR);
return root;
}
void postOrder(int root) {
if (root == -1) {
return;
}
postOrder(nodes[root].l);
postOrder(nodes[root].r);
post.push_back(nodes[root].data);
}
int main() {
int n, x;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &x);
pre.push_back(x);
}
in = pre;
sort(in.begin(), in.end());
int root = buildTree(0, n - 1, 0, n - 1);
postOrder(root);
for (int i = 0; i < (int)post.size(); i++) {
printf("%d", post[i]);
if (i < (int)post.size() - 1) {
printf(" ");
}
}
return 0;
}
相同的二叉查找树
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 50 * 2;
struct Node {
int data;
int l, r;
} nodes[MAXN];
int nodeCount = 0;
int newNode(int data) {
nodes[nodeCount].data = data;
nodes[nodeCount].l = nodes[nodeCount].r = -1;
return nodeCount++;
}
int insert(int root, int data) {
if (root == -1) {
return newNode(data);
}
if (data < nodes[root].data) {
nodes[root].l = insert(nodes[root].l, data);
} else {
nodes[root].r = insert(nodes[root].r, data);
}
return root;
}
void preOrder(int root, vector<int>& pre) {
if (root == -1) {
return;
}
pre.push_back(nodes[root].data);
preOrder(nodes[root].l, pre);
preOrder(nodes[root].r, pre);
}
int main() {
int n, data;
scanf("%d", &n);
int root1 = -1, root2 = -1;
for (int i = 0; i < n; i++) {
scanf("%d", &data);
root1 = insert(root1, data);
}
for (int i = 0; i < n; i++) {
scanf("%d", &data);
root2 = insert(root2, data);
}
vector<int> pre1, pre2;
preOrder(root1, pre1);
preOrder(root2, pre2);
printf(pre1 == pre2 ? "Yes" : "No");
return 0;
}
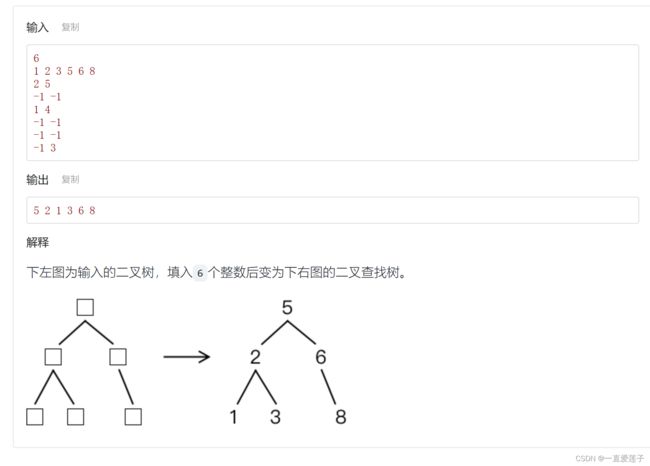
填充二叉查找树
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 50;
struct Node {
int data;
int l, r;
} nodes[MAXN];
vector<int> pre, in;
int inIdx = 0;
void inOrder(int root) {
if (root == -1) {
return;
}
inOrder(nodes[root].l);
nodes[root].data = in[inIdx++];
inOrder(nodes[root].r);
}
void preOrder(int root) {
if (root == -1) {
return;
}
pre.push_back(nodes[root].data);
preOrder(nodes[root].l);
preOrder(nodes[root].r);
}
int main() {
int n, x;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &x);
in.push_back(x);
}
for (int i = 0; i < n; i++) {
scanf("%d%d", &nodes[i].l, &nodes[i].r);
}
sort(in.begin(), in.end());
inOrder(0);
preOrder(0);
for (int i = 0; i < (int)pre.size(); i++) {
printf("%d", pre[i]);
if (i < (int)pre.size() - 1) {
printf(" ");
}
}
return 0;
}