剑指offer—位运算专题

前言

本篇文章记录剑指offer（第二版）位运算专题的全部题目，并配合详细的讲解

---

题目列表

JZ65 不用加减乘除做加法
JZ15 二进制中1的个数
JZ16 数值的整数次方
JZ56 数组中只出现一次的两个数字
JZ64 求1+2+3+…+n

1.JZ65 不用加减乘除做加法

描述

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

数据范围：两个数都满足 0≤n≤1000
进阶：空间复杂度 O(1)，时间复杂度 O(1)

思路

首先看十进制是如何做的： 5+7=12，三步走
第一步：相加各位的值，不算进位，得到2。
第二步：计算进位值，得到10. 如果这一步的进位值为0，那么第一步得到的值就是最终结果。

第三步：重复上述两步，只是相加的值变成上述两步的得到的结果2和10，得到12。

同样我们可以用三步走的方式计算二进制值相加： 101，111
第一步：相加各位的值，不算进位，得到010，二进制每位相加就相当于各位做异或操作，101^111。

第二步：计算进位值，得到1010，相当于各位做与操作得到101，再向左移一位得到1010，(101&111)<<1。

第三步重复上述两步， 各位相加 010^1010=1000，进位值为100=(010&1010)<<1。
继续重复上述两步：1000^100 = 1100，进位值为0，跳出循环，1100为最终结果。

解答

class Solution:
    def Add(self, num1, num2):
        x = 0xffffffff
        num1,num2 = num1&x,num2&x # 若有负数，以补码形式展现
        while num2:
            num1,num2 = (num1 ^ num2),((num1&num2)<<1) & x
        return num1 if num1 < 0x7ffffff else ~(num1^x)

注释

Python，Java 等语言中的数字都是以补码形式存储的。但 Python 没有 int , long 等不同长度变量，即在编程时无变量位数的概念。
获取负数的补码： 需要将数字与十六进制数 0xffffffff 相与。可理解为舍去此数字 32 位以上的数字（将 32 位以上都变为 00 ），从无限长度变为一个 32 位整数。
返回前数字还原： 若补码 a 为负数（ 0x7fffffff 是最大的正数的补码 ），需执行 ~(a ^ x) 操作，将补码还原至 Python 的存储格式。 a ^ x 运算将 1 至 32 位按位取反； ~ 运算是将整个数字取反；因此， ~(a ^ x) 是将 32 位以上的位取反，1 至 32 位不变。

print(hex(1)) # = 0x1 补码
print(hex(-1)) # = -0x1 负号 + 原码 （ Python 特色，Java 会直接输出补码）

print(hex(1 & 0xffffffff)) # = 0x1 正数补码
print(hex(-1 & 0xffffffff)) # = 0xffffffff 负数补码

print(-1 & 0xffffffff) # = 4294967295 （ Python 将其认为正数）

参考：
https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof/solution/mian-shi-ti-65-bu-yong-jia-jian-cheng-chu-zuo-ji-7/

2.JZ15 二进制中1的个数

描述

输入一个整数 n ，输出该数32位二进制表示中1的个数。其中负数用补码表示。

数据范围：- 2³¹ <=n<=2³¹ -1
即范围为：−2147483648<=n<=2147483647

思路

1）首先由于负数需要用补码表示，在Python中由上一题可知，可以通过将整数n与0xffffffff相与得到补码。
2）题目要求统计二进制中1的个数，由于位运算操作n&(n-1) 可以将n的二进制表示的最后一个1去掉，因此循环遍历即可。

解答

class Solution:
    def NumberOf1(self, n):
        x = 0xffffffff
        n = n&x
        count = 0
        while n:
            n = n&(n-1)
            count += 1
        return count

3.JZ16 数值的整数次方

描述

实现函数 double Power(double base, int exponent)，求base的exponent次方。

注意：
1.保证base和exponent不同时为0。
2.不得使用库函数，同时不需要考虑大数问题
3.有特殊判题，不用考虑小数点后面0的位数。

进阶：空间复杂度O(1) ，时间复杂度O(N)

思路

1)针对指数为负数进行处理：指数设为正数，底数设为1/底数
2）假设求x⁶,则6 = 1100，可以看成是0 *2⁰+ 0 * 2¹+1 *2²+1 *2³,所以x⁶可以写成如下所示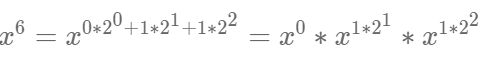
因此我们只需要将其看成3部分，分别算出，在连乘即可

解答

class Solution:
    def Power(self , base, exponent):
        # 解决指数为负数问题
        if exponent<0:
            exponent = -exponent
            base = 1/base
        ret = 1.0
        x = base
        while exponent:
        # 对于二进制数，遇到位数是1的就乘到答案中。
            if exponent&1:
                ret *=x
            x *= x
            exponent = exponent>>1
        return ret

4.JZ56 数组中只出现一次的两个数字

描述

一个整型数组里除了两个数字只出现一次，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。

数据范围：数组长度 2≤n≤1000，数组中每个数的大小 0 要求：空间复杂度 O(1)，时间复杂度 O(n)

提示：输出时按非降序排列。

思路

1）若题目改为 一个整型数组里除了两个数字只出现一次，其他的数字都出现了两次 可以很方便解答，只需要利用异或操作的特点：A⊕A = 0，即对自身异或为0，可以将数组元素异或遍历，最后的结果就是所需的答案。

def singleNumber(self, nums: List[int]) -> List[int]:
    x = 0
    for num in nums:  # 1. 遍历 nums 执行异或运算
        x ^= num      
    return x;         # 2. 返回出现一次的数字 x

2）但该题目改为数组中只出现一次的两个数字，就需要考虑分组操作，即将这两个数字分别放在不同的组里，然后分别对不同组进行遍历异或，就可以得到最后的答案，那么现在的问题就是如何分组？
3）仿照区分奇偶的方法，将不同的数 & 0001就可以区分奇偶，所以我们也可以将这两个数和一个数相与进行区分，问题便转换为哪个数可以用来做区分？此处可以利用异或⊕的性质，不同的数异或为1 例如 1⊕0 = 1,1⊕1=0，0⊕0 = 0,0⊕1=0，因此我们前面通过遍历异或得到了这两个数的异或结果n，此处只需找到n二进制表示末尾为1的位置即可，如下所示

  x,y,n,m = 0,0,0,1
  for i in array:
      n ^= i       # 遍历异或
  while m&n==0:
      m <<= 1       # 找出可以区分x,y的值

关于为什么不用n直接进行区分的问题：n的二进制表示中有许多位都有1，比如 n = 1100⊕0110 = 1010，如果我们用n分别和这两个数进行相与，得到了1000和0010，根本没有办法进行区分，而如果只取n的末尾1元素，m = 0010，就可以将两个区分为0000和0010，通过结果是否为0进行区分。

整体步骤如图所示：

参考：
https://leetcode-cn.com/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/solution/jian-zhi-offer-56-i-shu-zu-zhong-shu-zi-tykom/

解答

class Solution:
    def FindNumsAppearOnce(self , array):
        x,y,n,m = 0,0,0,1
        for i in array:
            n ^= i       # 遍历异或
        while m&n==0:
            m <<= 1       # 找出可以区分x,y的值
        for i in array:   # 分别对每组进行异或
            if i&m !=0:
                x ^= i
            else:
                y ^=i
                
        return [x,y] if x<y else [y,x]

5.JZ64 求1+2+3+…+n

描述

求1+2+3+…+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

数据范围：0 进阶： 空间复杂度 O(1) ，时间复杂度 O(n)

思路

参考：
https://leetcode-cn.com/problems/qiu-12n-lcof/solution/mian-shi-ti-64-qiu-1-2-nluo-ji-fu-duan-lu-qing-xi-/

解答

class Solution:
    def __init__(self):
        self.res = 0
    def Sum_Solution(self , n):
        n > 1 and self.Sum_Solution(n-1);
        self.res += n
        return self.res;