【代码随想录刷题】Day11 栈与队列

【20】有效的括号
【1047】 删除字符串中的所有相邻重复项
【150】逆波兰表达式求值

1.【20】有效的括号

【20】有效的括号

1.1题目描述

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 每个右括号都有一个对应的相同类型的左括号。

示例 1：
输入：s = “()”
输出：true

示例 2：
输入：s = “()[]{}”
输出：true

示例 3：
输入：s = “(]”
输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 ‘()[]{}’ 组成

1.2 解题思路

括号匹配是使用栈解决的经典问题

前言

• 题意其实就像我们在写代码的过程中，要求括号的顺序是一样的，有左括号，相应的位置必须要有右括号。

• 如果还记得编译原理的话，编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑，也是使用了栈这种数据结构。

• 再举个例子，linux系统中，cd这个进入目录的命令我们应该再熟悉不过了。

cd a/b/c../../

这个命令最后进入a目录，系统是如何知道进入了a目录呢 ，这就是栈的应用（其实可以出一道相应的面试题了）

所以栈在计算机领域中应用是非常广泛的。

进入正题

由于栈结构的特殊性，非常适合做对称匹配类的题目。

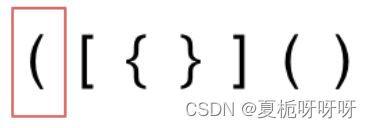
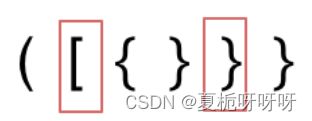
首先要清楚字符串里的括号不匹配有几种情况，这里有三种：

• 1.第一种情况，字符串里左方向的括号多余了 ，所以不匹配。
  

• 2.第二种情况，括号没有多余，但是 括号的类型没有匹配上。
  

• 3.第三种情况，字符串里右方向的括号多余了，所以不匹配。
  

• 最后，那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。

匹配过程示意图：

从图中可以看出，栈中剩下“)”，也就是栈不为空，最后返回false。

1.3 java代码实现

时间复杂度: O(n)
空间复杂度: O(n)

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack=new Stack<>();
        char ch;
        for (int i=0;i<s.length();i++){
            ch=s.charAt(i);
            //遇到左括号，就把右括号入栈
            if (ch=='('){
                stack.push(')');
            }else if (ch=='{'){
                stack.push('}');
            }else if (ch=='['){
                stack.push(']');
            }else if (stack.isEmpty() || stack.peek() !=ch){
                return false;
            }else {
                //如果是右括号  判断是否和栈顶元素匹配
                stack.pop();
            }

        }
        //最后判断栈中元素是否匹配
        return stack.isEmpty();

    }
}

2.【1047】 删除字符串中的所有相邻重复项

【1047】 删除字符串中的所有相邻重复项

2.1题目描述

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：
输入：“abbaca”
输出：“ca”

解释：
例如，在 “abbaca” 中，我们可以删除 “bb” 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”，其中又只有 “aa” 可以执行重复项删除操作，所以最后的字符串为 “ca”。

提示：

• 1 <= S.length <= 20000
• S 仅由小写英文字母组成。

2.2 解题思路

本题中要删除相邻相同元素，相对于【20】有效的括号来说其实也是匹配问题，【20】有效的括号 是匹配左右括号，本题是匹配相邻元素，最后都是做消除的操作。

本题也是用栈来解决的经典题目。

那么栈里应该放的是什么元素呢？

• 我们在删除相邻重复项的时候，其实就是要知道当前遍历的这个元素，我们在前一位是不是遍历过一样数值的元素，那么如何记录前面遍历过的元素呢？

• 所以就是用栈来存放，那么栈的目的，就是存放遍历过的元素，当遍历当前的这个元素的时候，去栈里看一下我们是不是遍历过相同数值的相邻元素。

• 然后再去做对应的消除操作，最后从栈中弹出剩余元素。

• 因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。

2.3 java代码实现

方式一：使用Deque作为堆栈
时间复杂度: O(n)
空间复杂度: O(n)

class Solution {
    public String removeDuplicates(String s) {
        /**
         * 使用Deque作为堆栈
         */
        //ArrayDeque会比LinkedList在除了删除元素这一点外会快一点
        ArrayDeque<Character> deque=new ArrayDeque<>();
        char ch;
        for (int i=0;i<s.length();i++){
            ch=s.charAt(i);
            if (deque.isEmpty() || deque.peek() !=ch){
                deque.push(ch);
            }else {
                deque.pop();
            }
        }
        String str="";
        //剩下的元素就是不重复的
        while (!deque.isEmpty()){
            str=deque.pop()+str;
        }
        return str;
    }
}

方式二：拿字符串直接作为栈，这样省去了还要转为字符串的操作
时间复杂度: O(n)
空间复杂度: O(1)

class Solution {
    public String removeDuplicates(String s) {
        /**
         * 拿字符串直接作为栈，这样省去了还要转为字符串的操作
         */
        //使用res作为栈
        StringBuffer res=new StringBuffer();
        //top是res的长度
        int top=-1;
        for (int i=0;i<s.length();i++){
            char ch=s.charAt(i);

            //当top>0时，说明栈中有元素，
            // 此时如果当前字符和栈中字符相等，弹出栈顶字符，同时top--
            if (top>=0 && res.charAt(top)==ch){
                res.deleteCharAt(top);
                top--;
            }else {//否则，将该字符入栈，同时top++
                res.append(ch);
                top++;
            }
        }
        return res.toString();


    }
}

3.【150】逆波兰表达式求值

【150】逆波兰表达式求值

3.1题目描述

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：
输入：tokens = [“2”,“1”,“+”,“3”,“*”]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：
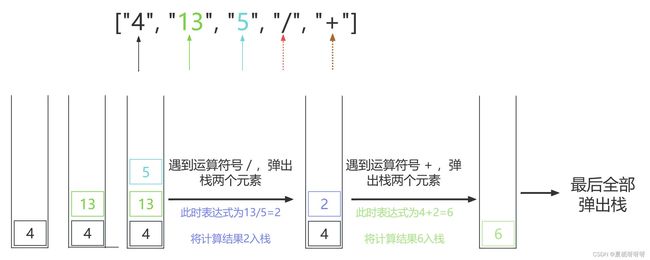
输入：tokens = [“4”,“13”,“5”,“/”,“+”]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：
输入：tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

• 1 <= tokens.length <= 104
• tokens[i] 是一个算符（“+”、“-”、“*” 或 “/”），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

3.2 解题思路

• 逆波兰表达式相当于是二叉树中的后序遍历。 我们可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。

• 本题中的每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这就是一个相邻字符串消除的过程，和【1047】 删除字符串中的所有相邻重复项中的消消乐游戏就非常像了。

如果想详细了解前缀和后缀表达式，可以看这篇文章：
前缀和后缀表达式

3.3 java代码实现

时间复杂度: O(n)
空间复杂度: O(n)

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack=new LinkedList<>();
        for (String s : tokens) {
            if ("+".equals(s)){
                stack.push(stack.pop()+stack.pop());
            }else if ("-".equals(s)){
                stack.push(-stack.pop()+stack.pop());//注意-和/
            }else if ("*".equals(s)){
                stack.push(stack.pop()*stack.pop());
            }else if ("/".equals(s)){
                int temp1=stack.pop();
                int temp2=stack.pop();

                stack.push(temp2 / temp1);//注意'/'
            }else {
                stack.push(Integer.valueOf(s));
            }
        }
        return stack.pop();

    }
}