算法思想-回溯

回溯(Back-Tracing)

回溯法值得就是一种搜索，或是一种组织得井井有条的，避免不必要步骤的搜索法。
回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。
回溯法指导思想——从一个点开始，按照规则顺序往前走，走的通则继续走；走不通，就掉头，掉头还是不通，就再掉头。因此也是多使用递归法实现回溯。

四皇后问题

四皇后问题类似于迷宫探索，其规则为

八皇后问题是一个古老而著名的问题，是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出：在8X8格的国际象棋上摆放八个皇后（棋子），使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上

假如从第一行开始，将一个皇后棋子放在第一行第二列，那么下图中，只有对勾位置可以放置第二颗皇后棋。按照这个规则，若采用穷举，则需要进行444*4= 256次。

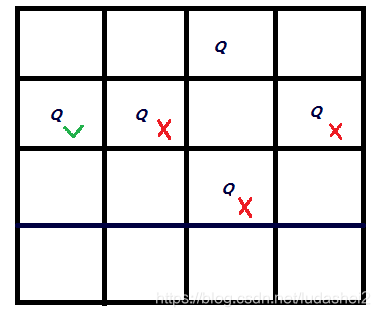
如果利用回溯，在选定一个起始点后，按照行列作为步长，依次尝试所有坐标位置，其中深度优先遍历会选择在某一行找到合适坐标后，优先选择向下一行探索，这样可快速找到一套正确的布局方式。如果依次选取第一行的每一列作为起始点，便可找到所有正确的布局方式，4皇后问题找到所有遍历布局方式的循环次数也只有62次，远低于穷举法的256次。

计算过程

回溯法的思路很简单，基本上就是有规则的遍历尝试，现在以四皇后的求解过程简单分析一下回溯思想

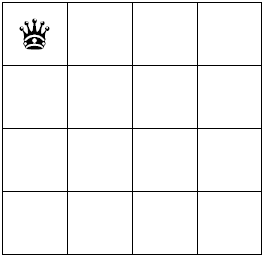
1. 第一行开始

首先在第1行的第1列放置一枚皇后棋子；判断是否安全，判断放下该棋子后他的正副对角线、同行、同列是否有皇后棋子，有的话就是不安全，
那么要尝试第1行第2列，但实际肯定是安全的（目前只放了一个棋子）因此这样行的其它列不用去尝试了。

2. 向下到第二行继续
继续在第2行的第1列放置一枚皇后棋子，判断是否安全，判断放下该棋子后他的正副对角线、同行、同列
是否有皇后棋子，很不幸，他的同列有皇后棋子，不安全。继续尝试下一列，直到第3列时才安全，停止尝试，转到下一行。

3. 向下到第三行继续
继续在第3行的第1列放置一枚皇后棋子，判断是否安全，判断放下该棋子后他的正副对角线、同行、同列是否有皇后棋子，更加不幸，他的同列有皇后棋子，不安全。继续尝试下一列，直到第最后列时都不安全。此时只能跳到上一行。

4. 返回到第二行继续
返回在第2行放置一枚皇后棋子，前面已经确定第二列不安全、第三列对于下一行来说也不安全，那就只能继续放到地4列判断是否安全，即判断放下该棋子后他的正副对角线、同行、同列
是否有皇后棋子，还好是安全的，可以转到下一行。

5. 向下到第三行继续
再次来到第3行，不同于上一步“ 返回到第二行”，由于第二行的放置位置已经改变，因此第3行必须从头重试，因此从第3行第1列开始判断是否安全，很幸运，在第3行
第2列时已安全，继续到下一行。

6. 向下到第四行继续
来到第4行，遍历四列后发现，都不安全，此时要向上一行返回，但是第3行除了第2列以外，都不安全，怎么办？继续返回到第2行。但是第二行四列都是过啦，无论怎么放，往下走都是死路，怎么办？乖乖回到第1行。

---

经过以上6步，又回到了原点，一个棋子也没有放好，但是，我们已经确认一个事实：第1行第1列不能放。怎么办？继续尝试第1行第2列！尝试过程如下：

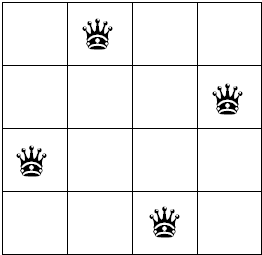
与穷举的比较

回溯法看似与穷举法相同，但是重复步骤是少很多的。例如在以第1行第1列开始的尝试，如果是穷举，需要尝试 144*4= 64次，但是回溯只进行了14次就将第1行第1列排除。而整个棋盘遍历所需要的尝试次数实际为62次，也是远低于穷举的256次。原因就在于回溯法，在发现尝试失败回退时，是记住上一步的执行状态的，不需要从新执行上一步的全部过程，而是从跳到这一步的”端点“处继续执行，即回溯是记忆的。

代码实现

回溯可使用遍历与递归实现，若使用递归，可以将每一行的的各列遍历作为一次递归。在某一行的某一列找到合适位置，就继续递归到下一行继续遍历下一行的各列；找不到合适位置则该次递归结束，返回到上一行；当然每一次递归都需要记录合适的列位置，当位置数量与所需放置的棋子数量一致时，可选择打印记录的列（一个解）结束遍历与递归，也可选择继续找到所有解。

#include
#include
#include 
#define M 4
int queue[M] = { -1 };//用来保存4个皇后的列数
int count = 0;//方法总数
int loopcnt =0;
char map[4][4] = {"0000","0000","0000","0000"};
void printmap(char map[4][4])
{

        for (int i = 0; i < M; i++)
        {
                for (int j = 0; j < M; j++)
                {
                        printf("%c", map[i][j]);
                }

                printf("\n");
        }
        printf("-------------------------------------------\n");
}
int issafe(int row, int column)//用于判断该位置是否安全
{
        for (int i = 0; i<row; i++)//遍历前面放置了皇后的行
        {
                if (queue[i] == column) return 0;//同一列不安全
                if ((row - i) == (column - queue[i])) return 0;//同一主对角线，行之差和列之差相等
                if ((row - i) + (column - queue[i])==0) return 0;//副对角线，行之差列之差的和为0
        }
        return 1;
}

void pickqueue(int num) //num既是已摆放的皇后棋子数目，也是行号，因为每一行必定会放置一个皇后棋子
{
        for (int i = 0; i<M; i++)//遍历所有列数，找出能放的列
        {
                loopcnt++;
                if (issafe(num, i))//判断当前皇后放在哪列式安全的
                {
                        queue[num] = i;//保存当前列数
                        if (num == 3)//满4个皇后
                        {
                                count++;
                                for (int j = 0; j < M; j++)
                                {
                                        map[j][queue[j]] = '1';
                                }
                                printmap(map);
                                memset(map,'0', M * M);

                        }
                        pickqueue(num + 1);//下一个皇后
                }
        }
        //遍历完所有列数后都找不到位置，即说明上一个皇后需要重新放置
        if (num==0)//若到退到0列都找不到合适位置，即返回
        {
                return;
        }
        else
        {
                queue[--num]=-1;//上一个皇后列数清除
        }
}
void main()
{
        pickqueue(0);//第一个皇后
        printf("loopcnt:%d\n", loopcnt);
}