【学习笔记】现代循环神经网络

现代循环神经网络

暑假结束，手头上的任务也完成了一部分，终于又可以抽出时间来学习了。前几天学习了下现代循环神经网络学习，主要深入研究了下 LSTM 和 GRU ，其实现在已经很少把这两个模型作为主要的框架去解决实际问题了，但是因为偶尔在预处理时提取文本特征信息的时候会用到，所以还是花了点时间看了下相关内容。另外其实还学习了下注意力机制，但因为那块基本都是数学公式的推导，很难打公式，所以打算直接记Transformer 架构之后的笔记了。

reference :

• https://zh.d2l.ai/
• https://r2rt.com/written-memories-understanding-deriving-and-extending-the-lstm.html#fn11

LSTM 长短期记忆网络

输入输出门

长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。

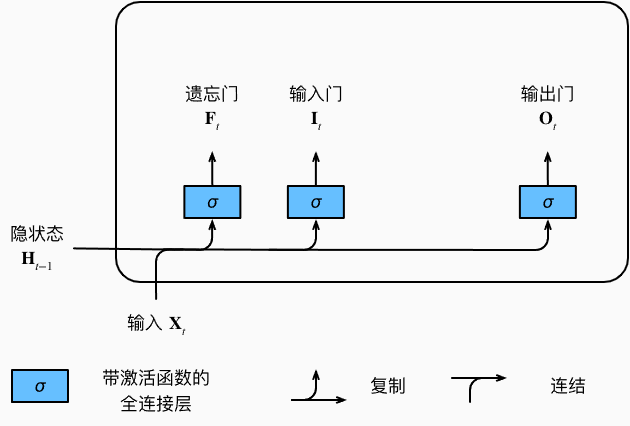
为了控制记忆元，我们需要许多门。 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理， 这种设计的动机与门控循环单元相同， 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。 结构如下所示：

模型输入：当前时间步的输入和前一个时间步的隐状态

假设有ℎ个隐藏单元，批量大小为n，输入数为d。 因此，当前步的输入为$$X_t\in R^{n\ast d}$$， 前一时间步的隐状态为$$H_{t-1}\in R^{n\ast h}$$。 相应地，时间步 t 的门被定义如下： 输入门是$I_t\in R^{n\ast h}$， 遗忘门是$F_t\in R^{n\ast h}$， 输出门是$O_t\in R^{n\ast h}$，激活函数均采用的是 $Sigmoid()$，因此三个门的输出值的范围均为$(0,1)$。
$$\begin{gathered} I_t=\sigma (X_t{W}_{xi}+H_{t-1}{W}_{xi}+b_i) \\ {F}_t=\sigma (X_t{W}_{xf}+H_{t-1}{W}_{xf}+b_i) \\ {O}_t=\sigma (X_t{W}_{xo}+H_{t-1}{W}_{xo}+b_i) \end{gathered}$$
可以通过上述公式计算出各个门的值，同时其中的参数可供学习，且三者的计算方式都是使用了当前步的输入和前一个时间步的隐状态。

候选记忆元

候选记忆元（candidate memory cell）的计算与上面描述的三个门的计算类似，但是使用$tanh$函数作为激活函数，函数的值范围为$(-1,1)$。 下面是在时间步 t处的方程：
$${\tilde{C}}_t=tanh(X_t{W}_{xc}+H_{t-1}{W}_{xc}+b_c)$$
加入后结果如下所示：

记忆元

为了控制输入和遗忘，在长短期记忆网络中，有两个门用于这样的目的： 输入门$I_t$控制采用多少来自${\tilde{C}}_t$的新数据， 而遗忘门$F_t$控制保留多少过去的记忆元 $C_{t-1}\in R^{n\ast h}$ 的内容。
$$C_t=F_t⨀C_{t-1}+I_t⨀{\tilde{C}}_{t-1}$$
如果遗忘门始终为1且输入门始终为0， 则过去的记忆元 $C_{t-1}$ 将随时间被保存并传递到当前时间步。 引入这种设计是为了缓解梯度消失问题， 并更好地捕获序列中的长距离依赖关系。

添加记忆元后的流程图如下所示：

隐状态

除了对记忆更新之外，还需要设置方式对隐状态$H_t$进行更新，这就是输出门发挥作用的地方。 在长短期记忆网络中，它仅仅是记忆元的 tanh 的门控版本。 这就确保了 $H_t$ 的值始终在区间(−1,1)内：
$$H_t=O_t⨀tanh(C_t)$$
只要输出门接近1，我们就能够有效地将所有记忆信息传递给预测部分， 而对于输出门接近0，我们只保留记忆元内的所有信息，而不需要更新隐状态。

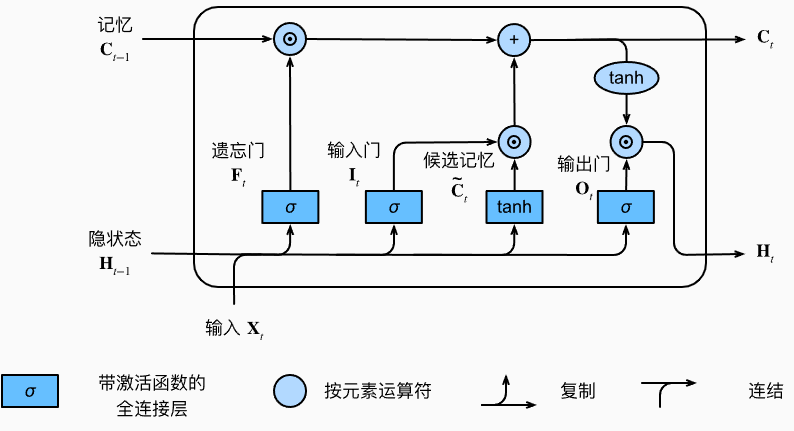
添加隐状态后的结构图如下所示：

总结：长短期记忆网络引入了三个门和一个记忆元，通过遗忘门来控制记忆，使用输入门和候选记忆来更新记忆，通过输出门和记忆来更新隐状态。

代码

'''初始化参数'''
def get_lstm_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xi, W_hi, b_i = three()  # 输入门参数
    W_xf, W_hf, b_f = three()  # 遗忘门参数
    W_xo, W_ho, b_o = three()  # 输出门参数
    W_xc, W_hc, b_c = three()  # 候选记忆元参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
              b_c, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

'''定义模型'''
def init_lstm_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),torch.zeros((batch_size, num_hiddens), device=device))

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)	#输入门
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)	#遗忘门
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)	#输出门
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = (H @ W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, C)
    

GRU 门控神经网络

门控神经网络是 LSTM 的简化版本，通常能够提供同等的效果， 并且它的计算速度相较于更复杂的 LSTM ，有了较大提升。

重置门和更新门

门控神经网络相较于传统的循环神经网络添加了两个门 —— 重置门（reset gate）和更新门（update gate）。我们把它们设计成(0,1)区间中的向量， 这样我们就可以进行凸组合。 重置门允许我们控制“可能还想记住”的过去状态的数量； 更新门将允许我们控制新状态中有多少个是旧状态的副本。

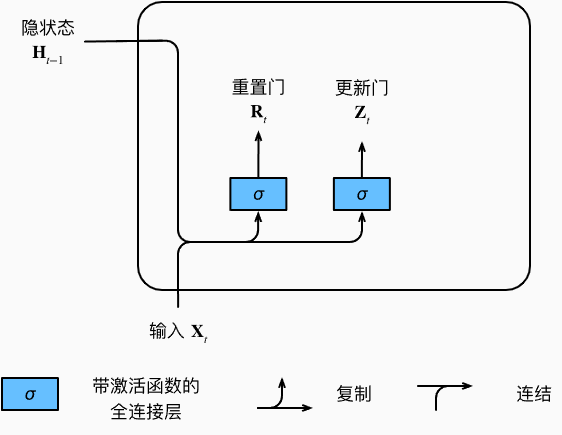
门控神经网络的输入由当前时间步的输入和前一时间步的隐状态给出。 两个门的输出是由使用sigmoid激活函数的两个全连接层给出。两个门的结构图如下所示：

对于给定的时间步 t，假设输入是一个小批量$X_t\in R^{n\ast d}$， 上一个时间步的隐状态是 $H_{t-1}\in R^{n\ast d}$ （隐藏单元个数ℎ）。 那么，重置门 $R_t\in R^{n\ast d}$ 和更新门 $Z_t\in R^{n\ast d}$ 的计算如下所示：
$$\begin{gathered} R_t=\sigma (X_t{W}_{xr}+H_{t-1}{W}_{hr}+b_r) \\ {Z}_t=\sigma (X_t{W}_{xz}+H_{t-1}{W}_{hz}+b_z) \end{gathered}$$

候选隐状态

将重置门 $R_t$ 中的常规隐状态更新机制集成， 得到在时间步 t 的候选隐状态（candidate hidden state）$\tilde{H}=tanh(X_t{W}_{xh}+(R_t⨀H_{t-1})W_{hh}+b_h)$ 。

使用tanh非线性激活函数来确保候选隐状态中的值保持在区间(−1,1)中。 每当重置门$R_t$中的项接近1时， 则恢复成一个普通的循环神经网络。 对于重置门$R_t$中所有接近0的项， 候选隐状态是以$x_t$作为输入的多层感知机的结果。 因此，任何预先存在的隐状态都会被重置为默认值。其计算流程图如下所示：

隐状态

上述的计算结果只是候选隐状态，我们仍然需要结合更新门$Z_t$的效果。 这一步确定新的隐状态$H_t\in R^{n\ast h}$在多大程度上来自旧的状态$H_{t-1}$和新的候选状态${\tilde{H}}_t$。 更新门$Z_t$仅需要在 $H_{t-1}$和 ${\tilde{H}}_t$ 之间进行按元素的凸组合就可以实现这个目标。这就得出了门控循环单元的最终更新公式：
$$H_t=Z_t⨀H_{t-1}+(1-Z_t)⨀{\tilde{H}}_t$$
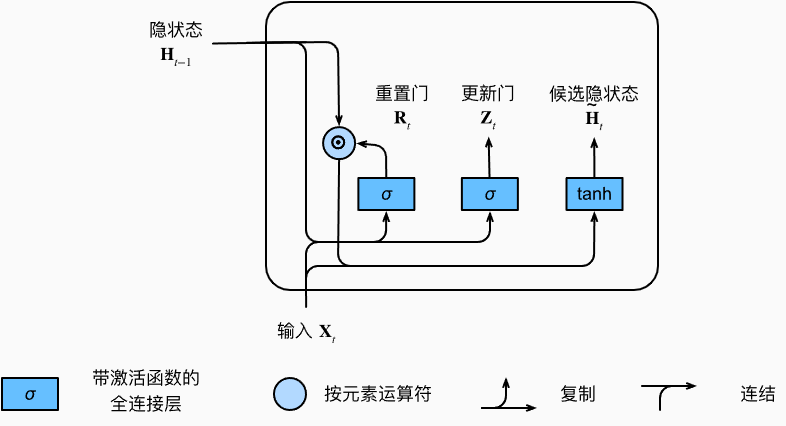
每当更新门$Z_t$接近1时，模型就倾向只保留旧状态。 此时，来自Xt的信息基本上被忽略， 从而有效地跳过了依赖链条中的时间步t。 相反，当Zt接近0时， 新的隐状态Ht就会接近候选隐状态${\tilde{H}}_t$。 这些设计可以帮助我们处理循环神经网络中的梯度消失问题， 并更好地捕获时间步距离很长的序列的依赖关系。 例如，如果整个子序列的所有时间步的更新门都接近于1， 则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。总流程图如下所示：

总结：GRU门控神经网络设置了重置门和更新门，其中重置门的作用是用来生成候选隐状态，更新门的作用用于判断是否加入候选隐状态的影响。

代码

'''初始化参数'''
def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xz, W_hz, b_z = three()  # 更新门参数
    W_xr, W_hr, b_r = three()  # 重置门参数
    W_xh, W_hh, b_h = three()  # 候选隐状态参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

'''定义模型'''
def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)	#更新门
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)	#重置门
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)	#候选隐状态
        H = Z * H + (1 - Z) * H_tilda						#更新隐状态
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

深度循环神经网络

过去的循环神经网络都只具有一个单向隐藏层的循环神经网络。隐变量和观测值与具体的函数形式的交互方式是相当随意的。

我们将多层循环神经网络堆叠在一起， 通过对几个简单层的组合，产生了一个灵活的机制。 特别是，数据可能与不同层的堆叠有关。

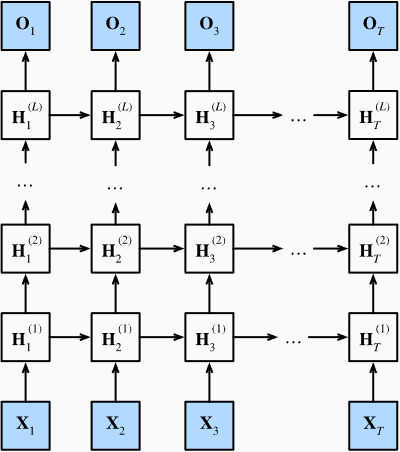
下图描述了一个具有 L 个隐藏层的深度循环神经网络， 每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。

假设在时间步 t 有一个小批量的输入数据$X_t\in R^{n\ast d}$，同时，将$l^{th}$隐藏层（$l=1,\dots ,L$） 的隐状态设为$H^{(l)}\in R^{n\ast h}$（隐藏单元数：ℎ）， 输出层变量设为$O_t\in R^{(n\ast q)}$（输出数：q）。 设置$H_i^{(0)}=X_t$， 第 l 个隐藏层的隐状态使用激活函数$\Theta (l)$，则：
$$H_t^{(l)}={\Theta }_l(H_t^{(l-1)}{W}_{xh}^l+H_{t-1}^l{W}_{hh}^l+b_h^l)$$
最后，输出层的计算仅基于第 $l$ 个隐藏层最终的隐状态：
$$O_t=H_t^{(L)}{W}_{hq}+b_q$$

代码实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)

Next

其实除了深度循环神经网络之外还有双向循环神经网络，但是因为新一点的 task 都已经开始采用 Transfomer 架构，所以不打算对这部分进行深入学习了。

下周组会要分享 transformer ，本周应该会做一个比较详细的关于 transformer 的笔记。之前计划暑假学完基础，还是太天真了hhhh。事情真的太多了==
计划本周弄完 transformer，下周能看完 Bert、GPT、Vit，9 月中旬看完多模态基础部分，之后再去多关注下顶刊和顶会上 fansy 点的工作吧！

Fighting ！