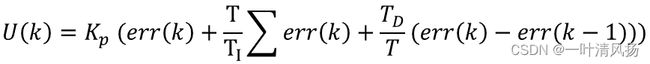PID控制

1 基本情况

1.1 位置式PID

（1）基本的连续PID控制
公式：

（2）离散PID控制
将连续的进行离散化。表述。

1.2 增量式PID

（1）公式推到过程
（a）k-1时刻的离散表示：

（b）利用U(k) - U(K-1)，得到本次的增量：

（c）控制的输出是增量式的，就是deltUk。
（2）说明
（a）增量式PID的输出是增量，不是累加的。即为deltUk，而不是Uk
（b）在有的地方，提到了输出是U(k) = U(k) - U(k-1)，这个本质上也是位置式的，只是计算过程不一样而已！！！
( c) 如果要使用增量式，因为只输出增量，所以要求控制系统自己能够保持之前的输出效果，而不需要之前的量来累积。也就是有点地方说的机构具有积分作用。如步进电机。这有点像无PD控制了。
（d）其只依赖于最近三次的数据，就能计算计算量小，对误差容忍小等。
最最重要的：
（e）增量式的PID的参数值虽然也叫PID，但是与位置式PID的PID的意义不同！！ 具体说，在增量式中：I是比例，P是微分，D是二阶微分（微分的微分）。
（f）因此，后面讲的很多涉及积分调整和控制的不涉及这里。
（g）后面说的比例对应这里的I，微分控制对应这里的P，输出类似。
（h）位置PID整定的方法，在增量式整定时使用其思想，不能简单的将PID进行对应！

1.3 PID控制适用系统

虽然PID控制在实际控制中有非常多的应用，据说在工业上，达到95%以上应用。但是它也是有适用范围的，不是包打天下的。
它适用于线性系统，准确未二阶以内线性系统。
所谓二阶线性系统，需要满足两个特性：
（1）齐次性。要求：y = f(x)，则ky = f（kx）
（2）叠加性。要求：y1 = f(x1)，y2 = f(x2)，则有y1 + y2 = f(x1) + f(x2)。

不适用系统包括：
（1）高阶线性系统。
如果高阶系统可以简化为二阶系统，则可以用PID控制。
（2）非线性系统。
这个可以用李雅普诺夫方法，在非线性系统的平衡点处，进行转化为线性后应用。具体可以参见这里的介绍：https://zhuanlan.zhihu.com/p/58738073

2 PID三个量的含义解析

重要说明：下面章节说的PID针对位置型PID说的。增量式的参照执行：
（1）下面章节的P比例对应增量的I。
（2）下面章节涉及到的D微分对应P。
（3）下面章节涉及到的输出，增量式的输出可参照执行。

2.1 P：比例

（1）他当前的输出只与当前偏差有关系，与历史没有关系。
（2）只要有偏差，该输出就存在。没有了偏差，就没有输出。
（3）他的输出值与偏差值是一个线性关系。
（4）从大的偏差开始控制，随着控制的时间拉长，偏差值越来越小，他的输出也会越来越小。（当然，接近控制值后，可能会有震荡的情况除外）。如下图示意所示：

（5）注意上图中，输出跟偏差是线性关系，但是跟时间不是线性关系。因为P的输出越大，则偏差较少越快，对应P的减少越快，到最后，在趋近设置值时会越来越缓慢。

2.2 I：积分

（1）他的输出是历史上所有偏差的累积。如果是离散PID的话就是历史偏差累加。
（2）他不仅与当前偏差有关系，也与历史偏差有关系。因此，即使当前偏差为0，他也会有输出。
（3）积分的引入，是由于某种阻力的存在。来达到以下两个目的：
（a）积分的作用，是为了抵抗某种阻力，保持当前积累的效果。
是把历史上所有的误差进行了累计，所以即使当前没有了误差，他也会有输出，这个输出会保持住当前状态，以抵抗某种阻力。例如：旋翼无人机的持续旋转，抵消重力，实现空中某个位置的悬停。
因此，一般，需要抵消某种阻力存在时，必须需要积分的存在，I是不能少的。
（b）积分的作用，是为了解决稳态误差（也有叫做静态误差的）。
如上面说的那样，有某种外面阻力存在的话，如果只靠P调节的话，会导致P无论怎么调，都会存在以下情况：最后进入稳态后，与设置值，之间会有一个稳定的误差，称为稳态误差。
这个就需要通过积分，将其消除掉。
（4）从大的偏差开始控制，随着控制的时间拉长，偏差值越来越小，他的输出也会越来越小。直到为0（当然，这里假设没有考虑震荡情况，按照特列，直接到0，实际这是不太可能的。只是示意一下）。如下图示意所示：

（5）从上图可以看出，输出一直在增大的，但是随着时间拉长，偏差越来越小，其累积的值也越来越小，最后称为定值（偏差为0）.。当然，这种情况是理想的，因为往往会超调，超调后，方向相反，则累加和会变小。后续的图就没办法用这个图表示了，这里没有表示。可以同样逻辑分析。
（6）积分的副作用
积分会带来很多的辅作用，比如积分饱和、积分意外累积，对变化影响不利等。详见3章中相关章节。

2.3 D：微分

（1）输出与偏差的变化有关系，如果偏差一直保持不变，则D没有输出；
（2）这个输出的结果阻尼，是要抵消PI的输出结果，使其不至于让他们的输出变化太快。
（3）这个阻尼有两种结果：
（a）当PI的输出促使偏差减小，向设置值靠拢时，微分会阻止这种靠拢。如果D值设计合理，这种阻尼是阻止其较快的到达，提前刹车，防止过充引起超调震荡；
（b）当PI的输出，过充后，促使偏差减大时，微分也会阻止这种变大，设置合理，能够将其拉回到设置点。
（4）D实现这种阻尼的方式是基于预测的方式来实现的，预测的方式是将过去的偏差变化，认为是下面也会有的变化。将这个变化结果作为预测结果，提前减少输出。
（5）D的副作用。
（a）如果D太小，则起不到较好的阻尼效果，会使震荡收敛时间长；
（b）如果D值设置太大，则会使得微分阻尼过调，引起高频震荡。设置无法收敛。
（c）D的出现，使得系统对噪声、干扰、变化（如设置值变化）特别敏感，因为噪声和干扰的出现会使得偏差出现剧烈变化，从而导致系统出现高频震荡，或者无法快速收敛。解决方法：低通滤波器，微分先行等，详见3.6，3.7。

2.4 PID：三者的关系

（1）PI关系。
（a）从上面的图中可以看出，从开始控制到偏移量逐渐缩小到偏差为0的过程中，二者是一个P输出逐渐减小，I输出逐渐增大过程。理想情况偏差为0时，二者的输出，最好能保持一个抵消阻力的情况，这样正好能够平衡稳定。
（b）但是以上所说的情况，由于起始点不同，每次积分累积的输出也不同，在偏差为0时，所以往往有超调，这就引起了震荡。
（c）上述情况的一个特例，就是如果没有外力时，应该没有I，此时输出为0。此时虽然没有了输出，但是由于延迟输出及系统的惯性，所以也会有震荡。
（2）PID关系，上面的情况，往往会引起震荡，此时D能阻尼、对冲这种过调。

3 PID控制中特殊情况考虑

上面介绍了最基本的PID控制情况，实际在控制中会遇到很多特殊情况，包括：
（1）意外偶发阻力干扰；
（2）启动停止时控制；
（3）大范围的误差控制；
（4）单向误差累积。
还需要再基本的PID控制中引入其他辅助或变换的做法。

3.1 积分限幅

（1）针对问题：
在开始控制后，有一个较大误差，且有一个非常大干扰的话，例如外界阻力，阻止其误差减小，如上面说的旋翼飞机被人死死的按住。虽然他的PI都在输出，但是误差一直没变。这时候，随着时间的拉长，积分的输出值会越来越大。如下图所示：

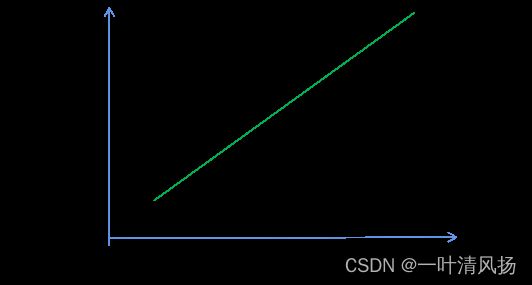
这将导致以下问题：
（a）这种输出可能超过了控制系统承受范围
（b）而一旦这种阻力去掉，会使得这种输出很大很大，引起很大的超调和震荡。
（2）解决方法
引入积分限幅。原理给定一个积分输出的最大值限制，一旦超出，则不再增加。
上述被意外阻挡情况下的输出图如下图所示：

这个在这里有介绍：https://www.bilibili.com/video/BV1B54y1V7hp?p=4

3.2 积分分离

（1）针对问题
在大幅度增减设定值，或者控制启动、结束过程中，短时间内会有很大偏差。而积分由于会累积这种误差，造成后面都持续偏大，会使得整个过程中的输出过大，从而引起超调和震荡。
（2）解决方法
引入了积分分离的思想。其思路是::
（a）偏差值较大时，取消积分作用，以免于超调量增大。实际上利用PD进行控制。
（b）偏差值较小时，引入积分作用，以便消除静差，提高控制精度。利用PID进行控制。

问题关键是如何选择这个偏差阈值。
详见：https://blog.csdn.net/foxclever/article/details/80274790
在这里有介绍：https://www.bilibili.com/video/BV1B54y1V7hp?p=4

3.3 积分饱和

（1）针对问题
如果一个系统总是存在统一个方向的偏差，就可能无限累加为一个很大的输出，称为饱和。饱和后，如果此时又有一个反向的偏差，会使得这个反向误差首先抵消饱和部分，然后才能响应反向偏差。从而影响系统收敛的性能。
（2） 解决方法
引入了抗积分饱和的PID算法。所谓抗积分饱和算法，其思路是在计算U(k)的时候，先判断上一时刻的控制量U(k-1)是否已经超出了限制范围。若U(k-1)>Umax，则只累加负偏差；若U(k-1) 具体参见：https://blog.csdn.net/foxclever/article/details/80294264

3.4 梯形积分

从微积分的基本原理看，积分的实现是在无限细分的情况下进行的矩形加和计算。但是在离散状态下，时间间隔已经足够大，矩形积分在某些时候显得精度要低了一些，于是梯形积分被提出来以提升积分精度。

https://blog.csdn.net/foxclever/article/details/80297989

3.5 变积分PID

积分的系数分段，误差越大时I越小，误差越小时，I越大。
类似于积分分离，积分分离应该是这个的一个特例。具体参见：https://blog.csdn.net/foxclever/article/details/80466623

3.6 不完全微分PID

微分信号的引入可改善系统的动态特性，但也存在一个问题，那就是容易引进高频干扰，在偏差扰动突变时尤其显出微分项的不足。为了解决这个问题人们引入低通滤波方式来解决这一问题。
微分项有引入高频干扰的风险，但若在控制算法中加入低通滤波器，则可使系统性能得到改善。方法之一就是在PID算法中加入一个一阶低通滤波器。即高频降低通过，低频通过。
详细见：https://blog.csdn.net/foxclever/article/details/80551919

实现时，只对D加了一个一阶低通滤波：
d * (1 - alpha) * (Ek - Ek-1) + alphaEk-1。

3.7 微分先行

针对频繁切换设定值时，微分会有干扰，不稳定。因此，改进为不对偏差取微分，而是对输出值取微分。
详见：https://blog.csdn.net/foxclever/article/details/80633275

3.8 死区PID

在计算机控制系统中，由于系统特性和计算精度等问题，致使系统偏差总是存在，系统总是频繁动作不能稳定。为了解决这种情况，我们可以引入带死区的PID算法。带死区的PID控制算法就是检测偏差值，若是偏差值达到一定程度，就进行调节。若是偏差值较小，就认为没有偏差.
https://blog.csdn.net/foxclever/article/details/80778748

3.9 模糊PID

在PID的基础上，增加一个PID的变化值。
这个变化值与偏差的范围和大小建立一个关系。
https://blog.csdn.net/foxclever/article/details/83932107

3.10 步进PID

（1）针对问题：
当设置值突然大幅变化时，会造成微分项产生较大的输出，当然这个可以使用微分先行的方式解决；但是同时比例输出也会有大的变化，当然我们可以利用比例先行，但这样会破坏原来的PID控制，带来别的问题。
（2）解决方法
采用步进式的方式设置设定值，就是通过分几步增加设置值，逐步到最终的设定值。
详见：https://blog.csdn.net/foxclever/article/details/105747647

3.11 使用带时间的PID

简化的PID中是已经包含了时间的，且这个时间间隔是相等的，如果不相等，则可能需要引入原来的时间运算。
这里有介绍：
https://blog.csdn.net/foxclever/article/details/122801130

3.12 其他

还有不少控制的，可以参看这里：https://blog.csdn.net/foxclever/category_9281151.html

4 位置型PID中如何使用与调节PID的值

4.1 如何使用

实际使用时，PID可能不是都使用的，有：
（1）PI，D=0
有自然的阻尼的情况。如水中弹簧震荡，水有阻尼，或者阻尼能够较好的平衡掉该中情况下PI的震荡。

（2）PD，I=0
没有外界阻力情况，物理机械能够保证自平衡。
比如在水平面上小车控制运动到指定位置，且这个小车电机等没有阻力，到位置后不需要再输出就可以保持。

（3）PID，比较常见的

（4）PIDT，也用上了T
如上面3.11中，就需要考虑将T，也加入了。

4.2 如何调整PID参数值

（1）先调P
从小到大，依次增加调节。
那么增加到什么情况合适呢，考虑两个因素：
（a）最大误差情况下，是否能够达到设定值
（b）最大误差情况下，达到设定值的时间
上面两个因素，都是考虑最大误差情况下。这个最大误差根据控制对象，有的有明显的边界，如果没有明显边界，则应该考虑先定一个边界，在边界之外使用固定的输出，或者使用固定的P来输出，类似于积分限界、防过饱和的情况。在边界之内再进行精确调节。
这两个因素考虑时，（a）主要在有明显的外界阻力需要抵抗，则如果P小的时候，是否无法达到设定的值的，需要调节P到达设定值，可以适当超调一些。让其震荡得到。
（b）主要是看效率，在有外力需要抵消情况下看，还要看时间。没有外力时，虽然一直可以达到，但是要考虑时间。

综合考虑一下上面，两种情况后，确定P。

（2）第二个调节I的情况
如果认为D影响较小的情况下。可以先调节这个。

（3）第二个调节D的情况
以下情况可以使用第二个调节D：
（a）如果认为I较小的情况
（b）调节P后有较大低频震荡，需要先把震荡调节下来。
在进行了PD调节后，发现有静态误差，则调节一下I，补充进入。

5 增量型PID中参数整定

第4章说的PID针对位置型PID说的，增量式的参照执行：
（1）下面章节的P比例对应增量的I。
（2）下面章节涉及到的D微分对应P。
（3）下面章节涉及到的输出，增量式的输出可参照执行。

因此，增量型PID参数整定过程如下：
（1）先调节I，P=0，D=0。I从小到达，这个过程中会有如下过程：
（a）能够收敛，但是收敛速度太慢！
（b）稳定加快，出现震荡趋势，并趋势逐渐明显
（c）有震荡，震荡的幅度在逐渐减小，收敛
（d）振幅增大，收敛时间过长，甚至无法收敛，
上述过程中，选c那个参数。
（2）在步骤1基础上（I已经选取了上面步骤c的值），D=0，调节P，从小到大，经历以下过程：
（a）对上面的震荡效果没有影响，影响逐渐出现，振幅减小，收敛加快
（b）有较好的振幅减小，收敛效果
（c）新的震荡出现，更加不稳定
上述过程中，选b步骤的值给I
（3）在步骤2基础上，选取P、I值，然后调节D，从小到大，经历如下过程：
（a）对上面的震荡效果没有影响，影响逐渐出现，振幅减小，收敛加快
（b）有较好的振幅减小，收敛效果
（c）新的震荡出现，更加不稳定
上述过程中，选b步骤的值给D。
（4）PID关联、精细化调节
上面已经初步调节好了PID，确定了他们的量级。由于PID是相关联的，且还需要处理很多特殊情况，做多的实验，所以，还需要再精细的调节。

这里可以参考一个其他人做的实验过程，更加形象直观：
狂暴战车 直流电机转速闭环，增量式pid调试过程

5 参考文献

【1】这里有比较抽象的介绍：https://blog.csdn.net/foxclever/article/details/80250994
【2】其中很多出自这个英文的网站，可以查看这里：http://brettbeauregard.com/blog/2011/04/improving-the-beginner%e2%80%99s-pid-derivative-kick/
【3】关于PID，这里有一个较好的解释: PID算法原理 一图看懂PID的三个参数
【4】同样，这里有视频课程介绍。
【5】狂暴战车 直流电机转速闭环，增量式pid调试过程