python数据分析(Jupyter Notebook工具)之numpy库
数据分析是一门借助于计算机系统,针对海量、结构各异、不规则的数据进行高效处理,从中间提取对科学、技术、经济、社会有用的信息,并对人类的各种活动产生有益的指导作用。
数据分析领域涉及的主要技术包括数据加载、数据转换、数据查询、数据聚合、数据拆分、数据可视化等,由三个核心包实现: NumPy、 Pandas 和 Matplotlib。 NumPy 实现高效的复杂数学运算,为包括数学分析在内的科学计算提供强大的计算平台; Pandas 提供了数据分析中涉及的主要前端功能,如数据加载、数据转换、数据查询、数据聚合与拆分等;Matplotlib 为快速展现数据分析成果提供了一个功能强大的工具集。
目录
数组操作
数组特性
广播机制
数组基本操作
查询数组
排序数组
数组操作
熟悉 NumPy 的首要任务为熟悉数组的创建。
1,arange()方法创建一维数组,注意: arange(10)创建的数组里面不包括元素 10
2.创建指定步长的一维数组,arrange(10,100,30)中的参数 10、 100、 30 分别为起始值、终止值、步长,即创建的数组里 面包括 10、 40( 10+30)、 70(40+30),但不包括 100。
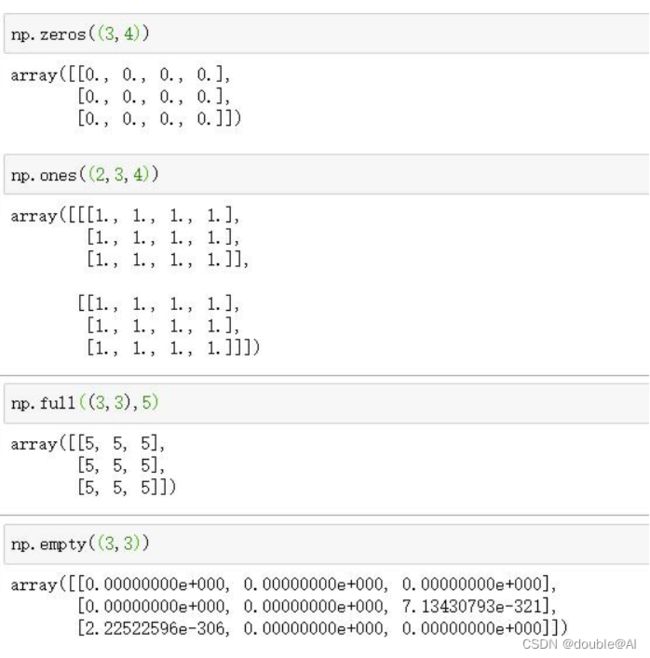
3.使用 zeros()和 ones()创建一维数组
4. 使用 empty()和 full()创建一维数组, empty()使用随机数填充新创 建的数组
5.使用 linspace()和 random()创建一维数组
linspace(0,10,5)返回区间 0~10 内均匀间隔的 5 个数字,即 0、 2.5、 5、 7.5、 10
6.使用 zeros()、 ones()、 full()和 empty()创建多维数组
7.使用 arange()创建多维数组
先使用 arange(24)生成包含 24 个元素的一维数组,再调用 reshape()将其转换为 一个 3 维数组,每个维度的元素个数分别为 2、 3、 4。
数组特性
1.查看数组的数据类型
2. 创建指定数据类型的数组
3.查看数组的形状
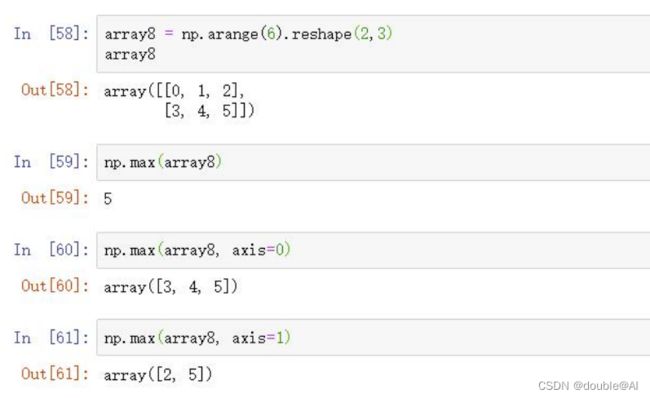
4.使用不同轴向参数调用 max()
作为 一个支持各类科学计算的基础包, NumPy 存储和处理的数据大都为多维数组,而同一个操作 在多维数组上可能具有多种不同的操作方向,因此 NumPy 引入轴向概念,指示操作的方向。 一维数组只有一个轴向( Axis=0),二维数组有两个轴向,分别为 Axis=0(垂直轴向)和Axis=1(水平轴向),三维或以上数组以此类推。
广播机制
不同大小的数组不能进行加、减,或通常的算术运算。但是,实际项目中经常会需要对大 小不同的数据进行处理和运算,因此 NumPy 引入广播机制(Broadcasting),用于解决不同大 小数组之间的算术运算问题。广播机制的原理为适当“扩大”数组的形状,使得两个数组的形 状完全相等。
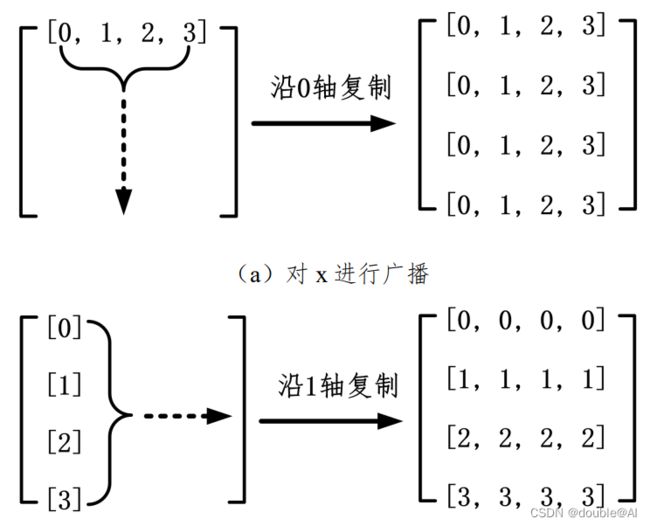
为解决不同形状数组之间的算术计算问题,广播对数组进行变换,从而实现形状不同的数 组之间也能进行算数计算。广播的核心原理为按照一定的规则对数组进行扩展和复制,从而使 多个数组的形状保持一致,其主要步骤如下所述:
( 1) 扩展:如果数组维数不同,则扩展维数少的数组,在其形状中添加前缀 1,使 其维数与最多维数数组的维数相等。例如,如果 x.shape=(2,), y.shape=(7,2,3),则扩展 x 的维数: x.shape=(1,1,2)。
(2) 复制:如果某一轴向的长度为 1,则沿此轴向复制此轴向上唯一的数据,使其 长度与所有数组在此轴向上的最大长度相等。需要说明的是 NumPy 并没有进行真正的复制操 作,而是通过指针来模拟复制操作。另外,如果多个数组在某个轴向上的长度不相等并且不为1,则复制失败。
(3) 计算:执行完广播后的数组均具有相同的形状,因此可以进行相应的算术计算。
例:x=np.arange(4).reshape(1,4)
y=np.arange(4).reshape(4,1)
z = x + y
则z = [[0,1,2,3],[1,2,3,4],[2,3,4,5],[3,4,5,6]]
数组基本操作
1.使用 reshape()变换数组形状
2.拼接数组
3.切分数组
4.访问数组(利用整数索引和切片索引访问一维数组)
x[3]:首先获取结果集,即访问 x 中第 3 个元素,因此结果集为 [3]。因为本例中使用 标量索引来访问 0 轴数据,参考表 2-4,得知变换后的结果集形状为 (,),即需将结果集形状变 换为标量,因此最后返回标量 3。
x[2:5]:访问 x 中第 2 个到第 4 个之间的元素(不包括终止值 5),结果集为 [2, 3,4]。 0 轴使用切片索引,因此 0 轴形状为切片索引的数值个数,即 3,将结果集的形状转换为(3,),最后返回 [2, 3, 4]。
x[:5]:访问 x 中第 0 个到第 5 个之间的元素,输出为 [0, 1, 2, 3, 4]。 NumPy 采用 与 Python 中切片相同的处理方式,省略切片中的开始值表示从第 0 个元素开始。结果形状的 确定与 x[2:5]相同,不再赘述,以下同。
x[7:]:访问 x 中第 7 个到最后一个元素,输出为 [7, 8, 9]。省略切片中的终止值表示 一直到最后一个元素。
x[5::-1]:倒序访问第 5 个到第 0 个元素,输出为 [5, 4, 3, 2, 1, 0]。指定步长为 -1
表示倒序访问数组元素。
5.利用整数索引和切片索引访问二维数组
y[2,1]: 0 轴索引和 1 轴索引均为标量索引,即访问 y 中第 2 行第 1 列的数据,结果集 为 [9]。
y[1]: 0 轴索引为标量, 1 轴没有指定索引,即访问第 1 行所有列的数据,结果集为
[4,5,6,7]。
y[:2,2:3]:访问 y 中的第 0 行至第 1 行中的第 2 列至第 2 列的数据,结果集为 [2,6]。 0
轴和 1 轴均指定了切片索引,且分别包括 2 个和 1 个数值,因此最终形状为 (2,1),即返回
[[2],[6]]。
y[:,0]:访问所有行的第 0 列数据,最终输出结果为 [0,4,8]。
查询数组
数据处理与分析中存在大量的查询操作,如查询 7 月平均气温高于 30 摄氏度的城市,销 售额最高的年份,高于平均成绩的人数等。 NumPy 提供 where()、 extract()、 all()、 any()支持基 于条件的查询,提供 amin()、 amax()、 median()、 mean()等方法支持各类统计计算。
all()和 any()用来按轴向检测数据是否全部为真值或者存在至少一个真值。
NumPy 中常用的统计方法列表
统计方法的使用如下:
排序数组
NumPy 提供了一系列适应于数组的排序方法,包括 sort()、 argsort()、 lexsort()、 partition()、sorted()等。
主要排序方法列表
下面代码演示了 NumPy 中常见排序算法的使用:
小结:
作为一个支持数据分析与科学计算的基础包, NumPy 提供了一个 ndarray 数组结构,克服 了 Python 内置的 List 结构对于多维数组支持的局限性,提升了多维数据存储、访问、操作的 效率。以数组为基础, NumPy 为数据访问、形状变换、数据访问、数据计算提供了丰富的功 能支持与方法实现,成为常见的科学计算、数据分析、机器学习包的后台基础包。如果没有NumPy, Python 在数据分析、科学计算、人工智能方面的应用前景会受到不可估量的影响。因 此,了解和熟悉 NumPy 将为数据分析提供理论与实践基础,使数据分析工作者对于数据分析 操作不仅知其然,而且知其所以然。