Adversarial Attacks and Defenses on Graphs: A Review, A Tool and Empirical Studies(2020)
Adversarial Attacks and Defenses on Graphs: A Review, A Tool and Empirical Studies----《图上的对抗性攻击和防御:回顾、工具和实证研究》
摘要
深度神经网络(DNN)在各种任务中都取得了显着的性能。然而,最近的研究表明,DNN 很容易被输入的小扰动所欺骗,称为对抗性攻击。作为 DNN 对图的扩展,图神经网络(GNN)已被证明继承了该漏洞。对手可以通过修改图结构(例如操纵一些边)来误导 GNN 给出错误的预测。这一漏洞引起了人们对在安全关键型应用中采用 GNN 的极大关注,并且近年来吸引了越来越多的研究关注。因此,有必要且及时地全面概述现有的图对抗攻击及其对策。在本次调查中,我们对现有的攻击和防御进行了分类,并回顾了相应的最先进方法。此外,我们还开发了一个具有代表性算法的资源库。该存储库使我们能够进行实证研究,以加深我们对图的攻击和防御的理解。
引言
图可以用来表示跨不同领域的大量系统,如社会科学(社会网络)、自然科学(物理系统和蛋白质相互作用网络)和知识图[2;26]。随着图的普遍存在,学习有效的图表示方法具有重要意义,它可以促进节点分类、图分类、链接预测和推荐等下游任务的完成[2;26]。图神经网络(gnn)将传统的深度神经网络(dnn)推广到图中,为学习图的表示形式提供了一种有效的方法[26;73;3;84]。gnn的强大之处在于它能够同时捕获图的结构和节点特征。除了单独考虑实例(节点及其特性)之外,gnn还利用了它们之间的关系。具体来说,GNN 遵循消息传递方案 [24],其中节点聚合并转换来自每层邻居的信息。通过堆叠多个 GNN 层,信息可以通过图结构进一步传播,并且我们可以将节点嵌入到低维表示中。然后,可以将获得的节点表示输入到任何可微的预测层中,以便可以以端到端的方式训练整个模型。由于其强大的表示学习能力,GNN 在数据挖掘等各种应用中都获得了实际意义[34; 63],如自然语言处理[48]、计算机视觉[37]、医疗保健和生物学[45]。
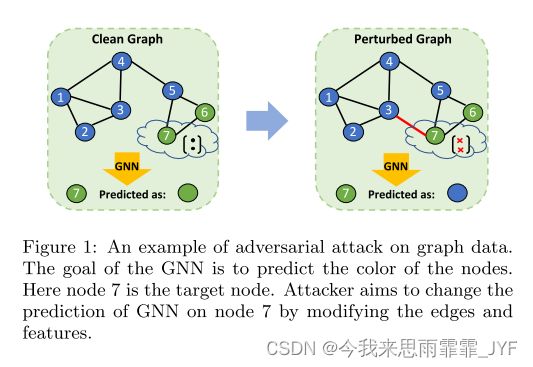
作为传统 DNN 对图的新推广,GNN 继承了传统 DNN 的优点和缺点。与传统的 DNN 类似,GNN 在学习图表示方面也很强大,并且已经渗透到许多科学技术领域。传统的 DNN 很容易被对抗性攻击所愚弄 [25; 75; 40; 39]。换句话说,攻击者可以在训练或测试阶段加入轻微的扰动,DNN 模型将完全失败。显然,GNN 也继承了这个缺点 [89; 17; 91]。攻击者可以通过操纵图结构或节点特征来生成图对抗性扰动来欺骗 GNN 模型。如图1所示,节点7最初被GNN模型分类为绿色节点;在节点 7 与节点 3 创建新连接并修改其自身特征后,GNN 模型将其错误分类为蓝色节点。GNN 的这种脆弱性在金融系统和风险管理等安全关键应用中的应用引起了极大的关注。例如,在信用评分系统中,欺诈者可以伪造与多个高信用客户的联系,以逃避欺诈检测模型;垃圾邮件发送者可以轻松创建虚假关注者,以增加虚假新闻被推荐和传播的机会。因此,迫切需要研究图对抗攻击及其应对策略。
推动这项研究具有促进 GNN 在更广泛领域成功采用的巨大潜力,这促使近年来人们越来越关注图对抗性攻击和防御。因此,有必要且及时地对现有算法进行全面、系统的概述。同时,通过实证研究加深我们对图对抗攻击的理解也具有重要意义。这些理解不仅可以提供有关攻击行为的知识,还可以为我们设计防御策略提供见解。本次调查的主要目的如下:
- 我们在第 3 节中从不同角度对现有的攻击方法进行分类,并在第 4 节中回顾代表性算法。
- 我们根据防御策略对现有对策进行分类,并在第 5 节中对每个类别的代表性算法进行回顾。
- 我们根据我们开发的存储库进行实证研究,该存储库提供了第 6 节中对图攻击和防御的全面理解。
- 我们在第 7 节中讨论了一些有前景的未来研究方向。
预备知识和定义
在进行综述和实证研究之前,我们首先介绍本节中的概念、符号和定义。
图数据学习
在本次调查中,我们使用 G = ( V , E ) G = (V,E) G=(V,E) 来表示图的结构,其中 V = { v 1 , . . . , v N } V = \{ {v_1},...,{v_N}\} V={v1,...,vN} 是 N N N 个节点的集合, E = { e 1 , . . . , e K } E = \{ {e_1},...,{e_K}\} E={e1,...,eK} 是边集。我们用矩阵 A ∈ { 0 , 1 } N × N A \in {\{ 0,1\} ^{N \times N}} A∈{0,1}N×N 来表示 G G G 的邻接矩阵,其中 A i j = 1 {A_{ij}} = 1 Aij=1 表示节点 v i {v_i} vi 和 v j {v_j} vj 在 G G G 中相连。此外,我们使用 X ∈ R N × D X \in {R^{N \times D}} X∈RN×D 来表示节点属性矩阵,其中 D D D 是节点特征向量的维度。因此,图数据可以表示为 G = ( A , X ) G = (A,X) G=(A,X)。图上有很多学习任务,在这项工作中,我们重点关注图上的分类问题。此外,我们使用 f θ {f_\theta } fθ 和参数 θ \theta θ 来表示学习模型。
节点级分类 对于节点级分类,图 G G G 中的每个节点都属于标签集 Y Y Y 中的一个类。图模型旨在学习一个神经网络,基于标记节点(训练节点)(记为 V L {V_L} VL)来预测未标记节点(测试节点)的类别。训练目标函数可以表示为:
min θ L t r a i n ( f θ ( G ) ) = ∑ v i ∈ V L l ( f θ ( X , A ) i , y i ) {\mathop {\min }\limits_\theta {L_{train}}({f_\theta }(G)) = \sum\limits_{{v_i} \in {V_L}} {l({f_\theta }{{(X,A)}_i},{y_i})}} θminLtrain(fθ(G))=vi∈VL∑l(fθ(X,A)i,yi)
其中 f θ ( X , A ) i {{{f_\theta }{{(X,A)}_i}}} fθ(X,A)i 和 y i {{{y_i}}} yi 是节点 v i {{{v_i}}} vi 的预测标签和真实标签, l ( ⋅ , ⋅ ) {l( \cdot , \cdot )} l(⋅,⋅) 是损失函数,例如交叉熵。
图级分类 对于图级分类,每个单独的图在标签集 Y Y Y 中都有一个类。我们用 G G G 表示一组图, G L {G_L} GL 是 G G G 的标记集(训练集)。图级分类的目标是学习映射函数 f θ : G → Y {f_\theta }:G \to Y fθ:G→Y 来预测未标记图的标签。与节点级分类类似,目标函数可以表示为:
min θ L t r a i n ( G ) = ∑ G i ∈ G L l ( f θ ( G i ) , y i ) \mathop {\min }\limits_\theta {L_{train}}(G) = \sum\limits_{{G_i} \in {G_L}} {l({f_\theta }({G_i}),{y_i})} θminLtrain(G)=Gi∈GL∑l(fθ(Gi),yi)
其中 G i {G_i} Gi 是带有真相标签 y i {y_i} yi 的标记图, f θ ( G i ) {f_\theta }({G_i}) fθ(Gi) 是图 G i {G_i} Gi 的预测。
图对抗攻击的一般形式
基于2.1节中的目标,我们可以定义对抗性攻击目标的一般形式,其目的是通过最小化一些攻击损失来误导受害者模型。因此,节点级图对抗攻击的问题可以表述为:
给定 G = ( A , X ) G = (A,X) G=(A,X) 和受害者节点子集 V t ⊆ V {V_t} \subseteq V Vt⊆V。攻击者的目标是找到一个扰动图 G ^ = ( A ^ , X ^ ) {\hat G = (\hat A,\hat X)} G^=(A^,X^) 来最小化以下攻击目标 L a t k {L_{atk}} Latk,
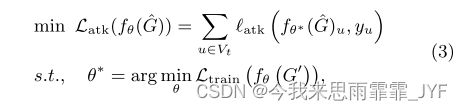
其中 l a t k {l_{atk}} latk 是攻击的损失函数,一种选择是选择 l a t k = − l {l_{atk}} = - l latk=−l 且 G ′ G' G′ 可以是 G G G 或 G ^ \hat G G^ 。请注意, G ^ \hat G G^ 是从约束域 Φ ( G ) \Phi (G) Φ(G) 中选择的。给定固定的扰动预算 Δ,典型的 Φ ( G ) \Phi (G) Φ(G) 可以实现为:
∥ A ^ − A ∥ 0 + ∥ X ^ − X ∥ 0 ≤ Δ {\left\| {\hat A - A} \right\|_0} + {\left\| {\hat X - X} \right\|_0} \le \Delta A^−A 0+ X^−X 0≤Δ
我们省略了图级对抗性攻击的定义,因为(1)图级对抗性攻击可以类似地定义,(2)大多数对抗性攻击和防御都集中在节点级。尽管对抗性攻击已经在图像领域得到了广泛的研究,但由于独特的挑战,我们仍然需要对图进行专门的研究—— (1) 图结构是离散的; (2)图中的节点不独立; (3)难以衡量图上的扰动是否难以察觉。
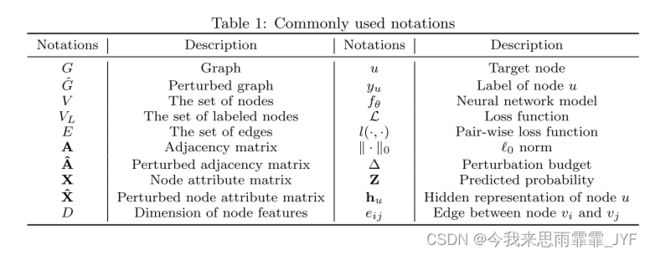
注:根据上述定义,我们在表 1 中列出了以下各节中将使用的所有符号。
图对抗性攻击的分类
在本节中,我们简要介绍图结构化数据的对抗性攻击的主要分类。根据攻击者的目标、资源、知识和能力的不同,攻击算法可以分为不同的类型。我们试图对图对抗攻击的主要组成部分给出一个清晰的概述。
根据攻击者能力
对抗性攻击可以发生在两个阶段,即模型训练和模型测试。这取决于攻击者加入对抗性扰动的能力:
- 对抗攻击:攻击发生在 GNN 模型训练后或测试阶段。模型是固定的,攻击者无法改变模型参数或结构。
- 中毒攻击:攻击发生在 GNN 模型训练之前。攻击者可以在模型训练数据中添加“有毒数据”,让训练好的模型出现故障。
根据扰动类型
攻击者可以从不同方面加入对抗性扰动。扰动可以分为修改节点特征、添加/删除边以及添加假节点。攻击者还应该使扰动不被察觉,否则很容易被检测到。
- 修改节点特征:攻击者可以在保持图结构的同时稍微改变节点特征。
- 添加/删除边:攻击者可以在一定的总扰动预算下为现有节点添加或删除边。
- 添加假节点:攻击者可以将假节点插入到图中,并将其与图中的一些良性节点链接起来。
根据攻击者的目标
根据攻击的目标,我们可以将节点级分类的攻击分为以下两类:
- 目标攻击:有一小组测试节点,攻击者的目的是让经过训练的模型对这些测试样本进行错误分类( V t ⊂ V {V_t} \subset V Vt⊂V)。我们可以进一步将目标攻击分为(1)直接攻击,攻击者直接修改目标节点的特征或边;(2)影响者攻击,攻击者只能操纵其他节点来影响目标。
- 无目标攻击:攻击者的目的是加入有毒数据,让训练好的模型在所有测试数据上整体表现不佳( V t = V {V_t} = V Vt=V)。
然而,对于图级分类,也存在有针对性和无针对性的攻击。有针对性的攻击旨在诱导模型为给定的图样本给出特定的标签,而无针对性的攻击只是希望模型执行错误。
根据攻击者的知识
攻击者的知识是指攻击者对攻击的模型了解多少信息。通常有以下三种设置:
- 白盒攻击:有关模型参数、训练输入(例如邻接矩阵和属性矩阵)和标签的所有信息都提供给攻击者。
- 灰盒攻击:攻击者对受害者模型的了解有限。例如,攻击者无法访问模型参数,但可以访问训练标签。然后它可以利用训练数据来训练代理模型来估计受害者模型的信息。
- 黑盒攻击:攻击者无权访问模型的参数或训练标签。它可以访问邻接矩阵和属性矩阵,并对输出分数或标签进行黑盒查询。
受害者模型
在这一部分中,我们将总结已被证明容易受到对抗性示例影响的受害者模型。
图神经网络:图神经网络是学习图表示的强大工具[56; 73]。最成功的 GNN 变体之一是图卷积网络(GCN)[34]。GCN 通过不断聚合和转换来自其邻居节点的信息来学习每个节点的表示。尽管 GNN 可以在各种任务中实现高性能,但研究表明,包括 GCN 在内的 GNN 很容易受到对抗性攻击[89; 56]。此外,从最近的作品中可以明显看出[89; 87; 44]其他图神经网络包括列网络(CLN)[52]、图注意网络(GAT)[63]和JKNet[77]也有同样的问题。
其他图学习算法:除了图神经网络之外,攻击者还可能攻击其他一些重要的图算法,例如网络嵌入,包括 LINE [59] 和 Deepwalk [51]、基于图的半监督学习(G-SSL)[88] 和知识图谱嵌入[8; 42]。
图对抗攻击
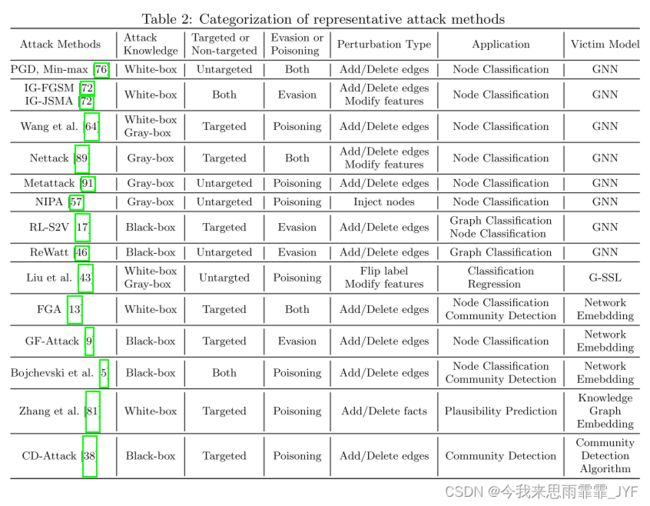
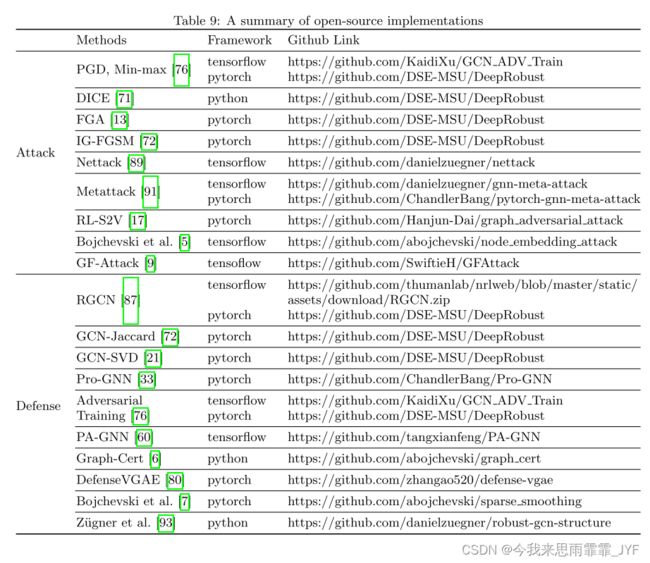
在本节中,我们将回顾图对抗攻击的代表性算法。在上一节的分类之后,我们首先将这些算法划分为白盒、灰盒和黑盒,然后对于每一类中的算法,我们进一步将它们分为有针对性和非针对性攻击。需要注意的是,如无特别提及,以下攻击方式主要针对节点级分类。代表性攻击方法的总体分类如表2所示。此外,表 9 列出了一些代表性算法的开源实现。
白盒攻击
在白盒攻击设置中,攻击者可以访问有关受害者模型的任何信息,例如模型参数、训练数据、标签和预测。尽管在大多数现实情况下我们无法获得此类信息,但我们仍然可以评估受害者模型在最坏情况下的脆弱性。通常,白盒攻击使用受害者模型的梯度信息来指导攻击的生成[13; 76; 72; 10]。
有针对性的攻击
有针对性的攻击旨在误导受害者模型对某些目标样本做出错误的预测。许多研究都遵循白盒定向攻击设置,并在现实世界中广泛应用。FGA[13]从GCN中提取链接梯度信息,然后贪婪地选择绝对梯度最大的节点对来迭代修改图。提出了基于遗传算法的Q-Attack来攻击许多社区检测算法[10]。基于训练好的图自动编码器中的梯度信息的迭代梯度攻击(IGA),被引入到攻击链接预测中[11]。此外,[81]研究了知识图嵌入的漏洞,并且攻击者可以有效地操纵知识图中任意事实的合理性。基于 GNN 的推荐系统也容易受到对抗性攻击,如[86]所示。此外,在攻击节点级分类方面也有很大的努力。传统的图像攻击方法都是利用模型的梯度来寻找对抗实例。但是,由于图数据的离散性,直接计算模型的梯度可能会失败。为了解决这一问题,文献[72]提出利用积分梯度[58]来更好地搜索对抗边和特征扰动。在攻击过程中,攻击者反复选择对对抗目标影响最大的边或特征。通过这种方式,可以使受害者模型以更高的成功率对目标节点进行错误分类。该工作[79]假设图中存在一组“恶意用户”节点。当它们翻转图中任意目标节点的边时,就会导致 GNN 模型对目标节点做出错误的预测。这些“恶意用户”节点对于 GNN 模型的安全至关重要。例如,维基百科的恶作剧文章与真实文章的联系很少且随机。操纵这些恶作剧文章的连接将导致系统对真实文章的类别做出错误的预测。
无目标攻击
目前针对无目标白盒攻击的研究并不多,拓扑攻击[76]是一种代表性算法。它首先构造一个二元对称扰动矩阵 S ∈ { 0 , 1 } n S \in {\{ 0,1\} ^n} S∈{0,1}n,其中 S i j = 1 {S_{ij}} = 1 Sij=1 表示翻转 i i i 和 j j j 之间的边, S i j = 0 {S_{ij}} = 0 Sij=0 表示对 A i j {A_{ij}} Aij 不进行修改。因此,攻击者的目标是在给定一个有限的边扰动预算下找到使预定义攻击损失最小化的 S S S,即 ∥ S ∥ 0 ≤ Δ {\left\| S \right\|_0} \le \Delta ∥S∥0≤Δ。它考虑了两种不同的攻击场景:攻击具有固定参数 θ \theta θ 的预训练GNN,以及攻击可重新训练的GNN f θ {f_\theta } fθ。为了攻击固定的 f θ {f_\theta } fθ,问题可以表述为:
min S ∈ { 0 , 1 } n L a t k ( f θ ( S , A , X ) ) \mathop {\min }\limits_{S \in {{\{ 0,1\} }^n}} {L_{atk}}({f_\theta }(S,A,X)) S∈{0,1}nminLatk(fθ(S,A,X)) 其中 ∥ S ∥ 0 ≤ Δ {\left\| S \right\|_0} \le \Delta ∥S∥0≤Δ
它利用[47]中的投影梯度下降(PGD)算法来搜索最优 S S S。请注意,工作[47]也是图像领域中一种流行的攻击算法。对于可重新训练的 GNN,参数 θ \theta θ 将在对抗性操作后重新训练。因此,攻击问题被表述为最小-最大形式,其中内部最大化是通过最大化攻击损失来更新 θ \theta θ,并且可以通过梯度上升来解决,而外部最小化可以通过PGD来解决。另一项关于无目标白盒攻击的工作旨在通过扰乱网络(图)来攻击多网络挖掘[85]。具体来说,在每次迭代中,它测量网络元素(边和节点属性)对挖掘结果的影响,并攻击具有最高影响值的网络元素。
灰盒攻击
白盒攻击假设攻击者可以通过模型参数计算梯度,这在现实场景中并不总是可行的。灰盒攻击的提出是为了在对受害者模型知识有限的情况下生成攻击[89;91;57]。通常,他们首先用标注的训练数据训练代理模型来逼近受害者模型的信息,然后产生扰动来攻击代理模型。值得注意的是,这些模型需要访问训练数据的标签,因此它们不是将在下一小节中介绍的黑盒攻击。
有针对性的攻击
针对灰盒攻击的早期工作是用于图聚类[15]。结果表明,在域名系统 (DNS) 查询图中注入噪声会降低图嵌入模型的性能。与[15]不同的是,工作[89]提出了一种称为Nettack的攻击方法来生成结构和特征攻击。此外,他们认为,仅仅限制扰动预算并不能总是使扰动“不被注意”。他们建议扰动图还应该保持重要的图属性,包括度分布和特征共现。因此,Nettack 首先选择不违反原始图的度分布和特征共现的可能扰动候选者。然后它贪婪地选择得分最大的扰动来修改图。此外,它表明这种图攻击也可以从一个模型转移到另一个模型,就像图像领域的攻击一样[25]。作者还进行影响者攻击,他们只能操纵除目标之外的节点。事实证明,在给定相同扰动预算的情况下,与直接修改目标节点相比,影响者攻击导致的性能下降幅度较小。
然而,Nettack 由于时间复杂度较高而无法处理大规模图。这项工作 [90] 采用统计分析来研究 Nettack 扰动所表现出的模式。根据对扰动模式的观察,提出了一种可扩展的攻击方法 Fasttack。它首先根据扰动对受害者模型的影响对可能的扰动进行排序,然后选择影响最大的扰动产生攻击。在[67]中,提出了AFGSM算法,它为攻击模型推导出一个时间成本较低的近似封闭解,并将假节点依次注入图中。
另一条工作重点是为图生成后门攻击[83; 74]。后门攻击的目的是找到一些“触发器”(或隐藏模式),当添加到输入时会产生错误分类的结果[66; 14]。为了生成图的后门攻击,攻击者在训练样本中注入触发器(例如精心设计的子图),目的是欺骗 GNN 对带有触发器的样本进行错误分类,同时保持其他测试样本的性能。请注意,图后门攻击可以应用于节点级和图级分类[74]。
无目标攻击
尽管采用与 Nettack 相同的代理模型训练方式,Metatack [91] 是一种无针对性的投毒攻击。它基本上将图结构矩阵视为超参数,攻击者相对于该超参数的损失梯度可由以下方法求得:
∇ G m e t a = ∇ G L a t k ( f θ ∗ ( G ) ) \nabla _G^{meta} = {\nabla _G}{L_{atk}}({f_{{\theta ^*}}}(G)) ∇Gmeta=∇GLatk(fθ∗(G))
注意 ∇ G L a t k ( f θ ∗ ( G ) ) {\nabla _G}{L_{atk}}({f_{{\theta ^*}}}(G)) ∇GLatk(fθ∗(G)) 实际上是一个关于 G G G 和 θ \theta θ 的函数。基于元梯度,采用贪心方法对扰动进行选择。具体来说,给定节点对 ( u , v ) (u,v) (u,v) 的元梯度,它定义了一个得分 S ( u , v ) = ∇ A u v m e t a ( − 2 ⋅ A u v + 1 ) S(u,v) = \nabla _{{A_{uv}}}^{meta}( - 2 \cdot {A_{uv}} + 1) S(u,v)=∇Auvmeta(−2⋅Auv+1),并贪婪地选择得分最高但满足Nettack中不引人注意的约束的扰动。
(NIPA)[57]提出了一种用于节点注入中毒攻击的新型强化学习方法,该方法将假节点注入图数据中,而不是修改现有节点的连通性。具体来说,NIPA 首先将单例 n n n 个节点注入到原始图中。然后在每个动作 a t {a_t} at 中,攻击者首先选择一个注入节点与图中的另一个节点连接,然后给注入节点分配一个标签。通过顺序执行这些操作,最终的图在统计上与原始图相似,但会降低整体模型性能。
黑盒攻击
不同于灰盒攻击,黑盒攻击[17;46;57;5;9;44]更具有挑战性,因为攻击者只能访问邻接矩阵、属性矩阵和受害者模型的输出。禁止访问参数、标签和预测概率。
针对性攻击
如前所述,训练代理模型需要访问训练数据的标签,这并不总是可行的。我们希望找到一种方法,我们只需要对受害者模型[17]进行黑盒查询或以无监督的方式攻击受害者[5;9]。
为了对受害者模型进行黑盒查询,引入了强化学习。RL-S2V[17]是第一个在黑盒设置下使用强化学习技术对图数据产生对抗攻击的作品。他们将攻击过程建模为马尔可夫决策过程(MDP),并允许攻击者修改 m m m 条边来改变目标节点 u u u 的预测标签。他们同时研究节点级(有针对性的)和图级(无针对性的)攻击。对于节点级攻击,它们将MDP定义如下:
状态:状态 s t {s_t} st 由元组 ( G ( t ) , u ) ({G^{(t)}},u) (G(t),u) 表示,其中 G ( t ) {G^{(t)}} G(t) 是时间步 t t t 处的修改图。
操作:时间步 t t t 处的单个操作表示为 a t {a_t} at。对于 a t {a_t} at 的每个操作,攻击者可以选择在图中添加或删除一条边。此外,应用层次结构对动作空间进行分解。
奖励机制:由于攻击者的目标是改变目标节点 u u u 的分类结果,因此RL-S2V在MDP结束时给予攻击者非零奖励 r r r:
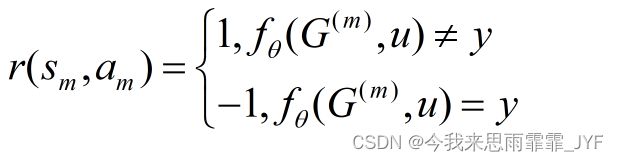
在中间步骤中,攻击者没有获得任何奖励。
终止条件:当攻击者完成修改 m m m 条边时,该过程终止。
由于它们以类似的方式定义了图级攻击的MDP,所以我们省略了细节。并采用Q-learning 算法[50]求解MDP,引导攻击者修改图。
工作[5]展示了一种在黑盒设置中攻击节点嵌入模型系列的方法,而不是攻击节点级分类。受到 DeepWalk 可以用矩阵分解形式表达的启发 [53],他们通过执行 Δ 边翻转,利用矩阵扰动理论最大化无监督 DeepWalk 损失。进一步证明了扰动结构可以转移到其他模型,如 GCN 和标签传播。然而,该方法仅考虑结构信息。GF-Attack [9]被提出将特征信息合并到攻击模型中。具体来说,他们用图滤波器建立了图嵌入方法和一般图信号处理之间的联系,并基于图滤波器和属性矩阵构造了攻击者。GF-Attack 还可以迁移到其他网络嵌入模型,并取得比[5]中的方法更好的性能。
无目标攻击
有人认为,仅限制修改边数量的扰动可能不够隐蔽。提出了一种新颖的框架ReWatt [46]来解决这个问题并执行无目标的图级攻击。ReWatt 采用强化学习框架,采用重新布线操作,而不是在一次修改中简单地添加/删除边,以使扰动更加隐蔽。一次重新连线操作涉及三个节点 v1、v2 和 v3,其中 ReWatt 删除 v1 和 v2 之间的现有边并连接 v1 和 v3。ReWatt 还约束 v3 为 v1 的 二阶邻居,以使扰动更小。这种重接线操作不会改变图中的节点数和边数,并进一步证明了这种重接线操作对代数连通性和有效图阻的影响比添加/删除边的影响要小,而代数连通性和有效图阻是基于图拉普拉斯的重要图性质。
为了以更现实的方式执行图对抗攻击,工作[44]提出了一个更受限制的黑盒设置,攻击者只能访问节点的一个子集,并且只能攻击其中的一小部分。在此设置下,需要攻击者分两步生成攻击:1)在节点访问受限的情况下,选择一个小的节点子集进行攻击;2)在扰动预算下修改节点特征或边。通过利用GNN模型的结构归纳偏差[77;36]作为攻击信息源,对节点级分类任务提出了一种实用的贪婪对抗攻击方法,有效地降低了gnn的性能。
针对图对抗性攻击的对策
在前面的章节中,我们已经证明图神经网络很容易被图数据上不明显的扰动所愚弄。图神经网络的脆弱性给将其应用于安全关键型应用带来了巨大的挑战。为了保护图神经网络免受这些攻击,人们提出了不同的对策。现有的方法可以分为以下类型:(1)对抗性训练,(2)对抗性扰动检测,(3)可证明的鲁棒性,(4)图纯化,(5)注意力机制。
对抗性训练
对抗性训练是图像数据中广泛使用的对抗性攻击的对策[25]。对抗训练的主要思想是将对抗样本注入训练集中,使得训练后的模型能够正确地对该类型的对抗样本进行分类。同样,我们也可以采用这种策略来防御图对抗攻击,如下:
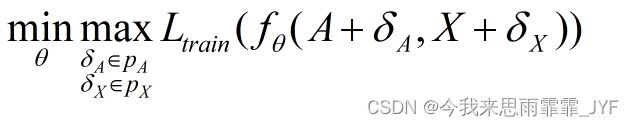
其中 δ A {\delta _A} δA、 δ X {\delta _X} δX 分别表示 A A A、 X X X 上的扰动; p A {p_A} pA 和 p X {p_X} pX 代表不可察觉的扰动域。等式中的最小-最大优化问题表明对抗训练涉及两个过程:(1) 生成使预测损失最大化的扰动,以及 (2) 更新使预测损失最小化的模型参数。通过迭代交替上述两个过程,我们可以训练一个针对对抗性攻击的鲁棒模型。由于有两个输入,即邻接矩阵 A A A 和属性矩阵 X X X,因此可以分别对它们进行对抗训练。为了对邻接矩阵产生扰动,建议在对抗训练期间随机丢弃边[17]。虽然这种简单的策略不能导致分类准确率非常显着的提高(提高 1%),但它通过这种廉价的对抗性训练显示出了一定的有效性。此外,投影梯度下降用于在离散输入结构上生成扰动,而不是随机丢弃边[76]。另一方面,提出了一种具有动态正则化的对抗训练策略来扰乱输入特征[22]。具体来说,它将目标样本的预测与连通样本之间的分歧纳入对抗训练的目标,旨在攻击和重构图的平滑性。此外,提出了批量虚拟对抗训练[19]来提高 GNN 的平滑性,并使 GNN 对对抗性扰动更加鲁棒。在[12; 18; 69; 20]中引入了对输入层的其他几个变体的对抗训练。
上述对抗性训练策略面临两个主要缺点:(1) 它们分别对A和X产生扰动; (2)由于其离散性,图结构不易被扰动。为了克服这些缺点,潜在对抗训练方法不是在输入上生成扰动,而是在第一个隐藏层上注入扰动[32]:
min θ max δ ∈ p L t r a i n ( f θ ( G ; H ( 1 ) + δ ) ) \mathop {\min }\limits_\theta \mathop {\max }\limits_{\delta \in p} {L_{train}}({f_\theta }(G;{H^{(1)}} + \delta )) θminδ∈pmaxLtrain(fθ(G;H(1)+δ))
其中 H ( 1 ) {H^{(1)}} H(1) 表示第一个隐藏层的表示矩阵, δ ∈ p {\delta \in p} δ∈p 是对 H H H 的一些扰动。值得注意的是,隐藏表示是连续的,并且它结合了来自图结构和节点属性的信息。
对抗性扰动检测
为了在测试阶段抵御图对抗性攻击,有一种主要策略称为对手检测。这些检测模型通过探索对抗性边/节点和干净边/节点之间的内在差异来保护 GNN 模型 [78; 28]。这项工作[78]是第一个提出检测方法来寻找图数据上的对抗性示例的工作。它引入了四种方法来区分对抗性边或节点与干净的边或节点,包括(1)链接预测(2)子图链接预测(3)图生成模型和(4)异常值检测。这些方法对正确检测对抗性扰动有一定帮助。工作[28]介绍了一种随机抽取节点子集的方法,并依赖于图感知标准,在使用半监督学习(SSL)模块之前明智地筛选出受污染的节点和边。所提出的模型可用于检测不同的异常生成模型以及对抗性攻击。
可证明的鲁棒性
之前引入的对抗性训练策略是启发式的,仅显示出实验性的好处。然而,即使当前的攻击失败,我们仍然不知道是否存在对抗性例子。因此,就有了作品[92; 6; 30; 7; 93; 61; 65]考虑认真推理图神经网络的安全性,试图证明 GNN 的鲁棒性。众所周知,GNN 对一个节点 v t {v_t} vt 的预测始终取决于其邻居节点。在[92]中,他们提出了这样的问题:图中的哪些节点在其相邻节点属性受到任何可接受的扰动的风险下是安全的。 为了回答这个问题,对于每个节点 v v v 及其相应的标签 y v {y_v} yv,他们尝试精确计算最大化边际损失的上限 U ( v ) U(v) U(v):
U ( v ) ≥ max G ′ ∈ g ( max i ≠ y Z v , i ( G ′ ) − Z v , y ( G ′ ) ) U(v) \ge \mathop {\max }\limits_{G' \in g} (\mathop {\max }\limits_{i \ne y} {Z_{v,i}}(G') - {Z_{v,y}}(G')) U(v)≥G′∈gmax(i=ymaxZv,i(G′)−Zv,y(G′))
其中 g g g 表示所有允许的图扰动的集合(在[92]中仅属性扰动)。这个上限 U U U 称为节点 v v v 的证书。在认证过程中,对于 v v v,如果 U ( v ) ≤ 0 U(v) \le 0 U(v)≤0,任何扰动都不会导致模型对错误类( i ≠ y {i \ne y} i=y)给予比类 y v {y_v} yv 更大的分数,因此 g g g 中不存在对抗性攻击可以改变模型的预测。在测试阶段,他们计算所有测试节点的证书,从而可以知道图中有多少节点在属性扰动下是绝对安全的。而且,这个证书是可训练的,直接最小化证书将有助于更多的节点变得安全。然而,工作[92]只考虑了节点属性的扰动。从不同的角度分析可证明的鲁棒性,在[6]中,它处理的是攻击者仅操纵图结构的情况。它同样计算一个稳健性证书作为个性化 PageRank [29] 的线性函数,这使得优化易于处理。在[93]中,它还试图证明图神经网络在图结构扰动下的鲁棒性。该算法利用联合约束双线性规划方法成功地解决了认证问题。在[65]中,它借鉴了随机平滑[16]的思想来实现结构扰动下图的可证明的鲁棒性。同时,[7]中考虑了认证过程中图数据的稀疏性。该算法提高了认证的效率和准确性,使认证既能抵抗对图特征的攻击,又能抵抗对图结构的攻击。此外,还有研究 GNN 其他应用(例如社区检测)的可证明鲁棒性的工作[30]。
图纯化
对抗性训练或可认证的防御方法都只针对抵抗对抗攻击,这意味着攻击发生在测试期间。而图净化防御方法主要侧重于防御中毒攻击。由于中毒攻击会将毒物加入到训练图中,因此净化方法的目的是净化中毒图,并在此基础上学习鲁棒图神经网络模型。实现图净化的方法有两种:预处理[72;21]和图学习[33;35]。
预处理
预处理方法首先对扰动图数据进行提纯,然后在提纯后的图上训练GNN模型。这样,GNN 模型就可以在干净的图上进行训练。文献[72]基于对攻击方法的两种经验观察,提出了一种净化方法:(1)攻击者倾向于增加边,而不是删除边或修改特征。(2)攻击者倾向于连接不同的节点。因此,他们提出了一种防御方法,通过消除两个端节点具有小Jaccard相似性[54]的边。由于这两个节点是不同的,它们在现实中可能没有连接,它们之间的边可能是对抗性的。实验结果证明了所提出的防御方法的有效性和效率。然而,这种方法只有在节点特征可用的情况下才有效。在[21]中,可以观察到Nettack[89]产生的扰动主要是改变图邻接矩阵的小奇异值。因此,它建议通过使用截断的 SVD 来纯化扰动的邻接矩阵,以获得其低秩近似。它进一步表明,仅保留邻接矩阵的前 10 个奇异值就能够防御 Nettack 并提高 GNN 的性能。
图学习
预处理可能不是净化图的理想选择,因为它独立于 GNN 的训练过程,并且可能会错误地删除正常边。另一种净化策略是图学习,其目标是消除对抗模式并获得干净的图结构。传统的图学习方法[23; 31]不会直接处理对抗性攻击。因此,为了使 GNN 更加鲁棒,利用对抗性攻击的特征来指导图学习过程非常重要。在[33]中,它证明了对抗性攻击本质上会违反一些重要的图属性,即低秩、稀疏性和特征平滑性。然后,它探索这些图属性来设计鲁棒的图神经网络 Pro-GNN,它共同学习干净的图结构和鲁棒的 GNN 参数。具体来说,Pro-GNN 通过保留上述属性来更新图结构,并在更新的图结构上训练 GNN 参数。在[80]中,采用变分图自动编码器[35]来重建图结构,这也可以减少对抗性扰动的影响。
注意力机制
与试图排除对抗性扰动的净化方法不同,基于注意力的防御方法旨在通过惩罚模型在对抗性边或节点上的权重来训练鲁棒的 GNN 模型 [87; 60; 82]。基本上,这些方法学习一种注意力机制来区分对抗性边和节点与干净的边和节点,然后减少对抗性扰动对 GNN 聚合训练过程的贡献。这项工作[87]假设对抗性节点可能具有很高的预测不确定性,因为对手倾向于将该节点与来自其他社区的节点连接起来。为了惩罚这些不确定节点的影响,他们提出了一种名为 RGCN 的防御方法,将节点的第 l l l 层隐藏表示 h i ( l ) h_i^{(l)} hi(l) 建模为均值为 μ i ( l ) \mu _i^{(l)} μi(l) 和方差为 σ i ( l ) \sigma _i^{(l)} σi(l) 的高斯分布:
h i ( l ) ∼ N ( μ i ( l ) , d i a g ( σ i ( l ) ) ) h_i^{(l)} \sim N(\mu _i^{(l)},diag(\sigma _i^{(l)})) hi(l)∼N(μi(l),diag(σi(l)))
其中不确定性可以反映在方差 σ i ( l ) \sigma _i^{(l)} σi(l) 中。当聚合来自邻居节点的信息时,它应用注意机制来惩罚具有高方差的节点:
α i ( l ) = exp ( − γ σ i ( l ) ) \alpha _i^{(l)} = \exp ( - \gamma \sigma _i^{(l)}) αi(l)=exp(−γσi(l))
其中, α i ( l ) \alpha _i^{(l)} αi(l) 是分配给节点 i i i 的注意力分数, γ \gamma γ 是超参数。此外,经验证,受攻击的节点确实比正常节点具有更高的方差,并且所提出的注意机制确实有助于减轻对抗性攻击带来的影响。从不同的角度来看,GNNGuard被提出利用网络同质性理论[49]为连接相似节点的边分配更高的分数,同时修剪不相关节点之间的边[82]。
在[60]中,提出为了提高一个目标GNN模型的鲁棒性,可以将其他与目标图具有相似拓扑分布和节点属性的干净图的信息纳入其中。例如,Facebook和Twitter拥有共享类似域的社交网络图表数据;Yelp和Foursquare也有类似的共同评论图表数据。
图攻击和防御的存储库
在本节中,我们将简要介绍我们为对抗攻击和防御开发的存储库DeepRobust2[41]。为了便于对抗性攻击和防御的研究,DeepRobust 包含了大多数针对图数据和图像数据的代表性攻击和防御算法。该存储库可以使研究人员通过实证研究加深对攻击和防御的理解。具体来说,对于图对抗学习,DeepRobust 提供了 7 个数据集:四个引文图,包括 Cora [55]、Cora-ML [4]、Citeseer [4] 和 Pubmed [55]、一个共同作者图 ACM [68]、一个博客图 Polblogs [1] 和一个社交图 BlogCatalog [27]。除此之外,DeepRobust涵盖了以下攻击和防御:(1)5种有针对性的攻击算法,即FGA[13]、Nettack[89]、RL-S2V[17]、集成梯度攻击[72]和随机攻击[ 89];(2) 3种非针对性算法,即Metatack[91]、Topology攻击[76]和DICE[70];(3)一种受害者模型,即GCN[34]; (4) 5种防御算法,即对抗训练[25]、GCN-Jaccard [72]、GCN-SVD [21]、RGCN [87]和Pro-GNN [33]。
DeepRobust 是一个易于使用的平台,适合从事对抗性攻击和防御的研究人员。借助 Deep Robust,用户可以通过攻击 API 训练攻击模型或加载存储库提供的预攻击图来生成图对抗攻击。可以使用防御 API 在扰动图上训练鲁棒模型。一旦我们获得了扰动图和训练好的防御模型,就可以将它们输入到评估API中进行相互竞争,并报告相应攻击下的模型性能。在下一节中,我们使用 DeepRobust 对图对抗攻击进行实证研究。
https://github.com/DSE-MSU/DeepRobust
实证研究
在 DeepRobust 的帮助下,我们能够对图对抗攻击进行实证研究并发现其重要模式。接下来我们首先介绍实验设置,然后介绍实证结果和发现。
实验设置
在不同的设置下设计了不同的攻击和防御方法。我们使用最流行的设置之一——无目标中毒设置进行实验。相应地,我们选择针对此设置设计的代表性攻击和防御方法。采用三种代表性的攻击方法来产生扰动,包括DICE[70]、Metatack[91]和拓扑攻击[76]。值得注意的是,DICE 是一种白盒攻击,它随机连接具有不同标签的节点或丢弃共享相同标签的节点之间的边。为了评估不同防御方法在对抗性攻击下的性能,我们比较了自然训练的 GCN [34] 和四种防御方法在这些攻击图上的鲁棒性,即 GCN [34]、GCN-Jaccard [72]、GCN-SVD [21]、RGCN [87] 和 GAT [62]。遵循[91],我们使用三个数据集:Cora、Citeseer 和 Polblogs。对于每个数据集,我们随机选择 10% 的节点进行训练,10% 的节点进行验证,其余 80% 的节点进行测试。我们将每个实验重复 5 次并报告平均性能。在Cora和Citeseer数据集上,采用最具破坏性的变体CE-min-max[76]来实施拓扑攻击。但是CE-min-max无法在Polblogs数据集上收敛,我们在此数据集上采用了另一种变体,称为CE-PGD [76]。
被攻击图分析
了解攻击方法行为的一种方法是比较干净图和受攻击图的属性。在本小节中,我们将从全局和局部两个角度进行分析。
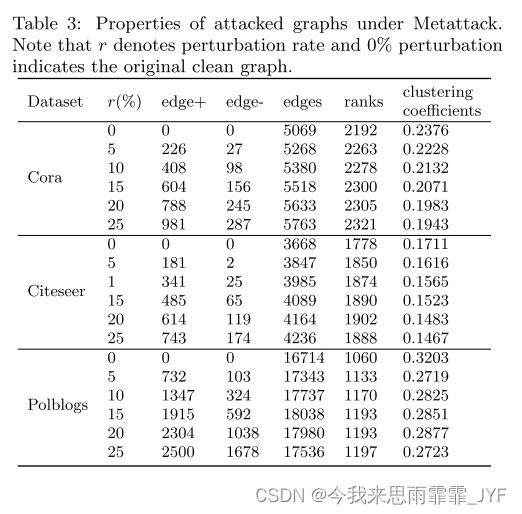
全局: 我们从对三个数据集的三种攻击生成的干净图和扰动图中收集了五个全局属性。这些属性包括添加边的数量、删除边的数量、边的数量、相邻矩阵的秩和聚类系数。我们仅在表3中显示Metatack的结果。拓扑攻击和 DICE 的结果可在附录 A.1 中找到。请注意,我们将扰动率从 0% 更改为 25%,步长为 5%,0% 扰动表示原始的干净图。从表中可以看出:
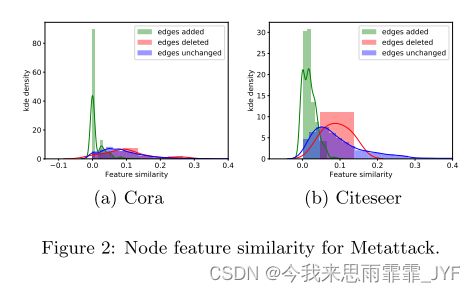
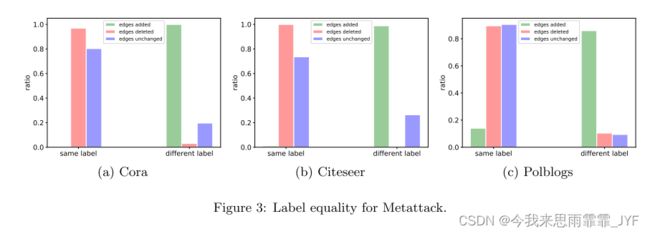
局部: 我们还研究了两个局部属性,包括由三种边连接的两个节点之间的特征相似性和标签相等性:新增边、删除边以及未被攻击方法改变的正常边。由于特征在我们的数据集中是二进制的,我们使用jaccard相似性作为特征相似性的度量。对于标签相等,我们报告两个节点共享相同标签或具有不同标签的比率。特征相似度和标签相等结果分别如图 2 和图 3 所示。我们展示了具有 5% 扰动的 Metatack 的结果。拓扑攻击和 DICE 的结果可在附录 A.2 中找到。请注意,我们在 Polblogs 上没有特征相似度结果,因为该数据集没有节点特征。我们可以从图中得出以下观察结果:
- 攻击者倾向于连接具有不同特征和不同标签的节点。如图2和图3所示,大多数添加的边连接的是具有非常不同的特征和不同标签的节点。
- 攻击者倾向于从具有相似特征和相同标签的节点上删除边。如图2和图3所示,大部分被删除的边原本连接的是具有相似特征和相同标签的节点。
攻防性能
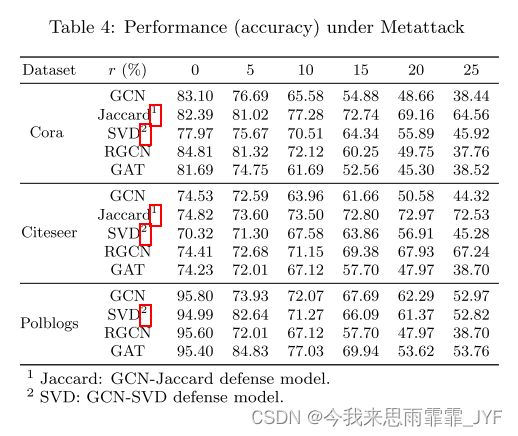
在本小节中,我们将研究攻击方法的执行方式以及防御方法是否有助于抵御攻击。类似地,我们以5%的步长将扰动率从0变化到25%。结果如表4所示。我们展示Metattack的性能。拓扑攻击和DICE的结果见附录A.3。注意,我们在polblog中没有Jaccard防御模型的性能,因为这种模式需要节点特性,而polblog不提供节点特性。根据结果,我们有以下观察:
- 随着扰动的增加,GCN的性能急剧下降。这一结果表明Metattack可以导致GCN模型的精度显著降低。
- 当扰动很小时,我们观察到防御方法的性能略有下降,这表明它们的有效性。然而,当图严重中毒时,其性能也会显着下降,这表明需要努力防御严重中毒攻击。
结论和未来研究方向
在本次调查中,我们全面概述了一个新兴的研究领域——图数据的对抗性攻击和防御。我们研究了图对抗性攻击的分类,并回顾了代表性的对抗性攻击和相应的防御措施。此外,我们还进行了实证研究,以展示不同防御方法在不同攻击下的表现,以及重要的图属性在攻击下的变化。通过这次全面的研究,我们对这一领域有了更深入的了解,从而可以探讨一些有前途的研究方向。
- 难以察觉的扰动措施:与图像数据不同,人类无法轻易判断图上的扰动是否不可察觉。对扰动的 l 0 {l_0} l0 范数约束肯定是不够的。目前只有很少的现有工作研究这个问题,因此寻找简洁的扰动评估方法刻不容缓。
- 不同的图形数据:现有的工作主要集中在具有节点属性的静态图。诸如具有边属性的图和动态图之类的复杂图尚未得到充分研究。
- 图对抗性例子的存在性和可转移性:目前讨论图对抗样本的存在性和可迁移性的著作很少。研究这个主题对于我们理解图学习算法非常重要,从而帮助我们构建强大的模型。
- 可扩展性:攻击方法的高度复杂性阻碍了它们在实际应用中的使用。然而,在时间复杂度方面开发高效攻击方法的工作却很少。此外,鉴于大多数攻击算法都是基于梯度的,如何降低其内存复杂度也仍然是一个挑战。