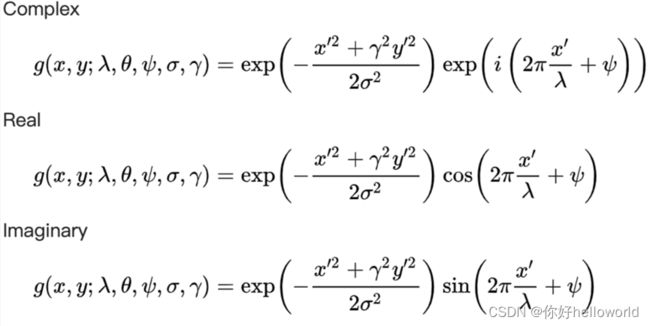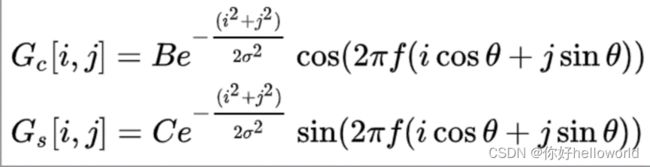基于纹理特征的kmeas聚类的图像分割方案
Gabor滤波器简介
在图像处理中,以Dennis Gabor命名的Gabor滤波器是一种用于纹理分析的线性滤波器,本质上是指在分析点或分析区域周围的局部区域内,分析图像中是否存在特定方向的特定频率内容。Gabor滤波器的频率和方向表示被许多当代视觉科学家认为与人类视觉系统的频率和方向表示相似。它们被发现特别适合于纹理表征和辨别。
在空间域,二维Gabor滤波器是由正弦平面波调制的高斯核函数(见Gabor变换)。
定义
由于Gabor滤波器脉冲响应的乘法卷积性质(卷积定理),其傅里叶变换等于谐波函数(正弦函数)的傅里叶变换与高斯函数的傅里叶变换的卷积。滤波器有一个实分量和一个虚分量表示正交方向。这两个分量可以组成一个复数,也可以单独使用。
图像特征提取
一组不同频率和方向的Gabor滤波器可能有助于从图像中提取有用的特征。在离散域中,二维Gabor滤波器:
其中B和C是待确定的归一化因子。
二维Gabor滤波器在图像处理中有着丰富的应用,特别是在纹理分析和分割的特征提取方面。f定义了在纹理中寻找的频率。通过改变theta,我们可以寻找面向特定方向的纹理。通过改变sigma,我们改变了支持或被分析图像区域的大小。
2-D Gabor滤波器在图像处理的应用
在图像处理中,Gabor特征是识别的理想选择。在文档图像处理中,Gabor特征是识别多语言文档中单词的脚本的理想选择由于文本具有丰富的高频成分,而图片本质上相对平滑,不同频率和不同方向的Gabor滤波器已被用于从复杂文档图像(包括灰色和彩色)中定位和提取纯文本区域。它还被应用于面部表情识别。Gabor滤波器在模式分析中也得到了广泛的应用。例如,它已被用于研究脊柱多孔海绵状小梁内的指向性分布。Gabor空间在光学字符识别、虹膜识别和指纹识别等图像处理应用中非常有用。特定空间位置的激活之间的关系在图像中的物体之间非常不同。此外,重要的激活可以从Gabor空间中提取,以创建一个稀疏的对象表示。
Gabor在python中的实现
1. #构建Gabor滤波器
2. def build_filters(num_orientations=8):
3. filters = []
4. # 定义多个不同方向的Gabor滤波器参数
5. ksize = [7, 9, 11, 13, 15, 17] # 滤波器的大小
6. sigma = 4.0 # 高斯函数的标准差
7. lambd = 10.0 # 波长
8. gamma = 0.5 # 高斯核的椭圆度
9. # num_orientations = 8 # 设定多个不同方向的Gabor滤波器
10.
11. for theta in np.linspace(0, np.pi, num_orientations, endpoint=False):
12. for k in ksize:
13. gabor_filter = cv2.getGaborKernel((k, k), sigma, theta, lambd, gamma, ktype=cv2.CV_32F)
14. filters.append(gabor_filter)
15.
16. #绘制滤波器
17. plt.figure(1)
18. for temp in range(len(filters)):
19. plt.subplot(8, 6, temp + 1)
20. plt.imshow(filters[temp])
21. plt.show()
22.
23. return filters
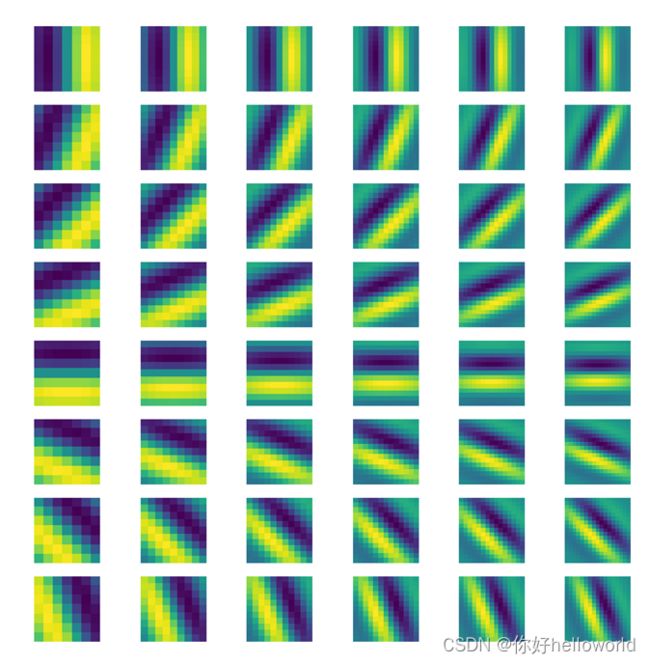
上述代码构建了6个不同尺度下,8个不同方向上,共48个滤波核构成的的Gabor滤波器组,如下图所示
分别使用这48个滤波器组对图像(灰度)进行特征提取,并拼接成特征矩阵,代码如下:
1. #Gabor特征提取
2. def getGabor(img, filters):
3. features_list = [] #滤波结果
4. for filter in filters:
5. # 对图像应用多个不同尺度不同方向的Gabor滤波器,并将特征合并为一个特征向量
6. filtered_image = cv2.filter2D(img, cv2.CV_8UC1, filter)
7. features = filtered_image.reshape(-1)
8. features_list.append(features)
9.
10. feature_matrix = np.array(features_list).T
11. return feature_matrix
该特征矩阵的维度为(H×W,48),即每个像素都有一个48维的特征向量,通过使用kmeans聚类算法计算这些特征向量的相似度,对每个像素进行4分类
1. def kmeansSeg(feature_matrix, num_clusters):
2. # 使用Kmeans进行聚类
3. kmeans = KMeans(n_clusters=num_clusters, random_state=0)
4. kmeans.fit(feature_matrix)
5. # 获取聚类结果
6. labels = kmeans.labels_
7. return labels
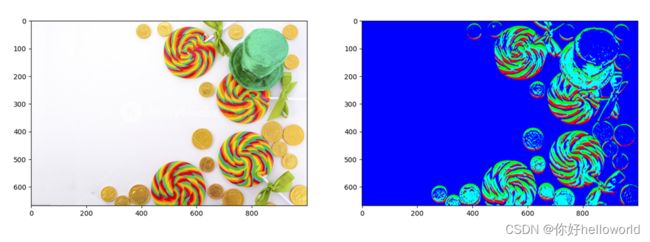
对得到的标签进行颜色映射,输出结果如下
可以看到,当聚类簇数为4时的分割效果是较好的,注意我们在gabor滤波器中只调整了不同的方向和尺度特征,因此得到的聚类效果也是对不同方向下的聚类效果
接下来我们来看在不同聚类簇数下的聚类效果
可以看到,在不同聚类簇数下对纹理特征的聚类效果各不相同,其中当聚类簇数为4时效果较好
完整源码
import cv2
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
class GaborSegmention():
def __init__(self,img,num_orientations = 8):#初始化滤波器
self.img=img
self.filters = []
# 定义6个不同尺度和num_orientations个不同方向的Gabor滤波器参数
ksize = [7, 9, 11, 13, 15, 17] # 滤波器的大小
sigma = 4.0 # 高斯函数的标准差
lambd = 10.0 # 波长
gamma = 0.5 # 高斯核的椭圆度
# num_orientations = 8 # 设定多个不同方向的Gabor滤波器
for theta in np.linspace(0, np.pi, num_orientations, endpoint=False):
for k in ksize:
gabor_filter = cv2.getGaborKernel((k, k), sigma, theta, lambd, gamma, ktype=cv2.CV_32F)
self.filters.append(gabor_filter)
# 绘制滤波器
plt.figure(figsize=(12, 12))
for i in range(len(self.filters)):
plt.subplot(8, 6, i + 1)
plt.imshow(self.filters[i])
plt.axis('off')
plt.show()
def getGabor(self):
feature_matrix=[]
for filter in self.filters:
# 对图像应用6个不同尺度8个不同方向的Gabor滤波器,得到一个h*w特征图
filtered_image = cv2.filter2D(self.img, cv2.CV_8UC1, filter)
# 一个特征图就表示某一个尺度下的某一个方向下的特征
features = filtered_image.reshape(-1)
feature_matrix.append(features)
# 该结果表示每个像素的6个尺度8个方向Gabor特征向量
feature_matrix = np.array(feature_matrix).T
return feature_matrix
def kmeansSeg(self,num_clusters,feature_matrix):
# 使用Kmeans进行聚类,即计算每个像素的特征向量(48个特征)的相似度
kmeans = KMeans(n_clusters=num_clusters, random_state=0)
kmeans.fit(feature_matrix)
# 获取聚类结果
labels = kmeans.labels_
return labels
def colorMap(self, labels):
# 进行像素映射
color_map = np.array([[255, 0, 0], # 蓝色
[0, 0, 255], # 红色
[0, 255, 0], # 绿色
[255, 255, 0],
[0, 255, 255],
[128, 128, 128]
])
# 将聚类结果转化为图像
segmented_image = color_map[labels].reshape(self.img.shape[0], self.img.shape[1], 3).astype(np.uint8)
return segmented_image
if __name__=="__main__":
# 加载图像
# image_path = r"./data/planets.jpg"
image_path = r"./data/coins.jpg"
img = cv2.imread(image_path)
image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# print(image.shape)
# 创建gaborSeg分割对象,初始化gabor滤波器
gaborSeg=GaborSegmention(image)
# 获取特征矩阵
feature_matrix = gaborSeg.getGabor()
# # 分割结果
# labels=gaborSeg.kmeansSeg(num_clusters=4,feature_matrix=feature_matrix)
# segmented_image=gaborSeg.colorMap(labels)
num_clusters=[2,4,6]
seglabels=[ gaborSeg.kmeansSeg(num_clusters=num_cluster,feature_matrix=feature_matrix)
for num_cluster in num_clusters]
segmented_images=[gaborSeg.colorMap(labels) for labels in seglabels]
# 显示结果
plt.figure(figsize=(16, 8))
# 原图
plt.subplot(221)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.axis('off')
# 分割图
for i,segmented_image in enumerate(segmented_images):
plt.subplot(2,2,i+2)
plt.imshow(segmented_image)
plt.title("num_clusters={}".format(num_clusters[i]))
plt.axis('off')
# plt.subplots_adjust(hspace=0.2)
plt.show()