DIff算法优化策略

• ***当前阶段的笔记 ***

「面向实习生阶段」https://www.aliyundrive.com/s/VTME123M4T9 提取码: 8s6v
点击链接保存，或者复制本段内容，打开「阿里云盘」APP ，无需下载极速在线查看，视频原画倍速播放。

优化策略

diff痛点

vue2.x中的虚拟dom是进行全量的对比，在运行时会对所有节点生成一个虚拟节点树，当页面数据发生变更好，会遍历判断virtual dom所有节点（包括一些不会变化的节点）有没有发生变化；虽然说diff算法确实减少了多DOM节点的直接操作，但是这个减少是有成本的，如果是复杂的大型项目，必然存在很复杂的父子关系的VNode,而Vue2.x的diff算法，会不断地递归调用 patchVNode，不断堆叠而成的几毫秒，最终就会造成 VNode 更新缓慢。

Vue2在DOM-Diff过程中，优先处理特殊场景的情况，即头头比对，尾尾比对，头尾比对，尾头比对等。

而Vue3在DOM-Diff过程中，根据 newIndexToOldIndexMap 新老节点索引列表找到最长稳定序列，通过最长增长子序列的算法比对，找出新旧节点中不需要移动的节点，原地复用，仅对需要移动或已经patch的节点进行操作，最大限度地提升替换效率，相比于Vue2版本是质的提升！

那么Vue3.0是如何解决这些问题的呢

动静结合 PatchFlag

来个：

<div>
  <div>{msg}</div>
  <div>静态文字</div>
</div>

在Vue3.0中，在这个模版编译时，编译器会在动态标签末尾加上 /* Text*/ PatchFlag。也就是在生成VNode的时候，同时打上标记，在这个基础上再进行核心的diff算法并且 PatchFlag 会标识动态的属性类型有哪些，比如这里 的TEXT 表示只有节点中的文字是动态的。而patchFlag的类型也很多。这里直接引用一张图片。

其中大致可以分为两类：

• 当 patchFlag 的值「大于」 0 时，代表所对应的元素在 patchVNode 时或 render 时是可以被优化生成或更新的。
• 当 patchFlag 的值「小于」 0 时，代表所对应的元素在 patchVNode 时，是需要被 full diff，即进行递归遍历 VNode tree 的比较更新过程。

看源码：

export function render(_ctx, _cache, $props, $setup, $data, $options) {
 return (_openBlock(), _createBlock("div", null, [
  _createVNode("p", null, "'HelloWorld'"),
  _createVNode("p", null, _toDisplayString(_ctx.msg), 1 /* TEXT */)
 ]))
}
****
复制代码

这里的_createVNode("p", null, _toDisplayString(_ctx.msg), 1 /* TEXT */)就是对变量节点进行标记。

总结：Vue3.0对于不参与更新的元素，做静态标记并提示，只会被创建一次，在渲染时直接复用。

其中还有cacheHandlers（事件侦听器缓存）。

diff算法源码解析

以数组为栗子：

newNode:[a,b,c,d,e,f,g] 
oldNode:[a,b,c,h,i,j,f,g]

步骤1:从首部比较new vnode 和old vnode,如果碰到不同的节点，跳出循环，否则继续，直到一方遍历完成；

由此我们得到newNode和oldNode首部相同的片段为 a,b,c， 

源码：

const patchKeyedChildren = (
    c1,
    c2,
    container,
    parentAnchor,
    parentComponent,
    parentSuspense,
    isSVG,
    optimized
) => {
    let i = 0;  
    const l2 = c2.length
    let e1 = c1.length - 1
    let e2 = c2.length - 1

    while (i <= e1 && i <= e2) {
      const n1 = c1[i]
      const n2 = c2[i]
      if (isSameVNodeType(n1, n2)) {
        patch(
          n1,
          n2,
          container,
          parentAnchor,
          parentComponent,
          parentSuspense,
          isSVG,
          optimized
        )
      } else {
        break
      }
      i++
    }
    
    //这里的isSameVNodeType
      export function isSameVNodeType(n1: VNode, n2: VNode): boolean {
      // 比较类型和key是否一致（）
      return n1.type === n2.type && n1.key === n2.key
      }

Tip:这里的isSameVNodeType从type和key，因此key作为唯一值是非常重要的，这也就解释了 v-for循环遍历不能用index作为key的原因。

步骤2:从尾部比较new vnode 和old vnode,如果碰到不同的节点，跳出循环，否则继续，直到一方遍历完成；

由此我们得到newNode和oldNode尾部相同的片段为 f,g 
while (i <= e1 && i <= e2) {
      const n1 = c1[e1]
      const n2 = c2[e2]
      if (isSameVNodeType(n1, n2)) {
        patch(
          n1,
          n2,
          container,
          parentAnchor,
          parentComponent,
          parentSuspense,
          isSVG,
          optimized
        )
      } else {
        break
      }
      e1--
      e2--
    }
}

在遍历过程中满足i > e1 && i < e2，说明 仅有节点新增

if (i > e1) {
    if (i <= e2) {
        const nextPos = e2 + 1;
        const anchor = nextPos < l2 ? c2[nextPos] : parentAnchor
        while (i <= e2) {
            patch(
                null,
                c2[i],
                container,
                anchor,
                parentComponent,
                parentSuspense,
                isSVG
            )
            i++
        }
    }
} else if {
    ...
} else {
   ...
}

在遍历过程中满足i > e1 && i > e2，说明 仅有节点移除

if (i > e1) {
  //
} else if (i > e2) {
    while (i <= e1) {
        unmount(c1[i], parentComponent, parentSuspense, true)
        i++
    }
} else {
    //
}

步骤3: 节点移动、新增或删除

经过以上步骤，剩下的就是不确定的元素，那么diff算法将遍历 所有的new node，将key和索引存在keyToNewIndexMap中，为map解构，

if (i > e1) {
  //
} else if (i > e2) {
  //
} else {
    const s1 = i
    const s2 = i

    const keyToNewIndexMap = new Map()
    for (i = s2; i <= e2; i++) {
        const nextChild = c2[i]
        if (nextChild.key !== null) {
            keyToNewIndexMap.set(nextChild.key, i)
        }
    }
}

接下来

 for (i = s1; i <= e1; i++) { /* 开始遍历老节点 */
        const prevChild = c1[i]
        if (patched >= toBePatched) { /* 已经patch数量大于等于， */
          /* ① 如果 toBePatched新的节点数量为0 ，那么统一卸载老的节点 */
          unmount(prevChild, parentComponent, parentSuspense, true)
          continue
        }
        let newIndex
         /* ② 如果,老节点的key存在 ，通过key找到对应的index */
        if (prevChild.key != null) {
          newIndex = keyToNewIndexMap.get(prevChild.key)
        } else { /*  ③ 如果,老节点的key不存在 */
          for (j = s2; j <= e2; j++) { /* 遍历剩下的所有新节点 */
            if (
              newIndexToOldIndexMap[j - s2] === 0 && /* newIndexToOldIndexMap[j - s2] === 0 新节点没有被patch */
              isSameVNodeType(prevChild, c2[j] as VNode)
            ) { /* 如果找到与当前老节点对应的新节点那么 ，将新节点的索引，赋值给newIndex  */
              newIndex = j
              break
            }
          }
        }
        if (newIndex === undefined) { /* ①没有找到与老节点对应的新节点，删除当前节点，卸载所有的节点 */
          unmount(prevChild, parentComponent, parentSuspense, true)
        } else {
          /* ②把老节点的索引，记录在存放新节点的数组中， */
          newIndexToOldIndexMap[newIndex - s2] = i + 1
          if (newIndex >= maxNewIndexSoFar) {
            maxNewIndexSoFar = newIndex
          } else {
            /* 证明有节点已经移动了   */
            moved = true
          }
          /* 找到新的节点进行patch节点 */
          patch(
            prevChild,
            c2[newIndex] as VNode,
            container,
            null,
            parentComponent,
            parentSuspense,
            isSVG,
            optimized
          )
          patched++
        }
 }

之后通过 计算出最长递增子序列 减少Dom元素的移动，达到最少的 dom 操作。

Vue3 Diff —— 最长递增子序列

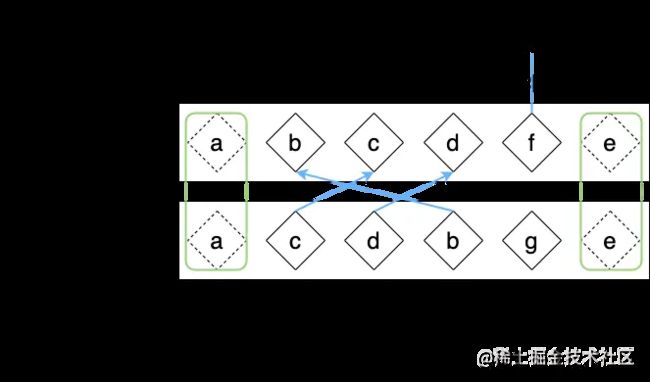
vue3的diff借鉴于inferno，该算法其中有两个理念。第一个是相同的前置与后置元素的预处理；第二个则是最长递增子序列，此思想与React的diff类似又不尽相同。下面我们来一一介绍。

1. 前置与后置的预处理

我们看这两段文字

Hello World
Hey World

其实就简单的看一眼我们就能发现，这两段文字是有一部分是相同的，这些文字是不需要修改也不需要移动的，真正需要进行修改中间的几个字母，所以diff就变成以下部分

text1: 'llo'
text2: 'y'

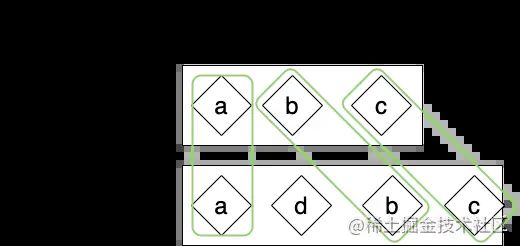
接下来换成vnode，我们以下图为例。

图中的被绿色框起来的节点，他们是不需要移动的，只需要进行打补丁patch就可以了。我们把该逻辑写成代码。

function vue3Diff(prevChildren, nextChildren, parent) {
  let j = 0,
    prevEnd = prevChildren.length - 1,
    nextEnd = nextChildren.length - 1,
    prevNode = prevChildren[j],
    nextNode = nextChildren[j];
  while (prevNode.key === nextNode.key) {
    patch(prevNode, nextNode, parent)
    j++
    prevNode = prevChildren[j]
    nextNode = nextChildren[j]
  }
  
  prevNode = prevChildren[prevEnd]
  nextNode = prevChildren[nextEnd]
  
  while (prevNode.key === nextNode.key) {
    patch(prevNode, nextNode, parent)
    prevEnd--
    nextEnd--
    prevNode = prevChildren[prevEnd]
    nextNode = prevChildren[nextEnd]
  }
}

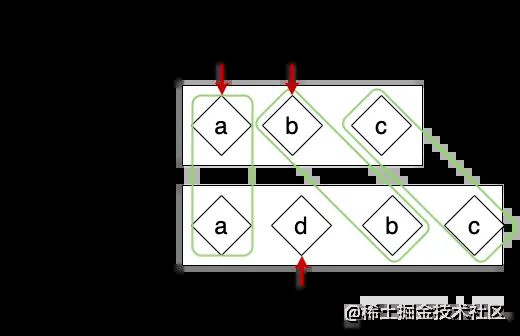
这时候，我们就需要考虑边界情况了，这里有两种情况。一种是j > prevEnd；另一种是j > nextEnd。

我们以这张图为例，此时j > prevEnd且j <= nextEnd，我们只需要把新列表中j到nextEnd之间剩下的节点插入进去就可以了。相反， 如果j > nextEnd时，我们把旧列表中j到prevEnd之间的节点删除就可以了。

function vue3Diff(prevChildren, nextChildren, parent) {
  // ...
  if (j > prevEnd && j <= nextEnd) {
    let nextpos = nextEnd + 1,
      refNode = nextpos >= nextChildren.length
                ? null
                : nextChildren[nextpos].el;
    while(j <= nextEnd) mount(nextChildren[j++], parent, refNode)
    
  } else if (j > nextEnd && j <= prevEnd) {
    while(j <= prevEnd) parent.removeChild(prevChildren[j++].el)
  }
}

我们再继续思考，在我们while循环时，指针是从两端向内逐渐靠拢的，所以我们应该在循环中就应该去判断边界情况，我们使用label语法，当我们触发边界情况时，退出全部的循环，直接进入判断。代码如下：

function vue3Diff(prevChildren, nextChildren, parent) {
  let j = 0,
    prevEnd = prevChildren.length - 1,
    nextEnd = nextChildren.length - 1,
    prevNode = prevChildren[j],
    nextNode = nextChildren[j];
  // label语法
  outer: {
    while (prevNode.key === nextNode.key) {
      patch(prevNode, nextNode, parent)
      j++
      // 循环中如果触发边界情况，直接break，执行outer之后的判断
      if (j > prevEnd || j > nextEnd) break outer
      prevNode = prevChildren[j]
      nextNode = nextChildren[j]
    }

    prevNode = prevChildren[prevEnd]
    nextNode = prevChildren[nextEnd]

    while (prevNode.key === nextNode.key) {
      patch(prevNode, nextNode, parent)
      prevEnd--
      nextEnd--
      // 循环中如果触发边界情况，直接break，执行outer之后的判断
      if (j > prevEnd || j > nextEnd) break outer
      prevNode = prevChildren[prevEnd]
      nextNode = prevChildren[nextEnd]
    }
  }
  
  // 边界情况的判断
  if (j > prevEnd && j <= nextEnd) {
    let nextpos = nextEnd + 1,
      refNode = nextpos >= nextChildren.length
                ? null
                : nextChildren[nextpos].el;
    while(j <= nextEnd) mount(nextChildren[j++], parent, refNode)
    
  } else if (j > nextEnd && j <= prevEnd) {
    while(j <= prevEnd) parent.removeChild(prevChildren[j++].el)
  }
}

2. 判断是否需要移动

其实几个算法看下来，套路已经很明显了，就是找到移动的节点，然后给他移动到正确的位置。把该加的新节点添加好，把该删的旧节点删了，整个算法就结束了。这个算法也不例外，我们接下来看一下它是如何做的。

当前/后置的预处理结束后，我们进入真正的diff环节。首先，我们先根据新列表剩余的节点数量，创建一个source数组，并将数组填满-1。

我们先写这块逻辑。

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  outer: {
  // ...
  }
  
  // 边界情况的判断
  if (j > prevEnd && j <= nextEnd) {
    // ...
  } else if (j > nextEnd && j <= prevEnd) {
    // ...
  } else {
    let prevStart = j,
      nextStart = j,
      nextLeft = nextEnd - nextStart + 1,     // 新列表中剩余的节点长度
      source = new Array(nextLeft).fill(-1);  // 创建数组，填满-1
     
  }
}
复制代码

那么这个source数组，是要做什么的呢？他就是来做新旧节点的对应关系的，我们将新节点在旧列表的位置存储在该数组中，我们在根据source计算出它的最长递增子序列用于移动DOM节点。为此，我们先建立一个对象存储当前新列表中的节点与index的关系，再去旧列表中去找位置。

在找节点时要注意，如果旧节点在新列表中没有的话，直接删除就好。除此之外，我们还需要一个数量表示记录我们已经patch过的节点，如果数量已经与新列表剩余的节点数量一样，那么剩下的旧节点我们就直接删除了就可以了

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  outer: {
  // ...
  }
  
  // 边界情况的判断
  if (j > prevEnd && j <= nextEnd) {
    // ...
  } else if (j > nextEnd && j <= prevEnd) {
    // ...
  } else {
    let prevStart = j,
      nextStart = j,
      nextLeft = nextEnd - nextStart + 1,     // 新列表中剩余的节点长度
      source = new Array(nextLeft).fill(-1),  // 创建数组，填满-1
      nextIndexMap = {},                      // 新列表节点与index的映射
      patched = 0;                            // 已更新过的节点的数量
      
    // 保存映射关系  
    for (let i = nextStart; i <= nextEnd; i++) {
      let key = nextChildren[i].key
      nextIndexMap[key] = i
    } 
    
    // 去旧列表找位置
    for (let i = prevStart; i <= prevEnd; i++) {
      let prevNode = prevChildren[i],
      	prevKey = prevNode.key,
        nextIndex = nextIndexMap[prevKey];
      // 新列表中没有该节点 或者 已经更新了全部的新节点，直接删除旧节点
      if (nextIndex === undefind || patched >= nextLeft) {
        parent.removeChild(prevNode.el)
        continue
      }
      // 找到对应的节点
      let nextNode = nextChildren[nextIndex];
      patch(prevNode, nextNode, parent);
      // 给source赋值
      source[nextIndex - nextStart] = i
      patched++
    }
  }
}
复制代码

找到位置后，我们观察这个重新赋值后的source，我们可以看出，如果是全新的节点的话，其在source数组中对应的值就是初始的-1，通过这一步我们可以区分出来哪个为全新的节点，哪个是可复用的。

其次，我们要判断是否需要移动。那么如何判断移动呢？很简单，和React一样我们用递增法，如果我们找到的index是一直递增的，说明不需要移动任何节点。我们通过设置一个变量来保存是否需要移动的状态。

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  outer: {
  // ...
  }
  
  // 边界情况的判断
  if (j > prevEnd && j <= nextEnd) {
    // ...
  } else if (j > nextEnd && j <= prevEnd) {
    // ...
  } else {
    let prevStart = j,
      nextStart = j,
      nextLeft = nextEnd - nextStart + 1,     // 新列表中剩余的节点长度
      source = new Array(nextLeft).fill(-1),  // 创建数组，填满-1
      nextIndexMap = {},                      // 新列表节点与index的映射
      patched = 0,
      move = false,                           // 是否移动
      lastIndex = 0;                          // 记录上一次的位置
      
    // 保存映射关系  
    for (let i = nextStart; i <= nextEnd; i++) {
      let key = nextChildren[i].key
      nextIndexMap[key] = i
    } 
    
    // 去旧列表找位置
    for (let i = prevStart; i <= prevEnd; i++) {
      let prevNode = prevChildren[i],
      	prevKey = prevNode.key,
        nextIndex = nextIndexMap[prevKey];
      // 新列表中没有该节点 或者 已经更新了全部的新节点，直接删除旧节点
      if (nextIndex === undefind || patched >= nextLeft) {
        parent.removeChild(prevNode.el)
        continue
      }
      // 找到对应的节点
      let nextNode = nextChildren[nextIndex];
      patch(prevNode, nextNode, parent);
      // 给source赋值
      source[nextIndex - nextStart] = i
      patched++
      
      // 递增方法，判断是否需要移动
      if (nextIndex < lastIndex) {
      	move = false
      } else {
      	lastIndex = nextIndex
      }
    }
    
    if (move) {
    
    // 需要移动
    } else {
	
    //不需要移动
    }
  }
}
复制代码

3. DOM如何移动

判断完是否需要移动后，我们就需要考虑如何移动了。一旦需要进行DOM移动，我们首先要做的就是找到source的最长递增子序列。

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  if (move) {
	const seq = lis(source); // [0, 1]
  // 需要移动
  } else {

  //不需要移动
  }
}
复制代码

什么是最长递增子序列：给定一个数值序列，找到它的一个子序列，并且子序列中的值是递增的，子序列中的元素在原序列中不一定连续。

例如给定数值序列为：[ 0, 8, 4, 12 ]。

那么它的最长递增子序列就是：[0, 8, 12]。

当然答案可能有多种情况，例如：[0, 4, 12] 也是可以的。

上面的代码中，我们调用lis 函数求出数组source的最长递增子序列为[ 0, 1 ]。我们知道 source 数组的值为 [2, 3, 1, -1]，很显然最长递增子序列应该是[ 2, 3 ]，但为什么计算出的结果是[ 0, 1 ]呢？其实[ 0, 1 ]代表的是最长递增子序列中的各个元素在source数组中的位置索引，如下图所示：

我们根据source，对新列表进行重新编号，并找出了最长递增子序列。

我们从后向前进行遍历source每一项。此时会出现三种情况：

1. 当前的值为-1，这说明该节点是全新的节点，又由于我们是从后向前遍历，我们直接创建好DOM节点插入到队尾就可以了。
2. 当前的索引为最长递增子序列中的值，也就是i === seq[j]，这说说明该节点不需要移动
3. 当前的索引不是最长递增子序列中的值，那么说明该DOM节点需要移动，这里也很好理解，我们也是直接将DOM节点插入到队尾就可以了，因为队尾是排好序的。

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  if (move) {
   // 需要移动
	const seq = lis(source); // [0, 1]
    let j = seq.length - 1;  // 最长子序列的指针
    // 从后向前遍历
    for (let i = nextLeft - 1； i >= 0; i--) {
      let pos = nextStart + i, // 对应新列表的index
        nextNode = nextChildren[pos],	// 找到vnode
      	nextPos = pos + 1，    // 下一个节点的位置，用于移动DOM
        refNode = nextPos >= nextChildren.length ? null : nextChildren[nextPos].el, //DOM节点
        cur = source[i];  // 当前source的值，用来判断节点是否需要移动
    
      if (cur === -1) {
        // 情况1，该节点是全新节点
      	mount(nextNode, parent, refNode)
      } else if (cur === seq[j]) {
        // 情况2，是递增子序列，该节点不需要移动
        // 让j指向下一个
        j--
      } else {
        // 情况3，不是递增子序列，该节点需要移动
        parent.insetBefore(nextNode.el, refNode)
      }
    }
 
  } else {
  //不需要移动
  
  }
}
复制代码

说完了需要移动的情况，再说说不需要移动的情况。如果不需要移动的话，我们只需要判断是否有全新的节点给他添加进去就可以了。具体代码如下：

function vue3Diff(prevChildren, nextChildren, parent) {
  //...
  if (move) {
	const seq = lis(source); // [0, 1]
    let j = seq.length - 1;  // 最长子序列的指针
    // 从后向前遍历
    for (let i = nextLeft - 1； i >= 0; i--) {
      let pos = nextStart + i, // 对应新列表的index
        nextNode = nextChildren[pos],	// 找到vnode
      	nextPos = pos + 1，    // 下一个节点的位置，用于移动DOM
        refNode = nextPos >= nextChildren.length ? null : nextChildren[nextPos].el, //DOM节点
        cur = source[i];  // 当前source的值，用来判断节点是否需要移动
    
      if (cur === -1) {
        // 情况1，该节点是全新节点
      	mount(nextNode, parent, refNode)
      } else if (cur === seq[j]) {
        // 情况2，是递增子序列，该节点不需要移动
        // 让j指向下一个
        j--
      } else {
        // 情况3，不是递增子序列，该节点需要移动
        parent.insetBefore(nextNode.el, refNode)
      }
    }
  } else {
    //不需要移动
    for (let i = nextLeft - 1； i >= 0; i--) {
      let cur = source[i];  // 当前source的值，用来判断节点是否需要移动
    
      if (cur === -1) {
       let pos = nextStart + i, // 对应新列表的index
          nextNode = nextChildren[pos],	// 找到vnode
          nextPos = pos + 1，    // 下一个节点的位置，用于移动DOM
          refNode = nextPos >= nextChildren.length ? null : nextChildren[nextPos].el, //DOM节点
      	mount(nextNode, parent, refNode)
      }
    }
  }
}
复制代码

至此vue3.0的diff完成。

4. 最长递增子序列

leetcode有原题，官方解析很清晰，看不懂我讲的可以去看看官方解析。

我们以该数组为例

[10,9,2,5,3,8,7,13]

我们可以使用动态规划的思想考虑这个问题。动态规划的思想是将一个大的问题分解成多个小的子问题，并尝试得到这些子问题的最优解，子问题的最优解有可能会在更大的问题中被利用，这样通过小问题的最优解最终求得大问题的最优解。

我们先假设只有一个值的数组[13]，那么该数组的最长递增子序列就是[13]自己本身，其长度为1。那么我们认为每一项的递增序列的长度值均为1

那么我们这次给数组增加一个值[7, 13], 由于7 < 13，所以该数组的最长递增子序列是[7, 13]，那么该长度为2。那么我们是否可以认为，当[7]小于[13]时，以[7]为头的递增序列的长度是，[7]的长度和[13]的长度的和，即1 + 1 = 2。

ok，我们基于这种思想来给计算一下该数组。我们先将每个值的初始赋值为1

首先 7 < 13 那么7对应的长度就是13的长度再加1，1 + 1 = 2

继续，我们对比8。我们首先和7比，发现不满足递增，但是没关系我们还可以继续和13比，8 < 13满足递增，那么8的长度也是13的长度在加一，长度为2

我们再对比3，我们先让其与8进行对比，3 < 8，那么3的长度是8的长度加一，此时3的长度为3。但是还没结束，我们还需要让3与7对比。同样3 < 7，此时我们需要在计算出一个长度是7的长度加一同样是3，我们对比两个长度，如果原本的长度没有本次计算出的长度值大的话，我们进行替换，反之则我们保留原本的值。由于3 === 3，我们选择不替换。最后，我们让3与13进行对比，同样的3 < 13，此时计算出的长度为2，比原本的长度3要小，我们选择保留原本的值。

之后的计算依次类推，最后的结果是这样的

我们从中取最大的值4，该值代表的最长递增子序列的个数。代码如下：

function lis(arr) {
  let len = arr.length,
    dp = new Array(len).fill(1); // 用于保存长度
  for (let i = len - 1; i >= 0; i--) {
    let cur = arr[i]
    for(let j = i + 1; j < len; j++) {
      let next = arr[j]
      // 如果是递增 取更大的长度值
      if (cur < next) dp[i] = Math.max(dp[j]+1, dp[i])
    }
  }
  return Math.max(...dp)
}

至此为止，我们讲完了基础的最长递增子序列。然而在vue3.0中，我们需要的是最长递增子序列在原本数组中的索引。所以我们还需要在创建一个数组用于保存每个值的最长子序列所对应在数组中的index。具体代码如下：

function lis(arr) {
  let len = arr.length,
    res = [],
    dp = new Array(len).fill(1);
  // 存默认index
  for (let i = 0; i < len; i++) {
    res.push([i])
  }
  for (let i = len - 1; i >= 0; i--) {
    let cur = arr[i],
      nextIndex = undefined;
    // 如果为-1 直接跳过，因为-1代表的是新节点，不需要进行排序
    if (cur === -1) continue
    for (let j = i + 1; j < len; j++) {
      let next = arr[j]
      // 满足递增条件
      if (cur < next) {
        let max = dp[j] + 1
        // 当前长度是否比原本的长度要大
        if (max > dp[i]) {
          dp[i] = max
          nextIndex = j
        }
      }
    }
    // 记录满足条件的值，对应在数组中的index
    if (nextIndex !== undefined) res[i].push(...res[nextIndex])
  }
  let index = dp.reduce((prev, cur, i, arr) => cur > arr[prev] ? i : prev, dp.length - 1)
  // 返回最长的递增子序列的index
  return result[index]
}

为什么不要以index作为key？

1key的作用

在我们上述diff算法中，通过isSameVNodeType方法判断，来判断key是否相等判断新老节点。

那么由此我们可以总结出？

在v-for循环中，key的作用是：通过判断newVnode和OldVnode的key是否相等，从而复用与新节点对应的老节点，节约性能的开销。

2如何正确使用key

①错误用法 1：用index做key。

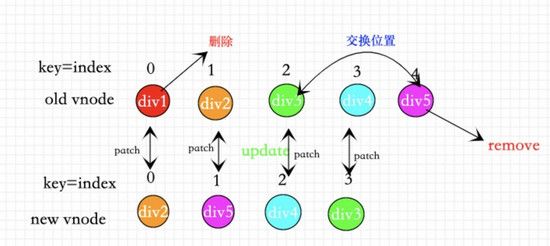
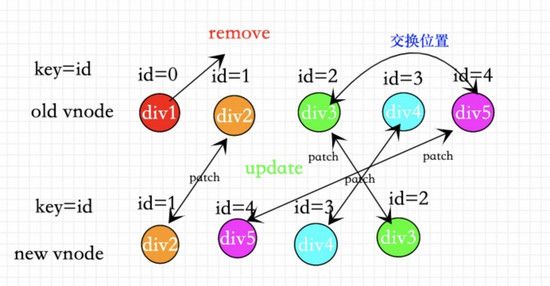
用index做key的效果实际和没有用diff算法是一样的，为什么这么说呢，下面我就用一幅图来说明：

如果所示当我们用index作为key的时候，无论我们怎么样移动删除节点，到了diff算法中都会从头到尾依次patch(图中： 所有节点均未有效的复用 )

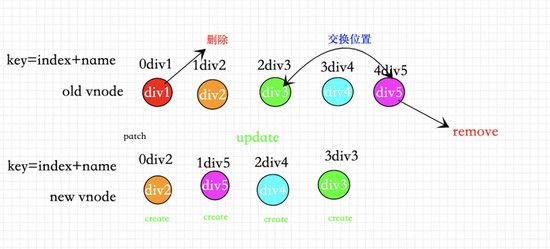
②错误用法2 ：用index拼接其他值作为key。

当已用index拼接其他值作为索引的时候，因为每一个节点都找不到对应的key，导致所有的节点都不能复用,所有的新vnode都需要重新创建。都需要重新create

如图所示。

③正确用法 ：用唯一值id做key(我们可以用前后端交互的数据源的id为key)。

如图所示。每一个节点都做到了复用。起到了diff算法的真正作用。

节点reverse场景

假设我们有这样的一段代码：

    <div id="app">
      <ul>
        <item
          :key="index"
          v-for="(num, index) in nums"
          :num="num"
          :class="`item${num}`"
        ></item>
      </ul>
      <button @click="change">改变</button>
    </div>
    <script src="./vue.js"></script>
    <script>
      var vm = new Vue({
        name: "parent",
        el: "#app",
        data: {
          nums: [1, 2, 3]
        },
        methods: {
          change() {
            this.nums.reverse();
          }
        },
        components: {
          item: {
            props: ["num"],
            template: `
                    

                       {{num}}
                    
                `,
            name: "child"
          }
        }
      });
    </script>
复制代码

其实是一个很简单的列表组件，渲染出来 1 2 3 三个数字。我们先以 index 作为key，来跟踪一下它的更新。

我们接下来只关注 item 列表节点的更新，在首次渲染的时候，我们的虚拟节点列表 oldChildren 粗略表示是这样的：

[
  {
    tag: "item",
    key: 0,
    props: {
      num: 1
    }
  },
  {
    tag: "item",
    key: 1,
    props: {
      num: 2
    }
  },
  {
    tag: "item",
    key: 2,
    props: {
      num: 3
    }
  }
];
复制代码

在我们点击按钮的时候，会对数组做 reverse 的操作。那么我们此时生成的 newChildren 列表是这样的：

[
  {
    tag: "item",
    key: 0,
    props: {
+     num: 3
    }
  },
  {
    tag: "item",
    key: 1,
    props: {
+     num: 2
    }
  },
  {
    tag: "item",
    key: 2,
    props: {
+     num: 1
    }
  }
];
复制代码

发现什么问题没有？key的顺序没变，传入的值完全变了。这会导致一个什么问题？

本来按照最合理的逻辑来说，旧的第一个vnode 是应该直接完全复用 新的第三个vnode的，因为它们本来就应该是同一个vnode，自然所有的属性都是相同的。

但是在进行子节点的 diff 过程中，会在 旧首节点和新首节点用sameNode对比。 这一步命中逻辑，因为现在新旧两次首部节点 的 key 都是 0了，

然后把旧的节点中的第一个 vnode 和 新的节点中的第一个 vnode 进行 patchVnode 操作。

这会发生什么呢？我可以大致给你列一下： 首先，正如我之前的文章props的更新如何触发重渲染？里所说，在进行 patchVnode 的时候，会去检查 props 有没有变更，如果有的话，会通过 _props.num = 3 这样的逻辑去更新这个响应式的值，触发 dep.notify，触发子组件视图的重新渲染等一套很重的逻辑。

然后，还会额外的触发以下几个钩子，假设我们的组件上定义了一些dom的属性或者类名、样式、指令，那么都会被全量的更新。

1. updateAttrs
2. updateClass
3. updateDOMListeners
4. updateDOMProps
5. updateStyle
6. updateDirectives

而这些所有重量级的操作（虚拟dom发明的其中一个目的不就是为了减少真实dom的操作么？），都可以通过直接复用 第三个vnode 来避免，是因为我们偷懒写了 index 作为 key，而导致所有的优化失效了。

节点删除场景

另外，除了会导致性能损耗以外，在删除子节点的场景下还会造成更严重的错误，

假设我们有这样的一段代码：

<body>
  <div id="app">
    <ul>
      <li v-for="(value, index) in arr" :key="index">
        <test />
      </li>
    </ul>
    <button @click="handleDelete">delete</button>
  </div>
  </div>
</body>
<script>
  new Vue({
    name: "App",
    el: '#app',
    data() {
      return {
        arr: [1, 2, 3]
      };
    },
    methods: {
      handleDelete() {
        this.arr.splice(0, 1);
      }
    },
    components: {
      test: {
        template: "
{{Math.random()}}
"
      }
    }
  })
</script>
复制代码

那么一开始的 vnode列表是：

[
  {
    tag: "li",
    key: 0,
    // 这里其实子组件对应的是第一个 假设子组件的text是1
  },
  {
    tag: "li",
    key: 1,
    // 这里其实子组件对应的是第二个 假设子组件的text是2
  },
  {
    tag: "li",
    key: 2,
    // 这里其实子组件对应的是第三个 假设子组件的text是3
  }
];
复制代码

有一个细节需要注意，为什么说 Vue 的响应式更新比 React 快？，Vue 对于组件的 diff 是不关心子组件内部实现的，它只会看你在模板上声明的传递给子组件的一些属性是否有更新。

也就是和v-for平级的那部分，回顾一下判断 sameNode 的时候，只会判断key、 tag、是否有data的存在（不关心内部具体的值）、是否是注释节点、是否是相同的input type，来判断是否可以复用这个节点。

<li v-for="(value, index) in arr" :key="index"> // 这里声明的属性
  <test />
</li>
复制代码

有了这些前置知识以后，我们来看看，点击删除子元素后，vnode 列表 变成什么样了。

[
  // 第一个被删了
  {
    tag: "li",
    key: 0,
    // 这里其实上一轮子组件对应的是第二个 假设子组件的text是2
  },
  {
    tag: "li",
    key: 1,
    // 这里其实子组件对应的是第三个 假设子组件的text是3
  },
];
复制代码

虽然在注释里我们自己清楚的知道，第一个 vnode 被删除了，但是对于 Vue 来说，它是感知不到子组件里面到底是什么样的实现（它不会深入子组件去对比文本内容），那么这时候 Vue 会怎么 patch 呢？

由于对应的 key使用了 index导致的错乱，它会把

1. 原来的第一个节点text: 1直接复用。
2. 原来的第二个节点text: 2直接复用。
3. 然后发现新节点里少了一个，直接把多出来的第三个节点text: 3 丢掉。

至此为止，我们本应该把 text: 1节点删掉，然后text: 2、text: 3 节点复用，就变成了错误的把 text: 3 节点给删掉了。

为什么不要用随机数作为key？

<item
  :key="Math.random()"
  v-for="(num, index) in nums"
  :num="num"
  :class="`item${num}`"
/>
复制代码

其实我听过一种说法，既然官方要求一个 唯一的key，是不是可以用 Math.random() 作为 key 来偷懒？这是一个很鸡贼的想法，看看会发生什么吧。

首先 oldVnode 是这样的：

[
  {
    tag: "item",
    key: 0.6330715699108844,
    props: {
      num: 1
    }
  },
  {
    tag: "item",
    key: 0.25104533240710514,
    props: {
      num: 2
    }
  },
  {
    tag: "item",
    key: 0.4114769152411637,
    props: {
      num: 3
    }
  }
];
复制代码

更新以后是：

[
  {
    tag: "item",
+   key: 0.11046018699748683,
    props: {
+     num: 3
    }
  },
  {
    tag: "item",
+   key: 0.8549799545696619,
    props: {
+     num: 2
    }
  },
  {
    tag: "item",
+   key: 0.18674467938937478,
    props: {
+     num: 1
    }
  }
];

复制代码

可以看到，key 变成了完全全新的 3 个随机数。

上面说到，diff 子节点的首尾对比如果都没有命中，就会进入 key 的详细对比过程，简单来说，就是利用旧节点的 key -> index 的关系建立一个 map 映射表，然后用新节点的 key 去匹配，如果没找到的话，就会调用 createElm 方法 重新建立 一个新节点。

具体代码在这：

// 建立旧节点的 key -> index 映射表
oldKeyToIdx = createKeyToOldIdx(oldCh, oldStartIdx, oldEndIdx);

// 去映射表里找可以复用的 index
idxInOld = findIdxInOld(newStartVnode, oldCh, oldStartIdx, oldEndIdx);
// 一定是找不到的，因为新节点的 key 是随机生成的。
if (isUndef(idxInOld)) {
  // 完全通过 vnode 新建一个真实的子节点
  createElm();
}
复制代码

也就是说，咱们的这个更新过程可以这样描述： 123 -> 前面重新创建三个子组件 -> 321123 -> 删除、销毁后面三个子组件 -> 321。

发现问题了吧？这是毁灭性的灾难，创建新的组件和销毁组件的成本你们晓得的伐……本来仅仅是对组件移动位置就可以完成的更新，被我们毁成这样了。

总结

经过这样的一段旅行，diff 这个庞大的过程就结束了。

我们收获了什么？

1. 用组件唯一的 id（一般由后端返回）作为它的 key，实在没有的情况下，可以在获取到列表的时候通过某种规则为它们创建一个 key，并保证这个 key 在组件整个生命周期中都保持稳定。
2. 如果你的列表顺序会改变，别用 index 作为 key，和没写基本上没区别，因为不管你数组的顺序怎么颠倒，index 都是 0, 1, 2 这样排列，导致 Vue 会复用错误的旧子节点，做很多额外的工作。列表顺序不变也尽量别用，可能会误导新人。
3. 千万别用随机数作为 key，不然旧节点会被全部删掉，新节点重新创建，你的老板会被你气死。

既然 index 只是在某些特定的场景下会出问题，那 列表顺序保持不变 的情况下还是可以接着用。这样做有什么问题呢？

1. 团队代码规范，假设这样一个场景吧，你这边代码里全部写的 :key="index"，有一个新人入职了跟着写，结果他的场景是删除和乱序的，这种情况你一个个讲原理指正？这就是统一代码规范和最佳实践的作用啊。eslint 甚至也专门有一个 rule 叫做 react/no-array-index-key，为什么要有这些约束和规范？如果社区总结了最佳实践，为什么一定要去打破它？这都是值得思考的。 就像 == 操作符，为什么要禁止？就是因为隐式转换会出很多问题，你说你熟背隐式转换所有原理，你能保证团队所有小伙伴都熟背？何苦有更简单的 === 操作符可以用。
2. 说开发效率的问题，index 作为 key 我在上面已经提到了好几种会出问题的情况了，还是坚持要用，就因为简单。那么 TypeScript 也没有火起来的必要吗？它需要多写很多代码，“效率” 很低，为什么它火了？不是因为用 JavaScript 就一定会出现类型错误，而是因为用了 TypeScript 可以更好的保证你代码的稳定性。正如用了 id 作为key，可以比 index 更好的保证稳定性，更何况用 id 也不费事啊。完全都不像 TypeScript 带来的额外的语法成本。
3. 所谓的列表顺序稳定，这个稳定你真的能保证吗？除了你前端写死的永远不变的一个列表，就假设你的列表没有在头部新增一项（导致节点全部依次错误复用），在任意位置 删除一项（有时导致错误删除）等这些会导致 patch 过程出现问题的操作。 就举个很简单的例子，你的“静态”列表的顺序是[1, 2, 3]，数据库里突然加入了一条新数据0，那么你认为的不会变的列表的就变成了[0, 1, 2, 3]。然后，1 节点就错误的和 0节点进行 patchVnode， 2 节点就错误的和 1 节点进行 patch、导致原本只需要把新增的0节点插入到头部，然后分别对 1 -> 1、2 -> 2、3 -> 3 进行 patchVnode即可（基本没有变化），变成了毁灭的全量更新。（如果子组件是个很重的组件呢？它的每一项都会经历完整的 vm._update(vm._render())）过程，因为 props 变了。

那么 当面试官问到 讲讲vue的diff算法的时候，应该怎么回答呢？

首先，我们拿到新旧节点的数组，然后初始化四个指针，分别指向新旧节点的开始位置和结束位置，进行两两对比，若是 新的开始节点和旧开始节点相同，则都向后面移动，若是结尾节点相匹配，则都前移指针。若是新开始节点和旧结尾节点匹配上了，则会将旧的结束节点移动到旧的开始节点前。若是旧开始节点和新的结束节点相匹配，则会将旧开始节点移动到旧结束节点的后面。若是上述节点都没配有匹配上，则会进行一个兜底逻辑的判断，判断开始节点是否在旧节点中，若是存在则复用，若是不存在则创建。最终跳出循环，进行裁剪或者新增，若是旧的开始节点小于旧的结束节点，则会删除之间的节点，反之则是新增新的开始节点到新的结束节点。

微任务：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RcW9JyHr-1646741202856)(虚拟DOM和diff算法.assets/image-20220308190556444.png)]