利用特征值与特征向量求解弹性力学中的主应力与主平面问题

---

前言

已知物体在任意一点的六个应力分量$({\sigma }_x,{\sigma }_y,{\sigma }_z,{\tau }_{yz},{\tau }_{zx},{\tau }_{xy})$,求解该点的主应力与主平面方向一直是力学研究领域的热点话题。目前一些常见的方法为$代数法、莫尔圆法$，前者结果直观但需经过严密的数学推导，后者不失为一种简单快捷的方法。考虑到平衡方程以及几何关系的特殊性，我们可以对平衡方程进行取行列式求解得到相应的特征值与特征向量，$该特征值与特征值所对应特征向量分别为该点处的主应力及其主平面$。

---

一、二向应力状态

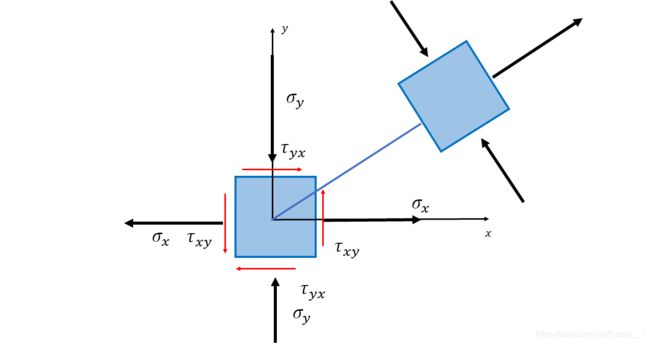
如下图所示，在受力构件中取出一点的单元体，其为二向应力状态的一般情况，由于是平面应力状态,可简化成右图所示，其中${\sigma }_x,{\sigma }_y,{\tau }_{xy}$ 为已知。

对该平面微元体，先假设任意斜截面，其法线与$x$轴夹角为$\alpha$。规定由$x$轴逆时针转向$n$为正。设微元体为单位厚度，斜截面的面积为$dA$。
下面对微元体建立水平方向和竖直方向上平衡方程，令$cos\alpha =l,sin\alpha =m$得：

$$l{\sigma }_x+m{\tau }_{xy}=p_x\text{\hspace{1em}(1)}$$
$$m{\sigma }_y+l{\tau }_{xy}=p_y\text{\hspace{1em}(2)}$$
其中:
$$p_x={\sigma }_{N}l+{\tau }_{N}m\text{\hspace{1em}(3)}$$
$$p_y={\sigma }_{N}m+{\tau }_{N}l\text{\hspace{1em}(4)}$$.
通过这四个方程，我们理论上可以解出任意角度斜截面上的正应力与切应力分布，为：

$${\sigma }_{\alpha }=\frac{{\sigma }_x+{\sigma }_y}{2}+\frac{{\sigma }_x-{\sigma }_y}{2}(2l^2-1)-2{\tau }_{xy}ml\text{\hspace{1em}(5)}$$

$${\tau }_{\alpha }=({\sigma }_x-{\sigma }_y)lm+{\tau }_{xy}(2l^2-1)\text{\hspace{1em}(6)}$$

但这些并不是我们所想要的,我们需要的是建立主应力与3个已知应力分量得关系式。
现在我们先交代一下主应力概念：
设经过任意一点$P$的某一斜面上的切应力等于零，则该斜面上的正应力成为$P$点的一个主应力，该斜面称为在$P$的一个应力主面，该斜面的法线方向称为在$P$点的一个应力主向。
简单地，当这种主应力存在时，${\tau }_N=0$,即该斜面上应力在坐标轴上的投影变为：
$$p_x={\sigma }_{N}l\text{\hspace{1em}(7)}$$
$$p_y={\sigma }_{N}m\text{\hspace{1em}(8)}$$.
将以上两个式子带入$(1)、(2)$得：
$$l{\sigma }_x+m{\tau }_{xy}={\sigma }_{N}l\text{\hspace{1em}(9)}$$
$$m{\sigma }_y+l{\tau }_{xy}={\sigma }_{N}m\text{\hspace{1em}(10)}$$
整理$(9)、(10)$得：
$$({\sigma }_x-{\sigma }_N)l+{\tau }_{xy}m=0\text{\hspace{1em}(11)}$$
$${\tau }_{xy}l+({\sigma }_y-{\sigma }_N)m=0\text{\hspace{1em}(12)}$$
注意到：$l^2+m^2=1$，将$(11)、(12)$方程组看作是以$l、m$为未知量，于是该方程组有非零解

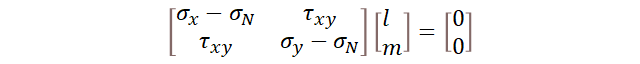
则:

问题进行到这一步，先回顾一下线性代数中特征值与特征向量的概念：
几乎所有的向量在乘以矩阵$A$后都会改变方向，某些特殊的向量$x$和$Ax$位于同一个方向，它们称之为特征向量。

$Ax=\lambda x$

数字$\lambda$称为特征值。它告诉我们在乘以$A$后，向量是怎么被拉伸、缩小、反转或者不变的。$\lambda =0$意味着特征向量存在于矩阵的零空间中。任意向量都是单位矩阵的特征向量，因为$Ix=1$，其特征值为 1。

要计算特征值的话，我们只需要知道$A-\lambda I$即可。
将所求的$\lambda$带回$Ax=\lambda x$中将求得特征向量$x$。
分析可知，$A=\left[\begin{array}{cc}{\sigma }_x& {\tau }_{xy}\\ {\tau }_{xy}& {\sigma }_y\end{array}\right]$,$求{\sigma }_N的过程就是求A特征值的过程。$
计算机较普遍的求特征值的算法为QR分解以及Jacobi旋转，在此我将附上QR分解的VB程序。jacobi旋转法参见jacobi旋转法的VB实现。
由于$A为2\times 2阶$,故所求的特征值为2重。

例：已知单元体${\sigma }_x=80MPa,{\sigma }_y=-40MPa,{\tau }_{xy}=-60MPa$,试求主应力，并确定主平面方向。

1. 莫尔圆图解法

在此，为复习之前的莫尔圆，我将先采用应力图解法求解：
根据${\left({\sigma }_{\alpha }-\frac{{\sigma }_x+{\sigma }_y}{2}\right)}^2+{\tau }_{\alpha }^2={\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2$可知若以$\sigma 、\tau$为横纵坐标，则圆心的坐标为$\left(\frac{{\sigma }_x+{\sigma }_y}{2},0\right)$,圆周半径为$\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_y}{2}\right)}^2+{\tau }_{xy}^2}$

根据应力圆与微元体角度的2倍关系，在单元体上从$x轴以逆时针方向量取\frac{\alpha }{2}=22.5°，A、B对应的横坐标值分别为该单元体的最大主应力和最小主应力。$

2. 特征值与特征向量解法

建立矩阵
$A=\left[\begin{array}{cc}{\sigma }_x& {\tau }_{xy}\\ {\tau }_{xy}& {\sigma }_y\end{array}\right]=\left[\begin{array}{cc}80& 60\\ 60& -40\end{array}\right]$
这里我们采用MATLAB进行矩阵特征值及其特征根的计算：
$[V,D]=eig(A)$
返回特征值的对角矩阵 $D$ 和矩阵$V$，其列是对应的右特征向量，使得 $A\ast V=V\ast D$。
计算结果：$\lambda 1=-64.8528,\lambda 2=104.8528$,即
${\sigma }_1=104.8528MPa,{\sigma }_2=-64.8528MPa$

对应特征向量：$m1=\left[\begin{array}{c}0.3827\\ -0.9239\end{array}\right],m2=\left[\begin{array}{c}-0.9239\\ -0.3827\end{array}\right]$分别对应两个主平面的方向余弦。
同样地道理，当我们需要求解最大切应力和最小切应力时（即该法平面内只存在切应力${\tau }_N,无正应力{\sigma }_N)$这里将有部分证明过程 ，我们可将
$$p_x={\sigma }_{N}l\text{\hspace{1em}(7)}$$
$$p_y={\sigma }_{N}m\text{\hspace{1em}(8)}$$.中的$m和n置换$得到最大切应力及其方向，这里将不再重复。结论：在应力圆上，从主平面A点逆时针最（顺时针）转圆心角90°到C（D）点，在单元体上从${\sigma }_1$逆时针（顺时针）转45°可得最大（最小）切应力。

二、三向应力状态

推广一个更一般的情况，从空间中任意一点取出的单元体如下：

可见，微元体三个方向上均不同程度地作用着应力，当这种应力状态变成主应力状态时，三个主应力均不为0。
依据张量分析（将会在另一篇博客里面做一些分析），我们可以较为快捷的得出任意斜截面三棱锥的应力分布，列写三个方向上的平衡方程：
$$l{\sigma }_x+m{\tau }_{xy}+n{\tau }_{zx}=l{\sigma }_N\text{\hspace{1em}(13)}$$
$$m{\sigma }_y+n{\tau }_{zy}+l{\tau }_{xy}=m{\sigma }_N\text{\hspace{1em}(14)}$$
$$n{\sigma }_z+l{\tau }_{xz}+m{\tau }_{yz}=n{\sigma }_N\text{\hspace{1em}(15)}$$
列出的实对称阵为：

$A=\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{yx}& {\tau }_{zx}\\ {\tau }_{xy}& {\sigma }_y& {\tau }_{zy}\\ {\tau }_{xz}& {\tau }_{yz}& {\sigma }_z\end{array}\right]$
于是，对应3重主应力为：

$\sigma =\left[\begin{array}{ccc}{\sigma }_1& {\sigma }_2& {\sigma }_3\end{array}\right]=\left[\begin{array}{ccc}{\lambda }_1& {\lambda }_2& {\lambda }_3\end{array}\right]$

对应3重主方向为：

$x=\left[\begin{array}{ccc}{l}_1& l_2& l_3\\ m_1& m_2& m_3\\ n_1& n_2& n_3\end{array}\right]$

求解如图三向应力状态的主应力：

采用计算机求解特征值与特征向量：

A=[70 50 0;50 0 0;0 0 60];
>> [x,y]=eig(A)
>x =

    0.4618         0   -0.8870
   -0.8870         0   -0.4618
         0    1.0000         0


y =

  -26.0328         0         0
         0   60.0000         0
         0         0   96.0328