shape from shading

一.shape from X　算法

  定义：从单目二维图像恢复三维信息的技术.其中，X可以是光度立体（stereo）、运动（motion）、纹理（texture）和阴影（shading）．具体分类如下：

１．从光度立体恢复形状的方法(Shape from Photometric Stereo)
  原理：从一系列不同光照条件下采集的图像中恢复场景中目标表面朝向（即梯度（p，q））的方法。

２．从运动恢复形状的方法(Shape from Motion，SFM)
  原理：目标在相机前运动或相机在一个固定的环境中运动时，所获得的图像变化可用来恢复相机和目标间的相对运动以及场景中多个目标间的相互关系。

３．从纹理与表面朝向恢复形状的方法(Shape from Texture)
  原理：利用物体表面上的纹理可以确定表面朝向，进而恢复表面形状．

４．从阴影恢复形状的方法(Shape from Shading)
  原理：利用成像表面亮度的变化，解析出物体表面的矢量信息，从而转换为表面深度信息．

二.shape from shading(SFS)　算法

2.1 SFS问题的起源

  理想的SFS问题是基于朗伯体光照模型的，即进行了如下假设。
1）光源为无限远处的点光源，或者均匀照明的平行光。
2）成像几何关系为正交投影。
3）物体表面为理想散射表面。从所有方向观察，它都是同样的亮度，并且完全反射所有入射光。

  在朗伯体假设下，物体表面点的图像亮度E仅由该点光源入射角的余弦决定。但是即使在满足朗伯体反射模型且已知光源方向的前提下，若将形状表示成表面法向量，那么就会得到一个含有三个未知量nx、ny、nz的线性方程；若表示成表面梯度，则会得到一个含有两个未知量p、q的非线性方程。

  采集图像的灰度与四个因素有关：
1）物体可见表面的几何形状。
2）光源的入射强度和方向。
3）观察者相对物体的方位和距离。
4）物体表面的反射特性。

  假设沿观察者方向的视线与成像的XY平面垂直相交，设梯度坐标系PQ与像平面坐标系EXY重合。设光源的强度为I（x，y），光源向量为（pi，qi，-1），物体表面法向量为（p，q，-1），角度θ为光源矢量与表面法向量的夹角，则法向量N的反射强度可表示为:
在内积空间中，任意两个非零向量x与y的夹角α的余弦为
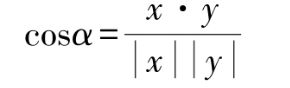那么入射光与表面法向量夹角θ的余弦可表示为
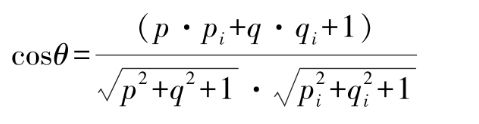则图像灰度可以表示为

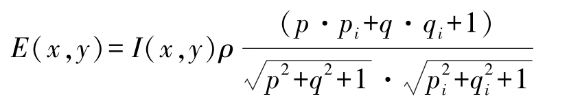
  根据上公式可知，当光源入射方向（pi，qi）与物体表面法向量方向（p，q）相同时，两者夹角θ的余弦函数取值为1，根据公式可知此时获得的图像灰度E（x，y）值最大，即该点为图像亮度最大值点。由此可以得到一个重要结论：图像中最亮点的表面法向量指向光源方向。
  在E（x，y）、I（x，y）、ρ、（pi，qi）已知的情况下，上式为含有两个未知量p，q的非线性方程。如果不引入附加约束，SFS问题就是一个病态的问题，没有唯一解。

2.2 SFS问题的解决方案

  为了解决SFS问题中待求参数比方程个数多的问题，必须引入其他的约束条件，如亮度约束、光滑性约束、可积性约束、亮度梯度约束、单位法向量约束等。各约束的能量函数表达如下所述。
亮度约束：假设反射函数的亮度R与实际摄得的图像亮度I相等。即

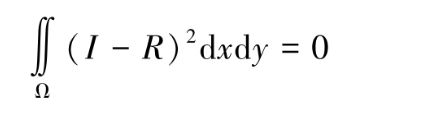
光滑性约束：假设物体表面是光滑的，那么相邻点法向量方向接近。

可积性约束：要求Z=f（x，y）的两个两阶混合偏导数相等，即

可积性约束可以描述为

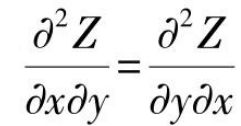
式中，Zx和Zy分别为Z关于x和y的偏导数。

亮度梯度约束：亮度约束是保证理论亮度与实际摄得亮度尽量接近，而亮度梯度约束对理论亮度及实际亮度分别求x方向和y方向导数，即恢复图像的亮度梯度值与输入图像的亮度梯度值相等，即

单位法向量约束：令恢复表面的法向量为单位向量，即

  将约束方程写入能量函数。由于封闭边缘处的梯度值至少有一项是无穷大，为了保证收敛性，一般要为封闭边缘处的形状设定初值。
  常用的SFS技术可以分为四类：最小值方法（Minimization）、演化方法（Propagation）、局部分析法（Local）和线性化方法（Linear）。

2.3 最小值方法

  最小值方法即最小化能量函数。根据多元函数极值法中条件极值的求解方法，Horn等人将光滑性、可积性约束引入能量方程，利用拉格朗日乘数法构造辅助函数，即

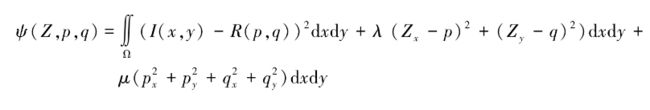
式中，λ和μ均为拉格朗日乘子。
  对上述泛函求变分，得到极值存在的必要条件为偏微分方程组成立，即

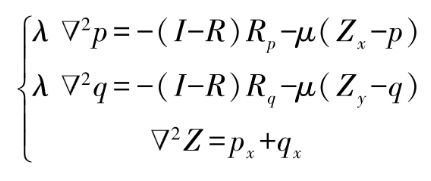
式中，▽2为拉普拉斯算子（也可以用符号Δ表示）。应用交错网格方法将p，q，Z，px，py，Zx，Zy，以及▽2算子离散化，得到离散方程组，再使用高斯-赛德尔迭代方法，同时求得物体表面梯度和表面高度的网格点值。

此方法是最早使用的SFS方法，需要输入灰度图及初始边线图，还需要输入λ及E值，操作比较复杂。

2.4 演化方法

  Horn等人提出的特征线法本质上就是一种演化方法。如果已知特征线上起始点的表面高度和表面朝向，那么图像中沿特征线的所有表面高度和朝向都可以计算。在奇点（图像中灰度值最大点）周围以球形逼近法构造初始表面曲线。在相邻特征线没有交叉的情况下，特征线不断向外演化，特征线的方向作为亮度梯度方向。如果相邻特征线间隔较远，则为了得到更详细的形状图，可以采用内插值法获得新的特征线。
  Rouy和Tourin提出一种基于Hamilton-Jacobi-Bellman等式和粘性解理论获得唯一解的SFS方法，通过动态规划建立粘性解与最优控制解之间的联系，而且可以提供连续光滑表面存在的条件。
  Oliensis采用从奇点开始恢复形状的方法来取代从封闭边缘开始的方法。基于此方法，Dupuis和Oliensis通过数值方法确定了最优SFS方法。Bichsel和Pentland简化了Dupuis和Oliensis的方法，采用最小下山法，可以将SFS的收敛控制在10次迭代以内。

  类似于Horn和Dupuis-Oliensis方法，Kimmel和Bruckstein从初始的封闭曲线通过等高线恢复表面形状。该方法使用图线奇点区域的封闭曲线作为起点，运用微分几何、流体动力学、数值分析等方法，实现了非光滑表面的恢复。
  Bichsel和Pentland给定图像奇点处的深度值，然后从8个独立的方向找出远离光源的所有点。由于图像中亮度最小的区域在多个方向的斜率接近于零（除了与照明方向窄角的情况），所以图像首先旋转，使得光源方向在图像上的投影与8个方向中的某一个一致。高度计算完毕后，再将图像反转回原来的位置，即可得到原位置上与图像点所对应的表面点高度。

2.5 局部分析方法

  局部分析法通过对物体表面进行局部形状假设来获得表面形状。
  Pentland局部分析法在假设物体表面任意点局部都是球形的情况下，通过亮度及其一阶和二阶导数恢复形状信息。Lee和Rosenfeld也是在局部球形假设的前提下，通过亮度的一阶导数在光源坐标系统中计算物体表面倾角和偏角的。
  在局部球形假设的前提下，首先在光源坐标系统中计算物体表面倾角和偏角，然后再将其转换到图像坐标系。
  如果表面反射均匀，并且反射图可以表示为：I=ρN·S，那么图像中最亮点的表面法向量指向光源方向，而且，倾角的余弦可以通过亮度的比率及反射系数ρ获得。
  Lee-Rosenfeld方法的主体实现过程为：首先找到图像中的奇点，通过图像坐标系的旋转使得图像的x轴与光源方向在图像平面上的投影一致。
旋转矩阵R为:

在该坐标系下计算表面点的倾角和偏角，然后再将所得结果转换至原图像坐标系即可。该方法是对Pentland方法的改进，省去了二阶导数的求解，可以有效预防噪声。

2.6 线性化方法

线性化方法通过对反射图进行线性化将非线性问题简化为线性问题。该方法是在反射函数中低阶项占主导作用的假设下实现的。

2.6.1 Pentland方法

Pentland以表面梯度（p，q）为变量来对反射函数线性化。反射函数可以表示为
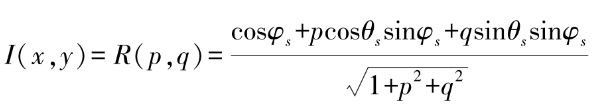式中，φs、θs分别为光源的倾角和偏角。在（p0，q0）点进行泰勒级数展开，得到
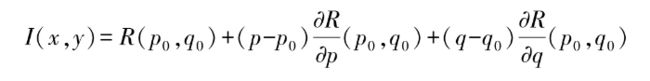对于朗伯体反射模型，p0=q0=0，所以反射函数简化为
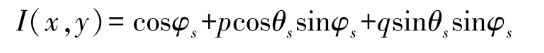两边进行傅里叶变换，根据傅里叶变换的微分性质可知
式中，FZ为Z（x，y）的傅里叶变换，（ω1，ω2）为与（p，q）对应的傅里叶变量。由此，反射函数转换为傅里叶变换形式为
式中，FI为图像亮度的傅里叶变换。从式计算得到FZ后，再通过傅里叶反变换即可得到高度值。
线性化方法不需要迭代，是个闭环解决方案，但是当反射函数中的非线性项比较大时，此法的误差比较大。

2.6.2 Tsai-Shah法

Tsai和Shah对于漫反射表面和光滑表面都做了一定的研究。他们为了线性化反射函数中的高度值Z，采用有限差分方法离散p、q，将发射函数表示为
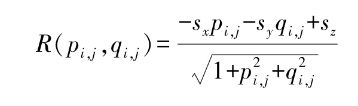使用雅可比迭代法将所有点的Z（xi，yj）0=0，得到如下公式
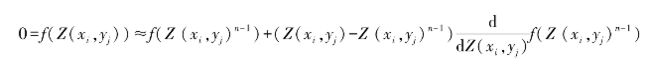在雅可比迭代中，第n层的深度可以表示为
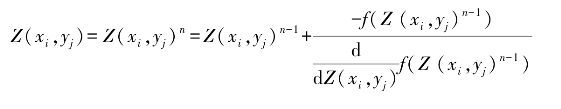其中
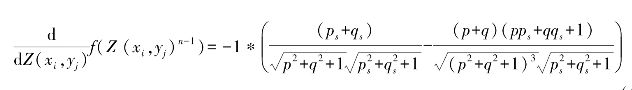Tsai-Shah方法不需要矩阵翻转，是一个简单有效的方法，但是对于图像中存在阴影效果的图形不适用。

2.6.3 Tsai-Shah法和Pentland法的比较

Pentland以表面梯度（p，q）为变量来对反射函数进行线性化，然后对反射函数进行泰勒级数展开，再通过傅里叶变换和反傅里叶变换得到高度。Tsai和Shah将（p、q）表示为高度Z的离散逼近形式。Tsai-Shah法的优势在于以下几个方面。

1）对Z进行线性化优于对（p，q）进行线性化。2）当光源方向与观察方向相近时，梯度（p，q）的二次项将在反射函数中占据很大比重。Pentland方法使用傅里叶变换时，p2和q2会产生双重作用。Tsai-Shah法没有使用傅里叶变换，所以没有频率的双重效果。3）时间短，不需要傅里叶变换和反傅里叶变换。

参考书籍<<机器视觉与机器学习　算法原理,框架应用与代码实现>>