小酒馆燃着灯

第十一章目标检测中的NMS

精度提升

众所周知，非极大值抑制NMS是目标检测常用的后处理算法，用于剔除冗余检测框，本文将对可以提升精度的各种NMS方法及其变体进行阶段性总结。

总体概要：

对NMS进行分类，大致可分为以下六种，这里是依据它们在各自论文中的核心论点进行分类，这些算法可以同时属于多种类别。

分类优先：传统NMS，Soft-NMS (ICCV 2017)
定位优先：IoU-Guided NMS (ECCV 2018)
加权平均：Weighted NMS (ICME Workshop 2017)
方差加权平均：Softer-NMS (CVPR 2019)
自适应阈值：Adaptive NMS (CVPR 2019)
+中心点距离：DIoU-NMS (AAAI 2020)

分类优先

传统NMS有多个名称，据不完全统计可以被称为：Traditional / Original / Standard / Greedy NMS，为统一起见，下称Traditional NMS。

Traditional NMS算法是最为经典的版本，伪代码如下：

算法流程解读：

给出一张图片和上面许多物体检测的候选框（即每个框可能都代表某种物体），但是这些框很可能有互相重叠的部分，我们要做的就是只保留最优的框。假设有N个框，每个框被分类器计算得到的分数为Si, 1<=i<=N。

0、建造一个存放待处理候选框的集合H，初始化为包含全部N个框；

建造一个存放最优框的集合M，初始化为空集。

1、将所有集合 H 中的框进行排序，选出分数最高的框 m，从集合 H 移到集合 M；

2、遍历集合 H 中的框，分别与框 m 计算交并比（Interection-over-union，IoU），如果高于某个阈值（一般为0~0.5），则认为此框与 m 重叠，将此框从集合 H 中去除。

3、回到第1步进行迭代，直到集合 H 为空。集合 M 中的框为我们所需。

需要优化的参数：

IoU 的阈值是一个可优化的参数，一般范围为0~0.5，可以使用交叉验证来选择最优的参数。

示例：

比如人脸识别的一个例子：

已经识别出了 5 个候选框，但是我们只需要最后保留两个人脸。

首先选出分数最大的框（0.98），然后遍历剩余框，计算 IoU，会发现露丝脸上的两个绿框都和 0.98 的框重叠率很大，都要去除。

然后只剩下杰克脸上两个框，选出最大框（0.81），然后遍历剩余框（只剩下0.67这一个了），发现0.67这个框与 0.81 的 IoU 也很大，去除。

至此所有框处理完毕，算法结果：

缺点：

顺序处理的模式，计算IoU拖累了运算效率。
剔除机制太严格，依据NMS阈值暴力剔除。
阈值是经验选取的。
评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

Soft-NMS是Traditional NMS的推广，主要旨在缓解Traditional NMS的第二条缺点。

数学上看，Traditional NMS的剔除机制可视为

$s_i=\left\{ \begin{array}{lc} 0, & IoU(M,B_i)\geqslant thresh\\ s_i, & IoU(M,B_i)si={0,si,IoU(M,Bi)⩾threshIoU(M,Bi)<thresh$

显然，对于IoU≥NMS阈值的相邻框，Traditional NMS的做法是将其得分暴力置0。这对于有遮挡的案例较不友好。因此Soft-NMS的做法是采取得分惩罚机制，使用一个与IoU正相关的惩罚函数对得分 s 进行惩罚。

线性惩罚：

$s_i=\left\{ \begin{array}{lc} s_i(1-IoU(M,B_i)), & IoU(M,B_i)\geqslant thresh\\ s_i, & IoU(M,B_i)si={si(1−IoU(M,Bi)),si,IoU(M,Bi)⩾threshIoU(M,Bi)<thresh$

其中 M 代表当前的最大得分框。

线性惩罚有不光滑的地方，因而还有一种高斯惩罚：

$s_i=s_ie^{-\frac{IoU(M,B_i)^2}{\sigma}}$

在迭代终止之后，Soft-NMS依据预先设定的得分阈值来保留幸存的检测框，通常设为0.0001

该文对两种惩罚方法的超参数也进行了实验，结果验证了超参数的不敏感性。经本人实测，Soft-NMS在Faster R-CNN中的提升约有0.5-0.8个点的AP提升。

缺点：

仍然是顺序处理的模式，运算效率比Traditional NMS更低。
对双阶段算法友好，而在一些单阶段算法上可能失效。
如果存在定位与得分不一致的情况，则可能导致定位好而得分低的框比定位差得分高的框惩罚更多(遮挡情况下)。
评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

定位优先

IoU-Guided NMS出现于IoU-Net一文中，研究者认为框的定位与分类得分可能出现不一致的情况，特别是框的边界有模棱两可的情形时。因而该文提出了IoU预测分支，来学习定位置信度，进而使用定位置信度来引导NMS。

具体来说，就是使用定位置信度作为NMS的筛选依据，每次迭代挑选出最大定位置信度的框 M ，然后将IoU≥NMS阈值的相邻框剔除，但把冗余框及其自身的最大分类得分直接赋予 M ，这样一来，最终输出的框必定是同时具有最大分类得分与最大定位置信度的框。

优点：

IoU-Guided NMS有助于提高严格指标下的精度，如AP75, AP90。

缺点：

顺序处理的模式，运算效率与Traditional NMS相同。
需要额外添加IoU预测分支，造成计算开销。
评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

加权平均

多框共同决定一框

Weighted NMS出现于ICME Workshop 2017《Inception Single Shot MultiBox Detector for object detection》一文中。论文认为Traditional NMS每次迭代所选出的最大得分框未必是精确定位的，冗余框也有可能是定位良好的。那么与直接剔除机制不同，Weighted NMS顾名思义是对坐标加权平均，加权平均的对象包括 M 自身以及IoU≥NMS阈值的相邻框。

M=\frac{\sum\limits_iw_iB_i}{\sum\limits_iw_i},\quad B_i\in{B|IoU(M,B)\geqslant thresh}\cup{M}

加权的权重为 w_i=s_iIoU(M,B_i) ，表示得分与IoU的乘积。

优点：

Weighted NMS通常能够获得更高的Precision和Recall，以本人的使用情况来看，只要NMS阈值选取得当，Weighted NMS均能稳定提高AP与AR，无论是AP50还是AP75，也不论所使用的检测模型是什么。

缺点：

顺序处理模式，且运算效率比Traditional NMS更低。
加权因子是IoU与得分，前者只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面；而后者受到定位与得分不一致问题的限制。

方差加权平均

Softer-NMS同样是坐标加权平均的思想，不同在于权重 w_i 发生变化，以及引入了box边界的不确定度。

关于目标检测box不确定度，可参考笔者的另一篇文章《一文了解目标检测边界框概率分布》

加权公式如下：

$M=\frac{\sum\limits_iw_iB_i/\sigma_i^2}{\sum\limits_iw_i/\sigma_i^2},\quad B_i\in\{B|IoU(M,B)\geqslant thresh\}\cup\{M\}$

其中权重 w_i=e^{{-\frac{(1-IoU(M,B_i))}2}{\sigma_t}} 抛弃了得分 s_i ，而只与IoU有关。

在加权平均的过程中，权重越大有两种情形：1. 与 M 的IoU越大；2. 方差越小，代表定位不确定度越低。

var voting表示方差加权平均

优点：

可以与Traditional NMS或Soft-NMS结合使用。
通常可以稳定提升AP与AR。

缺点：

顺序处理模式，且运算效率比Traditional NMS更低。
需要修改模型来预测方差。
加权因子是IoU与方差，前者依然只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

自适应阈值

以上这些NMS都基于这样的假设：与当前最高得分框重叠越大，越有可能是冗余框。

Adaptive NMS的研究者认为这在物体之间有严重遮挡时可能带来不好的结果。我们期望当物体分布稀疏时，NMS大可选用小阈值以剔除更多冗余框；而在物体分布密集时，NMS选用大阈值，以获得更高的召回。既然如此，该文提出了密度预测模块，来学习一个框的密度。

一个GT框 B_i 的密度标签定义如下，

d_i:=\max\limits_{B_i,B_j\in GT}IoU(B_i,B_j), \quad i\neq j

模型的输出将变为 (x,y,w,h,s,d) ，分别代表box坐标，宽高，分类得分，密度，其中密度 d 越大，代表该框所处的位置的物体分布越密集，越有可能是遮挡严重的地方；反之密度 d 越小，代表该框所处的位置的物体分布越稀疏，不太可能有遮挡。

论文以Traditionnal NMS和Soft-NMS的线性惩罚为基础，将每次迭代的NMS阈值更改如下：

$N_t=\max\{thresh, d_M\}$

其中 thresh 代表最小的NMS阈值。

优点：

可以与前面所述的各种NMS结合使用。
对遮挡案例更加友好。

缺点：

与Soft-NMS结合使用，效果可能倒退 (受低分检测框的影响)。
顺序处理模式，运算效率低。
需要额外添加密度预测模块，造成计算开销。
评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

+中心点距离

DIoU-NMS出现于Distance-IoU一文，研究者认为若相邻框的中心点越靠近当前最大得分框 M 的中心点，则其更有可能是冗余框。也就是说，考虑IoU相同的情况，如下所示

第一种相比于第三种越不太可能是冗余框。基于该观点，研究者使用所提出的DIoU替代IoU作为NMS的评判准则，公式如下：

$s_i=\left\{ \begin{array}{lc} 0, & DIoU(M,B_i)\geqslant thresh\\ s_i, & DIoU(M,B_i)si={0,si,DIoU(M,Bi)⩾threshDIoU(M,Bi)<thresh$

DIoU的定义为

$D I o U = I o U - d^{2} / c^{2}$

而在实际操作中，研究者还引入了参数 \beta ，用于控制 \frac{d^2}{c2} 的惩罚幅度。即

$DIoU=IoU-(\frac{d^2}{c^2})^\beta$

由公式可以看出，

当 $\beta\rightarrow\infty$ 时，DIoU退化为IoU，此时的DIoU-NMS与Traditional NMS效果相当。
当 $\beta\rightarrow0$ 时，此时几乎所有中心点不与 M 重合的框都被保留了。

研究者进一步比较了Traditional NMS和DIoU-NMS的性能，在YOLOv3和SSD上，选取NMS阈值为[0.43,0.48]。可以看到DIoU-NMS在每个阈值上都优于Traditional NMS，此外还值得一提的是，即便是性能最差的DIoU-NMS也比性能最好的Traditional NMS相当或更优，说明即便不仔细调整NMS阈值，DIoU-NMS也通常能够表现更好。

YOLOv3(左)和SSD(右)在VOC 2007 test集

这里顺便一提，既然都比了[0.43, 0.48]的阈值，就让人比较好奇更宽的阈值范围会怎样？Traditional NMS会不会有反超DIoU-NMS的情况？当然我个人比较认同DIoU-NMS更优的范围会大一些，也就是NMS阈值不必精调也可放心使用DIoU-NMS。

优点：

从几何直观的角度，将中心点考虑进来有助于缓解遮挡案例。
可以与前述NMS变体结合使用。
保持NMS阈值不变的情况下，必然能够获得更高recall (因为保留的框增多了)，至于precision就需要调 \beta 来平衡了。
个人认为+中心点距离的后处理可以与DIoU/CIoU损失结合使用，这两个损失一方面优化IoU，一方面指引中心点的学习，而中心点距离学得越好，应该对这种后处理思想的执行越有利。

缺点：

依然是顺序处理模式，运算效率低。
DIoU的计算比IoU更复杂一些，这会降低运算效率。
在保持NMS阈值不变的情况下，使用DIoU-NMS会导致每次迭代剩余更多的框，这会增加迭代轮数，进一步降低运算效率。(经本人实测，DIoU-NMS是Traditional NMS 起码1.5倍耗时)

总结：

加权平均法通常能够稳定获得精度与召回的提升。
定位优先法，方差加权平均法与自适应阈值法需要修改模型，不够灵活。
中心点距离法可作为额外惩罚因子与其他NMS变体结合。
得分惩罚法会改变box的得分，打破了模型校准机制。
运算效率的低下可能会限制它们的实时应用性。

效率提升

实际项目中，NMS往往能占模型计算总时间的40%甚至更多，极大影响了模型的效率。经过一段时间的调研，关于提升NMS运算速度的方法，在这里也将结合代码进行阶段性总结。

所参考的代码库列举如下：

Faster RCNN pytorch (rbg大神) 的 CUDA NMS https://github.com/rbgirshick/py-faster-rcnn
YOLACT团队提出的Fast NMS https://github.com/dbolya/yolact
CIoU团队提出的Cluster NMS https://github.com/Zzh-tju/CIoU
SOLOv2团队提出的Matrix NMS https://github.com/WXinlong/SOLO
Torchvision封装的免编译CUDA NMS

加速的关键

在进入正题之前，首先我们应该考察一下NMS运算效率的瓶颈在哪？答案自然是IoU计算及顺序迭代抑制。

假如一张图片中有 n 个检测框，由于顺序处理的原因，某一个框与其他框计算IoU，最少一次，最多有 n-1 次。再加上顺序迭代抑制，NMS算法在计算IoU方面，共需要计算IoU至少 n-1 次，最多 $(n-1)+(n-2)+\cdots+1=\frac{1}{2}n^2-\frac{n}{2}$ 次。

因此，要想加速NMS，首当其冲应该要将IoU的计算并行化。这个操作在我们使用IoU-based loss的时候就有，只需计算检测框集合 B={B_i}_{i=1,to,n} 与自身的IoU即可。检测框集合 B 事先会按照得分降序排列，也就是说 B_1 是最高得分框， B_n 是最低得分框。得到如下这个IoU矩阵：

$X=IoU(B,B)=\left(\begin{array}{cccc} x_{11}&x_{12}&\cdots&x_{1n}\\ x_{21}&x_{22}&\cdots&x_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n1}&x_{n2}&\cdots&x_{nn}\\ \end{array}\right),\quad x_{ij}=IoU(B_i, B_j)$

得益于GPU的并行计算，我们可以一次性得到IoU的全部计算结果。这一步就已经极大地解决了IoU计算繁琐又耗时的问题。代码如下：

def box_iou(boxes1, boxes2):
    # https://github.com/pytorch/vision/blob/master/torchvision/ops/boxes.py
    """
    Return intersection-over-union (Jaccard index) of boxes.
    Both sets of boxes are expected to be in (x1, y1, x2, y2) format.
    Arguments:
        boxes1 (Tensor[N, 4])
        boxes2 (Tensor[M, 4])
    Returns:
        iou (Tensor[N, M]): the NxM matrix containing the pairwise
            IoU values for every element in boxes1 and boxes2
    """

    def box_area(box):
        # box = 4xn
        return (box[2] - box[0]) * (box[3] - box[1])

    area1 = box_area(boxes1.t())
    area2 = box_area(boxes2.t())

    lt = torch.max(boxes1[:, None, :2], boxes2[:, :2])  # [N,M,2]
    rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:])  # [N,M,2]

    inter = (rb - lt).clamp(min=0).prod(2)  # [N,M]
    return inter / (area1[:, None] + area2 - inter)  # iou = inter / (area1 + area2 - inter)

到这里为止，以上列出的5种NMS都可以做到，从速度上来说CUDA NMS和torchvision NMS相对底层，编译后使用，速度稍快，但必然损失了一些灵活度，后面会讲。(关于CUDA NMS的教程，有兴趣的小伙伴可以参考faster-rcnn源码阅读：nms的CUDA编程，非常详实。

在有了IoU矩阵之后，接下来就是应该要如何利用它来抑制冗余框。

IoU矩阵的妙用

以下列举的三篇文献，可谓是将IoU矩阵玩出了花，从不同的角度发扬光大，在NMS加速方面也确实走在正轨上。(所用的一些符号，笔者进行了统一)

Fast NMS

Fast NMS是《YOLACT: Real-time Instance Segmentation》一文的其中一个创新点。由于IoU的对称性，即 IoU(B_i,B_j)=IoU(B_j,B_i) ，看出 X 是一个对称矩阵。再加上一个框自己与自己算IoU也是无意义的，因此Fast NMS首先对 X 使用pytorch的triu函数进行上三角化，得到了一个对角线元素及下三角元素都为0的IoU矩阵 X 。

$X=\left(\begin{array}{ccccc} 0&x_{12}&x_{13}&\cdots&x_{1n}\\ 0&0&x_{23}&\cdots&x_{2n}\\ 0&0&0&\cdots&x_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&0\\ \end{array}\right)$

接着对 X 执行按列取最大值操作，得到一维张量 $b=[b_1,b_2,\cdots,b_n]， b_i $代表了 X 的第 i 列上元素的最大值。最后使用NMS阈值，论文取0.5，对 b 二值化。 b 中元素小于NMS阈值的是保留的框，≥NMS阈值的是冗余框。例如

$\begin{array}{cccccc} &\;\;1\;\quad\;0\;\;\;\quad1\;\;\;\quad0\;\;\;\quad0\;\;\;\;\;\\ &\quad\quad\quad\quad\;\;\quad\quad\quad\quad\uparrow\;NMS阈值二值化\quad\\ b=&0\quad0.6\quad0.2\quad0.72\quad\,0.8\;\\ &\quad\quad\quad\quad\quad\uparrow\;列最大值\quad\\ X=&\left(\begin{array}{ccccc} 0&0.6&0.1&0.3&0.8\\ &0&0.2&0.72&0.1\\ &&0&0.45&0.12\\ &&&0&0.28\\ &&&&0\\ \end{array}\right)\end{array}$

1代表保留，0代表抑制。

代码如下：

def fast_nms(self, boxes, scores, NMS_threshold:float=0.5):
    '''
    Arguments:
        boxes (Tensor[N, 4])
        scores (Tensor[N, 1])
    Returns:
        Fast NMS results
    '''
    scores, idx = scores.sort(1, descending=True)
    boxes = boxes[idx]   # 对框按得分降序排列
    iou = box_iou(boxes, boxes)  # IoU矩阵
    iou.triu_(diagonal=1)  # 上三角化
    keep = iou.max(dim=0)[0] < NMS_threshold  # 列最大值向量，二值化

    return boxes[keep], scores[keep]

优点：

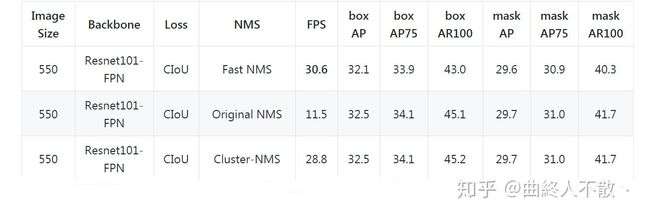
速度比cython编译加速的Traditional NMS快。(上表截自https://github.com/Zzh-tju/CIoU)
可支持与其他提升精度的NMS方法结合。

缺点：

Fast NMS会比Traditional NMS抑制更多的框，性能略微下降。
比CUDA NMS慢，约0.2ms。

这里有必要解释一下，为什么Fast NMS会抑制更多的框？

我们知道NMS的思想是：当一个框是冗余框，被抑制后，将不会对其他框产生任何影响。但在Fast NMS中，如果一个框 B_i 的得分比 B_j 高，且 B_i 被抑制了，矩阵 X 的第 i 行正是 B_i 与得分低于它的所有框的IoU，如果 x_{ij} 这个元素≥NMS阈值的话，那么在取列最大值这个操作时， b 的第 j 个元素必然≥NMS阈值，于是很不幸地 B_j 就被抑制掉了。

也就是在刚刚的例子中，由于第二个框 B_2 被抑制，那么第二行第四列的0.72就不应该存在，可是Fast NMS允许冗余框去抑制其他框，导致了第四个框 B_4 被错误地抑制了。

不过呢，YOLACT主要针对的是实例分割，mask是从box中裁剪出来的，Fast NMS对mask AP的下降比较轻微，约0.1~0.3的AP，但似乎对目标检测的box AP会下降更多。

Cluster NMS

Cluster NMS出自《Enhancing Geometric Factors in Model Learning and Inference for Object Detection and Instance Segmentation》一文。研究者主要旨在弥补Fast NMS的性能下降，期望也利用pytorch的GPU矩阵运算进行NMS，但同时又使得性能保持与Traditional NMS相同。

最开始看到这个名字时，笔者还以为是采取聚类的NMS，这不禁让人想起了今年2月的FeatureNMS。但后来仔细看了过后，发现这里的cluster的含义不一样。

以上是论文的原话，意思是说，cluster是一个框集合，若某一个框A属于这个cluster，则必有cluster中的框与A的IoU≥NMS阈值，且A不会与除这个cluster之外的框有IoU≥NMS阈值。举个简单的例子：

上图中的黑红蓝橙四个框构成一个cluster，而绿色的两个框构成一个cluster，虽然两个cluster之间有相交，但都没有超过NMS阈值，于是这两个框集合不能合并成一个cluster。

然后我们看一下Cluster NMS是怎么做的？

其实就是一个迭代式的Fast NMS。前面的过程与Fast NMS一模一样，都是 B 按得分降序排列，计算IoU矩阵，上三角化。然后按列取最大值，经过NMS阈值二值化得到一维张量 b 。但不同于Fast NMS直接输出了 b ，Cluster NMS而是利用 b ，将它展开成一个对角矩阵 E 。也就是这个对角矩阵 E 的对角线元素与 b 相同。然后用 E 去左乘IoU矩阵 X 。然后再按列取最大值，NMS阈值二值化得到一个新的一维张量 b，再展开成一个新的对角矩阵 E，继续左乘IoU矩阵 X 。直到出现某两次迭代后， b 保持不变了，那么谁该保留谁该抑制也就确定了。

这里借用一下作者在github的流程图。

以笔者的角度看，这种利用矩阵左乘的方式，其实就是在省略上一次Fast NMS迭代中被抑制的框对其他框的影响。

因为我们知道一个对角矩阵左乘一个矩阵，就是在做行变换啊，对应行是1，乘完的结果这一行保持不变，如果对应行是0，乘完的结果就是把这一行全部变成0。而 b 中某个元素若是0，就代表这个位置是冗余框，于是乘完之后，这个冗余框在下一次的迭代中就不再对其他框产生影响。为什么这里要强调下一次迭代？是因为这个迭代过程 b 会不断发生变动！可能某个框这会儿是冗余框，到了下一次迭代又变成了保留框。但是但是！到了最终 (其实未必是迭代满n次)， b 就保持不变了！你说奇怪不？这里论文还给出了一个命题，说Cluster NMS的输出结果与Traditional NMS的结果一模一样。

论文里还给出了对这个命题的证明，又是数学数学数学！大致一看是利用数学归纳法证的，感兴趣的可以去看论文，这里请允许我跳过。

def cluster_nms(self, boxes, scores, NMS_threshold:float=0.5):
    '''
    Arguments:
        boxes (Tensor[N, 4])
        scores (Tensor[N, 1])
    Returns:
        Fast NMS results
    '''
    scores, idx = scores.sort(1, descending=True)
    boxes = boxes[idx]   # 对框按得分降序排列
    iou = box_iou(boxes, boxes).triu_(diagonal=1)  # IoU矩阵，上三角化
    C = iou
    for i in range(200):    
        A=C
        maxA = A.max(dim=0)[0]   # 列最大值向量
        E = (maxA < NMS_threshold).float().unsqueeze(1).expand_as(A)   # 对角矩阵E的替代
        C = iou.mul(E)     # 按元素相乘
        if A.equal(C)==True:     # 终止条件
            break
    keep = maxA < NMS_threshold  # 列最大值向量，二值化

    return boxes[keep], scores[keep]

好了，至此Cluster NMS算是完成了对Fast NMS性能下降的弥补。我们直接看结果好了

嗯，效果还是可以的，保持了AP与AR一样，运算效率比Fast NMS下降了一些，毕竟是迭代Fast NMS的操作，但也比Traditional NMS快多了。

以为这样就完了？接下来才是重头戏！

这里又分为两个部分，一个是实用上的，另一个是理论上的。先说一下实用上的。

之前说过基于pytorch的NMS方法灵活度要比CUDA NMS更高，就在于这些基于pytorch的NMS是高层语言编写，专为研究人员开发，矩阵运算清晰简洁，于是乎可以很方便地与一些能够提升精度的NMS方法结合！正所谓强强联合，于是就诞生出了又快又好的一系列Cluster NMS的变体。

论文里主要举了三种变体：

得分惩罚机制SPM（Score Penalty Mechanism）

$s_j=s_j\prod\limits_ie^{-\frac{C_{ij}^2}{\sigma}}$

也就是对刚刚Cluster NMS终止后的矩阵 C=E\times X ，先做一个Soft-NMS里gaussian版的变换，然后将每一列上的元素连乘作为惩罚得分的系数。不过论文提到，虽然是叫得分惩罚机制，但又与Soft-NMS不同，因为这里的SPM不改变框的次序，再加上矩阵 C 是一个上三角矩阵的缘故，所以每个框都只会被得分高于它的框惩罚，并且这里已经排除了高得分的冗余框对它的惩罚。而Soft-NMS每次迭代惩罚得分后，需要重新按得分降序排列，所以框的次序会不断变动。

def SPM_cluster_nms(self, boxes, scores, NMS_threshold:float=0.5):
    '''
    Arguments:
        boxes (Tensor[N, 4])
        scores (Tensor[N, 1])
    Returns:
        Fast NMS results
    '''
    scores, idx = scores.sort(1, descending=True)
    boxes = boxes[idx]   # 对框按得分降序排列
    iou = box_iou(boxes, boxes).triu_(diagonal=1)  # IoU矩阵，上三角化
    C = iou
    for i in range(200):    
        A=C
        maxA = A.max(dim=0)[0]   # 列最大值向量
        E = (maxA < NMS_threshold).float().unsqueeze(1).expand_as(A)   # 对角矩阵E的替代
        C = iou.mul(E)     # 按元素相乘
        if A.equal(C)==True:     # 终止条件
            break
    scores = torch.prod(torch.exp(-C**2/0.2),0)*scores    #惩罚得分
    keep = scores > 0.01    #得分阈值筛选
    return boxes[keep], scores[keep]

+中心点距离

说到底DIoU就是该团队提出来的，那怎能不用上中心点距离呢？于是论文在两个方面添加了中心点距离。一个是IoU矩阵直接变成DIoU矩阵，由于DIoU也是满足尺度不变性的，所以完全没问题，相距很远的框之间的DIoU会变成负数，不过不影响过程。第二个是基于上面的SPM，公式如下：

$s_j=s_j\prod\limits_i\min\{e^{-\frac{C_{ij}^2}{\sigma}}+D^\beta,1\}$

这里多添了一个 D 也就是DIoU loss的惩罚项，两框中心点距离²/最小包围矩形对角线长度²。 \beta 用于控制中心点距离惩罚的幅度。然后又与1相比较，取最小值，以避免惩罚因子大于1。

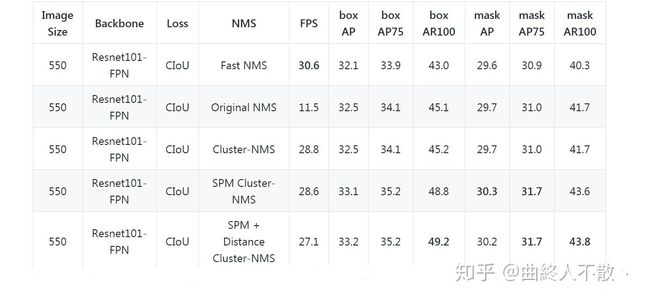
加了这两个变体之后，AP与AR得到了明显的改善，速度也是略微下降，很香

加权平均法Weighted NMS

也是利用矩阵 C ，先与得分张量 $S=[s_1,s_2,\cdots,s_n]$ 按列相乘得到 C’ ，随后

$B=C'\times B$

就可以更新框的坐标了。

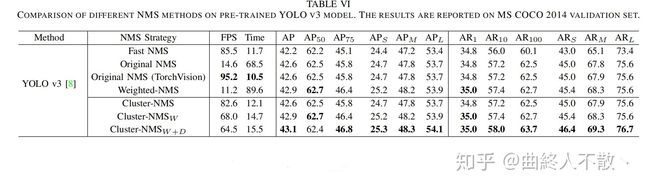
在YOLOv3上的效果有了不错的改进，虽然速度不及torchvision NMS，增加了5ms的运算成本，但结合Weighted NMS与DIoU，可以提升精度 (最后一行)。

def Weighted_cluster_nms(self, boxes, scores, NMS_threshold:float=0.5):
    '''
    Arguments:
        boxes (Tensor[N, 4])
        scores (Tensor[N, 1])
    Returns:
        Fast NMS results
    '''
    scores, idx = scores.sort(1, descending=True)
    boxes = boxes[idx]   # 对框按得分降序排列
    iou = box_iou(boxes, boxes).triu_(diagonal=1)  # IoU矩阵，上三角化
    C = iou
    for i in range(200):    
        A=C
        maxA = A.max(dim=0)[0]   # 列最大值向量
        E = (maxA < NMS_threshold).float().unsqueeze(1).expand_as(A)   # 对角矩阵E的替代
        C = iou.mul(E)     # 按元素相乘
        if A.equal(C)==True:     # 终止条件
            break
    keep = maxA < NMS_threshold  # 列最大值向量，二值化
    weights = (C*(C>NMS_threshold).float() + torch.eye(n).cuda()) * (scores.reshape((1,n)))
    xx1 = boxes[:,0].expand(n,n)
    yy1 = boxes[:,1].expand(n,n)
    xx2 = boxes[:,2].expand(n,n)
    yy2 = boxes[:,3].expand(n,n)

    weightsum=weights.sum(dim=1)         # 坐标加权平均
    xx1 = (xx1*weights).sum(dim=1)/(weightsum)
    yy1 = (yy1*weights).sum(dim=1)/(weightsum)
    xx2 = (xx2*weights).sum(dim=1)/(weightsum)
    yy2 = (yy2*weights).sum(dim=1)/(weightsum)
    boxes = torch.stack([xx1, yy1, xx2, yy2], 1)
    return boxes[keep], scores[keep]

接下来说一下Cluster NMS理论上的好处。

Cluster NMS的迭代次数通常少于Traditional NMS的迭代次数。

这一优点，从理论上给了它使用CUDA编程更进一步加速的可能。大致意思是说，平常我们在做NMS时，迭代都是顺序处理每一个cluster的。在Traditional NMS中，虽然不同的cluster之间本应毫无关系，但计算IoU重复计算了属于不同cluster之间的框，顺序迭代抑制的迭代次数也仍然保持不变。

但在Cluster NMS中，使用这种行变换的方式，就可以将本应在所有cluster上迭代，化简为只需在一个拥有框数量最多的cluster上迭代就够了(妙啊)。不同的cluster间享有相同的矩阵操作，且它们互不影响。这导致迭代次数最多不超过一张图中最大cluster所拥有的框的个数。也就是下面这种情形

上图中共有10个检测框，分成了3个cluster，它的IoU矩阵(被NMS阈值二值化了)在右边。Cluster NMS做迭代的次数最多不超过4次，因为上图中框数量最多的那个cluster(红色)一共只有4个框。而实际上这张图使用Cluster NMS，只需迭代2轮便结束了。

因此这带来的好处是时间复杂度的下降。特别是对于一张图中有很多个cluster时，效果更为显著。比如这种情形，密密麻麻的狗狗

物体数量越多，到时候的检测框也就越多，形成的cluster必然也会增多，于是乎Cluster NMS这种对所有cluster并行处理的算法必然迭代次数非常少，不会随着物体的增多而过分地增加迭代轮数。最极端的情形是 n 个物体形成 n 个cluster，Traditional NMS需要迭代 \geqslant n 次，而Cluster NMS不与cluster数量有关，只与需要迭代次数最多的那一个cluster有关。这也是为什么文中说，有可能可以被进一步使用工程技巧加速的原因，比如底层CUDA实现。

优点：

Cluster NMS可以保持与Traditional NMS一样的精度，速度快于Cython编译的Traditional NMS。
可以结合一些提升精度的方法，比如得分惩罚法，加权平均法，+中心点距离法。
并行处理cluster，给了算法迭代次数一个上界 (最大cluster的框数量)。

缺点：

速度上，各种变体Cluster NMS < Cluster NMS < Fast NMS < CUDA NMS

Matrix NMS

Matrix NMS出自《SOLOv2: Dynamic, Faster and Stronger》，也是利用排序过后的上三角化的IoU矩阵。不同在于它针对的是mask IoU。我们知道mask IoU的计算会比box IoU计算更耗时一些，特别是在Traditional NMS中，会加剧运算开销。因此Matrix NMS将mask IoU并行化是它最大的一个贡献。然后论文同样采取了得分惩罚机制来抑制冗余mask。具体代码如下：

不过笔者在实现这个代码时遇到了问题，惩罚因子decay通常会≥1，在考虑一个mask B_j 的惩罚因子decay时，与两个东西有关，一个是所有得分高于它的mask与Bj的IoU，该IoU越大，惩罚应该更多(也就是上图中decay的分子)；另一个是所有得分高于 B_j 的mask B_i 被抑制的概率(也就是上图中decay的分母)，这是由 B_i 所处的这一列的最大IoU决定，越大则 B_i 越可能是冗余mask，就应该降低对 B_j 的惩罚力度。

随后decay取列最小值。但依据如上代码，decay通常会≥1，这会增大mask的得分，而代码又以0.05作为score筛选的阈值，说明应该是减少得分的思想没有错，这个矛盾导致得出的结果奇差无比。如有任何人知道Matrix NMS出现这种问题的原因，还请告知我问题在哪。

这里直接贴出论文结果，从这里似乎也看出了相比于Soft-NMS每次迭代重排序的做法，直接得分惩罚也是可取的。

优点：

实现了mask IoU的并行计算，对于box-free的密集预测实例分割模型很有使用价值。
与Fast NMS一样，只需一次迭代。

缺点：

与Fast NMS一样，直接从上三角IoU矩阵出发，可能造成过多抑制。

总结：

CUDA NMS与Torchvision NMS稍快于以上三种基于pytorch实现的NMS，但比较死板，改动不易。
Cluster NMS基本可以取代Fast NMS，且与其他提升精度的方法的有机结合，使它又快又好。(目前作者团队的代码库只提供了得分惩罚法，+中心点距离，加权平均法三种。)
Matrix NMS也可以参考Cluster NMS的方式先得到一个与Traditional NMS一样的结果后，再进行后续处理。
三种基于pytorch的NMS方法，只依赖于矩阵操作，无需编译。
将2D检测的NMS加速方法推广至3D检测，应该也是很有价值的。

人知道Matrix NMS出现这种问题的原因，还请告知我问题在哪。