平衡二叉树(详细解释+完整C语言)
目录
1.前言
2.什么是平衡二叉树
2.1定义
2.2平衡因子
2.3结点结构
3.插入
3.1失衡
3.2旋转
3.3总结
3.4插入代码
4.删除
4.1删除叶子结点
4.2删除结点有左子树或右子树
4.3删除结点有左右子树
4.4删除代码
5.完整代码
6.运行结果
6.1LL
6.2RR
6.3LR
6.4RL
1.前言
在前面的学习过程中,我们了解到二叉排序树可以在一定程度上提高查找(搜索)的效率,但仍然会出现特殊情况,让二叉排序树失效。例如,将序列{1,2,3,4,5,6}中的元素依次插入到二叉排序树中,会得到右斜树,这就相当于一个单链表了,搜索效率降低为O(n)。
如若不清楚二叉排序树和单链表的,可以看下面两篇文章。
二叉排序树![]() https://blog.csdn.net/weixin_54186646/article/details/124412656?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_54186646/article/details/124412656?spm=1001.2014.3001.5501
单链表![]() https://blog.csdn.net/weixin_54186646/article/details/123312019?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_54186646/article/details/123312019?spm=1001.2014.3001.5501
那对于这种情况,我们有没有办法解决呢?于是,前辈们提出了另外一种二叉树类型——平衡二叉树(AVL树)。
2.什么是平衡二叉树
2.1定义
平衡⼆叉查找树:简称平衡⼆叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的一种高度平衡的⼆叉树,根据科学家的英文名也称为 AVL 树。
它具有以下两个性质:
- 可以是空树。
- 假如不是空树,任何⼀个结点的左子树与右子树都是平衡⼆叉树,并且高度之差的绝对值不超过 1。
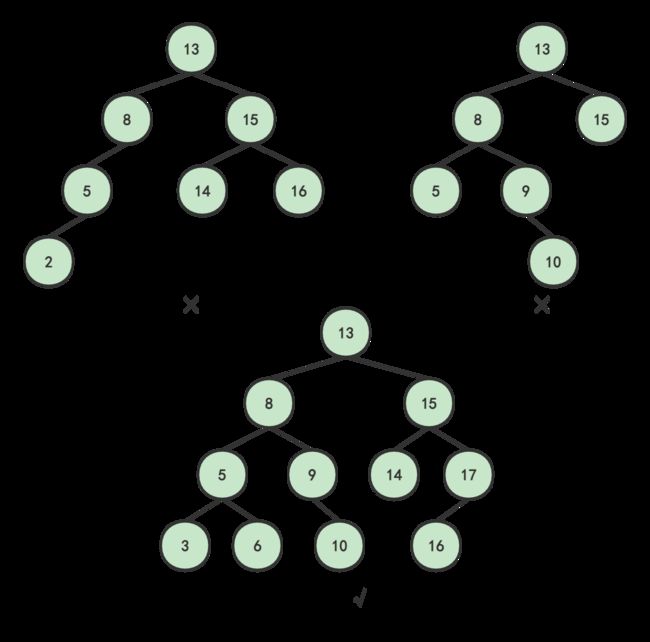
- 第一张图:8的左子树高度为2,右子树高度为0,失衡
- 第二张图:13的左子树高度为3,右子树高度为1,失衡
- 第三张图:每一个结点的左右子树高度差绝对值不超过1,平衡
于是,图1、图2不是平衡二叉树,图3是平衡二叉树。
另外,对于图1和图2:分别只有结点13、8失衡,其他结点都平衡。
2.2平衡因子
某结点的左子树与右子树的高度(深度)差即为该节点的平衡因子(BF,Balance Factor)。平衡⼆叉树中不存在平衡因子大于于 1 的节点。
在⼀棵平衡⼆叉树中,节点的平衡因子只能取0、1、-1
- 0 :左右子树等高
- 1:左子树比较高
- -1 :右子树比较高
2.3结点结构
typedef struct AVLNode
{
int data;
int height;
struct AVLNode* left;
struct AVLNode* right;
}Node;3.插入
3.1失衡
平衡二叉树的插入同二叉排序树,即:插入元素比当前结点更小,往左子树去找位置;插入元素比当前结点更大,往右子树去找位置。
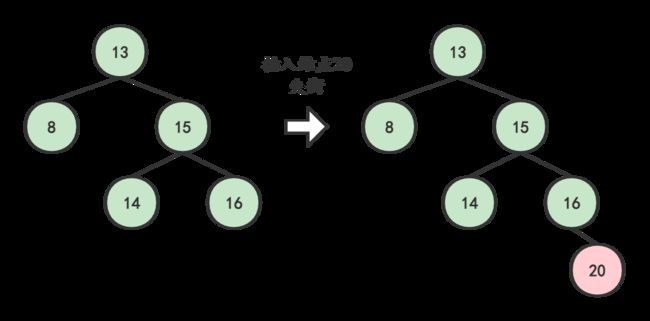
于是,我们在插入的过程中,就会使原本平衡的二叉树失衡,如图:
显然,上树在插入20后,13的左子树高度为1,右子树高度为3,显然失衡了。这时,我们就需要找到的一种办法,调整这棵树,使之重新平衡,而且这种方法应该是通用的。
3.2旋转
我们给出的方法是旋转这个树。怎么旋转呢?先别急,我们先介绍一个概念,以帮助我们更好的解释旋转。
最小失衡子树:在新插入的结点向上找,以第一个平衡因子绝对值大于1的结点为根的子树称为最小失衡子树。例如:上树中以父节点13的根的树为最小失衡子树。
显然,这时候13也是整课树的根结点,但往往更多的时候,失衡结点也不一定是全树的根结点,很可能只是某一部分子树失衡了,所以我们也只需要调整失衡的子树,其他部分不用调整。那么是怎么调整的呢?
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的,旋转分为左旋和右旋,其目的,就是减少树的高度(哪边高,就把那边向上旋转)。
3.2.1左旋—右孩子右子树
- 结点的右孩子替代此结点的位置
- 右孩子的左子树变成结点的右孩子
- 结点本身变成右孩子的左子树
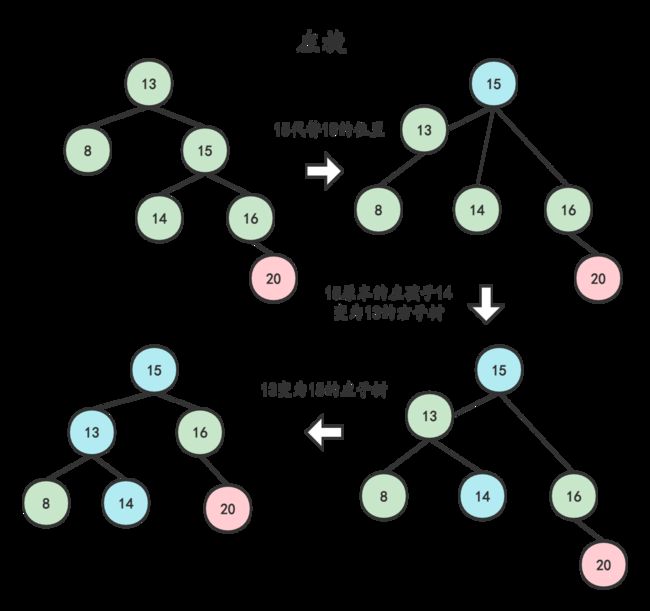
以下图为例,在插入结点20后。结点13发生了失衡,需要对13为父节点的子树进行旋转,由于插入的位置是在13右孩子的右子树上,所以我们通过左旋的方式来实现。
通过上述操作,我们把15向上旋转了,让原本的父节点13作为了15的左孩子,此时就变成了三叉树,需要将15原本的左子树接到13的右孩子处(这样,15也是二叉树,14的位置也是对的)
/*插入右孩子的右子树-左旋*/
//传入参数为最小失衡结点tree,对tree进行左旋
Node* right_right(Node* tree)
{
//结点调整
Node* k = tree->right;
tree->right = k->left;
k->left = tree;
//高度调整
k->height = MAX(get_height(k->left), get_height(k->right)) + 1;
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return k;
}代码实现分别结点调整与高度调整,
结点调整(旋转操作)
- 获取失衡结点tree的右孩子k;(k是旋转后的子树父节点)
- 将k的左子树给到了原父节点tree的右孩子
- 再将tree作为k的左孩子
高度调整(k与tree的高度发生了变化,其他的没变)
- 选择左子树与右子树更高的高度+1作为旋转后父节点k的高度
- 选择左子树与右子树更高的高度+1作为旋转后父节点tree的高度
3.2.2右旋-左孩子左子树
那如果是在左孩子的左子树插入结点导致失衡的呢?就采用与右旋相对应的左旋(右与左互换)。
- 结点的左孩子替代此结点的位置
- 左孩子的右子树变成结点的左孩子
- 结点本身变成左孩子的右子树
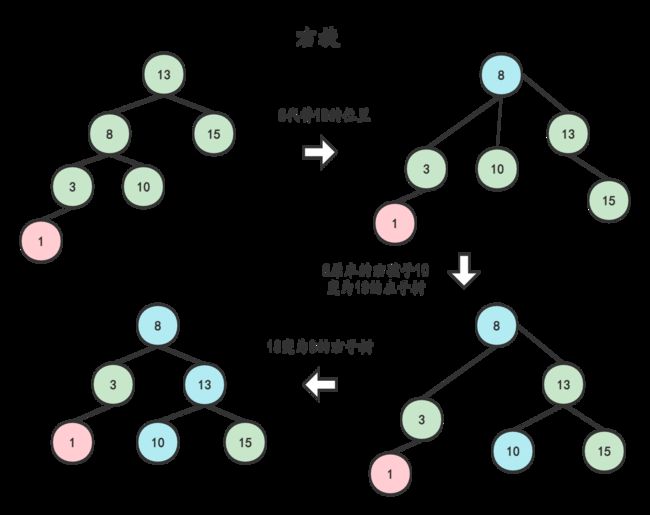
通过上述操作,我们把8向上旋转了,让原本的父节点13作为了8的右孩子,此时就变成了三叉树,需要将8原本的右子树接到13的右孩子处(这样,8也是二叉树,10的位置也是对的)
/*插入左孩子的左子树-右旋*/
//传入参数为最小失衡结点tree,对tree进行右旋
Node* left_left(Node* tree)
{
//结点调整
Node* k = tree->left;//保存tree的左孩子,k将是最终的父节点
tree->left = k->right;//将k的右孩子接到tree的左子树
k->right = tree;//tree作为k的右子树
//高度调整(这里指深度:用左右子树来判断)
k->height = MAX(get_height(k->left), get_height(k->right)) + 1;
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return k;
}3.2.3先右旋再左旋-左孩子右子树
这里我们解决了两种插入方式了,但还有两种,如果是在左孩子的右子树或者右孩子的左子树插入导致失衡呢?我们接着看。
左孩子的右子树,即在10的位置插入了元素9,导致13失衡,而插入结点9在13的左孩子8的右子树上。此时,我们先对13的左孩子8右旋,再对13左旋。其中,左右旋操作即3.2.1与3.2.2介绍的操作。
经旋转,此树又平衡了。
/*插入左孩子的右子树-先左旋再右旋*/
//对tree->left左旋(left_left),对tree右旋(right_right)
Node* left_right(Node* tree)
{
tree->left = right_right(tree->left);
tree = left_left(tree);
return tree;
}3.2.4先左旋再右旋-右孩子左子树
那如果是右孩子的左子树插入呢?我们依然采用相对应3.2.3的方式(左右互换)。
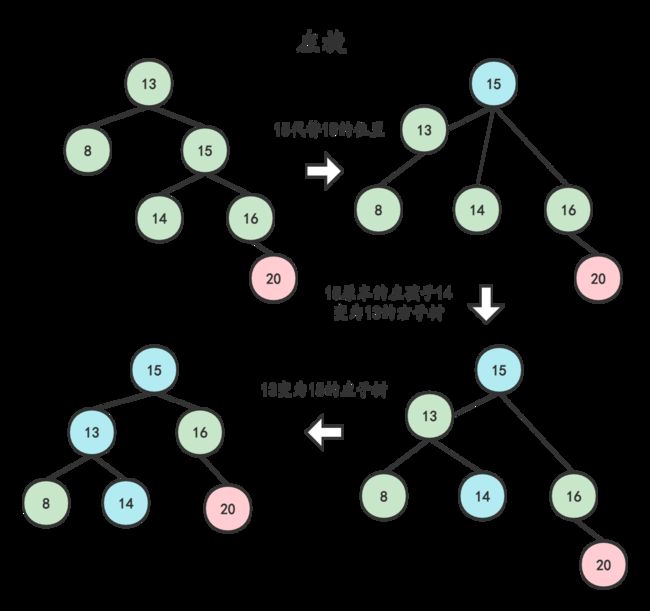
插入元素14,14按理应放在15后面,于是导致了13失衡。先对失衡结点13右孩子18左旋,再对13右旋。
/*插入右孩子的左子树-先右旋再左旋*/
//对tree->right右旋(left_left),对tree左旋
Node* right_left(Node* tree)
{
tree->right = left_left(tree->right);
tree = right_right(tree);
return tree;
}这样,我们就介绍完了所有的插入方式与失衡调整的方案,下面做一个总结。
3.3总结
根据以上四种插入方式,旋转方式总结如下:
| 插入方式 | 描述 | 旋转方式 |
|---|---|---|
| LL |
在结点A的左孩子的左子树插入导致A失衡 | 右旋 |
| RR | 在结点A的右孩子的右子树插入导致A失衡 | 左旋 |
| LR | 在结点A的左孩子的右子树插入导致A失衡 | 先左旋再右旋 |
| RL | 在结点A的右孩子的左子树插入导致A失衡 | 先右旋再左旋 |
注意:“先左旋”旋转的是失衡结点的左子树,“再右旋”旋转的是失衡结点。
3.4插入代码
结合旋转操作与二叉排序树插入操作的思想,我们给出代码。
/*往根节点为tree的树中插入一个值key*/
//插入位置同二叉排序树的逻辑,大于向右找位置,小于向左找位置
Node* Insert(Node* tree, int key)
{
//如果为空,就创建一棵树
if (tree == NULL)
{
Node* node = create(key);
tree = node;
}
//向左子树插入
else if (key < tree->data)
{
//递归寻找插入位置
tree->left = Insert(tree->left, key);
//判断是否失衡
if (get_height(tree->left) - get_height(tree->right) == 2)
{
//判断插入位置在左孩子的左子树还是右子树
if (key < tree->left->data)
tree = left_left(tree);
else
tree = left_right(tree);
}
}
//向右子树插入
else if (key > tree->data)
{
tree->right = Insert(tree->right, key);
if (get_height(tree->right) - get_height(tree->left) == 2)
{
if (key > tree->right->data)
tree = right_right(tree);
else
tree = right_left(tree);
}
}
else
printf("不允许插入重复的值\n");
//重新调整二叉树深度
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return tree;
}4.删除
在介绍完插入操作后,我们自然地应该来看看删除操作。删除的思想也同二叉排序树,但需要注意的是删除结点可能会导致树失衡,而且删除此结点,可能导致其他很多结点都失衡。也就是说:插入只需要修正第一个非平衡结点(1个),即可平衡;而删除需要修正所有的非平衡结点。
所以,它比插入操作更复杂,但没关系,我们继续分类讨论:
删除结点的类型:
- 删除叶子结点
- 删除结点只有左子树
- 删除结点只有右子树
- 删除结点有左、右子树
4.1删除叶子结点
- 将该节点直接从树中删除
- 其父结点的子树高度的变化将导致父节点平衡因子的变化,通过向上检索并推算其父节点是否失衡;
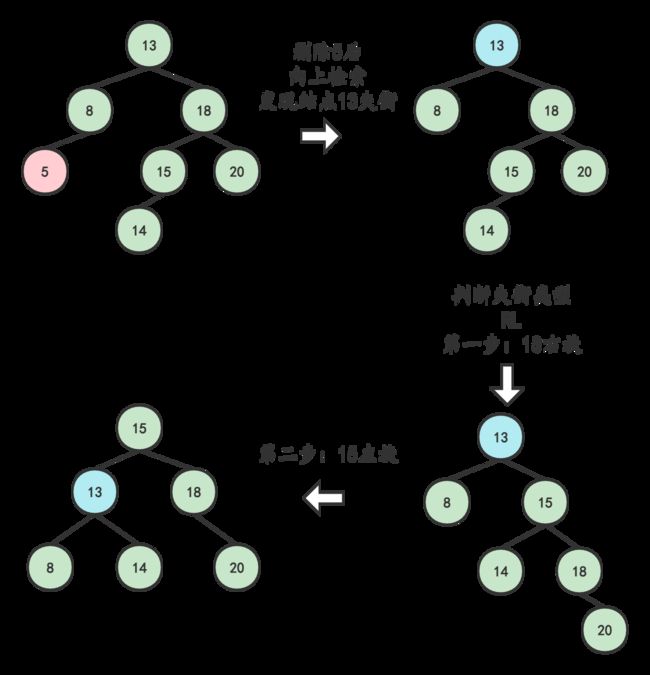
- 如果其父节点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复步骤2的判断,直到根结点 ;如果向上推算过程中发现了失衡的现象,则进行步骤 4;
- 如果其父结点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根结点的树的高度发生变化,则继续进行步骤2的检索推算; 如果与原来以父结点为根结点的高度⼀致时,则可说明父结点的父结点及祖先结点的平衡因子将不会有变化,因此可以退出处理
4.2删除结点有左子树或右子树
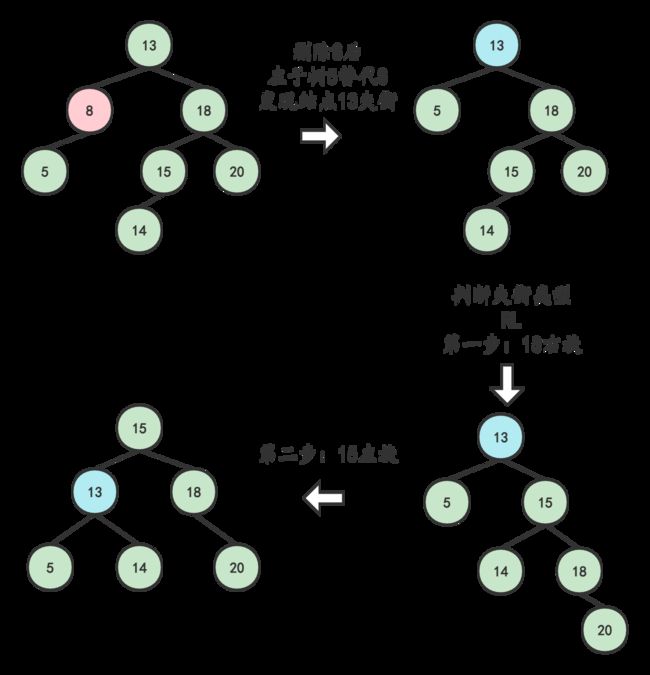
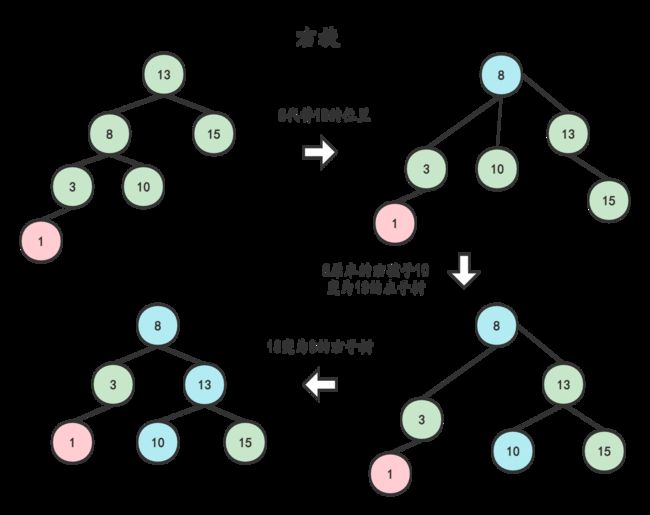
- 将左子树(右子树)替代原有结点8的位置
- 结点8被删除后,则以8的父结点13为起始推算点,依此向上检索推算各节点(父、祖先)是否失衡
- 如果其父结点未失衡,则继续向上检索推算其父节点的父结点是否失衡…如此反复步骤2的判断,直到根结点 ;如果向上推算过程中发现了失衡的现象,则进行步骤4的处理
- 如果其父结点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父结点为根结点的树的高度发生变化,则继续进行步骤2的检索推算; 如果与原来以父结点为根结点的高度⼀致时,则可说明父结点的父结点及祖先结点的平衡因子将不会有变化,因此可以退出处理
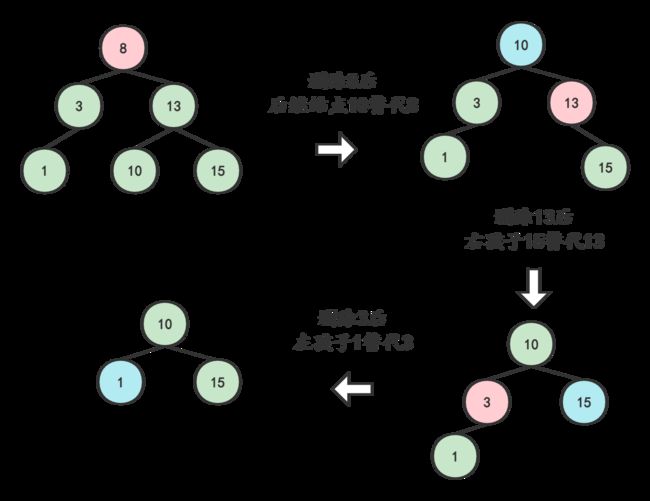
4.3删除结点有左右子树
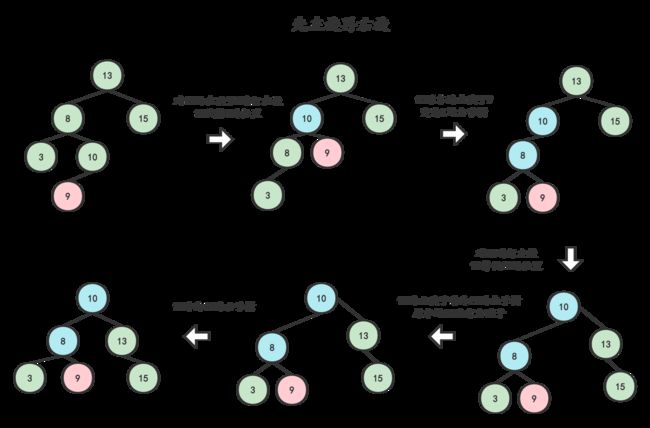
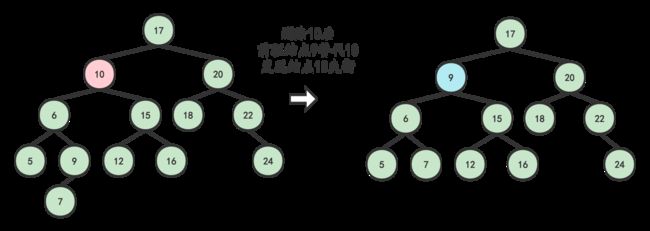
- 找到被删结点10和替代结点 9 (结点10 的前继结点或后继结点 ——此处选择前继)
- 将替代结点9 的值赋给结点 10 ,再把替代结点9的左孩子7替换替代结点9的位置
- 以9的父结点 6为起始推算点,依此向上检索推算父结点或祖先结点是否失衡
- 如果其父结点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复③的判断,直到根结点;如果向上推算过程中发现了失衡的现象,则进行⑤的处理
- 如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。 如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发⽣变化,则继续进行 ② 的检索推算;如果与原来以父结点为根结点的高度⼀致时,则可说明父节点的结节点及祖先结点的平衡因子将不会有变化,因此可以退出处理
4.4删除代码
/*删除结点*/
Node* del(Node* tree, int key)
{
//定位到要删除结点
Node* node = search(tree, key);
if (tree == NULL || node == NULL)
{
printf("删除失败\n");
return tree;
}
//若删除结点在左子树
if (key < tree->data)
{
//递归找到要删除结点
tree->left = del(tree->left, key);
//删除后要检查平衡
if (get_height(tree->right) - get_height(tree->left) == 2)
{
if (key < tree->right->data)
tree = right_left(tree);
else
tree = right_right(tree);
}
}
//若删除结点在右子树
else if (key > tree->data)
{
tree->right = del(tree->right, key);
if (get_height(tree->left) - get_height(tree->right) == 2)
{
if (key < tree->left->data)
tree = left_left(tree);
else
tree = left_right(tree);
}
}
//此时就是要删除结点,//待删除结点有左右孩子-同二叉排序树
else if (tree->left != NULL && tree->right != NULL)
{
Node* min_node = mininum(tree->right);
tree->data = min_node->data;
tree->right = del(tree->right, min_node->data);
}
//只有一个孩子或者没有孩子
else
tree = tree->left ? tree->left : tree->right;
if (tree)
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return tree;
}
5.完整代码
#include
#include
typedef struct AVLNode
{
int data;
int height;
struct AVLNode* left;
struct AVLNode* right;
}Node;
#define HEIGHT(node) ((node == NULL)? 0 : (((Node*)(node))->height ))
#define MAX(a,b) ((a > b) ? (a) : (b))
int get_height(Node* node)
{
return HEIGHT(node);
}
/*插入左孩子的左子树-右旋*/
//传入参数为最小失衡结点tree,对tree进行右旋
Node* left_left(Node* tree)
{
//结点调整
Node* k = tree->left;//保存tree的左孩子,k将是最终的父节点
tree->left = k->right;//将k的右孩子接到tree的左子树
k->right = tree;//tree作为k的右子树
//高度调整(这里指深度:用左右子树来判断)
k->height = MAX(get_height(k->left), get_height(k->right)) + 1;
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return k;
}
/*插入右孩子的右子树-左旋*/
//传入参数为最小失衡结点tree,对tree进行左旋
Node* right_right(Node* tree)
{
//结点调整
Node* k = tree->right;
tree->right = k->left;
k->left = tree;
//高度调整
k->height = MAX(get_height(k->left), get_height(k->right)) + 1;
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return k;
}
/*插入左孩子的右子树-先左旋再右旋*/
//对tree->left左旋(left_left),对tree右旋(right_right)
Node* left_right(Node* tree)
{
tree->left = right_right(tree->left);
tree = left_left(tree);
return tree;
}
/*插入右孩子的左子树-先右旋再左旋*/
//对tree->right右旋(left_left),对tree左旋
Node* right_left(Node* tree)
{
tree->right = left_left(tree->right);
tree = right_right(tree);
return tree;
}
/*创建一棵树,根结点为node*/
Node* create(int key)
{
Node* node = (Node*)malloc(sizeof(Node));
//此处可判断是否创建成功,我省略了
node->data = key;
node->left = NULL;
node->right = NULL;
node->height = 0;
return node;
}
/*往根节点为tree的树中插入一个值key*/
//插入位置同二叉排序树的逻辑,大于向右找位置,小于向左找位置
Node* Insert(Node* tree, int key)
{
//如果为空,就创建一棵树
if (tree == NULL)
{
Node* node = create(key);
tree = node;
}
//向左子树插入
else if (key < tree->data)
{
//递归寻找插入位置
tree->left = Insert(tree->left, key);
//判断是否失衡
if (get_height(tree->left) - get_height(tree->right) == 2)
{
//判断插入位置在左孩子的左子树还是右子树
if (key < tree->left->data)
tree = left_left(tree);
else
tree = left_right(tree);
}
}
//向右子树插入
else if (key > tree->data)
{
tree->right = Insert(tree->right, key);
if (get_height(tree->right) - get_height(tree->left) == 2)
{
if (key > tree->right->data)
tree = right_right(tree);
else
tree = right_left(tree);
}
}
else
printf("不允许插入重复的值\n");
//重新调整二叉树深度
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return tree;
}
/*查找结点*/
Node* search(Node* tree, int key)
{
if (tree == NULL || tree->data == key)
return tree;
else if (key < tree->data)
search(tree->left, key);
else
search(tree->right, key);
}
/*找到替换结点-左子树的最右边*/
Node* mininum(Node* tree)
{
if (tree == NULL)
return NULL;
while (tree->left)
tree = tree->left;
return tree;
}
/*删除结点*/
Node* del(Node* tree, int key)
{
//定位到要删除结点
Node* node = search(tree, key);
if (tree == NULL || node == NULL)
{
printf("删除失败\n");
return tree;
}
//若删除结点在左子树
if (key < tree->data)
{
//递归找到要删除结点
tree->left = del(tree->left, key);
//删除后要检查平衡
if (get_height(tree->right) - get_height(tree->left) == 2)
{
if (key < tree->right->data)
tree = right_left(tree);
else
tree = right_right(tree);
}
}
//若删除结点在右子树
else if (key > tree->data)
{
tree->right = del(tree->right, key);
if (get_height(tree->left) - get_height(tree->right) == 2)
{
if (key < tree->left->data)
tree = left_left(tree);
else
tree = left_right(tree);
}
}
//此时就是要删除结点,//待删除结点有左右孩子-同二叉排序树
else if (tree->left != NULL && tree->right != NULL)
{
Node* min_node = mininum(tree->right);
tree->data = min_node->data;
tree->right = del(tree->right, min_node->data);
}
//只有一个孩子或者没有孩子
else
tree = tree->left ? tree->left : tree->right;
if (tree)
tree->height = MAX(get_height(tree->left), get_height(tree->right)) + 1;
return tree;
}
/*前序遍历*/
void pre_order(Node* tree)
{
if (tree)
{
printf("%d ", tree->data);
pre_order(tree->left);
pre_order(tree->right);
}
}
/*中序遍历*/
void in_order(Node* tree)
{
if (tree)
{
in_order(tree->left);
printf("%d ", tree->data);
in_order(tree->right);
}
}
int main()
{
//第一种情况-左孩子的左子树
Node* tree1 = NULL;
int a1[] = { 13, 8, 15, 3, 10};
int l1 = sizeof(a1) / sizeof(int);
for (int i = 0; i < l1; i++)
{
tree1 = Insert(tree1, a1[i]);
}
printf("第一种情况-左孩子的左子树\n");
printf("前序遍历:");
pre_order(tree1);
printf("\n");
printf("中序遍历:");
in_order(tree1);
printf("\n");
printf("根结点的深度为:%d\n\n",tree1->height);
printf("插入1\n");
tree1 = Insert(tree1, 1);
printf("前序遍历:");
pre_order(tree1);
printf("\n");
printf("中序遍历:");
in_order(tree1);
printf("\n");
printf("根结点的深度为:%d\n\n", tree1->height);
printf("删除结点8\n");
tree1 = del(tree1, 8);
printf("前序遍历:");
pre_order(tree1);
printf("\n");
printf("中序遍历:");
in_order(tree1);
printf("\n");
printf("根结点的深度为:%d\n\n", tree1->height);
printf("删除结点13\n");
tree1 = del(tree1, 13);
printf("前序遍历:");
pre_order(tree1);
printf("\n");
printf("中序遍历:");
in_order(tree1);
printf("\n");
printf("根结点的深度为:%d\n\n", tree1->height);
printf("删除结点3\n");
tree1 = del(tree1, 3);
printf("前序遍历:");
pre_order(tree1);
printf("\n");
printf("中序遍历:");
in_order(tree1);
printf("\n");
printf("根结点的深度为:%d\n\n", tree1->height);
//第二种情况-右孩子的右子树
Node* tree2 = NULL;
int a2[] = { 13, 8, 15, 14, 16 };
int l2 = sizeof(a2) / sizeof(int);
for (int i = 0; i < l2; i++)
{
tree2 = Insert(tree2, a2[i]);
}
printf("第二种情况-右孩子的右子树\n");
printf("前序遍历:");
pre_order(tree2);
printf("\n");
printf("中序遍历:");
in_order(tree2);
printf("\n");
printf("根结点的深度为:%d\n\n", tree2->height);
tree2 = Insert(tree2, 20);
printf("插入20\n");
printf("前序遍历:");
pre_order(tree2);
printf("\n");
printf("中序遍历:");
in_order(tree2);
printf("\n");
printf("根结点的深度为:%d\n\n", tree2->height);
//第三种情况-左孩子的右子树
Node* tree3 = NULL;
int a3[] = { 13, 8, 15, 3, 10 };
int l3 = sizeof(a3) / sizeof(int);
for (int i = 0; i < l3; i++)
{
tree3 = Insert(tree3, a3[i]);
}
printf("第三种情况-左孩子的右子树\n");
printf("前序遍历:");
pre_order(tree3);
printf("\n");
printf("中序遍历:");
in_order(tree3);
printf("\n");
printf("根结点的深度为:%d\n\n", tree3->height);
tree3 = Insert(tree3, 9);
printf("插入9\n");
printf("前序遍历:");
pre_order(tree3);
printf("\n");
printf("中序遍历:");
in_order(tree3);
printf("\n");
printf("根结点的深度为:%d\n\n", tree3->height);
//第四种情况 - 右孩子的左子树
Node* tree4 = NULL;
int a4[] = { 13, 8, 18, 15, 20 };
int l4 = sizeof(a4) / sizeof(int);
for (int i = 0; i < l4; i++)
{
tree4 = Insert(tree4, a4[i]);
}
printf("第四种情况-右孩子的左子树\n");
printf("前序遍历:");
pre_order(tree4);
printf("\n");
printf("中序遍历:");
in_order(tree4);
printf("\n");
printf("根结点的深度为:%d\n\n", tree4->height);
tree4 = Insert(tree4, 14);
printf("插入14\n");
printf("前序遍历:");
pre_order(tree4);
printf("\n");
printf("中序遍历:");
in_order(tree4);
printf("\n");
printf("根结点的深度为:%d\n\n", tree4->height);
} 6.运行结果
6.1LL
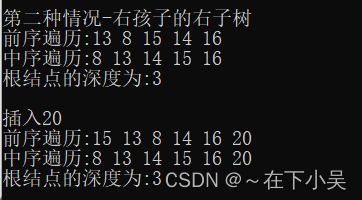
6.2RR
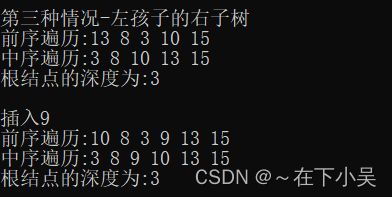
6.3LR
6.4RL
恭喜你呀,到此为止,除了高级搜索树外, 树的内容就介绍完了,下一节开始图的部分咯!