图灵机

一、图灵机的起源——可计算性理论

在20世纪以前，人们普遍认为，所有的问题类都是有算法的，人们的计算研究就是找出算法来。1900年，当时著名的大数学家希尔伯特在世纪之交的数学家大会上给国际数学界提出了著名的23个数学问题。
其中第十问题是这样的：

存在不存在一种有限的、机械的步骤能够判断“丢番图方程”是否存在解？

“丢番图方程”指：有一个或者几个变量的整系数方程，它们的求解仅仅在整数范围内进行。
上面这个问题简单点解释是：随便给一个不确定的方程，是否通过有限的步骤运算，判断这个方程是否存在整数解。

这个问题在1970年，苏联一个数学家证明了其实很多数学问题，是没有答案，甚至没有答案的问题比有答案的问题还要多。

这里就提出来了有限的、机械的证明步骤的问题，其实就是算法。但在当时，人们还不知道“算法”是什么。实际上，当时数学领域中已经有很多问题都是跟“算法”密切相关的，因而，科学的 “算法” 定义呼之欲出。之后到了30年代的时候，终于有两个人分别提出了精确定义算法的方法，一个人是图灵，一个人是丘奇。而其中图灵提出来的图灵机模型直观形象。

图灵思考这个问题的方式和常人不一样，在写前面提到的论文《论可计算数及其在判定性问题上的应用》的时候，图灵在思考三个问题

1. 世界上是否所有的数学问题都有明确的答案？
2. 如果有明确的答案，是否可以通过有限步骤的计算得到答案？
3. 对于那些有可能在有限步骤计算出来的学习问题，是否有一种假想的机械，让它不断运行，最后机器停下来的时候，那个数学答案就计算出来了？

图灵这样的天才考虑问题的认知是高屋建瓴的。
图灵首先考虑的是是否所有数学问题都用解，如果这个问题不解决，辛辛苦苦解题，最后发现无解，一切的努力都是浪费时间和精力。

对于存在答案的数学问题，只有部分是可以在有限步骤内完成，这样把计算机的边界确定下来了。

确定了边界之后，就要设计一种通用、有效、等价的机器，保证可以按照这个方法做事，最后得到答案。而图灵机就是图灵设计出来的这样的一个机器，严格来讲是一种数学模型、计算理论模型。

从图灵机提出到现在已经过去了80多年，今天所有的计算机，包括量子计算机都没有超出图灵机的理论范畴。

二、什么是图灵机

图灵机，又称图灵计算、图灵计算机，是由数学家艾伦·麦席森·图灵（1912～1954）提出的一种抽象计算模型，即将人们使用纸笔进行数学运算的过程进行抽象，由一个虚拟的机器替代人们进行数学运算。

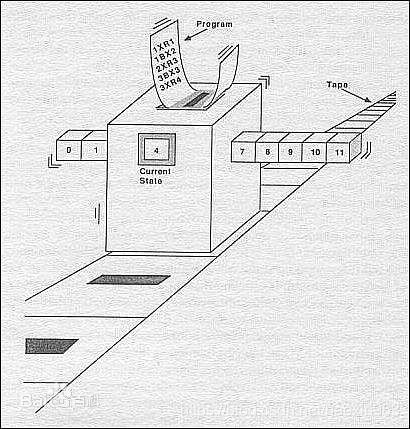
图灵机指一个抽象的机器，它有一条无限长的纸带，纸带分成了一个一个的小方格，每个方格有不同的颜色。有一个机器头在纸带上移来移去。机器头有一组内部状态，还有一些固定的程序。在每个时刻，机器头都要从当前纸带上读入一个方格信息，然后结合自己的内部状态查找程序表，根据程序输出信息到纸带方格上，并转换自己的内部状态，然后进行移动。

每一个会决策、会思考的人都可以被抽象地看成一台图灵机。该模型主要有四要素：输入集合、输出集合、内部状态和固定的程序。如果把人进行抽象，那么输入集合就是所处环境中所看到、听到、闻到、感觉到的一切；输出集合就是人的每一言每一行，还有表情动作；内部状态集合则可以把神经细胞的状态组合看成一个内部状态，所有可能的状态集合将是天文数字。

人有记忆，图灵机有没有？有，它有了内部状态就可以看成有记忆，内部状态会记录所经历过的世界。

很多现象似乎都能被图灵机包括，如人了IDE情绪和情感，可以看成某种内部状态，心情好的情绪下，输入和输出是一套规则，而心情不好的情况下，输入输出又是另外一种规则。

无论是神经元传递信息、变化状态的规律都是固定的，可以被程序化。那么头脑作为神经元的整体，它的运作也比如遵循固定的规则，即程序。正如图灵相信的，人脑也不会超越图灵机模型。

关于图灵机的学习问题，看似图灵机不包括学习，因为学习就意味着程序的改变，而图灵机不能在运行过程中改变自己的程序。很有可能一个图灵机的规则没有改变，只不过激活了它的某些内部状态，因为发生了本质的变化，尽管给它相同的输入，它却有完全不同的输出，这样看起来似乎它会学习了，虽然图灵机的程序一点都没变。

三、图灵机的意义

1、它证明了通用计算理论，肯定了计算机实现的可能性，同时它给出了计算机应有的主要架构；

库尔特·哥德尔在他的论文On Formally Undecidable Propositions of Principia Mathematica and Related Systems中提到了不完备性理论，解决了“希尔伯特判定性问题”中的完备性和一致性的不共存关系之后，这个问题便只剩下了决定性没有得到证明。于是这个问题便留到了五年后，在一篇名为On Computable Numbers, with an Application to the Entscheidungsproblem的论文中得到了最终的解答。这就是图灵享誉世界很重要的一篇论文。用类似有限状态机的原理（注意仅是类似，因为图灵机的功能远超过了有限状态机）定义了“有限次运算”，并用图灵机运算过程定义了“可行的过程”并将之重新命名为“算法”（algorithm）。这便是如今计算机体系结构以及程序算法设计最开始萌芽的地方。

2、图灵机模型引入了读写与算法与程序语言的概念，极大的突破了过去的计算机器的设计理念；

算法是一个古老的数学概念，算法事实上是解题的系统步骤。艾伦・图灵在1936年提出的“图灵机”概念,是一般算法的典型代表。其目的是为了解决“希尔伯特第十问题”———数学问题的一般算法步骤问题,也就是在原则上是否存在一般数学问题的解题步骤的判决问题。希尔伯特的规划是要把数学置于无懈可击的牢固的基础上,其中的公理和步骤法则一旦确立就不再改变。他想一劳永逸地解决数学的可靠性问题。

3、图灵机模型理论是计算学科最核心的理论，因为计算机的极限计算能力就是通用图灵机的计算能力，很多问题可以转化到图灵机这个简单的模型来考虑。

通用图灵机等于向我们展示这样一个过程：程序和其输入可以先保存到存储带上，图灵机就按程序一步一步运行直到给出结果，结果也保存在存储带上。另外，我们也可以看到现代计算机主要构成（冯.诺依曼结构），存储器，中央处理器，IO系统。

4、“图灵机”只是假象的“计算机”，完全没有考虑硬件状态，考虑的焦点是逻辑结构。

图灵在他著作里，进一步设计出被人们称为“通用图灵机”的模型，图灵机可以模拟其他任何一台解决某个特定数学问题的“图灵机”的工作状态。图灵甚至还想象在带子上存储数据和程序。“通用图灵机”实际上就是现代通用计算机的最原始的模型。