CSDN每日一题学习训练——Python版(N皇后 II、买卖股票的最佳时机 II、编程通过键盘输入每一位运动员)
版本说明
当前版本号[20231120]。
| 版本 | 修改说明 |
|---|---|
| 20231120 | 初版 |
目录
文章目录
- 版本说明
- 目录
- N皇后 II
-
- 题目
- 解题思路
- 代码思路
- 参考代码
- 买卖股票的最佳时机 II
-
- 题目
- 解题思路
- 代码思路
- 参考代码
- 编程通过键盘输入每一位运动员
-
- 题目
- 解题思路
- 代码思路
- 参考代码
N皇后 II
题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
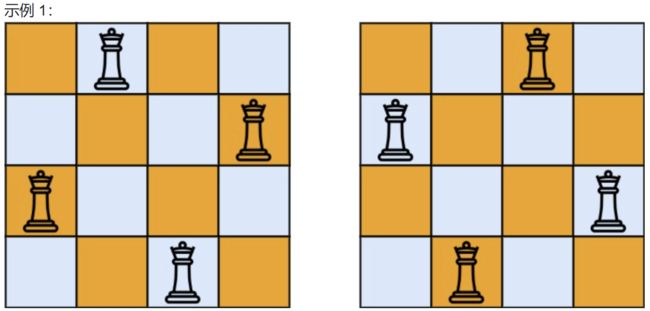
示例 1:
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
以下程序实现了这一功能,请你填补空白处内容:
class Solution(object):
def __init__(self):
self.count = 0
def totalNQueens(self, n):
self.dfs(0, n, 0, 0, 0)
return self.count
def dfs(self, row, n, column, diag, antiDiag):
if row == n:
self.count += 1
return
for index in range(n):
isColSafe = (1 << index) & column == 0
isDigSafe = (1 << (n - 1 + row - index)) & diag == 0
isAntiDiagSafe = (1 << (row + index)) & antiDiag == 0
if isAntiDiagSafe and isColSafe and isDigSafe:
_________________________;
if __name__ == '__main__':
s = Solution()
print (s.totalNQueens(4))
解题思路
- 初始化一个计数器 count,用于记录解决方案的数量。
- 定义一个深度优先搜索函数 dfs,用于寻找 n 皇后问题的解决方案。
- 在 dfs 函数中,使用递归的方式进行深度优先搜索。
- 对于每一行,遍历每一列,检查当前位置是否安全(即没有其他皇后在同一行、同一列或同一对角线上)。
- 如果当前位置安全,继续搜索下一行,并更新 column、diag 和 antiDiag 的值。
- 如果已经放置了 n 个皇后,找到一个解决方案,增加计数器 count 的值。
- 返回计数器 count 的值作为解决方案数量。
代码思路
-
定义一个名为Solution的类,包含一个初始化方法__init__和一个计算解决方案数量的方法totalNQueens。
-
在初始化方法中,将计数器count初始化为0。
class Solution(object): def __init__(self): self.count = 0 # 初始化计数器为0 -
在totalNQueens方法中,调用深度优先搜索函数dfs,传入初始参数row=0, n=棋盘大小, column=0, diag=0, antiDiag=0。
def totalNQueens(self, n): """ 计算n皇后问题的解决方案数量 :param n: 棋盘大小 :return: 解决方案数量 """ self.dfs(0, n, 0, 0, 0) # 从第0行开始深度优先搜索 return self.count # 返回解决方案数量 -
在dfs函数中,使用递归的方式进行深度优先搜索。
def dfs(self, row, n, column, diag, antiDiag): """ 深度优先搜索函数,用于寻找n皇后问题的解决方案 :param row: 当前行数 :param n: 棋盘大小 :param column: 列掩码,表示已经放置的皇后所在的列 :param diag: 主对角线掩码,表示已经放置的皇后所在的主对角线 :param antiDiag: 副对角线掩码,表示已经放置的皇后所在的副对角线 """ -
如果已经放置了n个皇后,找到一个解决方案,增加计数器self.count的值。
if row == n: # 如果已经放置了n个皇后,找到一个解决方案 self.count += 1 # 增加解决方案计数器 return -
遍历每一列,检查当前位置是否安全(即没有其他皇后在同一行、同一列或同一对角线上)。
for index in range(n): # 遍历每一列 -
如果当前位置安全,继续搜索下一行,更新column、diag和antiDiag的值。
-
最后,返回计数器self.count的值作为解决方案的数量。
isColSafe = (1 << index) & column == 0 # 检查当前列是否安全 isDigSafe = (1 << (n - 1 + row - index)) & diag == 0 # 检查主对角线是否安全 isAntiDiagSafe = (1 << (row + index)) & antiDiag == 0 # 检查副对角线是否安全 if isAntiDiagSafe and isColSafe and isDigSafe: # 如果当前位置安全,继续搜索下一行 self.dfs(row + 1, n, (1 << index) | column, (1 << (n - 1 + row - index)) | diag, (1 << (row + index)) | antiDiag) -
在主程序中,创建一个Solution对象s,并调用totalNQueens方法,传入棋盘大小n=4,输出4皇后问题的解决方案数量。
if __name__ == '__main__':
s = Solution() # 创建Solution对象
print(s.totalNQueens(4)) # 输出4皇后问题的解决方案数量
参考代码
这段代码是使用深度优先搜索算法来寻找所有可能的解决方案,并返回解决方案的数量。
self.dfs(row + 1, n, (1 << index) | column,
(1 << (n - 1 + row - index)) | diag,
(1 << (row + index)) | antiDiag)
买卖股票的最佳时机 II
题目
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
解题思路
- 初始化两个变量,hold表示持有股票的标志,0表示不持有,1表示持有;pric用于记录买入和卖出的价格;temp用于记录每次交易的利润;flag表示买入价格的索引;msum表示最大利润。
- 如果价格列表长度小于等于2,直接计算最大利润。如果价格列表为空,返回0;如果只有一个价格,返回0;如果第一个价格大于第二个价格,返回0;如果第一个价格小于第二个价格,返回第二个价格减去第一个价格。
- 遍历价格列表,找到买入和卖出的价格。如果下一个价格大于当前价格且不持有股票,将持有标志设为1,记录买入价格的索引,继续遍历;如果下一个价格小于当前价格且持有股票,将买入和卖出的价格分别添加到pric列表中,将持有标志设为0,继续遍历;否则,继续遍历。
- 计算每次交易的利润,并更新最大利润。遍历pric列表,每次取相邻的两个元素作为买入和卖出价格,计算利润,并将利润添加到temp列表中。然后更新最大利润msum为temp列表中所有元素的和。
- 如果最后还持有股票,将最后一天的价格加入最大利润。计算最后一天与买入价格之间的差值,加到最大利润msum上。
- 返回最大利润msum。
代码思路
-
定义一个类
Solution,包含一个方法maxProfit,接收一个参数prices,表示股票价格的列表。 -
初始化变量
hold为0,表示持有股票的标志;pric为空列表,用于记录买入和卖出的价格;temp为空列表,用于记录每次交易的利润;flag为0,表示买入价格的索引;msum为0,表示最大利润。hold = 0 # 持有股票的标志,0表示不持有,1表示持有 pric = [] # 记录买入和卖出的价格 temp = [] # 记录每次交易的利润 flag = 0 # 记录买入价格的索引 msum = 0 # 记录最大利润 -
如果价格列表长度小于等于2,直接计算最大利润。如果价格列表为空,返回0;如果只有一个价格,返回0;如果第一个价格大于第二个价格,返回0;如果第一个价格小于第二个价格,返回第二个价格减去第一个价格。
# 如果价格列表长度小于等于2,直接计算最大利润 if len(prices) <= 2: if not prices: return 0 if len(prices) == 1: return 0 if prices[0] > prices[1]: return 0 if prices[0] < prices[1]: return prices[1] - prices[0] -
遍历价格列表,找到买入和卖出的价格。如果下一个价格大于当前价格且不持有股票,将持有标志设为1,记录买入价格的索引;如果下一个价格小于当前价格且持有股票,将买入和卖出的价格分别添加到
pric列表中,并将持有标志设为0。# 遍历价格列表,找到买入和卖出的价格 for i in range(len(prices) - 1): if prices[i + 1] > prices[i] and hold != 1: hold = 1 flag = i continue if prices[i + 1] < prices[i] and hold == 1: pric.append(prices[flag]) pric.append(prices[i]) hold = 0 else: continue -
计算每次交易的利润,将每次交易的利润添加到
temp列表中,并更新最大利润。# 计算每次交易的利润,并更新最大利润 for i in range(0, len(pric), 2): temp.append(pric[i + 1] - pric[i]) msum = sum(temp) -
如果最后还持有股票,将最后一天的价格加入最大利润。
# 如果最后还持有股票,将最后一天的价格加入最大利润 if hold == 1: msum = msum + prices[-1] - prices[flag] -
返回最大利润。
参考代码
这段代码是一个股票交易问题的解法,通过遍历价格列表来找到买入和卖出的价格,并计算每次交易的利润。
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
hold = 0
pric = []
temp = []
flag = 0
msum = 0
if len(prices) <= 2:
if not prices:
return 0
if len(prices) == 1:
return 0
if prices[0] > prices[1]:
return 0
if prices[0] < prices[1]:
return prices[1] - prices[0]
for i in range(len(prices) - 1):
if prices[i + 1] > prices[i] and hold != 1:
hold = 1
flag = i
continue
if prices[i + 1] < prices[i] and hold == 1:
pric.append(prices[flag])
pric.append(prices[i])
hold = 0
else:
continue
for i in range(0, len(pric), 2):
temp.append(pric[i + 1] - pric[i])
msum = sum(temp)
if hold == 1:
msum = msum + prices[-1] - prices[flag]
return msum
编程通过键盘输入每一位运动员
题目
体操比赛成绩统计。多名运动员,多个评委打分,去掉一个最高分和去掉一个最低分,对其余分数求平均分作为一个运动员成绩。 编程通过键盘输入每位运动员编号和每个评委的成绩,求出运动员的最终成绩,并将运动员编号和最终成绩保存在一个字典中,形如{编号1:最终成绩1,学号2:最终成绩2…,并将结果输出。
解题思路
- 首先,我们需要获取评委人数和学生人数,确保评委人数不少于3人,学生人数不少于1人。
- 然后,我们需要初始化一个空的学生列表,用于存储每个学生的相关信息。
- 接下来,我们需要遍历学生人数,对于每个学生,我们需要初始化一个包含评分列表、学号、最低分、最高分和平均分的字典。
- 在每个学生字典中,我们需要输入学生的学号,并遍历评委人数,获取每个评委的评分,并将其添加到评分列表中。
- 对评分列表进行排序,然后去掉最低分和最高分,计算剩余分数的平均分,并将结果更新到学生字典中。
- 将学生字典添加到学生列表中。
- 使用字典推导式生成学生学号和最终成绩的字典。
- 最后,输出结果。
代码思路
-
首先,通过输入获取评委人数和学生人数。
-
然后,初始化一个空的学生列表。
# 输入评委人数,不得少于3人 t = int(input('请输入评委人数(不得少于3人):')) # 输入学生人数,不得少于1人 s = int(input('请输入学生人数(不得少于1人):')) # 初始化学生列表 stus = [] -
接着,遍历学生人数,对于每个学生,初始化一个包含评分列表、学号、最低分、最高分和平均分的字典。
# 遍历学生人数 for i in range(s): # 初始化学生字典,包含评分列表、学号、最低分、最高分和平均分 stu = {'score':[]} -
在每个学生字典中,通过输入获取学生的学号,并遍历评委人数,获取每个评委的评分,并将其添加到评分列表中。
# 输入学生学号 stu.update({'sn':str(input('----\n请输入学生学号:'))}) # 遍历评委人数 for j in range(t): # 输入评委的评分 stu['score'].append(input('请输入评委'+str(j+1)+'的评分:')) -
对评分列表进行排序,然后获取最低分和最高分,并计算平均分。
# 对评分列表进行排序 stu['score'].sort() # 获取最低分 stu.update({'min':stu['score'].pop(0)}) # 获取最高分 stu.update({'max':stu['score'].pop()}) # 计算平均分并更新字典 stu.update({'avg':sum(stu['score'])/len(stu['score'])}) -
将学生字典添加到学生列表中。
# 将学生字典添加到学生列表中 stus.append(stu) -
最后,使用字典推导式生成学生学号和平均分的字典,并输出结果。
# 使用字典推导式生成学生学号和平均分的字典
r = {n['sn']:n['avg'] for n in stus}
参考代码
t = int(input('请输入评委人数(不得少于3人):'))
s = int(input('请输入学生人数(不得少于1人):'))
stus = []
for i in range(s):
stu = {'score':[]}
stu.update({'sn':str(input('----\n请输入学生学号:'))})
for j in range(t):
stu['score'].append(input('请输入评委'+str(j+1)+'的评分:'))
stu['score'].sort()
stu.update({'min':stu['score'].pop(0)})
stu.update({'max':stu['score'].pop()})
stu.update({'avg':eval('+'.join(stu['score']))/len(stu['score'])})
stus.append(stu)
r = {n['sn']:n['avg'] for n in stus}
print(r)