数学建模值TOPSIS法及代码

TOPSIS法

TOPSIS法简称为优劣距离解法，是一种常见法综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各个评价方案之间的差距。

模型介绍

上篇文章谈到的层次分析法是有局限性的。比如评价的决策层不能太多，太多的话n会很大，判断矩阵和一致性矩阵差异可能会很大。其次，其无法利用原始的数据来做精确的评价。这个时候就体现出TOPSIS法的好处了。

它在原始数据上，充分反映各个评价方案之间的差距。

统一指标类型

将所有的指标转换为极大型称为指标正向化。（最常用）

---

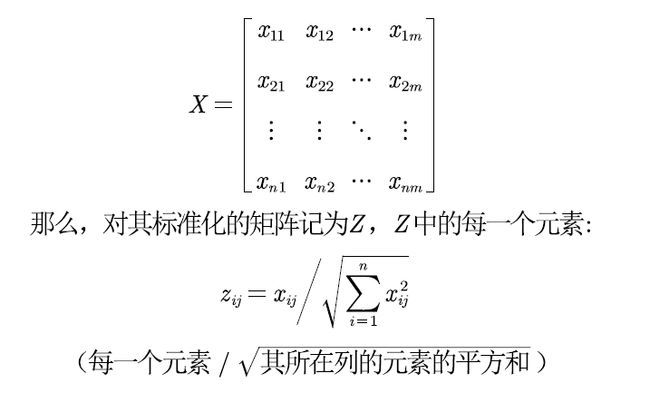
标准化处理

为了消去不同量纲的影响，需要对已经正向化的矩阵进行标准化处理。

---

如何计算得分

---

TOPSIS的流程

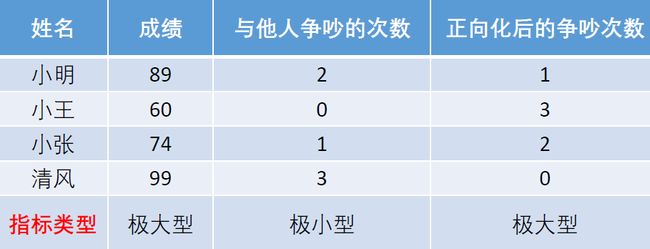
第一步：原始矩阵正向化

最常见的四种指标:

指标名称	指标特点	例子
极大型指标	越大越好	成绩、GDP增速
极小型指标	越小越好	费用、污染程度
中间型指标	越接近某个值越好	水的PH值
区间型指标	落在某个区间最好	体温

所谓的原始矩阵正向化就是将所有的指标类型统一转换为极大型指标

极小型-->极大型

公式: $$ max(xi) - x $$ 或者都是整数的话: $$ 1/x $$

中间型-->极大型

{xi}是一组中间型序列，且最佳的值为xbest

公式: $$ M = max{(|xi - xbest|)}, xi = 1 - |xi - xbest|/M $$

区间型-->极大型

{xi}是一组区间型指标序列，且最佳的区间为[a,b]

公式: $$ M = max({a - min{(xi)},max{(xi)} - b}) $$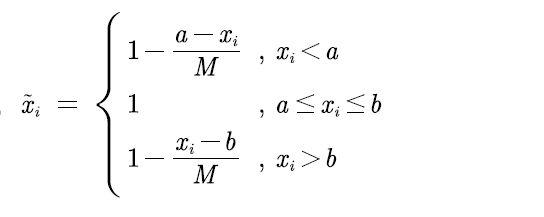

---

正向化矩阵标准化

如图：

计算得分并归一化

代码部分

第一步：把数据复制到工作区

clear;clc
load data_water_quality.mat
X = data_water_quality
%进行初步处理,得到行与列
[n,m]  = size(X)

第二步，判断是否需要正向化

%%topsis.m
disp['共有' num2str(n) '个评价对，象' num2str(m) '个评价指标' ]


%确定哪几列需要正向化
judge = input('请输入是否需要正向化,0代表不需要，1代表需要  ')

if judge == 1
    %记录需要正向化的列
    Position = input('输入需要处理的列数，比如[1,2,3]')
    %记录对应要处理列的指标类型
    Type = input('请输入对应的处理类型(1,极小型) (2,中间型) (3,区间型)')
    %对每一列进行正向化处理
    for i = 1 : size(Position,2)
        X(:,Position(i)) = Posivization(X(:,Position(i)),Type(i),i)
    end
    disp('正向化的矩阵X=')
    disp(X)
end

%%正向化矩阵标准化
stand_X = X ./ repmat(sum(X .* X) .^ 0.5,n,1)
disp('标准矩阵stand_X = ')
disp(stand_X)

%%标准矩阵归一化，计算得分
D_P = sum(((stand_X - repmat(max(stand_X),n,1)).^2),2).^0.5
D_N = sum(((stand_X - repmat(min(stand_X),n,1)).^2),2).^0.5
S = D_    n ./ (D_P + D_N)
%归一化
S = S / sum(S)

%%Posivization.m
function [output] = Posivization(x,type,i)
    if type == 1 %极小型
        disp(['第' num2str(i) '列式极小型，正在正向化'])
        output = Min2Max(x) %调用Min2Max函数来完成正向化
        disp(['第' num2str(i) '列式极小型正向化完成'])
    elseif type == 2 %中间型
        disp(['第' num2str(i) '列式中间型，正在正向化'])
        best = input('请输入最佳的那一个值')
        output = Mid2Max(x,best)
         disp(['第' num2str(i) '列式中间型正向化完成'])
    elseif type == 3 %区间型
        disp(['第' num2str(i) '列式区间型，正在正向化'])
        a = input('请输入区间的下界')
        b = input('请输入区间的上界')
        output = Inter2Max(x,a,b)
        disp(['第' num2str(i) '列式区间型正向化完成'])
    else
        disp('输入的类型错误，请检查')
    end
end

%%Min2Max.m
function [output] = Min2Max(x)
    output = max(x) - x
end

%%MidMax.m
function [output] = Mid2Max(x,best)
    output = 1 - abs(x - best)/max(abs(x-best))
end

%%Inter2Max.m
function [output] = Inter2Max(x,a,b)
    M = max(a - min(x),max(x) - b)
    output = zeros(size(x,1),1)
    for i = 1 : size(x,1)
        if x(i) < a
            output(i) = 1 - (a - x(i))/M
        elseif x(i) > b
            output(i) = 1 - (x(i) - b)/M
        else
            output(i) = 1;
        end
    end

end

本文由博客一文多发平台 OpenWrite 发布！