【数学建模】(3)插值模型 精解+代码
插值模型
-
概述
实际生活中,我们会使用各种各样的函数。对于y=exp(sinx)等难以计算、比较复杂的函数,我们希望找到一个近似的替代函数来方便计算y的粗略值。我们需要用一个比较简单的函数y=y(x)来近似代替数据,或近似代替函数y=f(x),使得:y(xi) = f(xi),i = 0,1,2,…,n,称y=y(x)为函数y=f(x)在点x0,x1,…,xn处的插值函数。 -
插值法的基本原理
求过已知有限个数据点(插值节点)的近似函数(插值函数)。 -
插值模型
1)范围:当数据量不足,需要补充,且认定已有数据可信时,通常利用函数插值方法建立插值模型。
2)目标:根据一组观测数据寻找函数关系。
3)具体方法

3.1 一维插值
3.1 线性模型
3.2 插值法的分类
a,若$P(x)$是次数不超过n的代数多项式,即$P(x)=a_{0}+a_{1}x+...+a_{n}x$
b,若$P(x)$是分段多项式,就成为分段插值
c,若$P(x)$是三角多项式,就成为三角插值,
function y = lagrange(x0,y0,x)
ii = 1:length(x0);
y = zeros(size(x));
for i = ii
ij = find(ii~=i);
yi = 1;
for j=1:length(ij), y1 = y1.*(x-x0(ij(j)));
end
y = y+y1*y0(i)/prod(x0(i)-x0(ij));
end
注意:
高次插值会产生龙格现象,即在两端处波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下,不要轻易使用高次插值
3.2分段线性插值模型
作用:提高插值精度
概念:给出x,在与之相邻的两点之间构造函数,寻找
分段二次插值:选取跟节点x最近的三个节点 x i − 1 , x i , x i + 1 x_{i-1},x_{i},x_{i+1} xi−1,xi,xi+1进行二次插值,即在每一个区间 [ x i − 1 , x i + 1 ] [x_{i-1},x_{i+1}] [xi−1,xi+1]上,取:
f ( x ) f(x) f(x) ≈ \approx ≈ L 2 ( x ) = L_{2}(x)= L2(x)= ∑ k = i − 1 i + 1 \sum_{k=i-1}^{i+1} ∑k=i−1i+1
φ \varphi φ ( x ) (x) (x) = ∑ i = 0 n \sum_{i=0}^n ∑i=0n y i y_{i} yi l i l_{i} li ( x ) (x) (x),其中

3.3 Lagarange插值(抛物插值、二次插值)
对给定的n个插值点x1,x2,⋯,xnx1,x2,⋯,xn及对应的函数值y1,y2,⋯,yny1,y2,⋯,yn,利用构造的n-1次Lagrange插值多项式,则对插值区间内任意x的函数值y可通过下式求的:
互异的三点联立得到带入模型: P ( x ) P(x) P(x) = a 2 x 2 a_{2}x{^2} a2x2 + a 1 x a_{1}x a1x + a 0 a_{0} a0
几何意义:
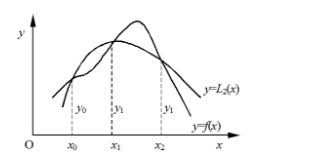
化简后得到的插值函数:

function y = lagrange(x0,y0,x)
ii = 1:length(x0);
y = zeros(size(x));
for i = ii
ij = find(ii~=i);
yi = 1;
for j=1:length(ij), y1 = y1.*(x-x0(ij(j)));
end
y = y+y1*y0(i)/prod(x0(i)-x0(ij));
end
例一:给出f(x)=ln(x)的数值表,用Lagrange计算ln(0.54)的近似值。
>> x=[0.4:0.1:0.8];
>> y=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144];
>> lagrange(x,y,[0.54,0.55,0.78])
ans =
-0.6161 -0.5978 -0.24843.4 分段三次(Hermite)插值
许多实际问题不但要求插值函数j(x)在插值节点处与被插函数f(x)有相同的函数值j(xi)=f(xi) (i=0,1,2,…,n), 而且要求在有些节点或全部节点上与f(x)的导数值也相等,甚至要求高阶导数值也相等,能满足这种要求的插值问题就称为Hermite插值。

Hermite插值公式:

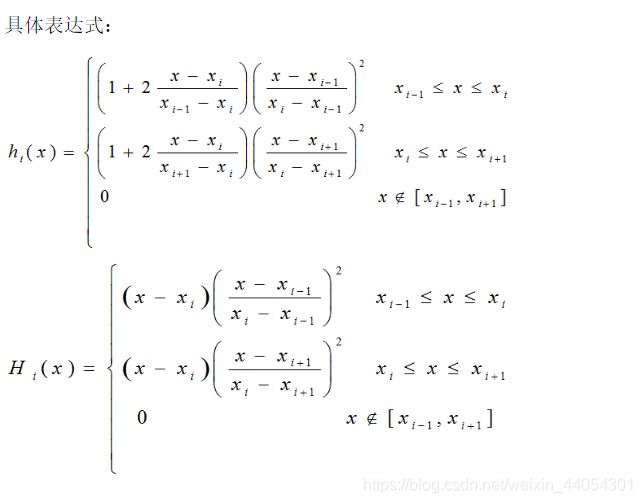
MATLAB实现:
hermite.m
function y=hermite(x0,y0,y1,x)
n=length(x0); m=length(x);
for k=1:m yy=0.0;
for i=1:n h=1.0; a=0.0;
for j=1:n
if j~=i
h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;
a=1/(x0(i)-x0(j))+a;
end
end
yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));
end
y(k)=yy;
end例二:对给定数据,试构造Hermite多项式求出sin0.34的近似值。
>> x0=[0.3,0.32,0.35];
>> y0=[0.29552,0.31457,0.34290];
>> y1=[0.95534,0.94924,0.93937];
>> y=hermite(x0,y0,y1,0.34)
y =
0.3335
>> sin(0.34) %与精确值比较
ans =
0.3335例3:
>> x=[0.3:0.005:0.35];
>>y=hermite(x0,y0,y1,x);
>> plot(x,y)
>> y2=sin(x);
>>hold on
>> plot(x,y2,'--r')3.5 n维数据的插值
p = interpn(x1,x2,…,xn,y,new_x1,new_x2,…,new_xn,method)
%x1,x2,…,xn是已知样本点的横坐标
%y是已知样本点的纵坐标
%method是要插值的方法
%'linear’线性插值(默认算法)
%‘cubic’:三次插值
%‘spline’:三次样条插值法(最为精准)
%‘nearest’:最邻近插值算法
% n维数据插值
x = -pi:pi;y = sin(x);
new_x = -pi:0.1:pi;
p = spline(x,y,new_x);
%等价于p = interpn(x,y,new_x,'spline');
figure(3);
plot(x,y,'o',new_x,p,'r-')
%线方式: -实线 :点线 -.虚点线 --波点线
%点方式:.圆点 +加号 *星号 x x形 o小圆
%颜色: y黄 r红 g绿 b蓝 w白 k黑 m紫 c青
例子:
%人口预测
population=[133126,133770,1224413,135069,135738,136427,137122,137866,138639,139538];
year = 2009:2018;
p1 = pchip(year,population,2019:2021)%分段三次埃尔米特插值预测
p2 = spline(year,population,2019:2021)%三系样条插值预测
figure(4);%对图进行命名
plot(year,population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','SouthEast')


