动手学深度学习笔记---4.3 解决过拟合_权重衰减与Dropout

一、权重衰退（Weight_decay）

正则限制

针对模型训练时出现的过拟合问题，限制模型容量是一种很好的解决方法，目前常用的方法有以下两种：

1. 缩小模型参数量，例如降低模型层数，使得模型更加轻量化，$L1$正则化
2. 通过限制参数值的选择范围来控制模型容量，$L2$正则化：
   • 使用均方范数作为硬性限制，即对于参数 $w,b$，假设其损失函数为 $l(w,b)$，则其优化目标为 $minL(w,b)subjectto||w|{|}^2\le \theta$
     • 在上述约束中通常不对 $b$进行约束，因为 $b$是针对 $0$点的偏移，且在实际中，限不限制并无区别。
     • $\theta$越小时，正则项的约束越强。
   • 使用均方范数作为柔性限制，通常来说，硬性限制的优化较为困难，因此通常采用柔性限制方法，即对于每一个 $\theta$均可找到一个 $\lambda$ 使得之前的硬性限制目标函数等价于： $minl(w,b)+\frac{\lambda }{2}||w|{|}^2$，可用拉格朗日乘子证明。
     • 正则项的重要程度通过超参数 $\lambda$ 进行控制，当 $\lambda =0$时，整个正则项不起作用，相当于 $\theta$ 趋向于无穷大时；当 $\lambda \to \infty$,等价于 $\theta \to 0$，渐渐使得$w^{\ast }\to 0$。

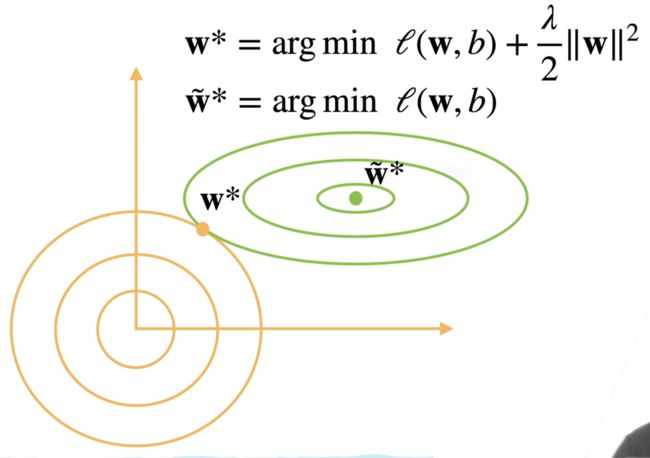
上图中，绿线部分为$L(w,b)$,在未引入正则惩罚项 $\frac{\lambda }{2}||w|{|}^2$ 时， $L$的最优解在圆心（绿点）处，而引入正则惩罚项后，绿点处的值相对于黄线部分来说非常大，此时不再是最优解。

当 ${\tilde{w}}^{\ast }$向原点处移动时，$L(w,b)$的值会增大，但惩罚项的值会缩小（离原点越近，正则项越小）。因此在绿点处，惩罚项对最优点的拉动力大于 $L(w,b)$ 的拉力，使得最优点逐渐移动到黄点位置，假设在此时，$L(w,b)$和惩罚项达到平衡，两侧的减少程度不足以满足另一项目的增加程度，此时达到最优。在这个过程中，$w$的绝对值不断降低，但不会像 $L1$正则化那样降低到 0，达到稀疏矩阵的效果。在这个过程中，越小的参数就会带来越简单的模型。

1.“为什么越小的参数值会带来越简单的模型？”

答： 一方面，较大的参数值会放大相似输入之间的差异，使得网络对训练数据敏感，从而出现过拟合现象，而小权重缩小了这种差异，从而提供了更好的泛化性。另一方面，越复杂的模型，越倾向于拟合全部样本，甚至异常样本，此时这种拟合会使得函数曲线变化剧烈，因此复杂的模型往往是过拟合的结果，其参数值就会较大。

2.“为什么切点处是最小值？”

答： 采用拉格朗日乘子法求解约束极值问题时，例如 $minL(w,b)subjectto||w|{|}^2\le \theta$，通常会引入拉格朗日乘子构建新的函数 $L(w,b,\lambda )=L(w,b)+\lambda g(w)$，然后通过求解下述方程组，可得最优解：

$\{\begin{array}{l}{▽}_{w}L(w,b,\lambda )=L_w^{\prime }(w,b)=0\\ {▽}_{b}L(w,b,\lambda )=L_b^{\prime }(w,b)=0\\ L_{\lambda }^{\prime }=g(w)=0\end{array}$

当曲面 $L(w,b)$即图中绿色等高线部分与曲线 $g(w)$即图中黄色部分相切时，切点即为最优解 $P$，因为二者相切时，约束曲线 $g(w)$ 在 $P$ 处法向量 $▽g$与该处目标函数的梯度 $▽L$相等且反向（共线），也就是$L(w,b)$和惩罚项达到平衡时。

参数更新法则

未引入惩罚项时， $w$的梯度为 $\frac{\partial L(w,b)}{\partial w}$，时间 $t$ 处更新参数公式为 $w_{t+1}=w_t-\eta \frac{\partial L(w,b)}{\partial w}$。
因此引入惩罚项后，$w_t$前增加了 $(1-\eta \lambda )$项目，通常 $\eta \lambda <1$,使得每一次更新时，当前的权重 $w_t$会进行一次缩小，这种情况就是 权重衰退。

总结：

• 权重衰退通过 $L2$ 正则项使得模型参数不会过大，从而控制模型复杂度。
• 正则项权重是控制模型复杂度的超参数。

代码实现：

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

初始化模型参数，并手动生成训练样本数为20，测试样本数为100，输入维度为200，batch_size为5的数据集，过小的训练样本集与过大的输入维度，可以使得模型过拟合效果更加明显，数据集的生成公式为：
$y=0.05+{\sum }_{i=1}^{d}0.01x_i+ϵwhereϵ\sim N(0,0.01^2)$

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)    # 生成满足 y = Xw + b + noise的值
train_iter = d2l.load_array(train_data, batch_size)         # 按batch_size将训练数据划分为iter
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

对模型参数进行初始化，w满足正态分布，b为全零矩阵

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定义 L2 惩罚项，为方便修改 $\lambda$ 值，不将该超参数写入函数内。

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2      # ||w||^2 / 2

训练代码实现

def train(lambd):
    w, b = init_params()
    # 模型为一个简单的线性回归函数，loss函数为均方误差MSE
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss     
    num_epochs, lr = 100, 0.003     # 定义epoch与学习率
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])     # 绘制图像
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            # L = L(w,b) + lambda / 2 * ||w||^2
            l = loss(net(X), y) + lambd * l2_penalty(w)         
            l.sum().backward()      # 反向传播
            d2l.sgd([w, b], lr, batch_size)     # 采用SGD优化函数作为优化器
        if (epoch + 1) % 5 == 0:
            # 每5轮在图像上绘制出一个最新的loss点
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

train(lambd=0)

此时惩罚项并未发挥作用，随epoch增加，train_loss与test_loss之间的差距越来越大，此时模型发生了过拟合。

train(lambd=3)

此时可以看到，随epoch的增加，train_loss与test_loss之间的差距开始缩小，证明增加惩罚项后，模型的过拟合现象得到缓解。

train(lambd=10)

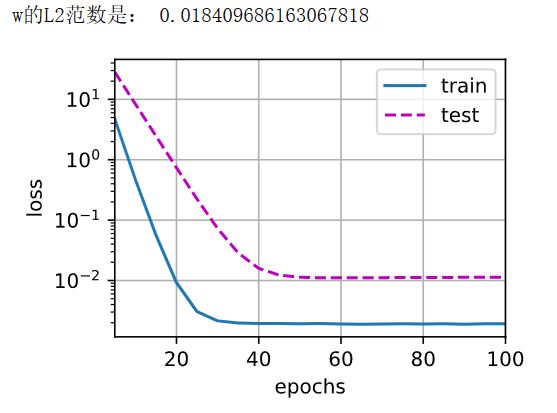
相较于 $\lambda =3$，此时模型的train_loss与test_loss曲线间的差距进一步减少，并且都发生了很好的收敛，有效缓解了过拟合现象。

train(lambd=100)

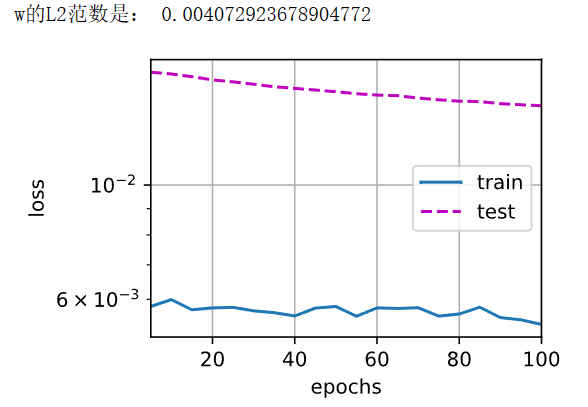
再次增大 $\lambda$后，w的L2范数降低到非常小的值，此时发现train_loss与test_loss之前趋于稳定。

def train(epoch_iter):
    lambd = 0
    num_epochs, lr = 100, 0.003     # 定义epoch与学习率
    animator = d2l.Animator(xlabel='lambd', ylabel='GAP', yscale='log',
                            xlim=[5, num_epochs], legend='GAP')     # 绘制图像
    for e_iter in range(epoch_iter):
        w, b = init_params()
        net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
        for epoch in range(num_epochs):
            for X, y in train_iter:
                # 增加了L2范数惩罚项，
                # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
                l = loss(net(X), y) + lambd * l2_penalty(w)         # L = L(w,b) + lambda / 2 * ||w||^2
                l.sum().backward()      # 反向传播
                d2l.sgd([w, b], lr, batch_size)     # 采用SGD优化函数作为优化器
        
        lambd = lambd + 10
        animator.add(lambd, (d2l.evaluate_loss(net, test_iter, loss) - d2l.evaluate_loss(net, train_iter, loss)))   

train(epoch_iter=10)

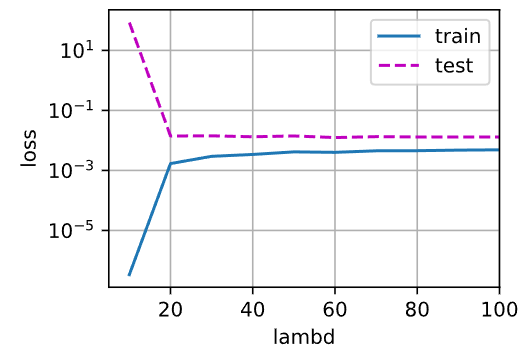
可以看到，从上图中可以看到，随 $\lambda$ 的增加，train_loss与test_loss之间的差距不断缩小，直到 $\lambda =80$左右时，达到稳定。

二、Dropout

正如一个好的身体可以抵抗多种病毒，一个好的模型也需要做到对多种输入数据所带来的扰动鲁棒。以图片为例，不管图中加入多少噪音，在模糊一点的情况下，人依旧能识别出这张图片，忽略噪声带来的干扰。深度学习模型也是如此。

因此，一个好的模型能在未知数据上具备很好的泛化性，需要满足两点要求：

• 简单性： 经典泛化理论认为，为了缩小训练和测试性能之间的差距，应该以简单的模型为目标。参数的范数也可以理解为模型的简单性度量。
• 平滑性：一个好的函数不应对输入时的微小变化过分敏感，即对于模型推理时，添加一些噪声到数据中，对于模型的结果应该是基本无影响的。

克里斯托弗·毕晓普等人证明，对于数据来说，使用有噪声的数据，实质上等价于一个Tikhonov 正则，属于在数据中增加噪音的方法。用数学证实了“要求函数光滑”和“要求函数对输入的随机噪声具有适应性”之间的联系。

丢弃法则与上述数据噪音不同，丢弃法不在输入时加噪音，而是在层之间增加无差别噪音。 因为当训练一个有多层的深层网络时，注入噪声只会在输入-输出映射上增强平滑性。

无差别加入噪音

对于数据中加噪音的方法，输入值$x$增加噪音得到结果$x^{\prime }$，通常希望加入噪音后，数据的期望不变，即 $E[x^{\prime }]=x$。

而丢弃法则是对于概率$p$，为每个元素增加如下扰动：

$x_i^{\prime }=\{\begin{array}{l}0withp\\ \frac{x_i}{1-p}otherwise\end{array}$

此时仍满足期望不变性。

$E[x_i^{\prime }]=p\ast 0+(1-p)\ast \frac{x_i}{1-p}=x_i$

丢弃法的使用

通常在训练使用时，Dropout常被作用于全连接层的隐藏层上：


在使用Dropout后，隐藏层中的部分节点可能被随机抛弃，设置为0。而且该过程是一个随机的过程，每次Dropout时所抛弃的节点不一定相同。

但是在推理时，通常不会使用Dropout，因为其本质也可理解为一个正则项，而正则项因为影响模型参数的更新，通常只在训练时使用。

因此在预测时，参数无需变化，Dropout输出的时其输入本身，即 $h=Dropout(h)$ ，从而保证确定性的输出结果。

而在早期Hinton提出的Dropout中，具体思路与当今方法并不相同，Hinton将之理解为一个类似集成学习的ensemble问题，通过将神经网络中节点随机去掉后，形成多个不同的子神经网络，然后集成这些网络结果做一个平均，获得最终结果。

后续实验中发现，Dropout的结果很符合正则项的结果，因此人们逐渐将其转为正则问题看待。（玄学）

总结：

• 丢弃法将一些输出项随机设置为0，来以此控制模型复杂度
• 丢弃法通常作用于多层感知机（全连接层）的隐藏层输出上
• 丢弃概率$p$是用于控制模型复杂度的超参数，类似权重衰退中的$\lambda$，通常设置为0.5
  

代码实现

import torch
from torch import nn
from d2l import torch as d2l

# 定义Dropout层
def dropout_layer(X, dropout):
    # 丢弃概率不在(0，1)之间时，触发断言退出函数
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
        # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
        # 生成mask矩阵，根据该矩阵将对应位置x值置0
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

# 定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

# 设置丢弃率
dropout1, dropout2 = 0.2, 0.5
# 模型定义
class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    # 前向传播
    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

# 模型训练与测试
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

交换两个丢弃率后，图像如下：


可以看到将丢弃率由 【0.2，0.5】更换为 【0.5，0.2】后，test_loss发生了一些波动，但最终结果无显著差异。

为放大这一问题，将丢弃率由【0.1，0.9】修改为【0.9，0.1】，图像如下：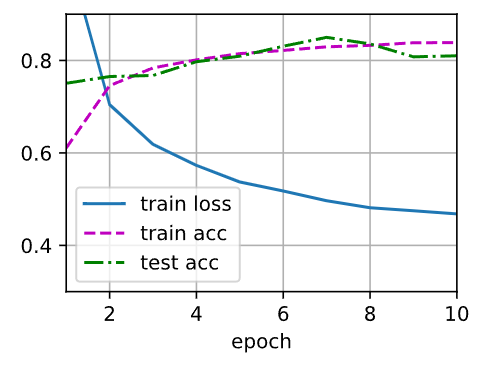


可以看到模型出现了明显的过拟合现象，train_loss也下降缓慢。

初步猜测，由于多层感知机中采用全连接方法，层数越多提取的特征越精细，模型学习到过于精细的特征后，就会对微小特征过分敏感，产生过拟合现象。而【0.1，0.9】抛弃率Dropout的使用，使得模型少量抛弃了前期粗糙的部分冗余特征或噪声，大量抛弃精细特征，提高了模型鲁棒性。而【0.9，0.1】抛弃率的使用，会使得模型大量丢弃前期采集到的特征，降低了模型鲁棒性，致使test_acc 不增反减，train_loss也过高导致无法运行，改为【0.8，0.2】时仍会出现类似问题。

个人认为，过高的抛弃率对多层感知机的第一层影响最大，大量信息的丢失会使得模型产生很差的训练效果。但同样的高抛弃率对第二个隐藏层（也可能是最后一个隐藏层）影响较小，产生类似减少一个隐藏层的效果，反而降低了模型复杂度。