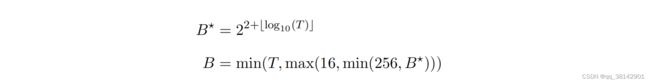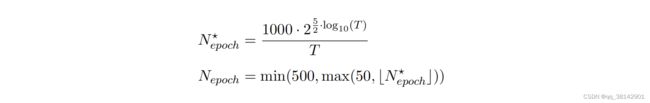【论文阅读】NeuralProphet: Explainable Forecasting at Scale

前言

该模型的官网见该连接，其论文获取，最新版本相关情况，以及github入口，官方使用文档均可以从该入口获取。
言归正传，本文模型延续了prophet的可扩展，解释性强，与使用友好的优点，同时增加了神经网络部分（包括自回归网络与协变模块两种网络），与基于pytorch后端的实现可以随着深度学习算法的更新进行更新，这部分弥补了prophet模型对上下文信息利用的缺失（通常对近期未来预测有重要作用，非线性动态拟合差，以及prophet基于stan（统计概率编程语言）实现难以与深度学习模型进行结合以及更新扩展的问题。本文在后面的内容对新模型的原理构成进行了阐述，以及在若干数据上，短中期时许预测上对本文模型与prophet进行了对比。

1、Neural Prophet 模型

1.1 模块组成

其整体模型组成见公式（1），其中的模块分别是，趋势模块，周期性模块，事件模块，未来已知的外源数据的回归效应模块，基于过去观测值的自回归模块，以及基于外源数据给定lag的回归模块。这些模块均可单独配置与组合，当所有模块均关闭时，只有一个静态截距参数拟合为趋势模块，如y=p0,其中p0为常数作为趋势模块。接下来具体介绍每一个模块。

1.1.1 趋势模块

经典的趋势为线性函数，业务理解为历史t0到t1的增长率，以及对应的截距，其公式如（2），简单明了；当日现实中增长率可能随着时间的变化而变化，其中截距也可能随着时间的变化而变化，为了拟合实际情况，提出了分段线性趋势函数，从业务理解来说由历史给定若干变点，在变点处增长率与截距发生变化，为了确保各分段的连接，对截距设置了限制ρj = −cjδj。给定初始的增长率δ0与截距p0，其分段趋势如公式（3）。其中变点数可以进行自动学习得到，也可以人为进行指定，其趋势参数类似prophet。其中为了避免过拟合，最后一段趋势，默认由15%的训练集得到，为了预测未来，最后的增长趋势将以线性的方式扩展到未来。

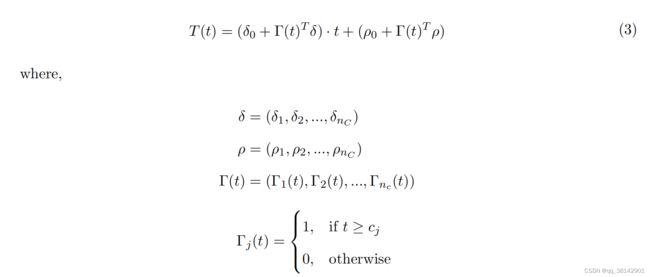
1.1.2 周期性

其原理与prophet一致，均采用傅里叶变换函数实现，其周期支持非整数，支持多个周期同时存在的场景，每个周期支持不同的观测数进行定义，周期也有加法或者乘法模型选择，当前算法支持用户自定义的周期，也可以使用框架内置的周期，分别是年效应k=6,p=365.35；周效应k=3,p=7；日效应k=6,p=1。为了防止过拟合，观测数据长度最好是所设置周期的2到3倍，如开启年效应，观测数据最好是有2到3年及以上的长度。

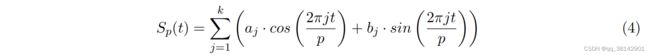
1.1.3 自回归

经典的自回归函数是由截距c，过去的p个观测值，乘以权重，相加再加上白噪声得到，其公式见下方。可以看到经典的自回归函数是线性的，且每次只能进行单步预测，当进行多步预测时，需要对应的拟合模型多次。因此本文中采用【Triebe, O., Laptev, N., & Rajagopal, R. (2019). Ar-net: A simple auto-regressive neural network for time-series.arXiv:1911.12436.】提出的自回归神经网络AR- Net。该网络可以实现训练模型一次输出多步预测，可以实现线性，与非线性拟合，以及添加惩罚项和稀疏网络训练。

在使用该网络时，首先要决定的一个重要参数就是输入的观测数p，这很难决定，通常是设置为内置周期的两倍或者外推期的两倍，比如有周效应，则p设置为14；或者外推期为10，则p设置为20。当同时对回归使用正则以获取稀疏AR网络的时候可以保守一点将p设置的大一点。
该模型里，默认的回归模块是最简单的线性回归网络，没有隐藏层，它是只有一层无激活函数，p个输入，h个输出的神经网络；如此一来每个输出的权重系数与输入均是一一对应的，可以很直观的看到各个输入对输出的贡献。
当使用多层回归网络时，其解释性下降，我们只能通过第一层每个输入的权重绝对值和的对比大致观测到输入的观测值对输出的相对重要性。其隐藏层激活函数使用的是Relu，最后输出层没有激活函数与偏差项，默认连接为全连接。当加入惩罚项时，可以得到一个稀疏的回归网络。稀疏网络上不为零的权重对应的输入位置，可以通过这些位置上的权重信息去研究其不同的观测值组合是如何影响预测的。

1.1.4 滞后回归

滞后回归体现了外源数据过去的观测值与目标数据的相关性。输入p个历史协变量，经过AR网络获得h步输出，其需要关注的方面与自回归部分类似，这里不再赘述。

1.1.5 未来回归

该部分要求外源数据历史与未来均为已知，给定回归数，可以选择加法或者乘法模式，默认采用加法模式。

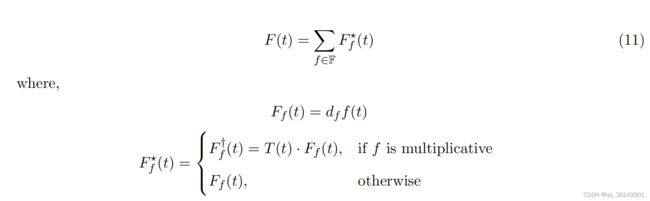
1.1.6 事件与节假日

该部分与prophet保持一致，同样支持加法与乘法模式，支持自定义事件，模型内置了国家节假日，需要配置的可以直接使用，支持两种输入数据格式进行事件配置，一是日期与事件名，二是日期，日期窗口以及事件名。

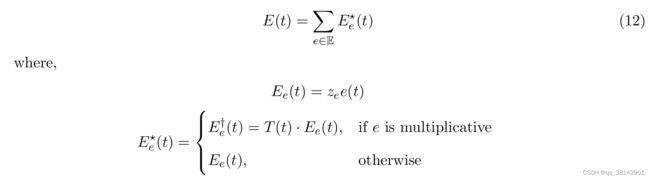
1.2 预处理

1.2.1 缺失值

缺失值在没有滞后变量使用的时候，问题不大，做扔掉处理就好。当有自回归类模块时，同样处理会导致h+p个样本丢失，由于h预测目标有缺失值和p个滞后数据里有缺失值。因此本文作者团队提出了填充机制来避免数据丢失，填充机制采用下方方法。
当没有明确缺失值时，事件配置默认填充为零，及默认该点无事件发生。模型里设计到真实值回归的模块，其填充机制均按下面的三步走进行填充。
第一步，缺失的值可以用相邻的两侧的值来近似，如缺失值等于两侧值的均值近似；在本文模型中，其两侧真值中间缺失值长度默认最多为10个（理论上缺失过多，其填充值失去代表性），超过10个时，执行完这一步缺失值仍然是空值状态。其中缺失值长度支持用户自定义。
第二步，执行完第一步仍然缺失的值，将采用中心滚动均值进行填充；中心滚动均值窗口为30，可填充最多20个连续缺失值，同样填充的缺失值长度支持用户自定义。
第三步，如果有超过30个连续的缺失值，停止填充机制，去掉所有缺失值。

1.2.2 标准化

本文模型支持对数据进行标准化，如果不设定，对于二值化数值使用minmax，其他默认使用soft。具体支持的方式如下表所示。

1.2.3 表式化

该部分处理是为了模型采用随机梯度下降法进行训练，处理后假装创造了一个独立且分布一致的数据集。

1.3 训练

1.3.1 损失函数

模型默认采用Huber Loss 函数，即MSE与MAE的组合，该损失函数对异常值的敏感度低，且可防止梯度爆炸。其阈值$\beta$=1，用户也可以选择MSE，或MAE，或者pytorch上的其它损失函数用于训练。

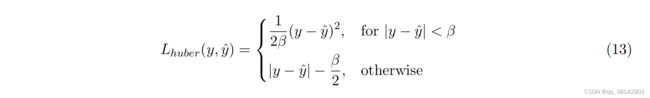
1.3.2 正则化

本文采用了权重绝对值的缩放和对数变换偏移作为一般正则化函数。其中$ϵ\in (0,\infty )$ 为偏移的倒数， $\alpha \in (0,\infty )$ 为对数变换的比例。$ϵ$控制权重参数的稀疏程度，$\alpha$控制权重值的大小；默认情况下，设置 $ϵ$=1,$\alpha$=1。
该正则可用于各模块之中，将其加入损失函数中，正常参与训练，反向传播；在未指定百分比下，正则默认在训练50%后由0逐渐线性增加至所配置强度。

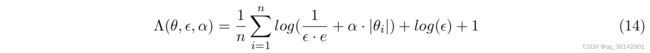
1.3.3 优化器

在prophet 中采用的是LGBF，在本文中，其训练的模块涉及到深度学习的算法，采用AdamW 优化算法，同时也提供回退选项，采用动量设置的随机梯度下降SGD，在部分测试中该算法拟合出来的模型表现更好，但是该算法有可能会发生不收敛的情况。当然也可以选择pytorch支持的其它优化算法。

1.3.4 学习率

本文选择对学习率的一段范围进行测试，根据数据集时序长度T决定迭代次数，100+log10(10+T)*50,在设置好的批次下，学习率在$\eta \in (1e-7,1e+2)$范围内进行测试，除了开始的十次迭代与最后的5次迭代，中间采用较大的学习率进行迭代。为了提高可信度，取三次测试的均值作为最终使用的学习率。

1.3.5 批次大小

若没有指定，批次大小由数据集的时长T进行计算得到。

1.3.6 迭代次数

若没有指定，迭代次数由数据集的时长T进行计算得到。

1.3.7 计划

模型的超参数基本都是可以自动估计得到，通常这种方式得到的不是最优的参数，为了以防训练过程出现问题，本文采用‘1cycle’策略进行训练。具体是开始学习率采用的$\frac{\eta }{100}$,然后慢慢增大学习率，在30%训练进程时增大到$\eta$,在这之后学习率随着余弦曲线下降，到训练结束时，下降到$\frac{\eta }{5000}$。

1.4 后处理

1.4.1 评价

默认支持RMSE，MAE两种方式，用户也可以使用自己定义的指标。

1.4.2 预测输出代表含义

模型输出会包含每一个模块对应的列，如‘yhat3‘指的是基于三步前的数据预测当前时间点的预测值；再比如‘ar2’，是基于两步前的观测值，自回归模块对当前时间点的预测值。

2、总结

实验对比部分在这里就不详细展开了，总的来说首先通过人工构建对应不同模块的数据，与prophet进行效果与性能比较；之后再在真实的数据集上与prophet效果进行对比。
其中需要注意的点有，一在默认模型下（neural prophet 仅激活趋势模块与周期性模块），两者的效果差不多；当加入回归类模块，本文模型的表现明显要好于prophet，且在长的多步预测上其效果下降幅度不大。二、在性能比较上，同等资源下训练时间本文模型需要更长，但是预测阶段本文模型更快。三、本文模型在采用回归类网络时，对滞后数（lag)的设置以及神经网络的设置如隐藏层，其敏感度不大。四、根据应用与实验积累的经验，在小数据集（T《100）的场景与在有限资源下频繁训练小数据集的场景建议使用prophet。

结束语

到这里，这篇论文的核心内容就结束了，此文只做个人学习的笔记与理解记录，若有理解错误的地方，欢迎大家指正。