算法设计与分析复习--回溯法（二）

上一篇

算法设计与分析复习–回溯（一）

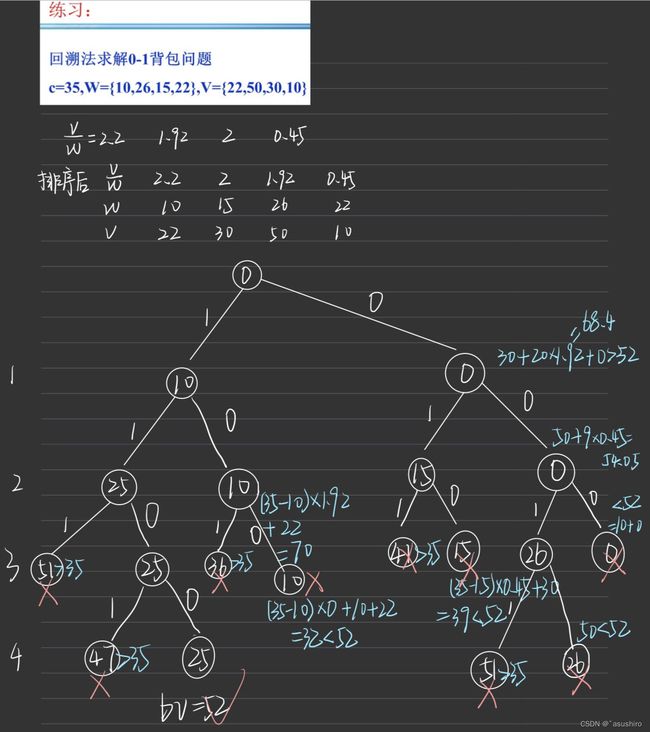
0-1背包问题

问题描述：给定n中物品和一个背包。物品 $i$ 的重量是 $w_i$ ，其价格为 $v_i$ , 背包容量为 $c$ 。 问如何选择装入背包中的物品，使得装入背包物品的总价值最大？

左剪枝：满足背包容量即可

右剪枝：右剪枝就是求剩余背包重量rw = c - cw中贪心背包的最优价值，由于允许部分装入，所以一定比0-1背包装的满价值更大，结果是剩余价值的一个上界，允许右剪枝的条件更加宽松。
$$rv=\sum v_j(不超过背包剩余重量的物品价值)+(背包剩余重量)\ast （不被放入的物品的单位价值）【部分装入的结果】$$
限界函数：
$$cv+rv>=bv$$

交换搜索顺序：由于用到了贪心背包，所以按照物品单价从大到小的方式进行搜索。

#include 
#include 
#include 

using namespace std;
typedef pair PII;

const int N = 110;

double w[N], v[N];
int n, c;
double cw, cv, bv;
vector ob, x;//x用来记录当前的搜索顺序
vector ans;//最优解，解只有一个，将这个迭代的解记录

bool cmp(PII x, PII y)
{
    return (x.second / x.first) > (y.second / y.first);
}

bool bound(int rw, int k)
{
    int i = k + 1;
    double rv = cv;
    //printf("cv: %.2lf rw: %d\n", cv, rw);
    while(i <= n && ob[i].first <= rw)
    {
        rw -= ob[i].first;
        rv += ob[i].second;
        i ++;
    }
    //printf("比值：%.2lf rw:%d\n", ob[i].second / ob[i].first, rw);
    if (i <= n) rv += (ob[i].second / ob[i].first) * rw;
    //printf("%d = %.2lf\n", k, rv);
    return rv >= bv;
}

void dfs(int k)
{
    if (k == n){
        if (cv > bv){
            bv = cv;//更新最优结果
            ans = x;
        }
        return;
    }
    
    if (cw + ob[k].first <= c)
    {
        cw += ob[k].first;
        x.push_back(ob[k]);
        cv += ob[k].second;
        dfs(k + 1);
        cv -= ob[k].second;
        x.pop_back();
        cw -= ob[k].first;
    }
    if(bound(c - cw, k))
    {
        dfs(k + 1);
    }
}

int main()
{
    scanf("%d%d", &n, &c);
    
    for (int i = 0; i < n; i ++) scanf("%lf", &w[i]);
    for (int i = 0; i < n; i ++) scanf("%lf", &v[i]);
    for (int i = 0; i < n; i ++) ob.push_back({w[i], v[i]});
    
    sort(ob.begin(), ob.end(), cmp);
    
    dfs(0);
    
    puts("对应物品的重量和价值:");
    for (auto i : ans)
        printf("{%d, %d} ", (int)i.first, (int)i.second);
    puts("\n最优价值：");
    printf("%d", (int)bv);
    return 0;
}

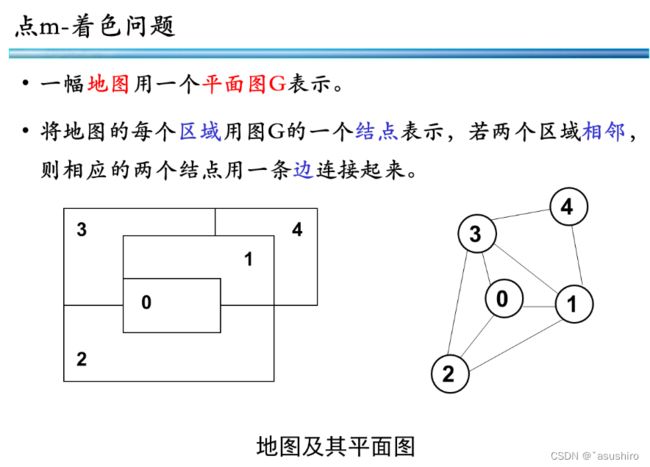
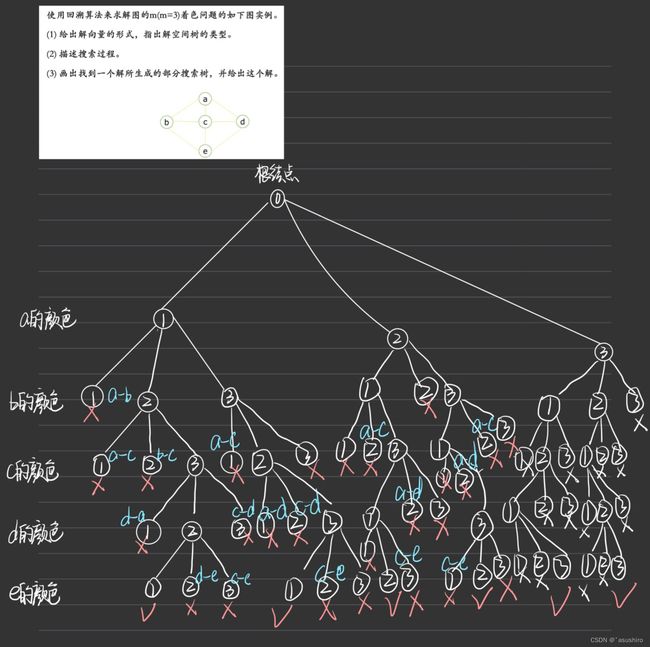
图着色问题

洛谷P2819 图的 m 着色问题

左剪枝：一条边两个节点的颜色不能相同。

#include 

using namespace std;

const int N = 110;

int color[N], g[N][N];
int n, m, ans = 0;

bool constrain(int k) {
    for (int i = 1; i <= n; i++) {
        if (g[k][i] == 1 && color[k] == color[i]) {
            return false;
        }
    }
    return true;
}

void dfs(int k) {
    if (k == n + 1) {
        ans++;
        return;
    }

    for (int i = 1; i <= m; i++) {
        int prevColor = color[k]; // Backup current color需要先将之前的颜色备份起来否则无法恢复, 后面用的时候需要判断所以不能只覆盖掉
        color[k] = i;
        if (constrain(k)) {
            dfs(k + 1);
        }
        color[k] = prevColor; // Restore the color after backtracking
    }
}

int main() {
    int k;
    cin >> n >> k >> m;

    for (int i = 0; i < k; i++) {
        int u, v;
        cin >> u >> v;
        g[u][v] = g[v][u] =1;
    }

    dfs(1); // Start from vertex 1

    cout << ans << endl;

    return 0;
}

只需找一个，我都找了（怒）

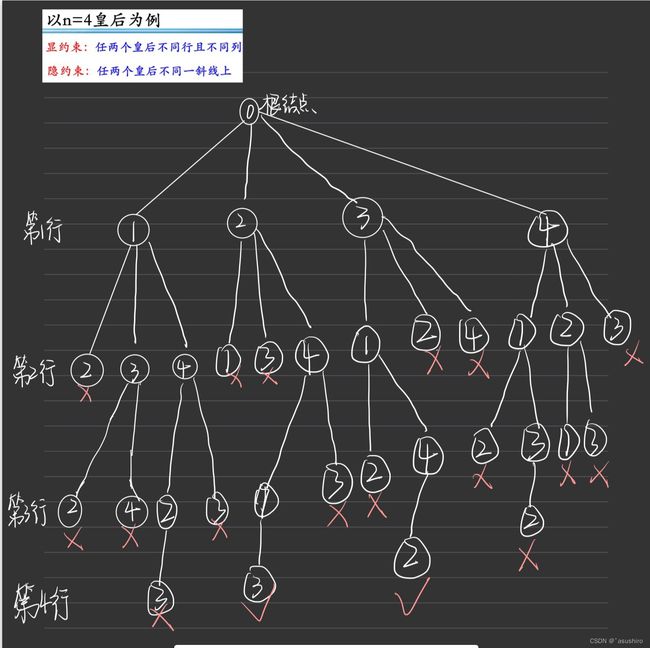
n皇后问题

AcWing 843. n-皇后问题

问题描述：皇后问题要求在一个nxn的棋盘上放置n个皇后，使得他们彼此不受攻击。n皇后问题要求寻找在棋盘上放置这n个皇后的方案，使得她们中任意两个都不在同一行、同一列或同一斜线。

#include 
#include 
#include 

using namespace std;

const int N = 10;

char g[N][N];
int x[N];//x[i] 表示第i行第j列放皇后
int n;

bool constrain(int k, int j)
{
    for (int i = 0; i < k; i ++)
        if (x[i] == j || abs(k - i) == abs(j - x[i]))
            return false;
    return true;
}

void dfs(int k)
{
    if (k == n)
    {
        for (int i = 0; i < n; i ++)
            puts(g[i]);
        puts("");
        return;
    }
    
    for (int i = 0; i < n; i ++)
    {
        if (constrain(k, i))
        {
            x[k] = i;
            g[k][x[k]] = 'Q';
            dfs(k + 1);
            g[k][x[k]] = '.';
        }
    }
}

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n; j ++)
            g[i][j] = '.';
    dfs(0);
    return 0;
}

利用st数组实现排列树

#include 
#include 
#include 

using namespace std;

const int N = 10;

char g[N][N];
int x[N], n;
bool st[N];

bool constrain(int k, int j)
{
    for (int i = 0; i < k; i ++)
        if (abs(k - i) == abs(j - x[i]))
            return false;
    return true;
}

void dfs(int k)
{
    if (k == n)
    {
        for (int i = 0; i < n; i ++)
            puts(g[i]);
        puts("");
        return;
    }
    
    for (int i = 0; i < n; i ++)
    {
        if (!st[i] && constrain(k, i))
        {
            st[i] = true;
            x[k] = i;
            g[k][x[k]] = 'Q';
            dfs(k + 1);
            g[k][x[k]] = '.';
            st[i] = false;
        }
    }
}

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n; j ++)
            g[i][j] = '.';
    
    dfs(0);
    return 0;
}

下一篇

算法设计与分析复习–分支界限法