哈工大算法设计与分析之树搜索问题

1.背景

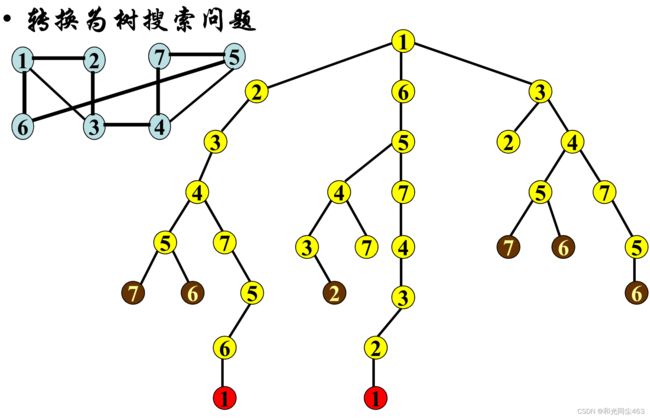
许多的问题,比如走迷宫,寻找哈密顿环,都可以转换成树搜索问题,对于已经走过的点是下一步选择的双亲,在实际操作中,以走迷宫为例我们可以对这些双亲进行标记,来判断是否出现死胡同,进而避免重蹈覆辙的错误。但是光是以这种直观的标记可能不是最优化的搜索策略,如何提前发现不满足问题解,需要设计相应的算法。

常规的方法包括:深度优先 广度优先

在常规方法的基础上,我们进行了优化

哈密顿环问题

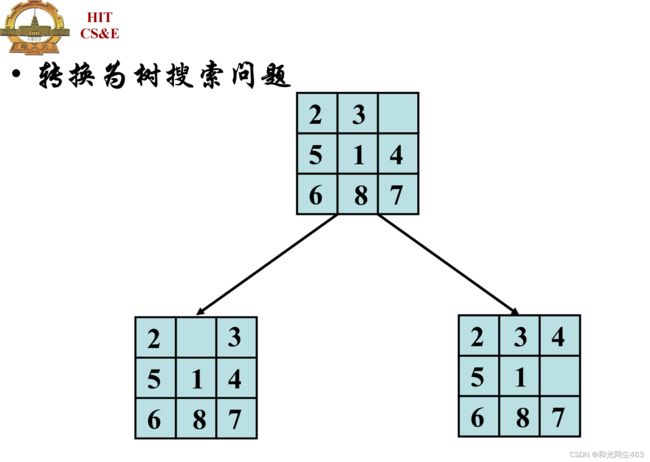
8-数码问题

 2.优化树的搜索策略

Hill-Climbing(爬山法)

解决的问题:

在深度优先搜索过程中, 经常遇到多个节点可以扩展的情况, 首先扩展哪个?

算法思想方法

策略:用贪心方法确定搜索的方向 使用启发式测度来判断拓展的次序。

用8-Puzzle问题来说明爬山策略的思想

这里的启发式测度是Wn也就是错误的方块个数

每次贪心的向Wn小的方向进行扩展

 算法实现

讨论和分析

回过头来看 爬山法 加以深入的理解 

 Best-First Strateges

基本思想

1. 结合了深度优先和广度优先的特点
2. 相比于hill-climbing爬山法而言,爬山法仅具有局部最优观念,而Best-First具有全局优化的观念,这就需要用到堆这种数据结构
3. 设计合理的评价函数,根据一个评价函数, 在目前产生的所有节点中选择具有最小评价函数值的节 点进行扩展.

 实现原理

仔细回想一下我们在最短路径算法时也用到了类似的搜索策略,从这个节点向外扩张,不断更新所有节点到达这个节点的最小代价,不断更新这个代价,重复这个过程,每次都选最短的路径进行扩张,期待每次最后能得到到该顶点的最短路径.

8-pullze问题实例 

 实现的过程就是如图展开的启发方式,实际中的搜索代价就是实际中展开的节点

从左向右，每次选择全局含有最小代价进行扩张,过程如下↓

1. 初始化
2. 然后展开第二行 3 3 4 4
3. 对最左边的3进行扩展发现是3 4 当前最小的是扩展完第三行第一个的3和第二行第二个的3 由于第三行第一个的三不能继续扩展,所以选择第二行第二个3进行扩展得到一个当前全局最优的2。
4. 再对第三行第三个2进行扩展得到全局最优的1
5. 再对1进行扩展,发现最优解,程序结束

复习：

对于传统算法如何对算法进行改进,从而让搜索代价(展开的次数更小呢)？

引入爬山法和Best-First来减少展开的次数

 Branch-and-Bound Strategy(分支界限方法)

引入背景

解决组合优化问题和缩小解空间

(100条消息) 组合优化问题_xiangrikui_ccl的博客-CSDN博客_组合优化问题

利用多阶段图问题说明分支界限方法

 问题求解

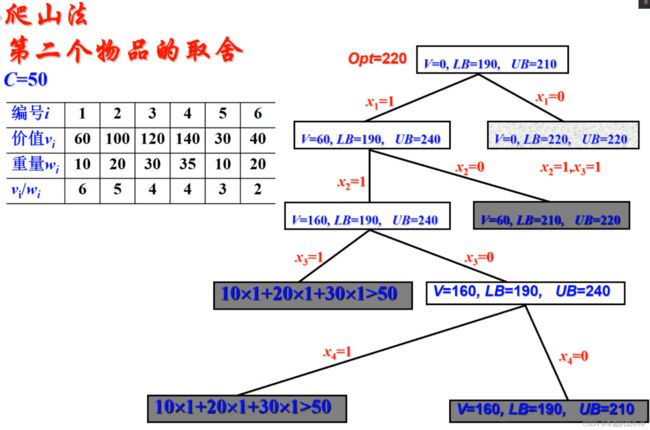
1. 如果采用爬山策略的话,就是进行一个深度优先会每一步选择当前扩展最小代价的方向进行延申.
2. 随着我们的延申可以得到一个可行解,但他未必是最优解,我们可以利用这个可行解,在延申其他的节点的过程中进行剪枝.
3. 当所有的解空间都被剪枝完之后我们可以得出结论5是最优解v0-v11-v23-v3
4. 在搜索过程中我们裁剪不能扩张的点或者不断发现新的最优解进而减小我们解的下界

 基本思想

 说白了就是用爬山法或者Best-First方法找到一个可行解 再利用这个可行解对其他扩展进行剪枝(分支界限法的关键) 在剪枝过程中可能发现更优解,从而更新剪枝的下界.

3.实例(example)

人员安排问题(简单直接用分支定界往往不能很好解决问题)

问题的定义和偏序关系的定义

对于员工集合P，员工集合会依据某个f来给出某种顺序，需要按该顺序P(i)进行工作安排。

对于工作集合J，可以进行偏序排序，有一个偏序来排列工作。

 

拓扑排序生成树表示

 拓扑排序生成伪代码

Input:偏序集合S, 树根root
Output:由S的所有拓朴排序序列构成的树

生成树根root
选择偏序集中没有前序元素的所有元素, 作为root的子节点
 For root的每个字节点v Do
    S=S-{v}
    把v作为根, 递归地处理S

 例题

偏序关系和代价矩阵如图所示

 这是一个组合优化问题,不能通过Hill-climbing和Best-First得到最优解，必须将所有可行解展开之后才能得到最优解。

具体执行过程如下,我分支界限采用的是爬山策略,读者也可以自行采用Best-First策略进行练习

 方法的不足与改进

不足

经过求解我们发现,用分支定界的方法不能相对于爬山法和Best-First方法，只减少了一次展开次数，对于优化也不起明显效果，有什么方法能提高剪枝的效果。

指派效果没有明显的偏差很难提前进行的剪枝,所以简单的选择分支定界并不合适

改进

无论哪一种指派,都有一个代价下界,对于每一行都有一个最小值

每行每列减去值的最小值使得出现每一行每一列都出现一个0 

例题

计算得到无论怎么安排代价的下界都是54,我们使用爬山法进行延申0-2-1-3-4得到可行解的代价下界是73,然后弹栈0-2-1-4-3得到可行解的下界是70，再向右进行拓展发现71<70,所以直接进行剪枝

所以我们发现分支界限法的使用也是有一些讲究的 ，如果进行简单的应用，往往不能更好的得到问题的解

旅行商问题

问题的定义

说白了 就是解决哈密顿环问题 哈密顿环:包含所有顶点 只有一个圈 所有顶点只有一条路径的环(可能不是很精准的定义,具体定义我忘了 大家可以翻看一下离散数学的教材)

实例和问题的求解

对于这样的一个矩阵我们得到了一个这样的结果 简单说明一下这个矩阵的含义,比如说f(1,2) 就是说我从1顶点到2顶点从类型上粗略分为两种路径选择,第一种是1-直接到2,第二种方法1-i,j,k....,2中间经过多个节点,那么我们现在想要做的是让不包含直接路径中,路径的值尽可能的大。如下图所示。我们找到了一个不直接包含4-6边的最大路径值,发现是32，那么就以是否取4-6为划分进行问题的求解。这样做的目的是当我们得到可行解的时候可以尽早地进行剪枝。

我们思考:在爬山法的过程中，我们先用先深的方法找到可行解，那么类似的，下图进相同的操作

通过上图的分析 我们把包含4 6 的边置为∞

然后递归地构造子树，重复1的过程

 当然0-1背包问题也可以转化成 树搜索问题 具体的求解大家可以一起思考和讨论

A*算法 

A*算法和分支界限法的比较

        -----分支界限策略是为了剪掉不能达到优化解的分支

        – 分支界限策略的关键是 “界限”

        – A*算法的核心是告诉我们在某些情况下, 我们得 到的解一定是优化解, 于是算法可以停止

        – A*算法试图尽早地发现优化解

        – A*算法经常使用Best-first策略求解优化问题

A*算法的关键,代价函数

– 对于任意节点 n

• g(n) ＝从树根到 n 的代价

• h*(n) ＝从 n 到目标节点的优化路径的代价

• f*(n) ＝ g(n) + h*(n) 是节点 n 的代价

– What is the value of h*(n) ?

• 不知道！

• 于是, f*(n) 也不知道

– 估计 h*(n)

• 使用任何方法去估计 h*(n) , 用 h(n) 表示 h*(n) 的估计

• h(n)<= h*(n) 总为真

• f(n) = g(n)+h(n)<= g(n)+h*(n) = f*(n) 定义为 n 的代价

举例

 

 

算法正确性的证明 

如何证明算法一定是最优解

A*算法是一种特殊的分支界限方法 

拓展和提高

https://zhuanlan.zhihu.com/p/54510444?utm_id=0

A*算法的小练习

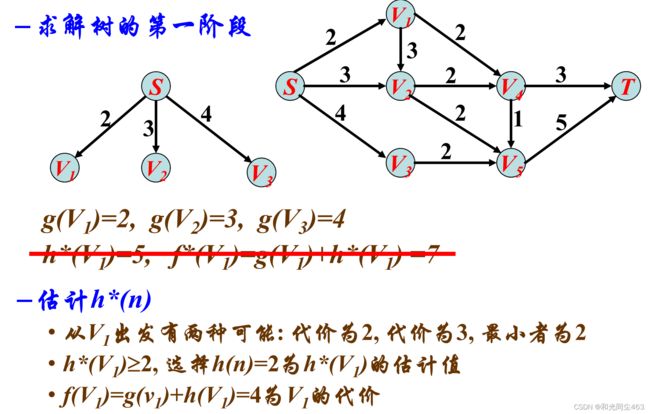
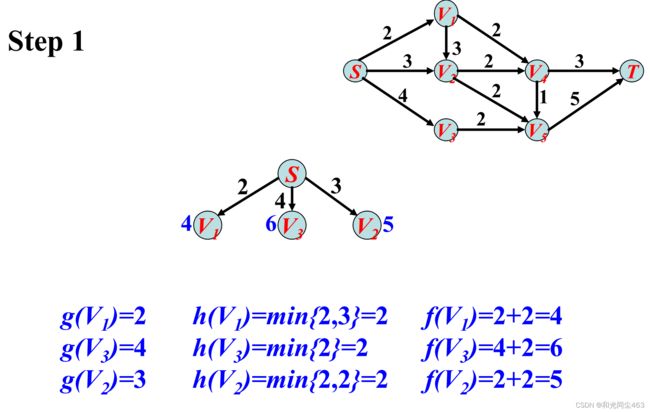
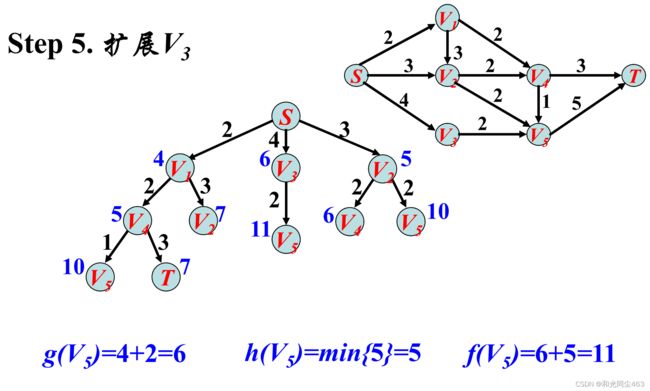
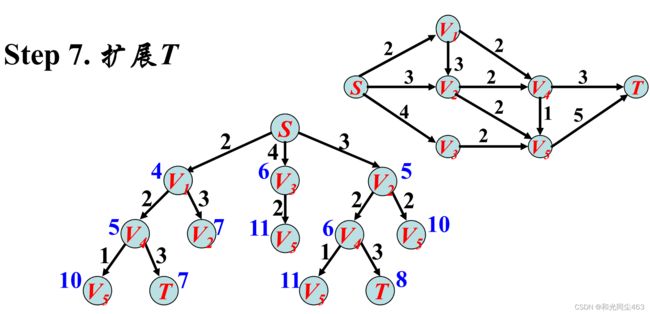
利用A*算法求S到T的最短举例 并写出具体过程

 

题思路很简单没什么说的 f = g+h 但是在我做题的过程中看到这样几个问题,第一,绿色笔部分,不是从S看到拓展点的距离,刚开始的g只和他的父亲 有关 就是说他的父亲决定了他之前走的路径

     这个题 运用了类似于best first的策略和方法,数据结构使用了堆这个数据结构 可以在全局中选择当前最优化的选择 删除和选择过程中运用了堆的调整,读者可以自行复习堆相关的插入删除知识点

     当得到一个可行解 是否继续将小于下界的节点进行扩展 保留争议 有待商榷