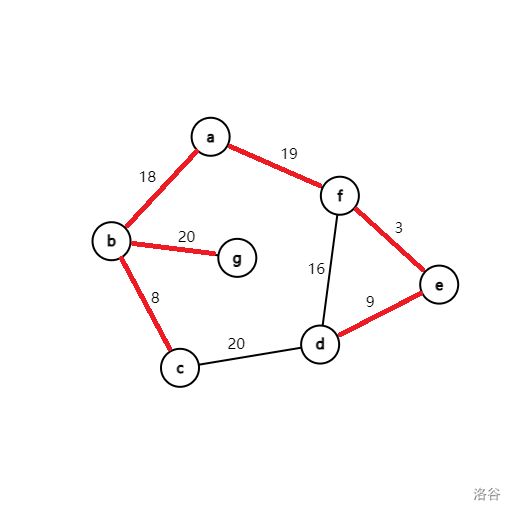
Prim算法求最小生成树

什么是图的最小生成树

一个有 $N$ 个点的图，边一定是大于等于 $N-1$ 条的。图的最小生成树，就是在这些边中选择 $N-1$ 出来，连接所有的 $N$ 个点。这 $N-1$ 条边的边权之和是所有方案中最小的。

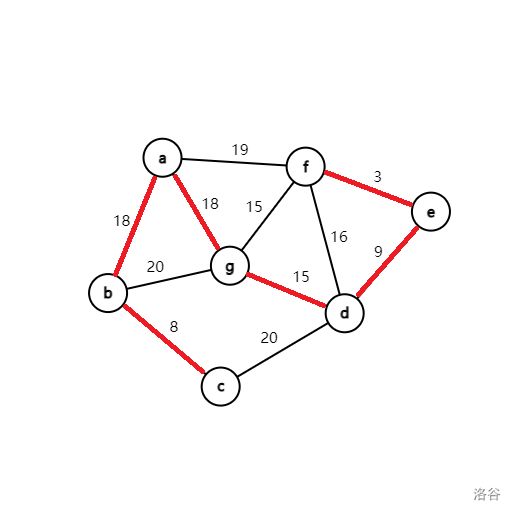
如图，该最小生成树的权值为 $8+18+18+15+9+3=71$。

常用算法

Prim 算法

Prim 算法采用与 Djikstra、Bellman-Ford 算法一样的“蓝白点”思想：白点代表已经进入最小生成树的点，蓝点代表未进入最小生成树的点。

以 1 为起点生成最小生成树，min[v] 表示蓝点 v 与白点相连的最小边权，$\mathrm{MST}$ 表示最小生成树的边权之和。

• 初始化：min[v] $=\infty$ ，min[1] $=0$，$\mathrm{MST}=0$。

• for(int i=1;i<=n;i++)

1. 寻找 min[u] 最小的蓝点 u。

2. 将 u 标记为白点。

3. $\mathrm{MST} $ += min[u]。

4. for 循环寻找与白点 u 相连的所有蓝点 v，并将 min[v] 更新。

if(w[u][v]<min[v])
	min[v]=w[u][v];

5. 求得 $\mathrm{MST}$ 即为最小生成树的权值之和。

算法图解

dis
a	$0$
b	$\infty$
c	$\infty$
d	$\infty$
e	$\infty$
f	$\infty$
g	$\infty$

初始时，所有的点都是蓝点，dis[1]=0，其余均为 $\infty$，$\mathrm{MST}=0$。

---

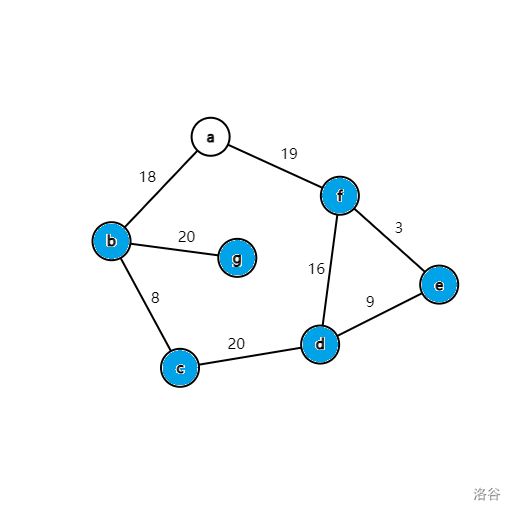
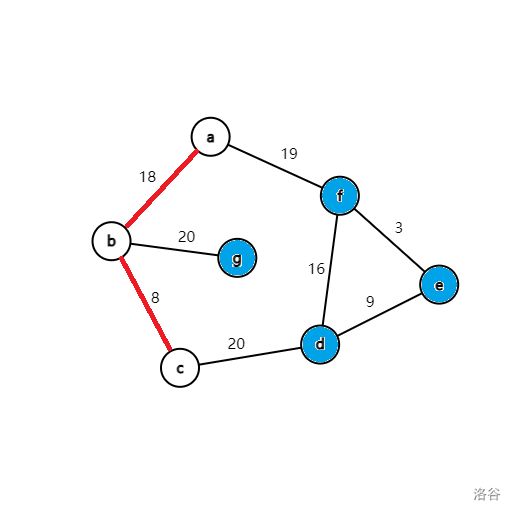
第一轮循环找到 dis[a] 最小，将蓝点 a 变为白点，然后循环枚举所有与 a 相连的所有蓝点 b、f，修改它们与白点相连边权的最小值。

dis
a	$0$
b	$18$
c	$\infty$
d	$\infty$
e	$\infty$
f	$19$
g	$\infty$

---

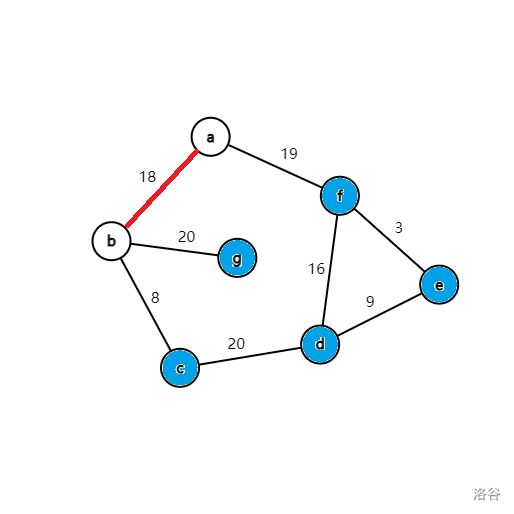
再进行第二轮循环，从蓝点中找到 dis[b] 最小，将 b 变为白点，然后循环枚举所有与 b 相连的所有蓝点 g、c，修改它们与白点相连边权的最小值。

dis
a	$0$
b	$18$
c	$8$
d	$\infty$
e	$\infty$
f	$19$
g	$20$

---

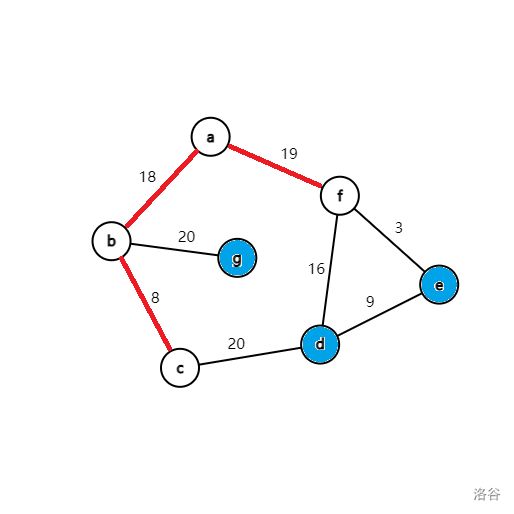
再进行第三轮循环，从蓝点中找到 dis[c] 最小，将 c 变为白点，然后循环枚举所有与 c 相连的蓝点 d，修改它与白点相连边权的最小值。

dis
a	$0$
b	$18$
c	$8$
d	$20$
e	$\infty$
f	$19$
g	$20$

---

再进行第四轮循环，从蓝点中找到 dis[f] 最小，将 f 变为白点，然后循环枚举所有与 d 相连的蓝点 e，修改它与白点相连边权的最小值。

dis
a	$0$
b	$18$
c	$8$
d	$16$
e	$3$
f	$19$
g	$20$

（d 点的 dis[d] 有更小值，将 20 更新为 16）

---

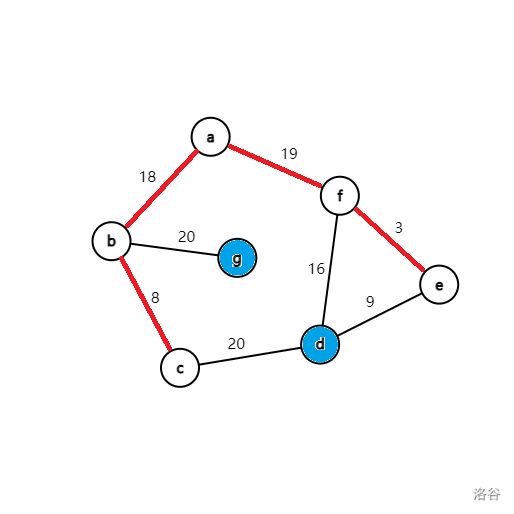
再进行第五轮循环，从蓝点中找到 dis[e] 最小，将 e 变为白点，然后循环枚举所有与 e 相连的蓝点 d，修改它与白点相连边权的最小值。

dis
a	$0$
b	$18$
c	$8$
d	$9$
e	$3$
f	$19$
g	$20$

（d 点的 dis[d] 有更小值，将 16 更新为 9）

---

再进行第六轮循环，从蓝点中找到 dis[e] 最小，将 e 变为白点，但是没有任何的蓝点与其相连，故不进行更新。

dis
a	$0$
b	$18$
c	$8$
d	$9$
e	$3$
f	$19$
g	$20$

---

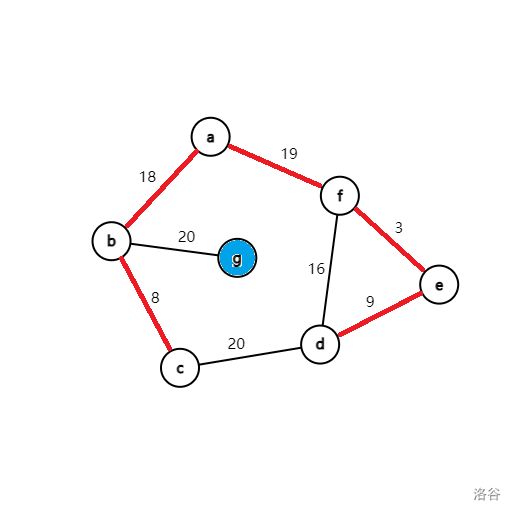
最后，只有 g 为蓝点，将 g 变为白点。

最终，权值之和 $MST=8+18+19+3+9+20=77$

---

例题：洛谷 P3366 【模板】最小生成树

标程：

#include
#include
#include
#include
#define ull unsigned long long
#define ll long long
#define N 200005
#define INF 0x3f3f3f3f
using namespace std;
int head[N],num_edge;
int dis[N];
bool vis[N];
struct Edge{
	int nxt,to,dis;
}edge[2*N];
void add(int from,int to,int dis){
	num_edge++;
	edge[num_edge].nxt=head[from];
	edge[num_edge].to=to;
	edge[num_edge].dis=dis;
	head[from]=num_edge;
}
int cnt,n,m,tot,now=1,ans;
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);//双向加边 
		add(v,u,w);
	}
	for(int i=2;i<=n;i++)
		dis[i]=INF;
	for(int i=head[1];i;i=edge[i].nxt){
		dis[edge[i].to]=min(dis[edge[i].to],edge[i].dis);
	}
	for(int i=1;i<=n-1;i++){
		if(tot>=n-1)
			break;
		int minn=INF;
		vis[now]=1;
		for(int j=1;j<=n;j++){//枚举每一个没有使用的点,找出最小值作为新边
			if(vis[j]==0 && minn>dis[j]){
				minn=dis[j];
				now=j;
			}
		}
		if(vis[now]){
			puts("orz");
			return 0;
		}
		ans+=minn;
		for(int j=head[now];j;j=edge[j].nxt){//枚举now的所有连边，更新dist数组
			int v=edge[j].to;
			if(dis[v]>edge[j].dis && vis[v]==0){
				dis[v]=edge[j].dis;
			} 
		}
		tot++;
	}
	if(tot==n-1)
		cout<<ans<<endl;
	else
		cout<<"orz"<<endl;
	return 0;
}