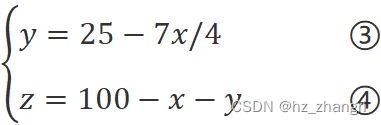常用算法——枚举算法

    在进行归纳推理时，如果逐个考察了某类事件的所有可能情况，因而得出一般结论，那么这结论是可靠的，这种归纳方法叫做枚举算法

一、基本概念和算法

    枚举算法简称枚举法，也称为列举法、穷举法，是暴力策略的具体体现，又称为蛮力法。

    枚举法的基本思想是：逐一列举问题所涉及的所有情形，并根据问题提出的条件检验哪些是问题的解，哪些应予排除。

• 枚举的意义

1) 可以充分利用计算机的速度，解决一些常见问题

2) 如果问题的规模不大，使用枚举，运算速度是可以接收的。

3) 枚举可作为某类问题时间性能的底线，用来引出同样问题的更高效率的算法。

• 枚举的实施步骤(算法)

1) 根据问题的具体情况确定枚举量(简单变量或数组)

2) 根据问题的具体清空确定枚举范围，设置枚举循环

3) 根据问题的具体要求确定筛选(约束)条件

4) 设计枚举程序并运行、调试，对运行结果进行分析与讨论。

二、判断阿姆斯特朗数

    例1 求三到十位的“阿姆斯特朗数”。

    所谓“阿姆斯特朗数”是指一个三位数及以上的数，其各位数字的位数次方和等于其本身。例如：153是一个阿姆斯特朗数，因为

    。

    472335975是一个阿姆斯特朗数，因为

   

    其中不同位数的阿姆斯特朗数也有别名，如三位的阿姆斯特朗数也叫“水仙花数”，七位的阿姆斯特朗数也叫“北斗七星数”等。

    那么这道题的取值范围即100-10000000000(，不含)，条件限制为各位数字的位数次方和等于其本身。

    如何取各位数字？

    可用整除、取余获取各位数字，但位数不定不好处理，故可以转化为字符串，求长度(次方数)，取字符串元数(每一位数)。

    数值转为字符串的语法格式为：

str(数值表达式)

    转换后，正数不含符号位，字符串为序列，每个字符为元素。

    f格式化字符串：f-string采用{content:format}设置字符串格式，其中content是替换并填入字符串的内容，可以是变量、表达式或函数等，format是格式描述符。采用默认格式时不必指定 “:format”。其语法格式为：

f'{字符串/变量:格式}'

其中：大括号前、后：可以放任何字符串，它们将直接显示在结果中；大括号内：目标字符串+目标格式；冒号前：需要格式化的原始字符串或变量，冒号后：需要的目标格式(缺省用默认格式)

完整程序如下：

for i in range(100,10**10):  # 不含10**10，终值为9999999999
    s = 0                # 求和初值取“0”
    n = len(str(i))      # 获取数值i的位数
    for j in str(i):     # str(123)='123'，则j='1','2','3'
        s += int(j) ** n # 求各位数的n次方和
    if s == i:           # n位阿姆斯特朗数的判断条件
        print(f'{n}位阿姆斯特朗数:', i)

执行结果：

    此程序虽然简单，但输出效果不是很理想，同样位数的阿姆斯特朗数没有显示在同一行中。此程序涉及100亿次的10位100亿次方数和运算，所以会耗费数小时(7位前耗时数秒，8位前耗时1~2分，9位前耗时数10~30分)

    下面对程序进行改进，将不同位数的阿姆斯特朗数标上“别名”，并将相同位数的阿姆斯特朗数显示在同一行中，但耗时基本不变。下面的程序中用到了三元表达式。

    三元表达式又称三元运算符，Python中三元表达式的语法格式为：

表达式1 if 条件表达式 else 表达式2

    当“条件表达式”为True时，返回结果为“表达式1”，否则返回结果为“表达式2”。

    获取字典“键”的列表的语法格式为：

list(字典.keys())

    完整程序如下：

ArmstrongNum = {'三':'水仙花','四':'四叶玫瑰','五':'五角星','六':'六合',
            '七':'北斗七星','八':'八仙','九':'九九重阳','十':'十全十美'}
for i in range(2,10):
    print(f'{list(ArmstrongNum.keys())[i-2]}位的'
          f'{ArmstrongNum[list(ArmstrongNum.keys())[i-2]]}数：', end='')
    m = 0
    for j in range(10**i, 10**(i+1)):	# 1后跟i个0到 i+1个9
        n = len(str(j))					# n = i + 1，数值j的位数
        s = 0
        for k in str(j):				# str(123)='123'，k='1','2','3'
            s += int(k) ** n			# 求各位的n次方和
        if s == j:						# n位阿姆斯特朗数的判断条件
            print(j if m==0 else f', {j}', end='')
            m += 1
    print()

执行结果：

三、解百鸡问题

    我国古代数学家张丘建在《算经》一书中提出的数学问题：鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一。百钱买百鸡，问鸡翁、鸡母、鸡雏各几何？

    例2 百鸡问题：(白话文翻译)有一个人有一百个钱，打算买一百只鸡。到市场一看，公鸡五个钱一只，母鸡三个钱一只，小鸡一个钱三只，怎么样买法，才能刚好用一百个钱买一百只鸡？。现在，请你编一程序，帮他计划一下。

    注意：鸡都是整只的，钱总数也是整数。因为买公鸡和母鸡花费的钱为整数，所以买小鸡的钱也必须是整数，因此小鸡数为3的倍数。

    设公鸡数为rooster，母鸡数为hen，则小鸡数为

chicken = 100-rooster-hen

    一百个钱最多买20只公鸡，一百个钱最多买33只母鸡。具体程序代码如下：

for rooster in range(21):			# 公鸡0~20，不包含21
    for hen in range(34):			# 母鸡0~33，不包含34
        chicken = 100-rooster-hen	# 求小鸡数
        if rooster * 5 + hen * 3 + chicken/3 == 100:
            print(f'公鸡{rooster}只+母鸡{hen}只+小鸡{chicken}只=100只鸡。')

输出结果为：

 

程序优化：

    思路：设公鸡数为x，母鸡数为y，小鸡数为z，则

    

    两方程三变量，不能直接求解，属不定方程。

    程序每使用一个for(x)循环，就相当于将一个未知数(x)变成已知数(x), 两个方程两个未知数，方程就具有可解性了，这样就可以， 继续减少一个循环的嵌套。则解方程①②得

    

可用一个循环求解问题。

for x in range(21):							# 0~20，不包含21。公鸡数不会超过20
    y = int(25-7*x/4) if 25 >= 7*x/4 else 0	# 先求y(母鸡数为整数且大于等于0)
    z = 100-x-y								# 再求z
    if x * 5 + y * 3 + z / 3 == 100:
        print(f'公鸡{x}只+母鸡{y}只+小鸡{z}只=100只鸡。')

输出结果为：