深度学习之基础知识详解(文末有福利)
过拟合,欠拟合
过拟合(overfitting):学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了。
欠拟合(underfitting):学习能太差,训练样本的一般性质尚未学好。
下面是直观解释:
 《机器学习》--周志华
《机器学习》--周志华
下面在那一个具体的例子: 如果我们有6个数据,我们选择用怎么样的回归曲线对它拟合呢?看下图

在这里我们可以发现,原来过拟合和欠拟合和模型复杂度是相关的,具体描述如下图
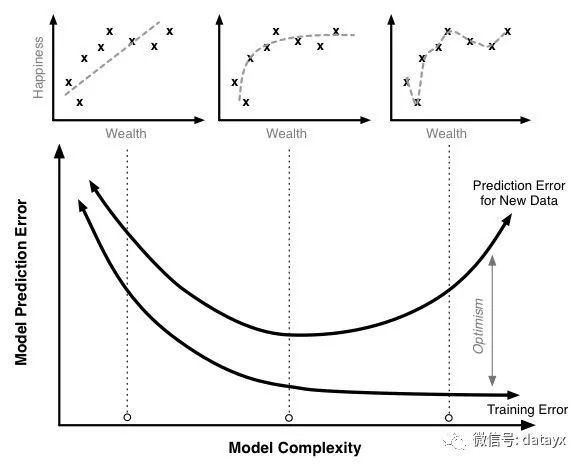
也就是说,在模型相对复杂时,更容易发生过拟合,当模型过于简单时,更容易发生欠拟合。
当然,为了防止过拟合,也会有 cross validation,正则化等等方法
正则化
正则化的主要目的是为了防止过拟合,而它的本质是约束(限制)要优化的参数。通常我们通过在Cost function误差函数中添加惩罚项来实现正则化。当然,正则化有其缺点,那就是引入正则化可能会引起“too much regularization”而产生误差。
问:对于正则化,有使模型“简单”的优点,这其中”简单”怎么理解?
答:引用李航老师书中的那段话:正则化符合奥卡姆剃刀 (Occam’s razor)原理。奥卡姆剃刀原理应用于模型选择时变为以下想法:在所有可能选择的模型中,能够很好地解释已知数据并且十分简单才是最好的模型,也就是应 该选择的模型。从贝叶斯估计的角度来看,正则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率,简单的模型有较小的先验概率。
需要注意的是,在正则化的时候,bais是不需要正则化的,不然可能会导致欠拟合!
下面介绍一些常见的正则化方式:
L1,L2的图像化:


L2 针对于这种变动, 白点的移动不会太大, 而 L1的白点则可能跳到许多不同的地方 , 因为这些地方的总误差都是差不多的. 侧面说明了 L1 解的不稳定性。
注意记住:L1正则化会让权重向量在最优化的过程中变得稀疏(即非常接近0),使得L1很多时候也拿来做特征选择;L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚,倾向于更加分散的权重向量。
 来自论文
来自论文
Dropout可以看作是Bagging的极限形式,每个模型都在当一种情况中训练,同时模型的每个参数都经过与其他模型共享参数,从而高度正则化。在训练过程中,随机失活也可以被认为是对完整的神经网络抽样出一些子集,每次基于输入数据只更新子网络的参数(然而,数量巨大的子网络们并不是相互独立的,因为它们都共享参数)。在测试过程中不使用随机失活,可以理解为是对数量巨大的子网络们做了模型集成(model ensemble),以此来计算出一个平均的预测。
关于Dropout的Motivation:一个是类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。还有一个就是正则化的思想,减少神经元之间复杂的共适应关系,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
这里强烈推荐看下论文原文。虽然是英文的,但是对于更深刻的理解还是有很大帮助的!https://link.zhihu.com/?target=http%3A//www.cs.toronto.edu/%7Ersalakhu/papers/srivastava14a.pdf
图像数据的预处理
为什么要预处理:

下面介绍下一些基础预处理方法:
归一化处理
-
均值减法(Mean subtraction):它对数据中每个独立特征减去平均值,从几何上可以理解为在每个维度上都将数据云的中心都迁移到原点。(就是每个特征数据减去其相应特征的平均值)
归一化(Normalization);先对数据做零中心化(zero-centered)处理,然后每个维度都除以其标准差。
 (中间零中心化,右边归一化)
(中间零中心化,右边归一化)
PCA和白化(Whitening)
-
白化(Whitening):白化操作的输入是特征基准上的数据,然后对每个维度除以其特征值来对数值范围进行归一化。该变换的几何解释是:如果数据服从多变量的高斯分布,那么经过白化后,数据的分布将会是一个均值为零,且协方差相等的矩阵
特征向量是按照特征值的大小排列的。我们可以利用这个性质来对数据降维,只要使用前面的小部分特征向量,丢弃掉那些包含的数据没有方差的维度。 这个操作也被称为主成分分析( Principal Component Analysis)简称PCA)降维
 (中间是经过PCA操作的数据,右边是白化)
(中间是经过PCA操作的数据,右边是白化)
需要注意的是:
对比与上面的中心化,与pca有点类似,但是不同的是,pca把数据变换到了数据协方差矩阵的基准轴上(协方差矩阵变成对角阵),也就是说他是轴对称的,但简单的零中心化,它不是轴对称的;还有PCA是一种降维的预处理,而零中心化并不是。
常见错误:任何预处理策略(比如数据均值)都只能在训练集数据上进行计算,算法训练完毕后再应用到验证集或者测试集上。例如,如果先计算整个数据集图像的平均值然后每张图片都减去平均值,最后将整个数据集分成训练/验证/测试集,那么这个做法是错误的。应该怎么做呢?应该先分成训练/验证/测试集,只是从训练集中求图片平均值,然后各个集(训练/验证/测试集)中的图像再减去这个平均值。
Batch Normalization
原论文中,作者为了计算的稳定性,加了两个参数将数据又还原回去了,这两个参数也是需要训练的。说白了,就是对每一层的数据都预处理一次。方便直观感受,上张图:
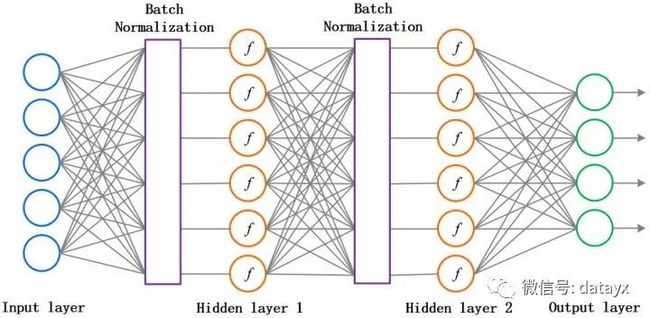
这个方法可以进一步加速收敛,因此学习率可以适当增大,加快训练速度;过拟合现象可以得倒一定程度的缓解,所以可以不用Dropout或用较低的Dropout,而且可以减小L2正则化系数,训练速度又再一次得到了提升。即Batch Normalization可以降低我们对正则化的依赖程度。
还有要注意的是,Batch Normalization和pca加白化有点类似,结果都是可以零均值加上单位方差,可以使得数据弱相关,但是在深度神经网络中,我们一般不要pca加白化,原因就是白化需要计算整个训练集的协方差矩阵、求逆等操作,计算量很大,此外,反向传播时,白化操作不一定可导 。最后,再次强烈直接看BN的相关论文,有很多细节值得一看!
https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1502.03167v3
神经元
下面图表的左边展示了一个生物学的神经元,右边展示了一个常用的数学模型。乍一看还是有点相似的,事实上也是,人工神经网络中的神经元也有受到生物神经元的启发。总结要点:
在生物的神经元(也就是左图)中,树突将信号传递到细胞体,信号在细胞体中相加。如果最终之和高于某个阈值,那么神经元将会激活,向其轴突输出一个峰值信号,注意这里输出是一个脉冲信号!
在数学计算模型(也就是右图)中,首先将输入进行加权求和加上偏执,得到待激励值,然后将该值作为输入,输入到激活函数中,最后输出的是一个激励后的值,这里的激活函数可以看成对生物中神经元的激活率建模。由于历史原因,激活函数常常选择使用sigmoid函数 ,当然还有很多其他激活函数,下面再仔细聊!
需要注意:1.一个神经元可以看成包含两个部分,一个是对输入的加权求和加上偏置,一个是激活函数对求和后的激活或者抑制。2.注意生物中的神经元要复杂的多,其中一个是生物中的输出是一个脉冲,而现在大多数的数学模型神经输出的就是一个值,当然现在也有一些脉冲人工神经网络,可以自行了解!

作为线性分类器的单个神经元
比如基础的逻辑回归,结合上面的神经元知识,可以发现,逻辑回归就是激活函数是sigmoid的单层简单神经网络。也就是说,只要在神经元的输出端有一个合适的损失函数,就能让单个神经元变成一个线性分类器。因此说,那些线性的分类器本身就是一个单层神经网络
但注意,对于非线性的模型:SVM和神经网络走了两条不同的道路:神经网络通过多个隐层的方法来实现非线性的函数,有一些理论支持(比如说带隐层的神经网络可以模拟任何函数),但是目前而言还不是非常完备;SVM则采用了kernel trick的方法,这个在理论上面比较完备(RKHS,简单地说就是一个泛函的线性空间)。两者各有好坏,神经网络最近的好处是网络设计可以很灵活,有很多的trick&tip,很多理论都不清不楚的;SVM的理论的确漂亮,但是kernel设计不是那么容易,所以最近也就没有那么热了。
为什么要是深度神经网而不是”肥胖“(宽度)神经网络?

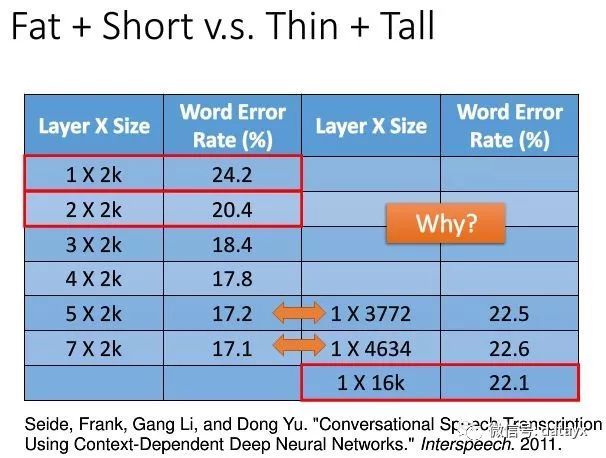
“肥胖”网络的隐藏层数较少,如上左图。虽然有研究表明,浅而肥的网络也可以拟合任何的函数,但它需要非常的“肥胖”,可能一层就要成千上万个神经元。而这直接导致的后果是参数的数量增加到很多很多。
也有实验表明,也就是上图的实验,我们可以清楚的看出,当准确率差不多的时候,参数的数量却相差数倍。这也说明我们一般用深层的神经网络而不是浅层“肥胖”的网络。
注意:说神经网络多少层数的时候一般 不包括输入层。 在神经网络中的激活主要讲的是梯度的更新的激活
为什么在人工神经网络中的神经元需要激活函数?

上图可看做普通的线性分类器,也就是线性回归方程。这个比较基础,效果如右图。当然有时候我们发现这样的线性分类器不符合我们要求时,我们很自然的想到那我们就加多一层,这样可以拟合更加复杂的函数,如下图a:
 图a
图a  图b
图b
但同时当我们动笔算下, 就会发现, 这样一个神经网络组合起来,输出的时候无论如何都还是一个线性方程。如上图b右边,就只能这样分类。(那也太蠢了吧)。下图表示一层加如激活函数的情况!

一层很多时候是远远不够的,前面讲过,简单的线性分类器就可以看成是一层的神经网络,比如上图,激活函数是signmoid,那就可以看成是二分类的逻辑回归!
下面扩展到多层,如下图1,2:
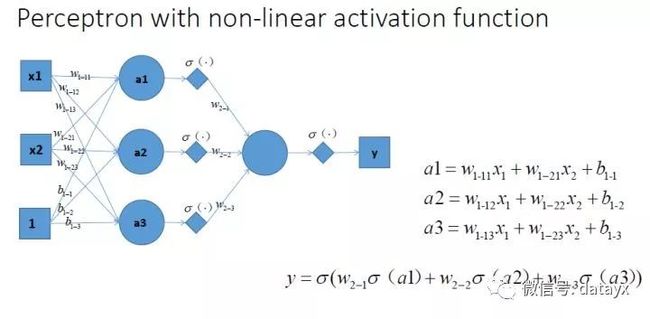 图1
图1  图2
图2
图1是一个简单的MLP(全链接神经网络),图2的右边课简单表示左图的可视化,那么对比之前的无激活函数的图,很明显是更加的非线性,拟合能力也会更强,同时可以想到,当层数更多,其能力也会越来越强!
简单来说:就是使得神经网络具有的拟合非线性函数的能力,使得其具有强大的表达能力!
简单扩展,神经网络的万能近似定理:一个前馈神经网络如果具有线性层和至少一层具有"挤压"性质的激活函数(如signmoid等),给定网络足够数量的隐藏单元,它可以以任意精度来近似任何从一个有限维空间到另一个有限维空间的borel可测函数。
要相符上面的定理,也就是想拟合任意函数,一个必须点是“要有带有“挤压”性质的激活函数”。这里的“挤压”性质是因为早期对神经网络的研究用的是sigmoid类函数,所以对其数学性质的研究也主要基于这一类性质:将输入数值范围挤压到一定的输出数值范围。(后来发现,其他性质的激活函数也可以使得网络具有普适近似器的性质,如ReLU 。
一些主要的激活函数
sigmoid
优点:有较好的解释性
缺点:1.Sigmoid函数饱和使梯度消失。sigmoid神经元有一个不好的特性,就是当神经元的激活在接近0或1处时会饱和:在这些区域,梯度几乎为0。2.输出不是零中心的,这一情况将影响梯度下降的运作,因为如果输入神经元的数据总是正数,那么关于w的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数,这样梯度下降权重更新时出现z字型的下降。这样收敛会变得异常的慢。(这也是为什么要一直保持为数据的0中心化)—–但这个问题比较小3.exp()在深度神经网络时候相比其他运算就比较慢

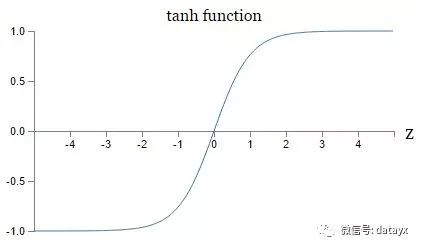
Tanh非线性函数
优点:1.它的输出是零中心的。因此,在实际操作中,tanh非线性函数比sigmoid非线性函数更受欢迎。
缺点:1.和Sigmoid函数一样,饱和使梯度消失。计算慢
ReLU
优点:1.ReLU对于随机梯度下降的收敛有巨大的加速作用( Krizhevsky 等的论文alexnet指出有6倍之多)。据称这是由它的线性,非饱和的公式导致的;2.注意:现在大部分的DNN用的激活函数就是ReLu
缺点:1.当x是小于0的时候,那么从此所以流过这个神经元的梯度将都变成0;这个时候这个ReLU单元在训练中将死亡(也就是参数无法更新),这也导致了数据多样化的丢失(因为数据一旦使得梯度为0,也就说明这些数据已不起作用)。

Leaky ReLU
优点:1.非饱和的公式;2.Leaky ReLU是为解决“ReLU死亡”问题的尝试
缺点:1.有些研究者的论文指出这个激活函数表现很不错,但是其效果并不是很稳定
Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU,把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。

ELU
指数线性单元(Exponential Linear Units, ELU) ELU的公式为:

ELU.png 函数曲线如下:

Maxout
Maxout是对ReLU和leaky ReLU的一般化归纳
优点:1.拥有ReLU单元的所有优点(线性操作和不饱和),而没有它的缺点(死亡的ReLU单元)
缺点 :1.每个神经元的参数数量增加了一倍,这就导致整体参数的数量激增。难训练,容易过拟合
怎么用激活函数
“那么该用那种呢?”用ReLU非线性函数。注意设置好学习率,(如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。),解决方案:或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid了。也可以试试tanh,但是其效果应该不如ReLU或者Maxout。
神经网络中的偏置有什么意义?
最基础的神经元感知器如下:
初始化神经网络的参数可以全为0吗,其他普通线性分类器呢?
我们前面说过:线性分类器逻辑回归模型可以算作为一个简单的单层神经网络。为了更好的说明问题,假设一个场景,在十类分类的数字手写识别中,我们将本来二分类的逻辑回归推到多分类的softmax,也就是说,神经元的激活函数是softmax。也就是下图,然后分析:
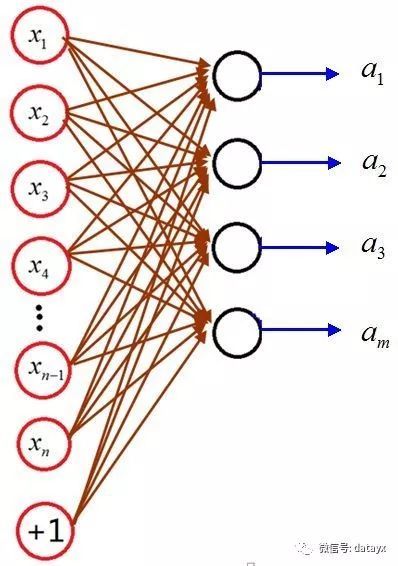
得出结论,没有隐层时, 可以将所有的参数初始化为0.
如果有隐层呢?假如还是用sigmoid激活函数呢。来个更简单MLP,

对于隐层使用了其他函数比如ReLU: f(net)=max(0,net)其结果也是一样的: 除了输入层的输出值为x本身, 不为0, 其余的所有层的输出都为0. BP时所有梯度也都为0, 包括输出层. 这意味着所有的非输入神经元都是无意义的. 学习失败.对于卷积神经网络,循环神经网络也是一样的,故一般会用其他初始化方式。
最后最后的结论是, 一般只在训练SLP/逻辑回归模型时才使用0初始化所有参数., 更实用的结论是, 深度模型都不会使用0初始化所有参数.
交叉熵存在的意义和与平方差相比有什么好处?
一个非常常见的,非常漂亮的成本函数是“交叉熵”(cross-entropy)。交叉熵产生于信息论里面的信息压缩编码技术,但是它后来演变成为从博弈论到机器学习等其他领域里的重要技术手段。它的定义如下:
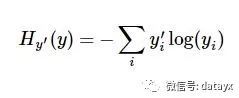
其中,y 是我们预测的概率分布, y’ 是实际的分布
1.交叉熵是正的,2.当所有输入x的输出都能接近期望输出y的话,交叉熵的值将会接近 0。这两个特征在直觉上我们都会觉得它适合做代价函数。事实上,我们的均方代价函数也同时满足这两个特征。然而....
为什么在神经网络中用交叉熵代替二次代价函数?
还是从反向传播,参数更新的角度理解更新参数的公式如下:

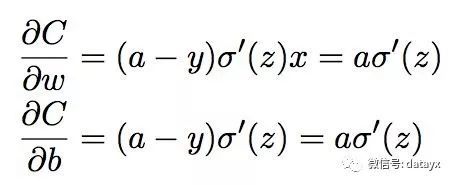
a 是 神经元的输出,其中 a = σ(z), z = wx + b,可知,偏导数受激活函数的导数影响,假设这里是传统的sigmoid激活函数(在之前很多时候都是)。那么sigmoid 的导数在输出接近 0 和 1 的时候 是非常小的,这会导致一些实例在刚开始训练时学习得非常慢!
但是如果换成是交叉熵loss,其更新权重公式最后推导得出如下:
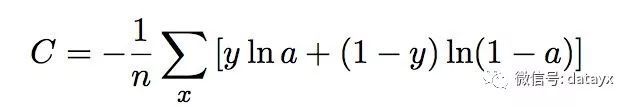

由以上公式可知,权重学习的速度受到 σ(z) − y 影响,更大的误差,就有更快的学习速度,还避免了二次代价函数方程中因 σ′(z) 导致的学习缓慢。
但是现在也有很多其他的激活函数并不会产生饱和状态,那么均方差也有其存在价值。
福利时间
关注本公众号:人工智能与大数据生活(data_cricle), 数据真人送您
2.7G 380份最新数据分析报告
40G 人工智能算法课
已关注的小伙伴,直接回复数据分析报告、人工智能算法
后台回复 PM2.5 获得 Python分析北京pm2.5 源代码以及数据集
原文链接: Python分析北京PM2.5,原来每年的值都在变少......
后台回复 世界杯, 获得 预测世界杯冠军源代码以及数据集
原文链接:2018世界杯来了,利用Python预测冠军(附全部代码和数据集)
后台回复 美国劳工部,获得完整报告
感谢您的阅读,祝您一天好心情!
长按二维码,关注我们
![]()









