数据结构之二叉树练习

1.二叉树的结构

• 二叉链表结构：

struct BiNode{
	char data;
	BiNode* lChild;
	BiNode* rChild;
	BiNode():lChild(NULL),rChild(NULL){}
}

• 三叉链表结构

struct BiNode{
	char data;
	BiNode* lChild;
	BiNode* rChild;
	BiNode* father;
	BiNode():lChild(NULL),rChild(NULL),father(NULL){}
}

2.二叉树的创建

• 给出先序遍历的字符串，空树用 ‘#’ 表示(有些用‘0’)，根据给出的先序遍历结果创建二叉树。

样例输入：AB#C##D##

• 二叉链表代码：

void CreateBiTree(BiNode* &T){
	char ch;
	cin >> ch;
	if(ch == '#'){
		T = NULL;
	}else{
		T = new BiNode();
		T->data = ch;
		CreateBiTree(T->lChild);
		CreateBiTree(T->rChild);
	}
}

这里函数参数中的&号是必需的，因为我们需要改变传入的指针自身的值。否则无法成功创建树。

• 三叉链表代码：

BiNode* CreateBiTree(BiNode* T){
	BiNode* p;
	char ch;
	cin >> ch;
	if(ch == '#'){
		p = NULL;
	}else{
		p = new BiNode();
		p->data = ch;
		p->father = T;
		p->lChild = CreateBiTree(p);
		p->rChild = CreateBiTree(p);
	}
	return p;
}

注意在主函数中要用根结点指针去接收函数最后返回的值。即T = CreateBiTree(T);

3.二叉树的遍历

• 这里主要展示后序遍历非递归的代码，因为三种遍历方式的递归程序和先序遍历、中序遍历的非递归程序很好理解，自己多看代码即可。

void PostOrderTraverse(BiNode* T){
    int tag = 0;
    stack<BiNode *> s1;
    stack<int> s2; //(1)
    BiNode *p = T;
 
    do{
        if(p){
            s1.push(p);
            tag = 0;
            s2.push(tag);
            p = p->lChild;
        }else{
            if(s2.top() == 0){
                tag = 1;
                s2.top() = tag;
                p = s1.top()->rChild; //(2)
            }else{
                p = s1.top();
                s1.pop();
                s2.pop();
                cout << p->data;
                p = NULL; //(3)
            }
        }
    } while (!s1.empty());
}

这里有三点需要注意：
(1) 每次遍历根结点先进栈，但是在访问完左子树和右子树时当前指针p都是空的。访问完左子树时根结点还不能出栈，只有当右子树访问完毕后，根结点才能出栈并输出其数据。因此这里使用了另外一个状态栈，通过0和1标志当前访问完的是左子树还是右子树，决定根结点是否需要出栈。
(2) 由于当前p是空的，因此需要用栈顶元素来访问右子树，即s1.top()。
(3) 在访问完根结点的左右子树和它本身之后，程序需要回到当前根结点的父节点去继续往后访问。因此要在这里把p置空。

4.求二叉树的叶子数目

• 叶子指的是没有孩子的结点。这里采用递归的方法去查找。

int countLeaves(BiNode* T){
    if(T && T->lChild == NULL && T->rChild == NULL){
        return 1;
    }else if(T){
        int left = countLeaves(T->lChild);
        int right = countLeaves(T->rChild);
        return left + right;
    }
    return 0;
}

在思考时要注意叶子结点的特点：当前结点不为空，左右孩子结点都为空。 如果当前结点不空，而且至少有一个孩子不空时，说明它不是叶子结点，要继续往下判断；而当前结点为空时，程序不能再往下了，这里返回0即可。这里将左右子树寻找的结果加起来，即可得到最终的结果。

5.求二叉树的高度

int getHeight(BiNode* T){
	if(T){
		int left = getHeight(T->lChild);
		int right = getHeight(T->rChild);
		if(left > right){
			return left + 1;
		}else{
			return right + 1;
		}
	}else{
		return 0;
	}
}

算法思路：求二叉树的高度是找到从根结点到叶子结点路径最长的一条。我们可以先一路走到底，即找到叶子结点的孩子(空节点)，然后一步步返回，每返回一层就在原来的基础上加1记录层数，同时每返回到一个结点时比较它左右子树的层数，取大的值再继续往上返回。这里就相当于从下往上计算高度了。

6.应用（例题分析）

例1：DS二叉树——二叉树之数组存储

题目描述：
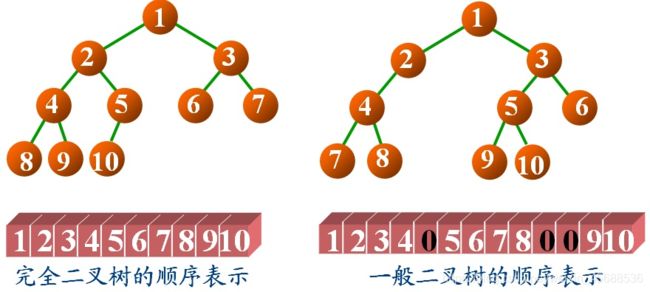
二叉树可以采用数组的方法进行存储，把数组中的数据依次自上而下,自左至右存储到二叉树结点中，一般二叉树与完全二叉树对比，比完全二叉树缺少的结点就在数组中用0来表示。，如下图所示

从上图可以看出，右边的是一颗普通的二叉树，当它与左边的完全二叉树对比，发现它比完全二叉树少了第5号结点，所以在数组中用0表示，同样它还少了完全二叉树中的第10、11号结点，所以在数组中也用0表示。
结点存储的数据均为非负整数

输入：
第一行输入一个整数t，表示有t个二叉树
第二行起，每行输入一个数组，先输入数组长度，再输入数组内数据，每个数据之间用空格隔开，输入的数据都是非负整数
连续输入t行

输出：
每行输出一个示例的先序遍历结果，每个结点之间用空格隔开

样例输入：
3
3 1 2 3
5 1 2 3 0 4
13 1 2 3 4 0 5 6 7 8 0 0 9 10

样例输出：
1 2 3
1 2 4 3
1 2 4 7 8 3 5 9 10 6

提示：注意从数组位置和二叉树深度、结点位置进行关联，或者父子结点在数组中的位置存在某种管理，例如i, i+1, i/2, i+1/2……或者2i, 2i+1……

这里只给出创建二叉树、求高度、先序遍历的代码。

void CreateBiTree(BiNode* &T, int* arr, int h, int H, int i, int len){
    if(i > len || h > H){
        T = NULL;
    }else{
        T = new BiNode;
        T->data = arr[i];
        CreateBiTree(T->lChild, arr, h + 1, H, 2 * i, len);
        CreateBiTree(T->rChild, arr, h + 1, H, 2 * i + 1, len);
    }
}

int len, height;
cin >> len;
int *arr = new int[len + 1]; //0号空间不用
for (int i = 1; i <= len; i++){
    cin >> arr[i];
}
for (int i = 1;; i++){//求高度
    if(pow(2, i) - 1 > len){
        height = i;
        break;
    }
}

void PreOrderTraverse(BiNode* T){
    if(T){
        if(T->data){
            cout << T->data <<' ';
        }
        PreOrderTraverse(T->lChild);
        PreOrderTraverse(T->rChild);
    }
}

例2：DS二叉树–左叶子数量

题目描述：
计算一颗二叉树包含的叶子结点数量。
左叶子是指它的左右孩子为空，而且它是父亲的左孩子
提示：可以用三叉链表法，也可以用现有算法对两层结点进行判断。
建树方法采用“先序遍历+空树用0表示”的方法

输入：
第一行输入一个整数t，表示有t个测试数据
第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出：
逐行输出每个二叉树的包含的左叶子数量

样例输入：
3
AB0C00D00
AB00C00
ABCD0000EF000

样例输出：
0
1
2

#include
#include
#include
#include
using namespace std;
 
struct BiNode{
    char data;
    BiNode *lChild;
    BiNode *rChild;
    BiNode():lChild(NULL), rChild(NULL){}
};

void CreateBiTree(BiNode* &T){
    char ch;
    cin >> ch;
    if(ch == '0'){
        T = NULL;
    }else{
        T = new BiNode;
        T->data = ch;
        CreateBiTree(T->lChild);
        CreateBiTree(T->rChild);
    }
}

int findLeaf(BiNode* T, int flag){
    if(T && T->lChild == NULL && T->rChild == NULL && flag == 1){
        return 1;
    }else if(T){
        int left = findLeaf(T->lChild, 1);
        int right = findLeaf(T->rChild, 0);
        return left + right;
    }
    return 0;
}
 
int main(){
    int t;
    cin >> t;
    while(t--){
        BiNode *t;
        CreateBiTree(t);
        cout << findLeaf(t, 0) << endl;
    }
    return 0;
}

这里计算叶子数时，为了判断是否为左子树加了一个标志flag，flag=1表示当前叶子为左叶子。

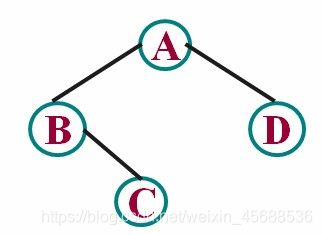
例3：DS二叉树——二叉树之父子结点

题目描述：
给定一颗二叉树的逻辑结构如下图，（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构。编写程序输出该树的所有叶子结点和它们的父亲结点。

输入
第一行输入一个整数t，表示有t个二叉树
第二行起，按照题目表示的输入方法，输入每个二叉树的先序遍历，连续输入t行

输出：
第一行按先序遍历，输出第1个示例的叶子节点
第二行输出第1个示例中与叶子相对应的父亲节点
以此类推输出其它示例的结果

样例输入：
3
AB0C00D00
AB00C00
ABCD0000EF000

样例输出：(每个字符后有空格)
C D
B A
B C
A A
D F
C E

#include
#include
#include
#include
#include
using namespace std;
 
#define N 100
 
int i = 0;
 
struct BiNode{
    char data;
    BiNode *lChild;
    BiNode *rChild;
    BiNode *father;
    BiNode():lChild(NULL), rChild(NULL), father(NULL){}
};

BiNode* CreateBiTree(BiNode* T){
    BiNode *p;
    char ch;
    cin >> ch;
    if(ch == '0'){
        p = NULL;
    }else{
        p = new BiNode;
        p->data = ch;
        p->father = T;
        p->lChild=CreateBiTree(p);
        p->rChild=CreateBiTree(p);
    }
    return p;
}

int findLeaf(BiNode* T, char* child, char* father){
    if(T && T->lChild == NULL && T->rChild == NULL){
        father[i] = T->father->data;
        child[i] = T->data;
        i++;
        return 1;
    }else if(T){
        int left = findLeaf(T->lChild, child, father);
        int right = findLeaf(T->rChild, child, father);
        return left + right;
    }
    return 0;
}

int main(){
    int t;
    cin >> t;
 
    char *child = new char[N];
    char *father = new char[N];
 
    while(t--){
        BiNode *t;
        t = CreateBiTree(t);
 
        i = 0;
        int num = findLeaf(t, child, father);
 
        for (int i = 0; i < num; i++){
            cout << child[i] << ' ';
        }
        cout << endl;
        for (int i = 0; i < num; i++){
            cout << father[i] << ' ';
        }
        cout << endl;
    }
    return 0;
}

这里我使用了一个全局变量的计数器(数组指针)，在找到叶子结点时将叶子和其父结点的数据分别加入数组内存储，并将指针往下。同时对叶子结点进行计数并返回，但是其实可以直接使用全局的计数器 i，意思是一样的，读者可以自己尝试修改。