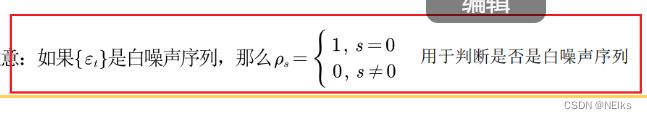数学建模:14 时间序列
目录
步骤
基本概念
时间序列分解
叠加 / 乘积模型
使用SPSS的实例
步骤
指数平滑模型
Simple模型
线性趋势模型
布朗线性趋势模型
阻尼趋势模型
简单季节性
温特加法模型
温特乘法模型
一元时间序列分析的模型
基础概念
平稳时间序列、白噪声序列
差分方程及其特征方程
滞后算子
AR(p)模型(auto regressive) 自回归
特征方程判断平稳性
计算的例子
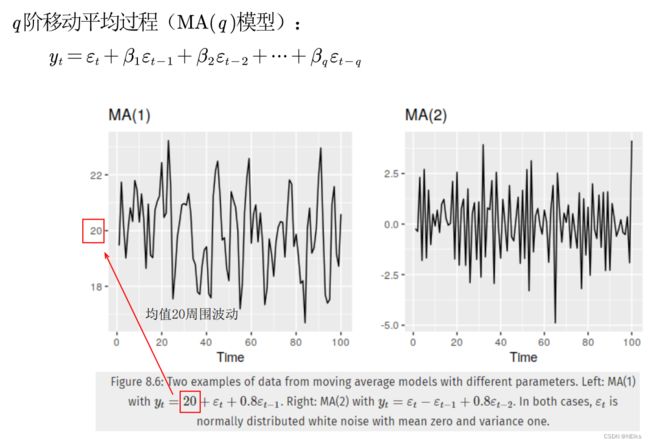
MA(q)模型(moving average)
MA模型和AR模型的关系
ARMA(p,q)模型
选择p、q的方法
ACF自相关系数、PACF偏自相关系数
AIC、BIC准则
检验模型是否识别完全
ARIMA(p,d,q)模型 差分
SARIMA(Seasonal ARIMA)模型
SPSS实例及论文内容
附录
步骤
- 数据预处理:SPSS填补缺失值;生成时间变量、画出时间序列图
- 观察时间序列图,判断有没有季节性波动、且是季度或月度数据
- 季节性规律 + 季节性波动恒定:季节性分解的加法模型
- 季节性规律 + 季节性波动随时间有变化(如递增):乘法模型
- 数据围绕均值上下波动,无趋势、季节性:数据是平稳序列
- 用SPSS专家建模得出最佳模型
- 结果是 ARIMA(p,0,q) 模型,画出时间序列的样本 ACF 和 PACF 图形进行分析;
- 是 ARIMA(p,1,q) 模型,先对数据进行 1 阶差分后,再用 ACF 和 PACF 图形分析;
- 结果与季节性相关(如温特加法乘法模型、SARIMA),用时间序列分解
基本概念
时间序列:也称动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列
组成要素:
- 时间要素:年、季度、月、周、日、小时、分钟、秒
- 数值要素
时点序列:数值要素反映现象在一定时点上的瞬间水平
时期序列:数值要素反映现象在一定时期内发展的结果
时期序列可加、时点序列不可加
时间序列分解
分解为:
- 长期趋势 (Secular trend, T)
- 季节趋势(Seasonal Variation, S) :一般以月、季、周为时间单位,不能以年作单位
-
循环变动( CyclicalVariation, C) :以年为周期
-
不规则变动( IrregularVariation, I) :白噪声 / 扰动项
叠加 / 乘积模型
叠加:数据的因变量/指标数值的最终变动 Y = T+S+C+I
乘积:Y = T×S×C×I
使用时间序列分解为上述模型的条件:
- 数据有年内的周期性,如月份/季度,年份数据就不行
- 在时间序列图上随时间推移,波动越来越大 --- 乘积模型;波动恒定 --- 叠加模型;不存在季节波动 --- 两个都可
使用SPSS的实例
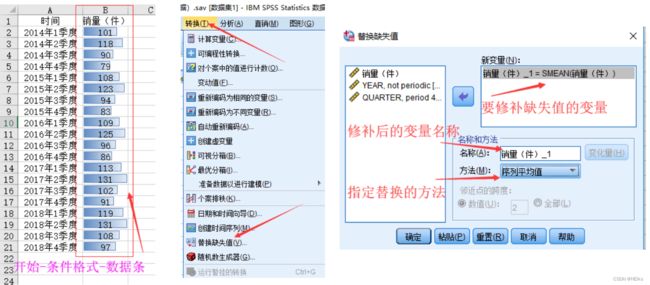
首先处理时间序列中的缺失值:缺失值在首尾,直接删除数据;在中部则不能删除,要替换缺失值
上图中替换缺失值的方法:
- 序列平均值:整个序列的平均数
- 临近点的平均数:相邻若干个点的平均数(默认2个点)
- 临近点的中位数
- 线性插值:相邻的两个点的平均数
- 邻近点的线性趋势:将时期作为x 时间序列值作为y进行回归
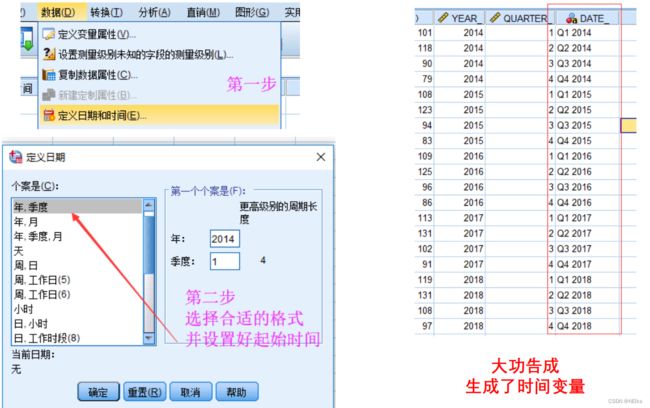
定义时间变量:
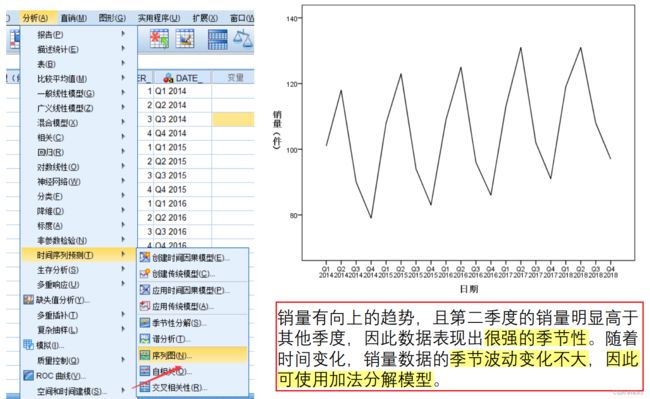
画出时间序列图,看用叠加 or 乘积模型,并对图做解释:有季节周期性,波动不大 - 叠加;季节周期性,波动大 - 乘积
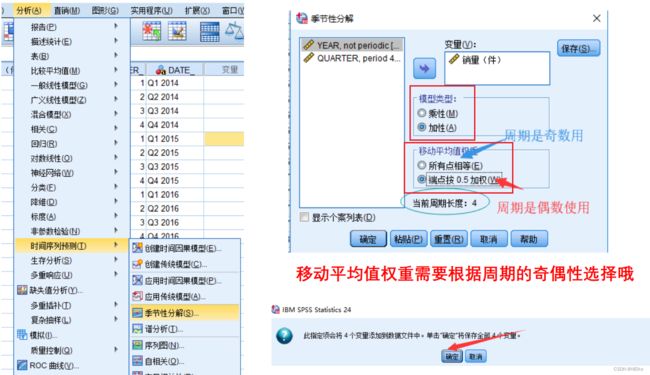
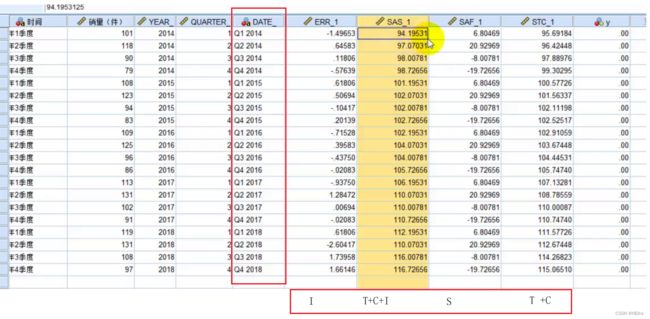
进行季节性分解(即把 Y 分解为 T、S、C、I)
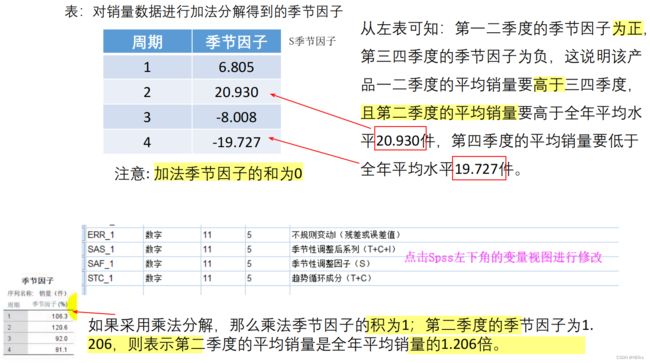
解读结果:季节因子的正负,如果是乘积模型则是倍数关系
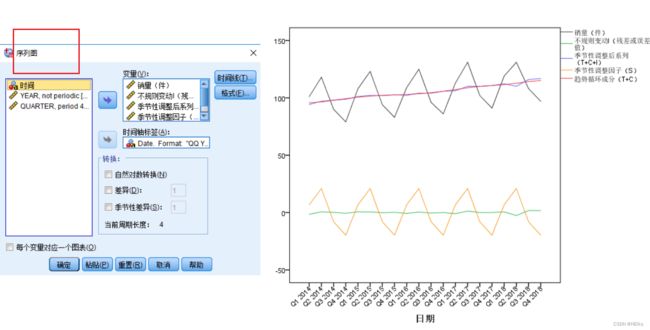
画出分解后的序列图:
步骤
时间序列分解用于预测未来
指数平滑模型
| 名称 | 适用条件 | 与之类似的ARIMA模型 |
| 简单指数平滑法(Simple模型) | 不含趋势T、不含季节S成分 | ARIMA(0,1,1) |
|
线性趋势模型(linear trend)
|
线性趋势、不含季节 |
ARIMA ( 0,2,2 )
|
|
阻尼趋势模型(Damped trend)
|
线性趋势逐渐减弱、不含季节成分
|
ARIMA ( 1,1,2 )
|
|
简单季节性(Simple seasonal)
|
含有稳定的季节成分、不含趋势
|
|
|
温特加法模型(Winters' additive)
|
含有线性趋势和稳定的季节成分
|
|
|
温特乘法模型(Winters' multiplicative)
|
含有线性趋势和不稳定的季节成分
|
不存在 |
Simple模型
| 简单指数平滑法(Simple模型) | 不含趋势T、季节S成分 | ARIMA(0,1,1) |
只能预测往后一期数据!!!由公式决定 因为预测后两期的数据需要后一期的数据,而后一期的数据等待被预测 还未知
线性趋势模型
|
(Holt)线性趋势模型(linear trend)
|
线性趋势、不含季节 |
ARIMA ( 0,2,2 )
|
缺点:对未来预测值过高,特别是长期预测
布朗线性趋势模型
α = β 时,即认为水平与趋势平滑参数相等
阻尼趋势模型
|
阻尼趋势模型(Damped trend)
|
线性趋势逐渐减弱且不含季节成分
|
ARIMA ( 1,1,2 )
|
解决Holt线性趋势模型对未来长期预测值过高:加入阻尼效应
简单季节性
|
简单季节性(Simple seasonal)
|
含有稳定的季节成分、不含趋势
|
温特加法模型
|
温特加法模型(Winters' additive)
|
含有线性趋势和稳定的季节成分
|
SPSS会返回各个参数的估计值,预测型不需要关注参数的显著性,解释型才要
温特乘法模型
|
温特乘法模型(Winters' multiplicative)
|
含有线性趋势和不稳定的季节成分
|
不存在 |
乘法模型预测出来比加法模型的波动大
一元时间序列分析的模型
基础概念
平稳时间序列、白噪声序列
(弱)平稳的条件:
白噪声序列:均值为0的特殊平稳时间序列
有(季节性)波动的不是平稳的时间序列,因为均值在某一季度达到最大,不是固定常数
差分方程及其特征方程
差分:用于转化为平稳的时间序列
AR自回归的差分方程:与自身之前的因素有关
MA移动平均的差分方程:与以往的随机扰动项相关
特征方程的解决定时间序列是否平稳,怎么求特征方程:x的最高阶数就是 y 中滞后的期数
滞后算子
滞后 p 期 就是 L的 p 次方;d 阶差分 就是 (1-L)^p*yt;季节差分 m为周期
AR(p)模型(auto regressive) 自回归
与自身以前的数据有关,所以模型中包含以前的 y;还包含一个单独的参数、随机扰动项:
特征方程判断平稳性
计算的例子
MA(q)模型(moving average)
MA模型和AR模型的关系
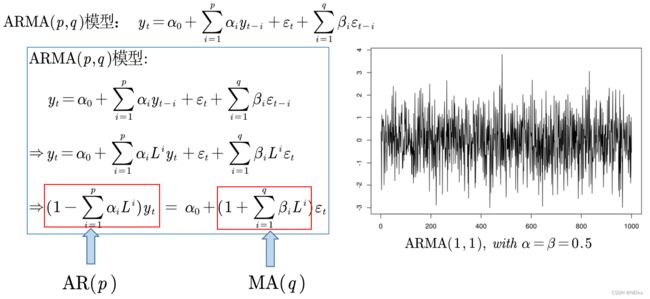
ARMA(p,q)模型
由AR与MA组成,MA一般是平稳的,所以ARMA的平稳性判定方法就是AR的判定方法:特征方程根的模长
选择p、q的方法
ACF自相关系数、PACF偏自相关系数
将数据转化为平稳序列后才能用ACF、PACF;自相关系数可用于判断是否是白噪声
PACF:两个数据的ACF受这两个数中间数据的影响,而PACF剔除了中间数据的影响
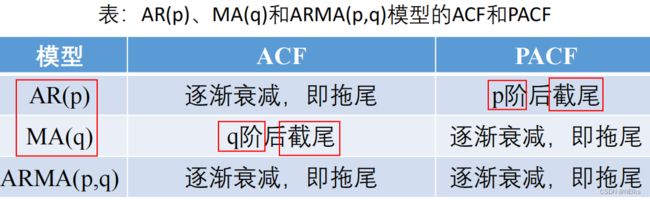
ACF、PACF判断用哪个模型合适:AR MA ARMA
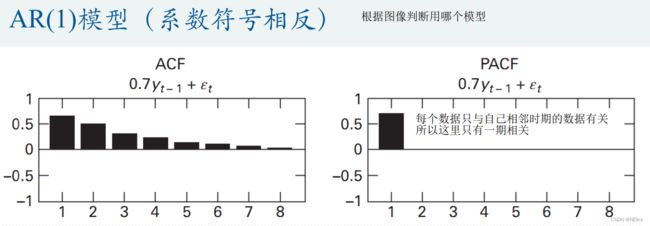
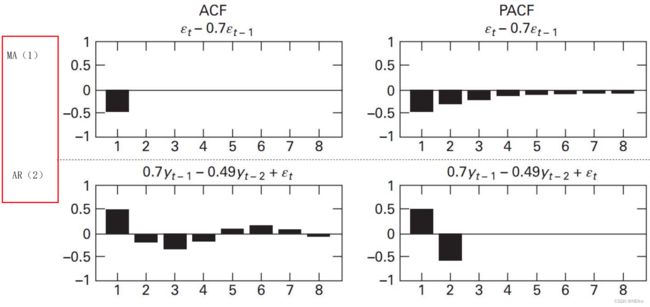
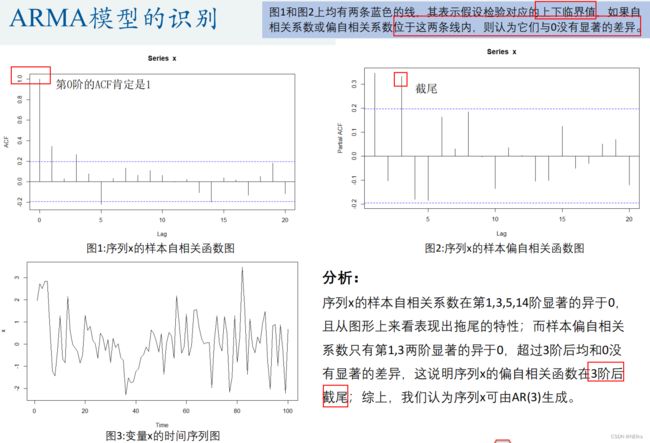
AR模型中有与自己以往数据相关的变量 y ,所以与自身以往有关(没有剔除中间数据关系)的系数ACF拖尾,PACF截尾(PACF剔除了中间数据关系,yt 的值只与 y(t-p) 即前p期的值有关,与再之前的值无关 所以截尾),阶数p就是PACF的截尾处
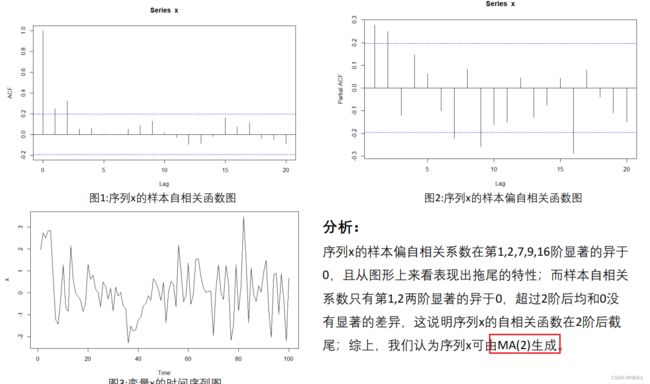
MA中只有随机扰动项有关的系数,所以ACF截尾,但PACF拖尾
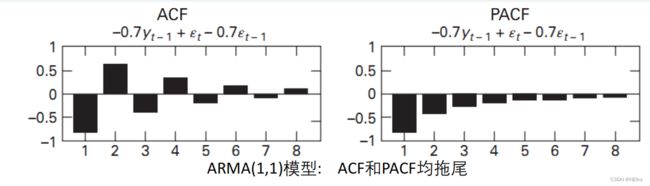
ARMA都拖尾
实际作图中有两条线,线内的值当作0处理:
ARMA很难识别阶数,用极大似然估计
AIC、BIC准则
目的是在模型选择过程中,平衡模型复杂度(模型参数个数决定,越少越好)、模型对数据解释能力(回归中用拟合优度或误差平方和SSE,误差平方和越小、拟合优度越大,解释能力越好;这里使用极大似然估计,极大似然函数的值越大越好)的关系
只追求解释能力:过拟合问题
根据 AIC、BIC 的大小,选出最小的那个模型
检验模型是否识别完全
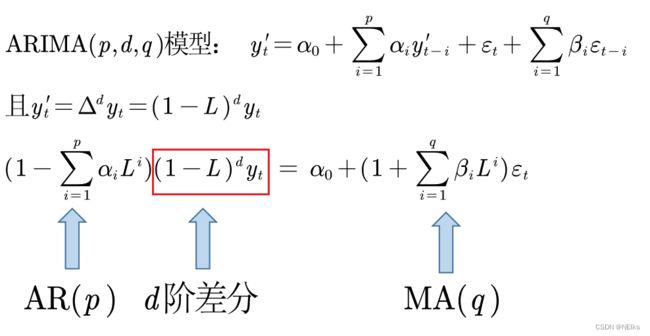
ARIMA(p,d,q)模型 差分
前面讨论的都是平稳时间序列,这里讨论 d 阶单位根的序列 —— 差分处理 转化为平稳的
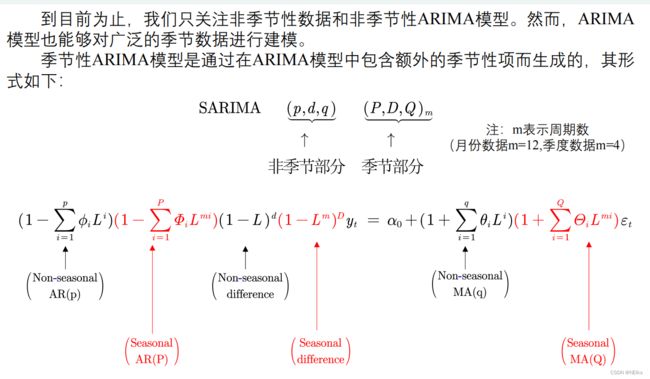
SARIMA(Seasonal ARIMA)模型
加入了季节的因子:
SPSS实例及论文内容
先填补缺失值
画出时序图并分析:图总体有(向上)的趋势,有明显的季节性变化,考虑使用时间序列分解;波动较为恒定,使用加法的时间序列分解
画出加法时间序列分解图并分析:季节因子等(见前面的笔记)
然后我们利用SPSS的专家建模器为我们选择了(温特加法模型)(把下图的工作 原理写入论文):
把温特加法模型的公式及参数解释、SPSS得出的参数估计值写入论文:
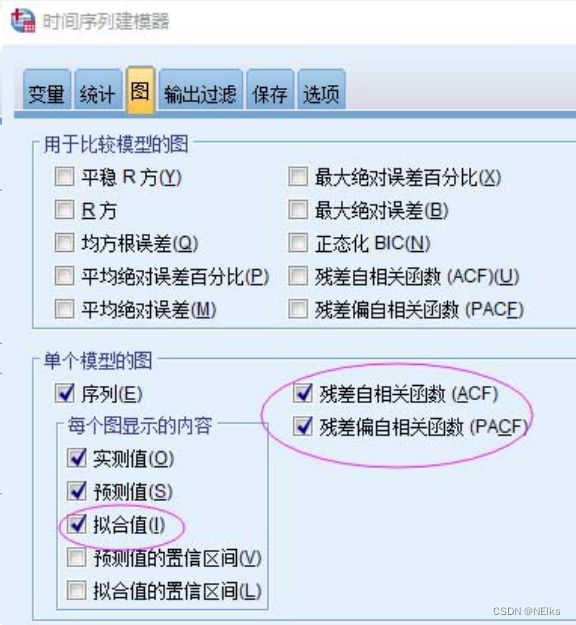
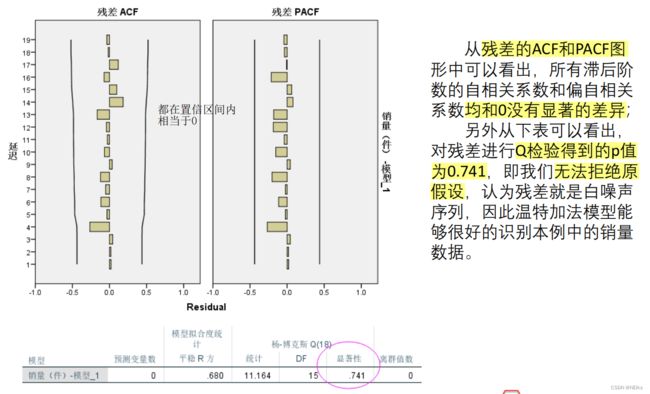
然后对白噪声进行残差检验与分析(SPSS专家建模中勾选下面的残差ACF、PACF):
(把上图和表写入论文)
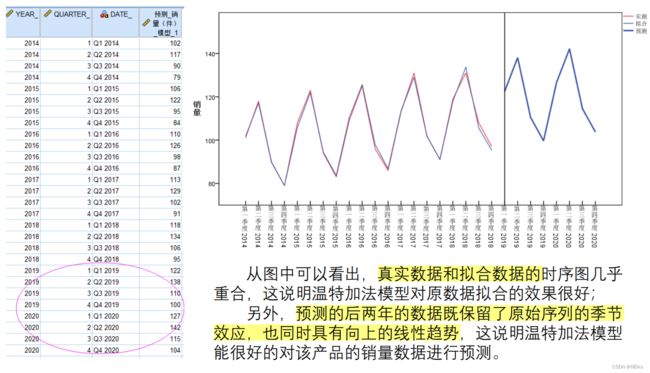
在 95% 置信水平下,我们得到预测值...并进行分析:
根据参数估计值写出公式:
附录
股票预测更好的模型:GARCH模型(广义的自回归条件异方差模型)
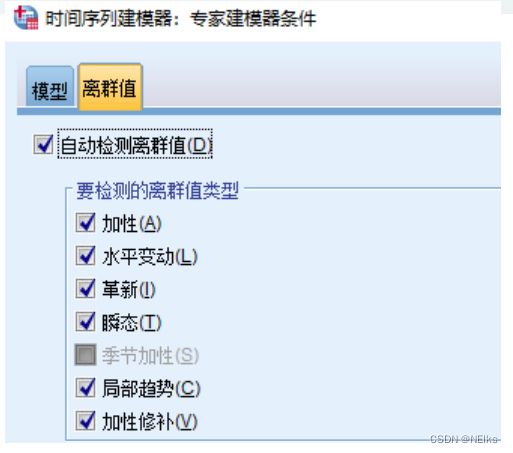
注意异常值,可用SPSS去除异常值: