AcWing239.奇偶游戏 边带权和拓展域并查集

我们可以观察到这样的一个性质:若[l-1, r]中1的个数为偶数,则s[l-1]与s[r]的奇偶性相同,否则s[l-1]与s[r]的奇偶性肯定不同.并且我们发现,对于3个不同的节点x1,x2,x3,如果x1与x2,x2与x3的奇偶性相同,那么x1与x3的奇偶性相同;如果x1与x2,x2与x3的奇偶性都不相同,那么x1与x3的奇偶性相同;如果x1与x2奇偶性相同,x2与x3的奇偶性不同,那么x1与x3的奇偶性不同.这本质上就是异或运算,要快速查询任意两个节点x,y的奇偶性,我们可以使用并查集.因为并查集很擅长处理两个变量的传递性关系的问题.

接下来,我们用两种并查集的解法解决这道题:

1."边带权"

我们用一个并查集先维护s[x,y]的前缀和的奇偶性,让并查集树上每条边带权值,若两个节点的权值相同,则边权是0,不同则为0.

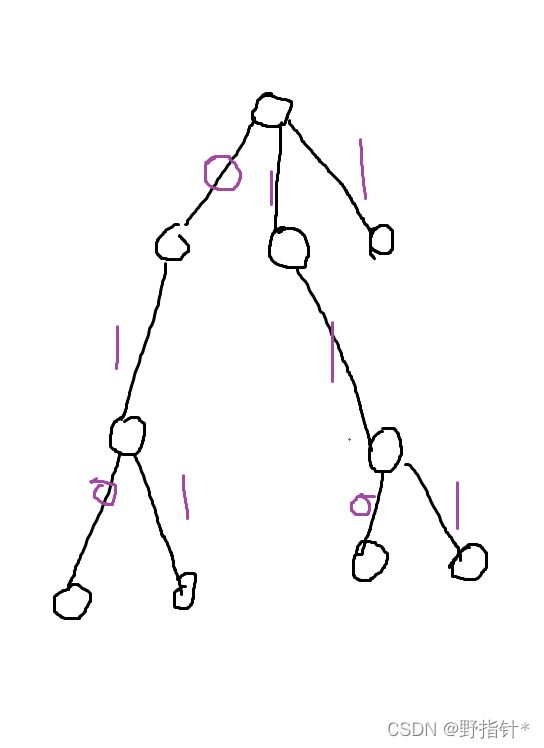
d[x]就表示根节点到x节点的异或和

路径压缩:(xor表示异或)

合并集合:

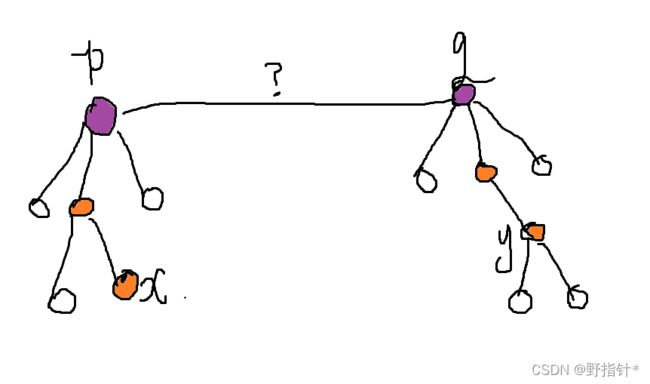
d[x]与d[y]分别表示路径x~p与y~p之间所有的边权的异或和,p~q之间的边权是待求的值,显然路径x~y由路径x~p,y~q与p~q组成,因此x与y的奇偶性关系ans=d[x] xor d[y] xor d[p].对等式两边同时xor ans xor d[p]得到d[p]=d[x] xor d[y] xor ans.

#include 
#define int long long
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define DEBUG freopen("input.in", "r", stdin)
using namespace std;
unordered_map mp{{'e', 0}, {'o', 1}};
vector alls;
struct rec
{
    int x, y, ans;
}q[5010];
int fa[10010], d[10010];
inline int query(int x){
    return lower_bound(alls.begin(), alls.end(), x) - alls.begin() + 1;
}

int find(int x){
    if(x == fa[x])
        return x;
    int root = find(fa[x]);
    d[x] ^= d[fa[x]];
    return fa[x] = root;
}
signed main(){
    IOS;
    // DEBUG;
    int n, m;
    char intg[5];
    cin >> n >> m;
    for (int i = 0; i <= 10010; ++i)
        fa[i] = i;

    for (int i = 1, x, y; i <= m; ++i){
        cin >> x >> y >> intg;
        q[i].x = x - 1;
        q[i].y = y;
        q[i].ans = mp[intg[0]];
        alls.emplace_back(q[i].x - 1);
        alls.emplace_back(q[i].y);
    }
    
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    
    for (int i = 1; i <= m; ++i){
        auto t = q[i];
        int x = query(t.x), y = query(t.y);
        int p = find(x), q = find(y);
        if (p == q){
            if((d[x] ^ d[y]) != t.ans){
                cout << i - 1 << "\n";
                return 0;
            }
        }
        else
            fa[p] = q, d[p] = d[x] ^ d[y] ^ t.ans;
    }
    cout << m << "\n";
}

2."扩展域"

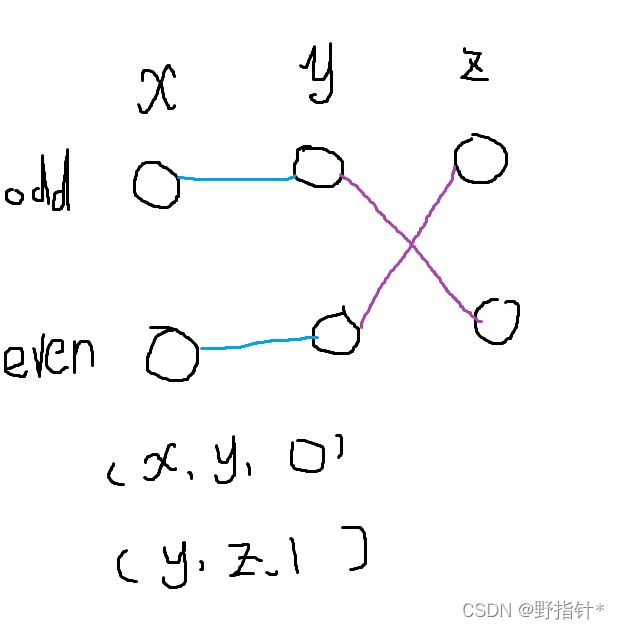
我们可以把每个节点 x 拆分成两个节点x_even, x_odd.其中x_odd表示sum[x]是奇数,x_even表示sum[x]是偶数.我们经常把这两个节点称为x的"奇数域","偶数域".

对于两个节点x, y,答案是ans.

若ans = 0,那么x_odd与y_odd合并,x_even与y_even合并;

若ans = 1,那么x_odd与y_even合并,x_even与y_odd合并.

问题就转化成了验证传递关系是否有矛盾.

若x_odd和y_odd在同一个集合,那么x与y的奇偶性相同,若x_odd与y_even在同一个集合,那么x与y的奇偶性不同.

#include 
// #define LOCAL
#define int long long
using namespace std;
const int N = 30010;
int n, m;
int fa[N];
struct rec{
    int x, y, ans;
};

vector alls;
vector ques;
unordered_map mp{{"even", 0}, {"odd", 1}};
int query(int x){
    return lower_bound(alls.begin(), alls.end(), x) - alls.begin() + 1;
}

int find(int x){
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}
signed main(){
#ifdef LOCAL
    freopen("input.in", "r", stdin);
    freopen("output.out", "w", stdout);
#endif
    cin >> n >> m;
    for (int i = 1; i < 20010; ++i)
        fa[i] = i;

    int l, r;
    string s;
    for (int i = 0; i < m; ++i){
        cin >> l >> r >> s;
        alls.emplace_back(l - 1);
        alls.emplace_back(r);
        ques.push_back({l - 1, r, mp[s]});
    }
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    for (int i = 0; i < ques.size(); ++i){
        auto t = ques[i];
        int x_even = query(t.x), x_odd = x_even + 10005;
        int y_even = query(t.y), y_odd = y_even + 10005;
        int ans_ = t.ans;
        if(ans_ == 0){
            if(find(x_odd) == find(y_even))
                return printf("%d\n", i), 0;
            fa[find(x_even)] = find(y_even);
            fa[find(x_odd)] = find(y_odd);
        }
        else{
            if(find(x_odd) == find(y_odd))
                return printf("%d\n", i), 0;
            fa[find(x_even)] = find(y_odd);
            fa[find(x_odd)] = find(y_even);
        }
    }
    return printf("%d\n", m), 0;
}