算法：（1）剑指offer，python实现

参考

大神
python算法书！

*. 基础

0.1 查找和排序

冒泡排序、插入排序、快速排序、选择排序、归并排序

参考1
参考2

顺序查找	二分查找	哈希表查找	二叉排序树查找
--------	--------	时间O(1)，需要额外的空间

插入排序、冒泡排序、归并排序、快速排序不同算法的优劣

0.1.1 快速排序

关键在于数组中选择一个数字，根据数组中数字的相对于这个基准值的大小，小的排在基准值左边（前面），大的排在基准值后面。实现的办法是，有两个指针，左指针遍历取相对大的数，和右指针所取的相对小的数，两者进行调换，从而逐渐地将大的数放到右边，小的数放到左边。

def quickSort(alist):
    quickSortHelper(alist,0,len(alist)-1)
    
def quickSortHelper(alist,first,last):
    #基本结束条件
    if first<last:
        #分裂为两部分
        splitpoint=partition(alist,first,last)
        print(alist)
        #递归调用
        quickSortHelper(alist,first,splitpoint-1)
        quickSortHelper(alist,splitpoint+1,last)
        
def partition(alist,first,last):
    #选定中值
    mid=alist[first]
    leftmark=first+1
    rightmark=last
    done=False
    while not done:
        while leftmark<=rightmark and alist[leftmark]<=mid:
            leftmark=leftmark+1
        while rightmark>=leftmark and alist[rightmark]>=mid:
            rightmark-=1
        # 两标相错就结束移动
        if rightmark<leftmark:  
            done=True
        # 左右两标指向的值交换，继续移动
        else:
            temp=alist[leftmark]
            alist[leftmark]=alist[rightmark]
            alist[rightmark]=temp
    # 把mid调换到rightmark因为rightmark是新的分界点，刚好是mid值的排序位置。
    temp2=alist[first]
    alist[first]=alist[rightmark]
    alist[rightmark]=temp2
    return rightmark
    
alist=[10,9,8,7,6,5,4,3,2,1,0]
quickSort(alist)

极简法

def quicksort(alist):
    if len(alist) >= 2:
        mid = alist[0]
        left = []
        right = []
        alist.remove(mid)
        for i in alist:
            if i <= mid:
                left.append(i)
            else:
                right.append(i)
        return quicksort(left) + [mid] + quicksort(right)
    else:
        return alist

alist=[10,9,8,7,6,5,4,3,2,1,0]
alist_copy = alist.copy()
print(quicksort(alist_copy))

0.1.2 二分法

要求在排序（部分排序）的数组中，查找一个数字或者统计某个数字出现的次数，可以用二分查找。

2.4.4 动态规划与贪婪算法

动态规划：大问题分解为小问题，小问题存在最优解，则合并之后成为大问题的最优解。

贪婪算法：每一步都是贪婪选择，最后依靠数学方式证明最后达到最优解。

2.4.5 位运算

数字二进制的表示后进行的运算。5种运算：与、或、异或、左移、右移。
左移n位：最左边的n位将被丢弃，最右边补上n个0。
右移n位：最右边的n位将被丢弃，如果是正数，最左边补n个0；如果是负数，最左边补n个1。
00001010 << 2 = 00101000
10001010 << 3 = 01010000

00001010 >> 2 = 00000010
10001010 >> 3 = 11110001
题目
excel中，用AA 表示第27列，AB表示第28列，写出一个函数，输入用字母表示的列表编码，输出它是第几列。

line = input()
n = len(line)
alist = []
for j in line:
    alist.append(int(j,36)-9)

num = 0
for i in range(n):
    num += alist[i] * (26**(n-i-1))

print(num)

题目

11题：旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

分析

如果按照从头到尾遍历，$O(n)$的时间复杂度，则浪费了旋转数组——部分排序的条件。可以使用二分查找，$O(log(n))$的时间复杂度。

依据题意，能够知道，前半、后半部分都为非减情况，同时一般情况下，第一个数大于等于最小数，最后一个数也大于最小数。

使用两个指针，分别指向第一个和最后一个数字。找到中间元素，如果位于后半序列，说明最小值在中间值前面，更新第二个（位于最后）指针到中间位置；如果位于前半序列，说明最小值在中间值后面，更新第一个（位于开始）指针到中间位置。

实现

考虑一般情况

def find2(alist):
    if len(alist)==0: return "enter number list"
    index1 = 0
    index2 = len(alist)-1
    indexmid = index1
    # 为了防止是将0个元素旋转，
    # 则第一个数判断为小于末尾数则是排序完毕的数组。
    while alist[index1] >= alist[index2]:
        if index1 == index2 - 1:
            indexmid = index2
            break
        indexmid = (index1 + index2) // 2
        # 落于两种位置，结合index1/2判断。
        if alist[indexmid] >= alist[index1]:
            index1 = indexmid
        elif alist[indexmid] <= alist[index2]:
            index2 = indexmid
    return alist[indexmid]

alist=[5,6,7,8,9,10,11,12,1,2,3,4]
alist_copy = alist.copy()
print(find2(alist_copy))

12题：矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。 例如
a b c e
s f c s
a d e e
这样的3 X 4 矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

分析

回溯法：像树一样，如果发生条件不符，则回到原位，往别的方向走。

由于有回溯法的递归特质，可以考虑使用栈作为路径。由于不能重复进入路径，所以需要矩阵一样大小的布尔值矩阵。

# 伪代码
def shape()
找到id1（可能有多个位置符合）	
上下左右，找id（i-1）
	Y：更新i，j
	N：返回i，j

def haspath(matrix, rows, cols, path):
    for i in range(rows):
        for j in range(cols):
            if matrix[i * cols + j] == path[0]:
                if findpath(list(matrix), rows, cols, path[1:],i,j):
                    return True

def findpath(matrix, rows, cols, path, i, j):
    if not path:
        return True
    matrix[i*cols + j] = 0
    if j+1 < cols and matrix[i*cols + j + 1]==path[0]:
        return findpath(matrix, rows, cols, path[1:],i, j+1)
    elif j-1 >= 0 and matrix[i*cols + j - 1]==path[0]:
        return findpath(matrix, rows, cols, path[1:],i, j-1)
    elif i+1 < rows and matrix[(i+1)*cols + j]==path[0]:
        return findpath(matrix, rows, cols, path[1:],i+1, j)
    elif i-1 >= 0 and matrix[(i-1)*cols + j]==path[0]:
        return findpath(matrix, rows, cols, path[1:],i-1, j)
    return False

matrix = 'abcesfcsadee'
path = 'bcced'
print(haspath(matrix, 3,4,path))

13题：机器人的运动范围

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

不确定对否

def movingCount(threshold, rows, cols):
    if threshold < 0 or rows <= 0 or cols <= 0:
        return 0
    visited = [False]*(rows*cols)
    count = movingCountCore(threshold, rows, cols, 0,0, visited)
    del(visited)
    return count

def movingCountCore(threshold, rows, cols, row, col, visited):
    count = 0
    if check(threshold, rows, cols, row, col, visited):
        visited[row * cols + col] = True
        count = 1+ movingCountCore(threshold, rows, cols, row-1, col, visited)\
                + movingCountCore(threshold, rows, cols, row+1, col, visited)\
                + movingCountCore(threshold, rows, cols, row, col-1, visited)\
                + movingCountCore(threshold, rows, cols, row, col+1, visited)
    return count

def check(threshold, rows, cols, row, col, visited):
    if row >= 0 and row < rows and col >= 0 and col < cols \
       and getDigit(row) + getDigit(col) <= threshold \
       and not visited[row * cols + col]:
        return True
    return False

def getDigit(num):
    sum1 = 0
    while num > 0:
        sum1 += num%10
        num //= 10
    return sum1

print(movingCount(3, 40,40) )

14题：剪绳子（动态规划、贪婪算法）

剪成若干段，得到各段的乘积最大。

分析（动态规划）

首先定义$f(n)$为长度为$n$的绳子，剪成若干段后各段乘积最大值。假设在$i$处剪了，得到$f(n)=f(i)\ast f(n-i),0<i<n$。所以是递归问题，但是要储存在内存上。

代码

length = int(input())

if length < 2: print(0)
if length == 2: print(1)
if length == 3: print(2)

products = [0] * (length + 1)
products[0] = 0
products[1] = 1
products[2] = 2
products[3] = 3

max1 = 0
for i in range(4,length+1):
    max1  = 0
    for j in range(1,i//2+1):
        product = products[j] * products[i-j]
        if max1 < product:
            max1 = product
        products[i] = max1

max2 = products[length]
print(max2)

分析（贪婪算法）

如果n大于5，则尽量剪长度为3的绳子；当剩下的绳子长度为4时，剪成两段2的绳子。当n大于等于6时，应该剪更短，所以最后都会出现3的长度。

代码

length = int(input())

if length < 2: print(0)
if length == 2: print(1)
if length == 3: print(2)

timesof3 = length//3
# 此时，余下了1（比如4），所以更好的方法是将其剪成2*2而非3*1
if length - timesof3 * 3 == 1:
    timesof3 -= 1

timesof2 = (length - timesof3 * 3) // 2

print((3 ** timesof3)*(2 ** timesof2))

15题：二进制中1的个数

分析

将num位右移1位，不断得到最后一位数，并且运算后去除。
num和1进行求“位与运算”，由于1的左边均为0，所以只要是最后一位是1，则求得1，是0则求得0.
注：尽量用位移来代替除以2，以提高效率。

代码

测试用例：
正数（包括边界值）、负数、0

1. 可能引起死循环的代码（比如无法处理负数）

def NumberOf1(num):
    count = 0
    while num:
        if num & 1:
            count += 1
        num = num >> 1
    return count
num = int(input())
print(NumberOf1(num))

2. 常规解法：通过位移flag来进行各个位的比较，但是需要将flag限制int的条件（即2³²）

def NumberOf1(num):
    count = 0
    flag = 1
    while flag <= 2**32:
        if num & flag:
            count += 1
        flag = flag << 1
    return count
num = int(input())
print(NumberOf1(num))

3. 智商解法。。。
   一个例子：1100，该二进制数减去1的情况下，成为1011，两者再求位与关系，即能够将原来最接近右边的1（即1100的第二个1）的右边（包括本身）全变成0，成为新的数，进行另一轮计算。count++

def NumberOf1(num):
    count = 0
    while num:
        count += 1
        num = num & (num - 1)
    return count
num = int(input())
print(NumberOf1(num))

相关题目

1. 用一条语句判断一个整数是不是2的整数次方。
   分析：易知它的二进制数是只有一位是1，所以在减1 之后，和自己进行位与计算，应该得到全部是0.

def IfSqr(num):
    if num & (num - 1) == 0: return True
    return False

for _ in range(5):
    print(IfSqr(int(input())))

2. 输入两个整数$m$和$n$，计算需要改变$m$的二进制表示中的多少位才可以得到$n$。比如10的二进制表示为1010，13的二进制为1101， 需要改变1010中的三位才可以得到1101。
   分析：需要得到不同的位的数目，所以运行“异或运算”，再按照此前的手法取得该二进制数的1的数目。

def func(num1,num2):
    num = num1 ^ num2
    count = 0
    while num:
        count += 1 
        num = num & (num - 1)
    return count
import sys
for _ in range(5):
    line = sys.stdin.readline().strip().split()
    print(func(int(line[0]),int(line[1]) ) )

18题：删除链表的节点

题意1：给定单向链表的头指针和节点指针，在$O(1)$时间内删除指定的节点。

如果全部都是按照遍历到指定节点的话，会有$O(n)$的复杂时间程度。

（1）如果先把指定的 $i$ 节点的下一个节点j节点复制到 $i$，然后把 $i$ 的指针指向节点 $j$ 的下一个节点，相当于把 $i$ 删除了。时间为$O(1)$。
（2）此外，如果 $i$ 节点在尾部，没有下一个节点，则仍旧需要从最开始进行遍历。
（3）此外，可能存在只有一个节点的情况，则直接删除节点 $i$ 即可。
因此时间复杂度为：$$[(n-1)O(1)+O(n)]/n=O(1)$$

代码

引用链接

class ListNode:
    def __init__(self):
        self.value = None
        self.next_node = None

class Solution:
    def list_generate(self, lst):
        """
        生成链表
        """
        if not lst:
            return None
        list_node = ListNode()
        list_node.value = lst[0]
        if len(lst) == 1:
            list_node.next_node = None
        else:
            list_node.next_node = self.list_generate(lst[1:])
        return list_node

    def find_node(self, node, target_value):
        """
        根据给定的目标值，找出指定节点的位置
        非题目要求，只是为了测试验证
        """
        if not target_value:
            return False
        while node:
            if node.value == target_value:
                return node
            node = node.next_node
        return False

    def delete_node(self, head_node, del_node):
        """
        删除指定节点
        """
        if not (head_node and del_node):
            return False

        if del_node.next_node:
            # 删除的节点不是尾节点，而且不是唯一一个节点
            del_next_node = del_node.next_node
            del_node.value = del_next_node.value
            del_node.next_node = del_next_node.next_node
            del_next_node.value = None
            del_next_node.next_node =None

        elif del_node == head_node:
            # 唯一一个节点，删除头节点
            head_node = None
            del_node = None

        else:
            # 删除节点为尾节点
            node = head_node
            while node.next_node != del_node:
                node = node.next_node

            node.next_node = None
            del_node = None

        return head_node

题意2：在一个排序的链表中，删除链表中重复的节点。

	# 接上例
    def is_repeat(self, node):
        """
        题目二：判断是否与后面的节点重复
        """
        if node.next_node:
            if node.value == node.next_node.value:
                return True
        return False

    def delete_repeat_node(self, head_node):
        """
        题目二：删除重复节点
        """
        node = head_node
        flag = False
        """
        flag说明：例如'a'->'a'，第一次循环删除第二个'a',然后通过这个flag来进行判断上一次操作是否删除重复节点
        如果是的话，再次判断后面还有没有'a'了，没有，则通过这个flag把第一个'a'也应该删除，
        """
        while node:
            if solution.is_repeat(node):
            # 删除重复节点，并且不进行node=node.next_node，可能出现连续多个重复节点
                head_node = self.delete_node(head_node, node)
                flag = True
            else:
                if flag:
                    head_node = self.delete_node(head_node, node)
                    flag = False
                node = node.next_node
        return head_node


if __name__ == '__main__':
    solution = Solution()
    head_node = solution.list_generate(['a', 'a', 'a', 'b', 'c', 'e', 'd', 'd'])# 测试用例

    # ----------------------------------------------------
    # 题目一： 删除指点节点
    # target_value = 'a'
    # target_node = solution.find_node(head_node, target_value)
    # if target_node:
    #     print target_node.value
    # head_node = solution.delete_node(head_node, target_node)
    # ---------------------------------------------------

    # ---------------------------------------------------
    # 题目二：删除重复节点
    head_node = solution.delete_repeat_node(head_node)
    # --------------------------------------------------

    # 输出,打印新链表
    node = head_node
    if node:
        while node:
            print(node.value,'->')
            node = node.next_node
    else:
        print('wrong')

19题：正则表达式匹配

分析

请实现一个函数用来匹配包括’.‘和’‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’'表示它前面的字符可以出现任意次（包含0次）。 在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但是与"aa.a"和"ab*a"均不匹配

分析:参考链接
当模式中的第二个字符不是*时：

1. 如果字符串第一个字符和模式中的第一个字符相匹配，那么字符串和模式都后移一个字符，然后匹配剩余的。
2. 如果字符串第一个字符和模式中的第一个字符相不匹配，直接返回false。

而当模式中的第二个字符是*时：
如果字符串第一个字符跟模式第一个字符不匹配，则模式后移2个字符，继续匹配。如果字符串第一个字符跟模式第一个字符匹配，可以有3种匹配方式：

1. 模式后移2字符，相当于x*被忽略；
2. 字符串后移1字符，模式后移2字符；
3. 字符串后移1字符，模式不变，即继续匹配字符下一位，因为*可以匹配多位；

代码

class Solution:
    def match(self, s, pattern):
        if s == pattern:
            return True
        if not pattern:
            return False
        if len(pattern)>1 and pattern[1] == "*":
            if (s and s[0]==pattern[0]) or (s and pattern[0]=="."):
                # 1. 跳过当下的pattern
                # 2. 算该s匹配，再继续该*的第二次作用。
                # 3.算该s匹配，*只发挥该次作用。
                return self.match(s, pattern[2:]) \
                       or self.match(s[1:], pattern) \
                       or self.match(s[1:], pattern[2:]) 
            else:
                return self.match(s, pattern[2:])
        elif s and (s[0]==pattern[0] or pattern[0]=="."):
            return self.match(s[1:], pattern[1:])
        return False

alist = 'abcd'
test1 = 'a.c.'
test2 = 'ac*bcg*ds*d*'
print(alist,' and ',test1,Solution().match(alist,test1))
print(alist,' and ',test2,Solution().match(alist,test2))

20题：表示数值的字符串判断

分析

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100",“5e2”,"-123",“3.1416"和”-1E-16"都表示数值。 但是"12e",“1a3.14”,“1.2.3”,"±5"和"12e+4.3"都不是。

可能的模式：$A[.[B]][e|EC]$ 或者 $.B[e|EC]$， $e|E$ 表示$e$或$E$。
其中，
$A$和$C$都可能是以$+$或$-$号开头的$0-9$的数位串，$C$是紧跟着$E$或者$e$的指数部分。
$B$是$0-9$的数位串，但不能有开头正负号。
$E$表示指数部分。

代码

参考大神

def scanUnsignedInteger(string):
    if len(string) == 0:
        return False, 0
    i = 0
    while i < len(string) and string[i].isdigit():
        i += 1
    return i > 0, i

def scanInteger(string):
    if len(string) == 0:
        return False, 0
    if string[0] == "-" or string[0] == "+":
        found, index = scanUnsignedInteger(string[1:])
        return found, index + 1
    else:
        return scanUnsignedInteger(string)

def isNumeric(string):
    if len(string) == 0:
        return False
    found_1 = found_2 = found_3 = False
    found_1, index = scanInteger(string)
    string = string[index:]
    is_numeric = found_1
    
    # 如果出现'.'，则接下来是小数部分
    if len(string) > 0 and string[0] == ".":
        string = string[1:]
        found_2, index = scanUnsignedInteger(string)
        string = string[index:]
        # 使用'or'的原因：小数点前面或者后面都可以没有数字
        is_numeric = found_2 or is_numeric
        
    # 如果出现'e'或者'E'，则接下来的数字是指数部分
    if len(string) > 0 and (string[0] == 'e' or string[0] == 'E'):
        string = string[1:]
        found_3, index = scanInteger(string)
        string = string[index:]
        # 使用'and'的原因：e的前面或者后面没有数字，都不合法
        is_numeric = found_3 and is_numeric
    
#     print("found_1: ", found_1, ",found_2: ", found_2, ",found_3: ", found_3, "is_numeric: ", is_numeric)
    return is_numeric and len(string) == 0

【3.4】代码的鲁棒性

23题：链表中环的入口节点

分析

如：在1->2->3->4->5->6->3的链表中，包含一个环，环的入口节点是3。

1. 确定一个链表里面有环
   用两个指针解决问题。P1一次走一步，P2一次走两步（不一定是2倍，较快即可）。当P2（走得快）能够追上P1，说明有环；如果P2走到了链表的末尾，还没有追上P1，说明不包含环。
   解释： 因为是两倍，所以假如环的总长度是N，那么P2能够走2N，P1能够走N，P2能够“套圈”。能够套圈说明差距是N。
2. 找到环的入口
   用两个指针解决问题。P1和P2指向链表的头结点，如果环例有n个节点，那么P1先在环上移动n步，P2再出发，以相同的速度向前移动。当P2到达环的入口节点时，P1应该回到了该入口节点。

使用同样速度一前一后的两个指针，前面的指针先走n步，然后后面的指针和前面的指针一起走，当二者第一次相遇时，慢指针正好走了k步，快指针走了n+k步，都在环入口处。

代码

参考大神

class ListNode:
    """List node."""
    def __init__(self, x):
        self.val = x
        self.next = None

def MeetingNode(headNode):
    if headNode is None:
        return
    slow = headNode.next
    # slow = n1.next = n2
    if slow is None:
        return
    fast = slow.next
    # fast = n2.next = n3
    while fast is not None and slow is not None:
        if fast == slow:
            return fast # 两者相遇
        # 如果不相遇，继续前进
        slow = slow.next
        fast = fast.next
        # 需要两倍前进
        if fast is not None:
            fast = fast.next
    return

def entryNodeOfLoop(headNode):
    meeting_node = MeetingNode(headNode)
    if meeting_node is None:
        return
    
    # 计算环的长度
    n = 1 # 最短两个节点组成环，差距只有 n = 1
    node = meeting_node
    while node.next != meeting_node:
        node = node.next
        n += 1
        
    # 先移动前面的指针n次
    ahead = headNode
    for i in range(n):
        ahead = ahead.next
        
    # 再同时移动两个指针，直到相遇
    behind = headNode
    while ahead != behind:
        ahead = ahead.next
        behind = behind.next
    return ahead

n1 = ListNode(10)
n2 = ListNode(20)
n3 = ListNode(30)
n4 = ListNode(40)
n5 = ListNode(50)
n6 = ListNode(60)
n1.next = n2
n2.next = n3
n3.next = n4
n4.next = n5
n5.next = n6
n6.next = n3 
# n6.next = n3
entry = entryNodeOfLoop(n1)
if entry != None: print(entry.val)
else: print(entry)

24题：反转链表

定义一个函数，输入链表的头节点，反转该链表并输出反转后链表的头节点。

分析

1. 递归
2. 正向遍历

代码

class ListNode:
    """List node."""
    def __init__(self, x):
        self.val = x
        self.next = None
        
def print_list(head_node):
    """Traverse a list and print."""
    vals = []
    while head_node:
        vals.append(head_node.val)
        head_node = head_node.next
    if len(vals) > 0:
        print(" ".join(map(str, vals)))
    else:
        print("This node list is empty!")

def reverseListRecursive(headNode):
    # 防止输入空节点
    if headNode is None:
        return None, None
    # 行进至最后一个，返回本身
    if headNode.next is None:
        return headNode, headNode
    # 递归处：
    new_tail, new_head = reverseListRecursive(headNode.next)
    new_tail.next = headNode # 新的尾部，接现在输入的headNode，实现该部分翻转
    headNode.next = None # 现在输入的headNode应该有None的next，
    return headNode, new_head

    # new_head 就一直不变，
    # 保持是原来最后一个节点作为new_head保持后续的输出。

def reverseList(headNode):
    if headNode is None:
        return
    if headNode.next is None:
        return headNode
    prevNode = headNode
    node = headNode.next
    headNode.next = None
    while node.next != None:
        nextNode = node.next
        node.next = prevNode
        prevNode = node
        node = nextNode
    node.next = prevNode
    return node

n1 = ListNode(10)
n2 = ListNode(20)
n3 = ListNode(30)
n4 = ListNode(40)
n5 = ListNode(50)
n6 = ListNode(60)
n1.next = n2
n2.next = n3
n3.next = n4
n4.next = n5
n5.next = n6
new_tail, new_head = reverseListRecursive(n1)
print(new_head.val)
print("Recursive solution: ")
print_list(new_head)
print("new tail: ")
print_list(new_tail)

n1 = ListNode(10)
n2 = ListNode(20)
n3 = ListNode(30)
n4 = ListNode(40)
n5 = ListNode(50)
n6 = ListNode(60)
n1.next = n2
n2.next = n3
n3.next = n4
n4.next = n5
n5.next = n6

print("Regular solution: ")
new_head2 = reverseList(n1)
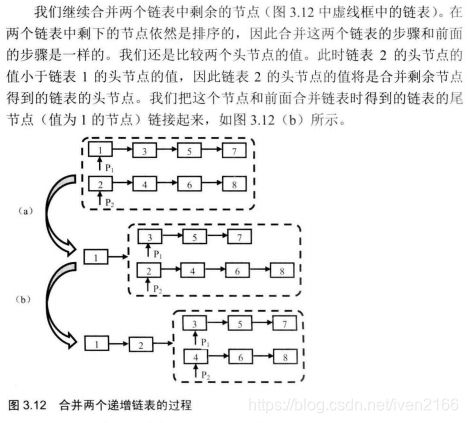
print_list(new_head2)

25题：合并两个排序的链表

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

分析

剑指offer第二版

代码

class ListNode:
    """List node."""
    def __init__(self, x):
        self.val = x
        self.next = None
        
def print_list(head_node):
    """Traverse a list and print."""
    vals = []
    while head_node:
        vals.append(head_node.val)
        head_node = head_node.next
    if len(vals) > 0:
        print(" ".join(map(str, vals)))
    else:
        print("This node list is empty!")

def CombineTwoSortedListNode(head_node1, head_node2):
    # robust
    if head_node1 is None and head_node2 is None:
        return None
    if head_node1 is None:
        return head_node2
    if head_node2 is None:
        return head_node1

    # begin merge
    alistnode = [] # 难以用链表直接保存
    while head_node1 and head_node2:
        if head_node1.val <= head_node2.val:
            alistnode.append(head_node1)
            head_node1 = head_node1.next
        else:
            alistnode.append(head_node2)
            head_node2 = head_node2.next
    while head_node1:
        alistnode.append(head_node1)
        head_node1 = head_node1.next
    while head_node2:
        alistnode.append(head_node2)
        head_node2 = head_node2.next
    for i in range(len(alistnode)-1):
        alistnode[i].next = alistnode[i+1]
    alistnode[len(alistnode)-1].next = None
    return alistnode[0]

# test
n1 = ListNode(1)
n2 = ListNode(2)
n3 = ListNode(3)
n4 = ListNode(4)
n5 = ListNode(5)
n6 = ListNode(6)
n1.next = n3
n3.next = n5

n2.next = n4
n4.next = n6

alistnode = CombineTwoSortedListNode(n1,n2)
print("CombineTwoSortedListNode: ")
print_list(alistnode)


def mergeListNode(head1, head2):
    if head1 is None:
        return head2
    if head2 is None:
        return head1
    if head1.val <= head2.val:
        new_head = mergeListNode(head1.next, head2)
        head1.next = new_head
        # head1由于比较小，直接接上head1.next和head2处理之后的new_head结果。
        return head1
    else:
        new_head = mergeListNode(head1, head2.next)
        head2.next = new_head
        return head2


# test
n1 = ListNode(1)
n2 = ListNode(2)
n3 = ListNode(3)
n4 = ListNode(4)
n5 = ListNode(5)
n6 = ListNode(6)
n1.next = n3
n3.next = n5

n2.next = n4
n4.next = n6

alistnode = mergeListNode(n1,n2)
print("mergeListNode: ")
print_list(alistnode)

26. 树的子结构（待更）

输入两棵二叉树A和B，判断B是不是A的子结构。

分析

代码

【4.2】画图让抽象问题更加形象化

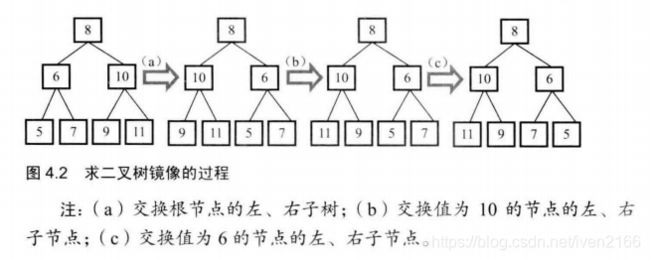
27. 二叉树的镜像

分析

剑指offer第二版

代码

class TreeNode:
    """Tree node."""
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def print_tree(root_node):
    """Travers a tree by level and print."""
    travers = []
    queue = [root_node]
    while len(queue) > 0:
        farther = queue.pop()
        travers.append(farther.val)
        if farther:
            if farther.left:
                queue.insert(0, farther.left)
            if farther.right:
                queue.insert(0, farther.right)
    print(" ".join(map(str, travers)))


def MirrorRecursively(ptree):
    if ptree is None:
        return
    if (ptree.left is None) and (ptree.right is None):
        return
    ptemp = ptree.left
    ptree.left = ptree.right
    ptree.right = ptemp

    if ptree.left:
        MirrorRecursively(ptree.left)
    if ptree.right:
        MirrorRecursively(ptree.right)

n1 = TreeNode(8)
n2 = TreeNode(6)
n3 = TreeNode(10)
n4 = TreeNode(5)
n5 = TreeNode(7)
n6 = TreeNode(9)
n7 = TreeNode(11)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7

print_tree(n1)
MirrorRecursively(n1)
print_tree(n1)

28. 对称的二叉树

分析

注：笔者没法考虑到第三个情况，即全部一样的情况下，“根左右”与“根右左”会一样的结果——但其实并不对称。

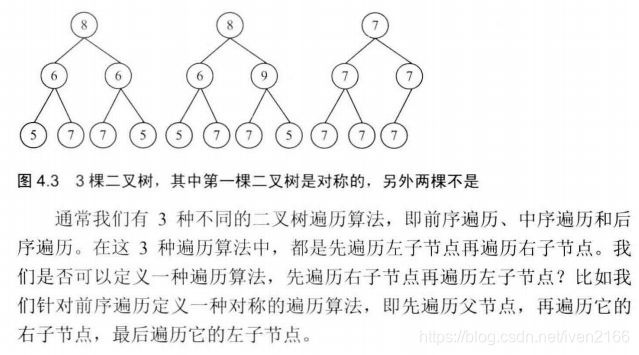
代码

class TreeNode:
    """Tree node."""
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def print_tree(root_node):
    """Travers a tree by level and print."""
    travers = []
    queue = [root_node]
    while len(queue) > 0:
        farther = queue.pop()
        travers.append(farther.val)
        if farther:
            if farther.left:
                queue.insert(0, farther.left)
            if farther.right:
                queue.insert(0, farther.right)
    print(" ".join(map(str, travers)))

def isTreeSymmetrical(root):
    return isTwoTreeSymmetrical(root, root)

def isTwoTreeSymmetrical(root1, root2):
    if root1 is None and root2 is None:
        return True
    if root1 is None or root2 is None:
        return False
    if root1.val != root2.val:
        return False
    return isTwoTreeSymmetrical(root1.left, root2.right) \
           and isTwoTreeSymmetrical(root1.right, root2.left)


n1 = TreeNode(8)
n2 = TreeNode(6)
n3 = TreeNode(6)
n4 = TreeNode(5)
n5 = TreeNode(7)
n6 = TreeNode(7)
n7 = TreeNode(5)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7

print_tree(n1)
print(isTreeSymmetrical(n1))

print("----------------")
print("change n3.val to 9")
n3.val = 9

print_tree(n1)
print(isTreeSymmetrical(n1))

print("----------------")
print("change n3.val to 6, and n3.right is none")
n3.val = 6
n3.right = None

print_tree(n1)
print(isTreeSymmetrical(n1))

29. 顺时针打印矩阵

分析

$PrintMatrixClockwisely$ 是主方程，用于放入list和列、行说明。
$PrintMatrixInCircle$ 是内层的函数，其中只有start作为左上角的出发点，不断地改变。而且能够想到，出发点自加1到最后，必定小于中间半段。

代码

def PrintMatrixClockwisely(numbers, columns, rows):
    if numbers == None or columns<=0 or rows<=0:
        return
    start = 0
    while columns > start *2 and rows > start*2:
        PrintMatrixInCircle(numbers, columns, rows, start)
        start += 1

def PrintMatrixInCircle(numbers, columns, rows, start):
    endX = columns - 1 - start
    endY = rows - 1 - start
    # 从左到右打印一行
    for i in range(start, endX+1):
        number = numbers[start][i]
        print(number)

    # 从上到下打印一列：“终止行号大于起始行号”，才有下方可以走
    if start < endY:
        for i in range(start+1, endY+1):
            number= numbers[i][endX]
            print(number)

    # 从右到左打印一行：“至少有两行两列”
    if start < endX and start < endY:
        for i in range(endX-1, start-1, -1):
            number = numbers[endY][i]
            print(number)

    # 从下到上打印一列：“至少有两列三行”
    if start < endX and start < endY-1:
        for i in range(endY-1, start, -1):
            number = numbers[i][start]
            print(number)

# test
numbers1 = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]]
PrintMatrixClockwisely(numbers1, 4,4)
print("=============================")
numbers2 = [[1,2,3,4]]
PrintMatrixClockwisely(numbers2, 4,1)
print("=============================")
numbers3 = [[1],[2]]
PrintMatrixClockwisely(numbers3, 1,2)

【4.3】举例让抽象问题更加形象化

30. 包含min函数的栈

python的类

分析

首先注意是栈，需要满足，pop的是栈顶。可以有以下渐进的想法：

• 每次压入一个新元素进栈时，将所有元素排序，最小的元素位于栈顶，所以可以在$O(1)$的情况下得到该最小值。——但是不能保证最后压入的元素最先出栈，因为这样不是栈的定义。
• 添加一个变量，存放最小的元素。但是如果当前最小的数被弹出，如何得到第二小的数呢？因为你这个变量只能够存放一个。
• 增加一个辅助栈！
  

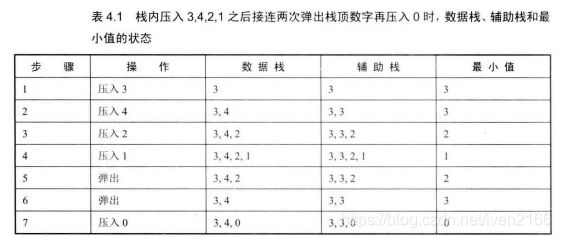
代码（需要定义类）

class StackWithMin:
    def __init__(self):
        self.stack = []
        self.stackMin = []
        self.top = -1 # 之后初始化top加1，才开始在0位开始添加

    def push_func(self, value):
        if len(self.stack)==0:
            self.stackMin.append(value)
        elif  value < self.stackMin[self.top]:
            self.stackMin.append(value)
        else:
            self.stackMin.append(self.stackMin[self.top])
        self.stack.append(value)
        self.top += 1

    def pop_func(self):
        if len(self.stack) > 0 and len(self.stackMin) > 0:
            self.stack.pop()
            self.stackMin.pop()
            self.top -= 1

    def min_func(self):
        if len(self.stack) > 0 and len(self.stackMin) > 0:
            return self.stackMin[self.top]

###测试例
##alist = StackWithMin()
##alist.push_func(5)
##alist.push_func(3)
##alist.push_func(5)
##alist.push_func(1)
##alist.push_func(4)
##for i in range(len(alist.stack)):
##	print(alist.stack, alist.stackMin)
##	print(alist.min_func())
##	alist.pop_func()
##
##	
####[5, 3, 5, 1, 4] [5, 3, 3, 1, 1]
####1
####[5, 3, 5, 1] [5, 3, 3, 1]
####1
####[5, 3, 5] [5, 3, 3]
####3
####[5, 3] [5, 3]
####3
####[5] [5]
####5

31. 栈的压入、弹出序列

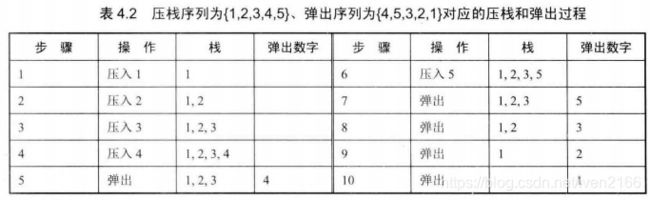
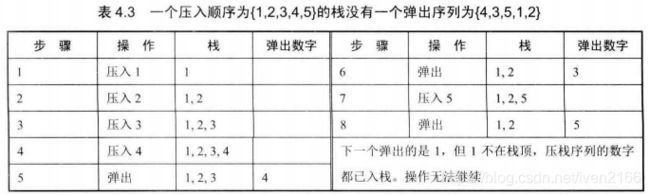
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。

分析

它可以是弹出序列

它不可以是弹出序列

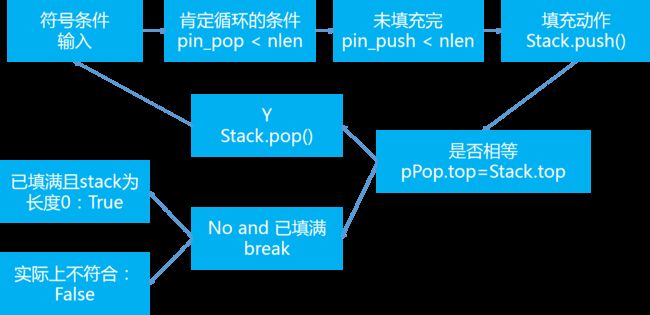
总结规律是：
如果下一个弹出的数字是栈顶的数字，那么直接弹出；如果下一个弹出的数字不在栈顶，则把压栈序列中还没有入栈的数字压入辅助栈，直到把下一个需要弹出的数字压入栈顶位置；如果全部的数字都压入栈顶之后，仍旧没有找到下一个弹出的数字，那么该序列不可能是弹出序列。

• 如果下一个弹出的数字是栈顶的数字，那么直接弹出
• 如果下一个弹出的数字不在栈顶
  • 则把压栈序列中还没有入栈的数字压入辅助栈，直到把下一个需要弹出的数字压入栈顶位置
    • 如果全部的数字都压入栈顶之后，仍旧没有找到下一个弹出的数字，那么该序列不可能是弹出序列。

代码

通过牛客网测试

def IsPopOrder(pPush, pPop, nlength):
    bPossible = False
    if pPush != None and pPop!=None and nlength >0:
        pin_push = 0
        pin_pop = 0
        stack_data = []
        while pin_pop < nlength:
            if pin_push < nlength:
                stack_data.append(pPush[pin_push])
                pin_push += 1                
            if pPop[pin_pop] == stack_data[len(stack_data)-1]:
                stack_data.pop()
                pin_pop += 1
            elif pin_push==nlength and \
               pPop[pin_pop] != stack_data[len(stack_data)-1]:
                break
        if stack_data == []:
            bPossible = True
        return bPossible
    else:
        return bPossible

alist_push = [1,2,3,4,5]
alist_pop  = [4,5,3,2,1]
alist_pop_false = [4,3,5,1,2]
print(IsPopOrder(alist_push, alist_pop, len(alist_push))) # True
print(IsPopOrder(alist_push, alist_pop_false, len(alist_push))) # False

32_1. 从上到下打印二叉树——题目一：不分行，还需要看前序、中序、后序打印

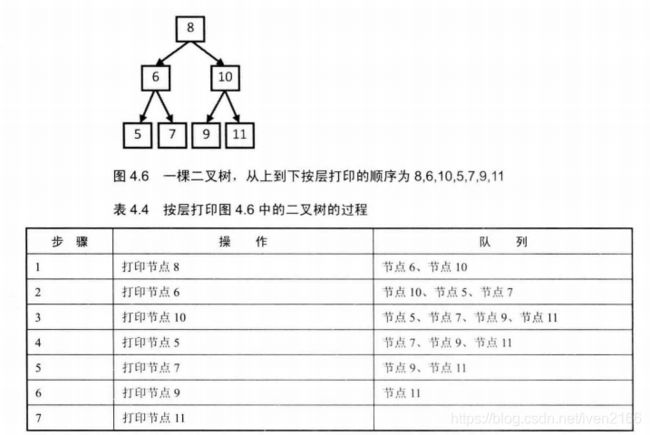
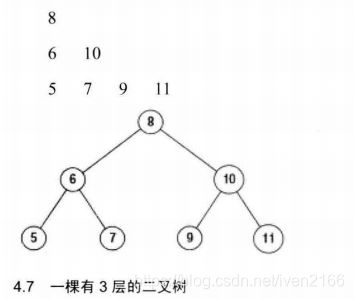
从上到下打印二叉树的每个节点，同一层的节点按照从左到右的顺序打印。例如，输入图4.6的二叉树，则打印出8,6,10,5,7,9,11

代码

class TreeNode:
	def __init__(self, x):
		self.val = x
		self.right = None
		self.left = None

def print_tree(root_node):
	travelers = []
	queue = [root_node]
	while len(queue) > 0:
		father = queue.pop() # 不断地取queue中的最新的一个tree_node,
		# father是一个更新值
		travelers.append(father.val)
		if father:
			if father.left:
				queue.insert(0, father.left)
			if father.right:
				queue.insert(0, father.right)
	print(" ",join( map(str, travelers)) )

# test
n1 = TreeNode(8)
n2 = TreeNode(6)
n3 = TreeNode(10)
n4 = TreeNode(5)
n5 = TreeNode(7)
n6 = TreeNode(9)
n7 = TreeNode(11)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
print_tree(n1)

32_2. 从上到下打印二叉树——题目二：分行，还需要看前序、中序、后序打印

分析

跟上题类似，实际上就是考虑queue及temp两个栈，用来存放当前的node和要打印出来的node，然后再传入子树。

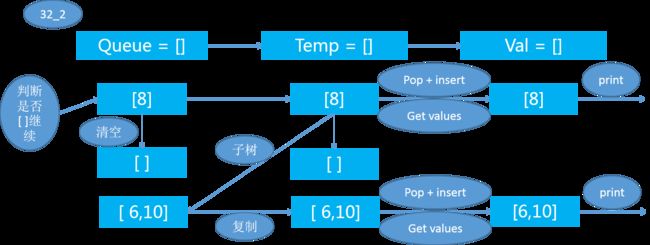
代码

class TreeNode:
	def __init__(self, x):
		self.val = x
		self.right = None
		self.left = None

def print_tree_by_row(root_node):
    queue = [root_node]
    temp = []
    val_PrintNow = []
    while len(queue) > 0:
        temp = queue
        queue = []
        for node in temp:
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        while len(temp) > 0:
            val_PrintNow.insert(0, temp.pop().val)
        print(" ".join(map(str, val_PrintNow)))
        val_PrintNow = []
        
# test
n1 = TreeNode(8)
n2 = TreeNode(6)
n3 = TreeNode(10)
n4 = TreeNode(5)
n5 = TreeNode(7)
n6 = TreeNode(9)
n7 = TreeNode(11)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
print_tree_by_row(n1)

32_3：从上到下打印二叉树——题目三：分行+之字形

分行打印。然后第一行从左到右，第二行从右到左，第三行从左到右，以此类推。

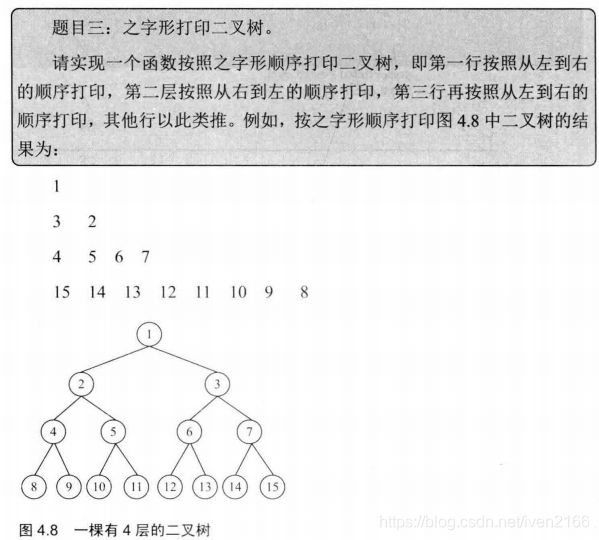
分析

基于上一道题目，同样是分行，我们只需要再加入一个计数器，每print一行就加一，在循环的开头进行计数器的判断，应该给queue左到右还是右到左放入。

代码

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.right = None
        self.left = None

def print_tree_by_row_zhitype(root_node):
    queue = [root_node]
    temp = []
    val_PrintNow = []
    timer = 1
    while len(queue) > 0:
        temp = queue
        queue = []
        for node in temp:
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        if timer%2 == 1:
            while len(temp) > 0:
                val_PrintNow.insert(0, temp.pop().val)
        else:
            while len(temp) > 0:
                val_PrintNow.append(temp.pop().val)
        timer = (timer+1)%2
        print(" ".join(map(str, val_PrintNow)))
        val_PrintNow = []
        
# test
n1 = TreeNode(8)
n2 = TreeNode(6)
n3 = TreeNode(10)
n4 = TreeNode(5)
n5 = TreeNode(7)
n6 = TreeNode(9)
n7 = TreeNode(11)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n3.left = n6
n3.right = n7
print_tree_by_row_zhitype(n1)

33. 二叉搜索树的后序遍历

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

分析

由于每个节点的左子树的值都小于该节点，右子树则值都大于该节点，可以利用循环来判断。
转载大神

代码

def VarifySequenceOfBST(seq):
    return vs_core(seq, 0, len(seq) - 1)
    
def vs_core(seq, s, e):
    if len(seq) == 0:
        return False
    if len(seq) == 1:
        return True
    root = seq[e]
    # 判断左子树是否小于根
    i = s
    while i < e and seq[i] < root:
        i += 1
    if i == e:
        return True
    # 记录左子树的最后一个点的下标
    left_e = i - 1
    # 判断右子树是否大于根
    while i < e:
        if seq[i] < root:
            return False
        i += 1
    # 递归判断
    is_left = True
    is_right = True
    if left_e >= s:
        is_left = vs_core(seq, s, left_e)
    if left_e + 1 < e:
        is_right = vs_core(seq, left_e+1, e-1)
    return is_left and is_right
# test
seq = [5,7,6,9,11,10,8]
# seq = [7,4,6,5]
print(VarifySequenceOfBST(seq))

34. 二叉树中和为某一值的路径

给出一个二叉树，以及预期的路径（到达叶节点）求和，求所有可能的路径。

分析

1. 从根节点开始遍历，只能够进行前序遍历
2. 有一个序列储存当前所有遍历值，能够判断加和是否为预期值
3. 如果想要更方便地遍历，需要加入递归
4. 每一个结点，由于到达它的路径唯一，所以当前求和值也是唯一的，可以储存起来作为形参，供给下一步递归所用！
5. 更多注意点在代码中

代码

class TreeNode:
	def __init__(self, x):
		self.val = x
		self.left = None
		self.right = None

def FindPath(root_node, expect_sum):
	current_sum = 0 # 第一个递归的值，起点为0
	current_path = []
	FindPathCore(root_node, expect_sum, current_sum, current_path)

def FindPathCore(root_node, expect_sum, current_sum, current_path):
	current_sum = current_sum
	current_path = current_path
	current_sum += root_node.val
	current_path.append(root_node.val)
	# 判断递归终止条件，遍历到了叶节点
	isLeaf = root_node.left==None and root_node.right==None
	if isLeaf and current_sum == expect_sum:
		print("We have found a path: ")
		print(" ".join(map(str, current_path)) )
		print()
	# 如果不是叶节点，则前序遍历它
	if root_node.left != None:
		FindPathCore(root_node.left, expect_sum, current_sum, current_path)
	if root_node.right != None:
		FindPathCore(root_node.right, expect_sum, current_sum, current_path)
	current_path.pop()
	'''
	最后一句：要注意肯定要在退出子节点返回父节点时，要删除该子节点，
	这一块比较难想出来。理解：假设我们在A层进入了 “if root_node.left != None:”
	这一行，导入的是当前的current_path，那么进入之后到达B层，
	假设它立刻就跳到叶节点，所以不用跳进“if root_node.left != None:”
	和 “if root_node.right != None:”这两行，那么它要接着到刚才A层的下一行，
	也就是"if root_node.right != None:"，它必须要返回父节点，那么在B层那会最后，
	需要把path最后一个pop出来。
	
	 *！可以验证的是，当程序跑完之后，我们再调用current_path，
	 会发现它实际上是最后那个符合条件的path，去掉最后一个元素。
	'''

# test
n1 = TreeNode(1)
n2 = TreeNode(2)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5)
n6 = TreeNode(11)
n7 = TreeNode(4)
n8 = TreeNode(8)
n9 = TreeNode(3)
n10 = TreeNode(7)
n11 = TreeNode(7)
n12 = TreeNode(7)

n1.left = n2
n1.right = n3
n2.left = n4
n2.right=n5
n3.left = n6
n3.right = n7
n4.left = n8
n4.right = n9
n5.left = n10
n7.left = n11
n7.right = n12

FindPath(n1, 15)

【4.4】分解让复杂问题简单化（分治法）

35. 复杂链表的复制

题目：请实现ComplexListNodeClone(ComplexListNode)函数，复制一个复杂链表。复杂链表中，每个节点有一个指针指向下一个节点，还有另外一个指针，可以指向任意节点或者是null。

分析

哈希表介绍
最后还是用了书本第三种方法，哈希表还不会用。
分析见代码。

代码

class ComplexListNode:
    def __init__(self, x):
        self.val = x
        self.next = None
        self.sibling = None

def printListNode(phead):
    pnode = phead
    while(pnode != None):
        if pnode.next!=None:
            print(pnode.val, " next => ", pnode.next.val)
        if pnode.sibling != None:
            print(pnode.val, " sibling => ", pnode.sibling.val)
        pnode = pnode.next
    
# （1）把clone复制到每个listnode后面
def CloneNodes(phead):
    pnode = phead
    while(pnode != None):
        # 1. 创建clone，并且复制内容和next
        Comlistnode_clone = ComplexListNode(pnode.val)
        Comlistnode_clone.next = pnode.next
        Comlistnode_clone.sibling = None
        # 2. 接到后面
        pnode.next = Comlistnode_clone 
        pnode = Comlistnode_clone.next # 到达下一个原生listnode

# （2）把sibling复制到每一个clone的listnode里面
def ConnectSiblingNodes(phead):
    pnode = phead
    while(pnode != None):
        Comlistnode_clone = pnode.next
        if(pnode.sibling != None):
            # 需要为原生node的sibling的next，是跳到这个sibling复制的node
            Comlistnode_clone.sibling = pnode.sibling.next
        pnode = Comlistnode_clone.next

# （3）把这个包含原生链以及复制链，拆分为两个
def ReconnectNodes(phead):
    pnode = phead
    Comlistnode_clone_head = None
    Comlistnode_clone = None

    # 处理第一个
    if(pnode != None):
        Comlistnode_clone_head = pnode.next
        Comlistnode_clone = pnode.next
        # 到原生node的复制的后面，也就是原生node第二位
        pnode.next = Comlistnode_clone.next 
        pnode = pnode.next

    while(pnode != None):
        Comlistnode_clone.next = pnode.next # 赋值第二位的复制
        Comlistnode_clone = Comlistnode_clone.next
        pnode.next = Comlistnode_clone.next
        pnode = pnode.next

    return Comlistnode_clone_head

def ComplextListNode_clone(phead):
    CloneNodes(phead)
    ConnectSiblingNodes(phead)
    return ReconnectNodes(phead)

n1 = ComplexListNode(1)
n2 = ComplexListNode(2)
n3 = ComplexListNode(3)
n4 = ComplexListNode(4)
n5 = ComplexListNode(5)

n1.next = n2
n2.next = n3
n3.next = n4
n4.next = n5
n5.next = None

n1.sibling = n3
n2.sibling = n5
n4.sibling = n2

clonenodehead = ComplextListNode_clone(n1)
print("n1")
printListNode(n1)
print()
print("clonenodehead")
printListNode(clonenodehead)

'''
结果
n1
1  next =>  2
1  sibling =>  3
2  next =>  3
2  sibling =>  5
3  next =>  4
4  next =>  5
4  sibling =>  2

clonenodehead
1  next =>  2
1  sibling =>  3
2  next =>  3
2  sibling =>  5
3  next =>  4
4  next =>  5
4  sibling =>  2
'''

36. 二叉搜索树以及双向链表

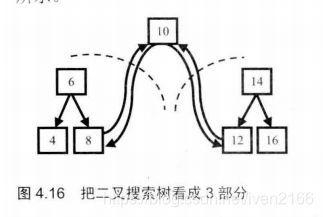
题目：输入一棵二叉搜索树，将该树转化为排序的双向二叉树。要求不创建任何新的节点，只能调整树中的指针的指向。（在原有的二叉搜索树上操作）

代码（该题先上代码，再分析）

class TreeNode:
	def __init__(self, x):
		self.val = x
		self.left = None
		self.right = None
def convert(root_node):
	last_node_in_list = [None]
	convert_core(root_node, last_node_in_list)
	head_node = last_node_in_list[0]
	while head_node is not None and head_node.left is not None:
		head_node = head_node.left
	return head_node

def convert_core(root_node, last_node_in_list):
	if root_node is None:
		return
	curr = root_node
	if curr.left is not None:
		convert_core(curr.left, last_node_in_list)
	curr.left = last_node_in_list[0]
	if last_node_in_list[0] is not None:
		last_node_in_list[0].right = curr
	last_node_in_list[0] = curr
	if curr.right is not None:
		convert_core(curr.right, last_node_in_list)

# test
n1 = TreeNode(10)
n2 = TreeNode(6)
n3 = TreeNode(14)
n4 = TreeNode(4)
n5 = TreeNode(8)
n6 = TreeNode(12)
n7 = TreeNode(16)

n1.left  = n2
n2.left  = n4
n2.right = n5
n1.right = n3
n3.left  = n6
n3.right = n7

head = convert(n1)
while head:
    print(head.val, end = " ")
    head = head.right

'''result
4 6 8 10 12 14 16 
'''

分析

1. 二叉搜索树的特点是，中序遍历即为排序的遍历
2. 需要进行抽象化的迭代
3. 利用分拆的方式分析：

设定一个convert_core()函数作为处理的函数，传入n1（10）

1. 由于需要遍历，所以需要在第一行判断是否为None，如果是则return，不是则往下走
2. curr作为根节点，判断左子树是否为None，不是则进行左子树的处理，迭代convert_core()
3. 需要将新的左子树以及n1（10）用双向链连接起来；此时，n5（8）为储存的last_node_in_list[0]，因此，n5和n1用
   curr.left = last_node_in_list[0]
   进行连接；此外，如果现在的last_node_in_list[0]不为None的话（需要判断因为可能为子树的None子树），它的right为curr
   也就是n5（8）的right需要为n1（10）。至此，左子树处理完毕，并且和根curr进行left以及right的连接
4. 此时，last_node_in_list[0] 应该储存根curr也就是n1（10），然后再处理右子树。
   为什么最后不用定义n1（10）和n6（12）的连接呢？因为，n6作为新的根curr，届时函数会处理left连接到n1.
   

37. 序列化和反序列化二叉树

题目：设计两个函数，分别来序列化和反序列化二叉树。

分析

1. 第一种思路是，给出前序和中序，来唯一地构建二叉树
2. 其实，应该设计一种，可以唯一地进行构建，也就是在子节点为None时，加入特殊的分别字符
3. 再于该序列化的序列，生成二叉树

代码

class TreeNode:
    """Tree node."""
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
        
def print_tree_by_row(root_node):
    queue = [root_node]
    temp = []
    val_PrintNow = []
    while len(queue) > 0:
        temp = queue
        queue = []
        for node in temp:
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        while len(temp) > 0:
            val_PrintNow.insert(0, temp.pop().val)
        print(" ".join(map(str, val_PrintNow)))
        val_PrintNow = []

# 函数开始
def Serialize(root_node, new_serial_list):
    if (root_node is None):
        new_serial_list.append("$,")
        return
    new_serial_list.append(str(root_node.val)+',')
    Serialize(root_node.left, new_serial_list)
    Serialize(root_node.right, new_serial_list)

def BeforeDeSerialize(serial_list):
    serial_list = "".join(map(str,serial_list))
    return DeSerialize(serial_list.split(",") )

def DeSerialize(serial_list_num):
    if len(serial_list_num) == 0:
        return None, ""
    if serial_list_num[0] == "$":
        return None, serial_list_num[1:]
    root_node = TreeNode(serial_list_num[0])
    root_node.left, serial_list_num = DeSerialize(serial_list_num[1: ])
    root_node.right, serial_list_num= DeSerialize(serial_list_num)
    return root_node, serial_list_num

n1 = TreeNode(1)
n2 = TreeNode(2)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5)
n6 = TreeNode(6)

n1.left = n2
n2.left = n4
n1.right= n3
n3.left = n5
n3.right= n6

serial_list1 = []
Serialize(n1, serial_list1)
print(" ".join(map(str, serial_list1)))
# 1, 2, 4, $, $, $, 3, 5, $, $, 6, $, $,

new_root_node, slist = BeforeDeSerialize(serial_list1)
print(slist)
print_tree_by_row(new_root_node)

''' result
1, 2, 4, $, $, $, 3, 5, $, $, 6, $, $,
['']
1
2 3
4 5 6
'''

38. 字符串的排列

题目：输入一个字符串，打印出字符的所有排列。比如输入abc，返回abc，acb，bac，bca，cab，cba

分析

把大问题拆解为小问题，获得原序列后，
（1）固定第一个字符，寻找后面的字符串所有排列（递归）；
（2）将第一个字符和后面字符串的所有字符进行交换，再进行后面的查找（递归）。
本质上是递归。

代码

参考非常易懂的版本：链接

def permutation(s):
    if len(s) <= 1:
        return [s]

    str_list = []
    for i in range(len(s)):
        for j in permutation(s[0:i] + s[i+1:]): # 除开i以外的所有字符中选j
            str_list.append(s[i] + j)
    return str_list

permutation_repeat = permutation(input())
permutation_no_repeat = list(set(permutation_repeat ))
print('permutation with repeat: ', len(permutation_repeat), permutation_repeat )	
print('permutation without repeat: ', len(permutation_no_repeat), permutation_no_repeat )

# abb
# permutation with repeat:  6 ['abb', 'abb', 'bab', 'bba', 'bab', 'bba']
# permutation without repeat:  3 ['bba', 'bab', 'abb']

38-2. 字符串的组合

题目：输入一个字符串，打印出字符的所有排列。比如输入abc，返回a,b,c,ab,ac,bc, abc
输入abcd，返回a,b,c,d, ab,ac,ad,bc,bd,cd, abc,abd,acd,bcd, abcd

分析

代码

def compose_str(str_input):
    li = [i for i in str_input] # 单独列出来，['a','b','c']
    final_li = [] # 最后输出结果
    for m in range(len(li)): # 组合的字符串长度m是从1到str_input的长度
        if m == 0:
            final_li.extend([i for i in li])
        elif m == 1:
            for n in range(len(li)):
                final_li.extend([ li[n] + i for i in li[n+1:] ])
        else:
            final_li.extend(''.join(li[:m]) + i for i in li[m:])

    return final_li

final_li = compose_str(input())
print(final_li)

39. 数组中出现次数超过一半的数字

代码

def more_than_half_num1(numlist):
    length = len(numlist)
    result = numlist[0]
    times = 1
    for i in range(length):
        if times == 0:
            result = numlist[i]
            times = 1
        elif numlist[i] == result:
            times += 1
        else:
            times -= 1
    return result

def partition(data, s, e):
    if s == e:
        return s
    small = s                                           # 以第一个为计数器
    pivot_index = s                                     # 以第一个为比较标准
    pivot_value = data[pivot_index]
    for i in range(s, e):
        if data[i] < pivot_value:                       # 把小值放在左边
            small += 1
            data[i], data[small] = data[small], data[i] # 
    data[small], data[s] = data[s], data[small]         # 最后把这个大的标准，和小值集合最后一个做交换
    return small                                        # 返回把数据二分的标准值的index
    
def more_than_half_num2(numlist):
    # check
    length = len(numlist)
    middle = length >> 1
    start = 0
    end = length - 1
    index = partition(numlist, start, end)
    while(index != middle):
        if(index > middle):
            end = index - 1
            index = partition(numlist, start, end)
        else:
            start = index + 1
            index = partition(numlist, start, end)

    result = numlist[index]
    return result

import sys
# list1 = [int(i) for i in sys.stdin.readline().strip().split()]
list2 = [5,2,4,5,2,5,5,5,9,100,5,5,5]
print(more_than_half_num1(list2))
print(more_than_half_num2(list2))

'''
超过一半，说明数组的中位数是该数字。两种方法。
（1）递归：寻找中间的index
（2）记录数字与出现次数
'''