day19 - 使用高通滤波提取图像边缘
在OpenCV中,对于图像或者视频的处理都或多或少的会涉及傅里叶变换的概念。在数学上,傅里叶变换是指所有的波形都可以由一系列简单且频率不同的正弦曲线叠加得到。也就是说,人们所看到的波形都是由其他波形叠加得到的。这个概念对操作图像非常重要,因为这样我们可以区分图像哪些区域的图像像素值变化特别强,哪些区域变化不那么强,从而可以任意得标记噪声区域、感兴趣的区域、前景和背景等。
本期我们主要来介绍傅里叶变换在图像处理中的应用,学习使用高通滤波提取图像边缘。
完成本期内容,你可以:
- 了解傅里叶变换的基本定义和原理
- 掌握使用傅里叶变换处理图像的基本流程
- 掌握使用高通滤波对图像提取图像边缘的代码实现
若要运行案例代码,你需要有:
-
操作系统:Ubuntu 16.04
-
工具软件:PyCharm 2020.1.5, Anaconda3 2020.07
-
硬件环境:无特殊要求
-
核心库:python 3.6.13, opencv-python 3.4.2.16
点击下载源码
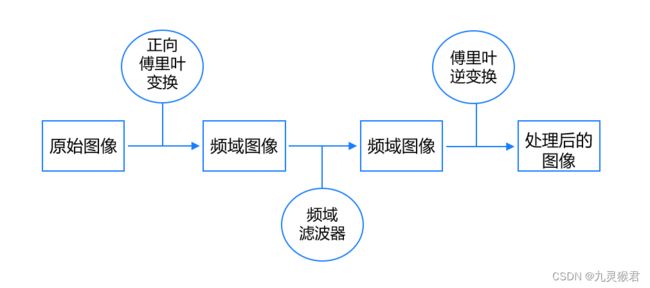
傅里叶变换的流程
针对数字图像的傅里叶变换是将原始图像通过傅里叶变换转换到频域,然后在频域中对图像进行处理的方法。
傅里叶变换
OpenCV中实现傅里叶变换的函数是 cv2.dft(),输出的结果是双通道的。第一个通道是结果的实数部分,第二个通道是结果的虚数部分,并且输入图像要首先转换成 np.float32格式。其语法格式如下:
dst = cv2.dft(src, dst, flags, nonzeroRows)
参数说明:
- src:输入图像,需要通过np.float32转换格式
- dst:输出图像,包括输出大小和尺寸
- nonzeroRows:当参数不为零时,函数假定只有nonzeroRows输入数组的第一行(未设置)或者只有输出数组的第一个(设置)包含非零,因此函数可以处理其余的行更有效率,并节省一些时间;这种技术对计算阵列互相关或使用DFT卷积非常有用
- flags表示转换标记
| 参数值 | 含义 |
|---|---|
| DFT _INVERSE | 执行反向一维或二维转换,而不是默认的正向转换 |
| DFT _SCALE | 缩放结果,由阵列元素的数量除以它 |
| DFT _ROWS | 执行正向或反向变换输入矩阵的每个单独的行,该标志可以同时转换多个矢量,并可用于减少开销以执行3D和更高维度的转换等; |
| DFT _COMPLEX_OUTPUT | 执行1D或2D实数组的正向转换,这是最快的选择,默认功能 |
| DFT _REAL_OUTPUT | 执行一维或二维复数阵列的逆变换,结果通常是相同大小的复数数组,但如果输入数组具有共轭复数对称性,则输出为真实数组 |
np.fft.fftshift(img)
将图像中的低频部分移动到图像的中心,其语法格式如下:
np.fft.fftshift(img)
参数说明:
- img:输入的图片
cv2.magnitude()
由于输出的频谱结果是一个复数,需要调用 cv2.magnitude() 函数将傅里叶变换的双通达结果转换为0到255的范围。其语法格式如下:
cv2.magnitude(x, y)
参数说明:
- x表示浮点型X坐标值,即实部
- y表示浮点型Y坐标值,即虚部
np.fft.ifftshift(img)
将图像的低频和高频部分移动到图像原来的位置,其语法格式如下:
np.fft.ifftshift(img)
参数说明:
- img:输入的图片
傅里叶变换逆变换
在OpenCV中,通过函数 cv2.idft()函数实现傅里叶逆变换,其返回结果取决于原始图像的类型和大小,原始图像可以为复数或实数,同时也要注意输入图像需要先转换成 np.float32格式,其语法格式如下:
dst = cv2.idft(src[, dst[, flags[, nonzeroRows]]])
参数说明:
- x表示浮点型X坐标值,即实部
- y表示浮点型Y坐标值,即虚部
OpenCV中提供了cv2.drawContours()函数来绘制图像轮廓。
函数原型:image=cv.drawContours(image, contours, contourIdx, color[, thickness[, lineType[, hierarchy[, maxLevel[, offset]]]]])
image为目标图像,绘制了边缘的原始图像。
参数描述如下:
- image:待绘制轮廓图像。
- contours:需要绘制的轮廓。
- contourIdx:需要绘制的边缘索引。
- color:绘制的颜色,用 BGR 格式表示。
- thickness:可选参数,表示绘制轮廓时所用的画笔粗细。
- lineType:可选,绘制的线型。
- hierarchy:对应函数cv2.findContours()所输出的层次信息。
- maxLevel:该参数控制绘制的轮廓层次深度。
- offset:偏移参数。
具体步骤
使用高通滤波提取图像边缘。
步骤一:创建项目工具
创建项目名为使用高通滤波提取图像边缘,项目根目录下新建code文件夹储存代码,新建dataset文件夹储存数据,项目结构如下:
使用高通滤波提取图像边缘 # 项目名称
├── code # 储存代码文件
├── dataset # 储存数据文件
注:如项目结构已存在,无需再创建。
步骤二:正向傅里叶变换
- 导入所需模块:OpenCV、NumPy、Matplotlib ;
- 读取
dataset文件夹下的cat.png图片; - 进行正向傅里叶变换;
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
img = cv2.imread('../dataset/cat.png', 0)
# 傅里叶变换
fimg = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 将低频转移到图像中心
fshift = np.fft.fftshift(fimg)
步骤三:高通滤波处理
- 设置高通滤波器;
- 将高通滤波器与傅里叶变换后的图像相乘;
代码实现
# 设置高通滤波器
rows, cols = img.shape # 获取图像属性
crow, ccol = int(rows / 2), int(cols / 2) # 找到傅里叶频谱图的中心点
# 中心点加减30,刚好形成一个定义尺寸的滤波大小,然后设置为0
fshift[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0
步骤四:傅里叶逆变换
- 进行傅里叶逆变换;
- 将数据由频域空间转化为空间域;
- 展示图像;
代码实现
# 傅里叶逆变换
ishift = np.fft.ifftshift(fshift) # 将低频移动到原来的位置
iimg = cv2.idft(ishift) # 使用cv2.idft进行傅里叶的反变化
iimg = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1]) # 转化为空间域内
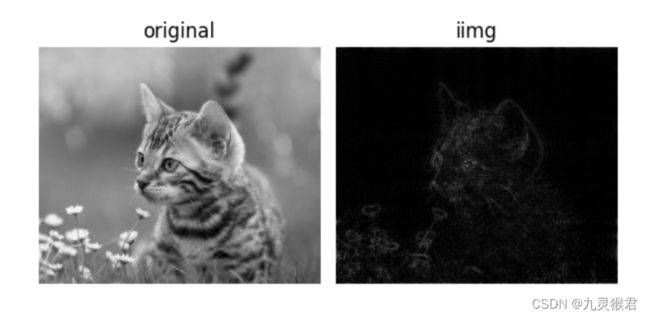
# 显示原始图像和高通滤波处理图像
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('original')
plt.axis('off')
plt.subplot(122), plt.imshow(iimg, 'gray'), plt.title('iimg')
plt.axis('off')
plt.show()
傅里叶变换通过波形来区分图像像素变换的强弱,从而来对图像进行操作。当频域滤波为高通滤波器的时候,就可以实现对图像边缘的提取或锐化。
点击下载源码