HDU3572 :Task Schedule

题目: Our geometry princess XMM has stoped her study in computational geometry to concentrate on her newly opened factory. Her factory has introduced M new machines in order to process the coming N tasks. For the i-th task, the factory has to start processing it at or after day Si, process it for Pi days, and finish the task before or at day Ei. A machine can only work on one task at a time, and each task can be processed by at most one machine at a time. However, a task can be interrupted and processed on different machines on different days.
Now she wonders whether he has a feasible schedule to finish all the tasks in time. She turns to you for help.

Input:On the first line comes an integer T(T<=20), indicating the number of test cases.You are given two integer N(N<=500) and M(M<=200) on the first line of each test case. Then on each of next N lines are three integers Pi, Si and Ei (1<=Pi, Si, Ei<=500), which have the meaning described in the description. It is guaranteed that in a feasible schedule every task that can be finished will be done before or at its end day.

output:For each test case, print “Case x: ” first, where x is the case number. If there exists a feasible schedule to finish all the tasks, print “Yes”, otherwise print “No”.
Print a blank line after each test case.

Sample Input
4 3
1 3 5
1 1 4
2 3 7
3 5 9

2 2
2 1 3
1 2 2

Sample Output
Case 1: Yes

Case 2: Yes

题目描述:有 N个任务,M台机器，每个任务有一个开始时间 S 和截止时间 E 以及需要完成的时间P（需要P天才能完成），一个机器一次只能执行一个任务，一个任务一次也只能 在一台机器上执行，但完成一个任务可分多次在不同的时间（在不同天数），不同的机器上执行。问有没有能给定完成任务的机器工作安排方案。

分析:主要是如何建图。将每个任务抽象成编号1到N的点。与源点S建权值为P的边(表示每个任务需要P天完成)，再将每个任务与该任务可以开始执行的日期(从S 到 E 中间每一个值 i,抽象为点N+i)建权值为1的边 (在这天执行这个任务一天)。最后需要一个总汇点 (max(E)+N+1)，与前面所有任务可执行天数建权值为m的边。

如下图 为第一个样例的图(手残画图,看得懂就行)

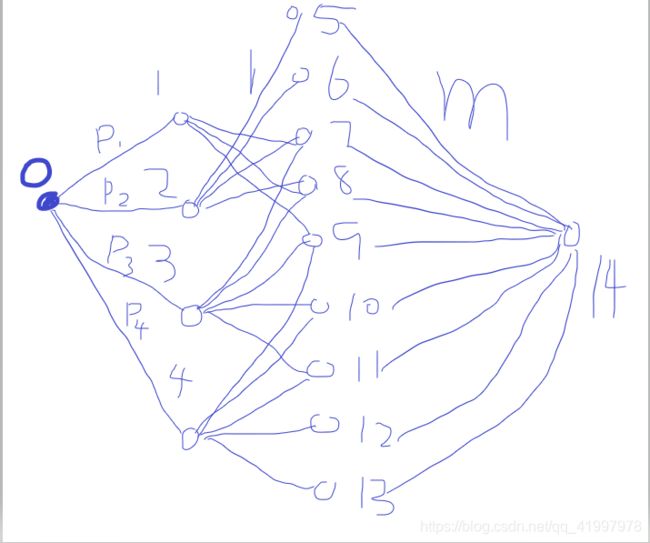
到这一步就很清晰了。每一天都有机器可以执行任务(从5到13)。从0点流入，最终流向14号点的一条增广路径， 表示的是一次机器工作的合法安排。如在5号点流向14号点。最大不能超过m表示这一天工作的机器不能超过m个。如果从0号点经5号点能流通到14号点，则表示5号点表示的这一天机器安排是合法的(不会同时使用超过m台机器)。1号点最大可增广流的值为1号任务可执行的最大次数(这个值不超过P因为只需要P次1号任务就完成了),2,3,4号点同理。
0号点的增广流的值为执行所有任务最大次数(执行一天算一次，总共只需要执行p1+p2+…+pn次所有任务就执行完了).

因此只要判断0号点最大流的值是否等于p1+p2+…+pn（判断是否可以满流）。这题就解决了。

下面给出我写的两个算法(ISAP和dinic)代码:

dinic:

#include
using namespace std;
#include
#include
#include
#define INF 0x3f3f3f3f
struct EDG
{
 int v,w,nxt;
};
int cnt;
int head[2000];
EDG edg[1000000];
int deep[2000];
int T,N,M;
void init()
{
 cnt=0;
 memset(head,-1,sizeof(head));
}
void addedg(int x,int y,int w)
{
 edg[cnt].v=y;
 edg[cnt].w=w;
 edg[cnt].nxt=head[x];
 head[x]=cnt++;
}
int bfs(int s,int t)
{
 queue<int> pq;
 memset(deep,0,sizeof(deep));
 pq.push(s);
 deep[s]=1;
 int top;
 while(!pq.empty())
 {
  top=pq.front();
  pq.pop();
  for(int i=head[top];i+1;i=edg[i].nxt)
  {
   int v=edg[i].v;
   int w=edg[i].w;
   if(!deep[v]&&w)
   {
    deep[v]=deep[top]+1;
    pq.push(v);
   }
  }
 }
 return deep[t];
}
int dfs(int s,int t,int inflow)
{
 if(s==t)
  return inflow;
 int acflow=0;
 for(int i=head[s];i+1;i=edg[i].nxt)
 {
  if(edg[i].w&&deep[s]+1==deep[edg[i].v])
  {
   int x=dfs(edg[i].v,t,min(inflow,edg[i].w));
   if(x>0)
   {
    acflow+=x;inflow-=x;edg[i].w-=x;edg[i^1].w+=x;
    if(!inflow)
     break;
   }
  }
 }
 if(!acflow)
  deep[s]=-2;
 return acflow;
}
int dinic(int s,int t)
{
 int f=0;
 while(bfs(s,t))
  f+=dfs(s,t,INF);
 return f;
}
int main()
{
 scanf("%d",&T);
 for(int i=1;i<=T;i++)
 {
  init();
  scanf("%d%d",&N,&M);
  int P,S,E;
  int et=0,sump=0;
  int tl=INF,tr=0;
  for(int k=1;k<=N;k++)
  {
   scanf("%d%d%d",&P,&S,&E);
   sump+=P;
   if(tl>S)
    tl=S;
   if(E>tr)
    tr=E;
   addedg(0,k,P);
   addedg(k,0,0);
   for(int j=S;j<=E;j++)
   {
    addedg(k,j+N,1);
    addedg(j+N,k,0);
   }
  }
  et=tr+N+1;
  for(int j=tl;j<=tr;j++)
  { 
   addedg(j+N,et,M);
   addedg(et,j+N,0);
  }
  printf("Case %d: %s\n\n",i,dinic(0,et)==sump?"Yes":"No");
 }
 return 0;
}

ISAP:

#include
using namespace std;
#include
#include
#include
#define INF 0x3f3f3f3f
struct EDG
{
 int v,w,nxt;
};
int cnt;
int head[2000];
EDG edg[1000000];
int deep[2000];
int gap[2000];
int T,N,M;
void init()
{
 cnt=0;
 memset(head,-1,sizeof(head));
}
void addedg(int x,int y,int w)
{
 edg[cnt].v=y;
 edg[cnt].w=w;
 edg[cnt].nxt=head[x];
 head[x]=cnt++;
}
void bfs(int s,int t)
{
 queue<int> pq;
 memset(deep,0,sizeof(deep));
 memset(gap,0,sizeof(gap));
 pq.push(t);
 deep[t]=1;
 gap[deep[t]]++;
 int top;
 while(!pq.empty())
 {
  top=pq.front();
  pq.pop();
  for(int i=head[top];i+1;i=edg[i].nxt)
  {
   int v=edg[i].v;
   int w=edg[i].w;
   if(!deep[v]&&!w)
   {
    deep[v]=deep[top]+1;
    gap[deep[v]]++;
    pq.push(v);
   }
  }
 }
}
int dfs(int s,int t,int inflow)
{
 if(s==t)
  return inflow;
 int acflow=0;
 int f=0;
 for(int i=head[s];i+1;i=edg[i].nxt)
 {
  if(edg[i].w>0&&deep[s]==deep[edg[i].v]+1)
  {
   f=1;
   int x=dfs(edg[i].v,t,min(inflow,edg[i].w));
   acflow+=x;inflow-=x;edg[i].w-=x;edg[i^1].w+=x;
   if(!inflow)
    break;
  }
 }
 if(!f)
 {
  gap[deep[s]]--;
  if(gap[deep[s]]==0)
   deep[0]=INF;
  else
  {
   deep[s]++;
   gap[deep[s]]++;
  }
 }
 return acflow;
}
int ISAP(int s,int t)
{
 bfs(s,t);
 int f=0;
 while(deep[0]<INF)
  f+=dfs(s,t,INF);
 return f;
}
int main()
{
 scanf("%d",&T);
 for(int i=1;i<=T;i++)
 {
  init();
  scanf("%d%d",&N,&M);
  int P,S,E;
  int et=0,sump=0;
  int tl=INF,tr;
  for(int k=1;k<=N;k++)
  {
   scanf("%d%d%d",&P,&S,&E);
   sump+=P;
   if(E>et)
    et=E;
   if(tl>S)
    tl=S;
   addedg(0,k,P);
   addedg(k,0,0);
   for(int j=S;j<=E;j++)
   {
    addedg(k,j+N,1);
    addedg(j+N,k,0);
   }
  }
  tr=et;
  et=et+N+1;
  for(int j=tl;j<=tr;j++)
  { 
   addedg(j+N,et,M);
   addedg(et,j+N,0);
  }
  printf("Case %d: %s\n\n",i,ISAP(0,et)==sump?"Yes":"No");
 }
}

用ISAP的话最大层次可以设置为INF（或者N+E+2）,加入gap优化能跑出来（156ms）。虽然从建图过程来看我们建的图只有4层(原点到任务点，任务点到可执行天数点，天数点到总汇点)。但是while(deep[0]<=4)的写法是错的(WA了很多发，我也不知道为什么):有清楚的可以评论回复下。

dinic单路增广直接超时，多路增广124ms(多次提交都比ISAP快一点点)。