回归算法优化过程推导
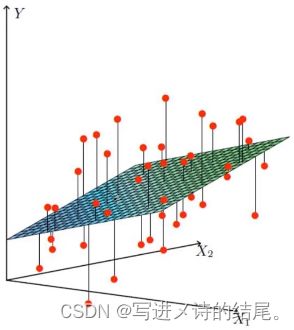
假设存在一个数据集,包含工资、年龄及贷款额度三个维度的数据。我们需要根据这个数据集进行建模,从而在给定工资和年龄的情况下,实现对贷款额度的预测。其中,工资和年龄是模型构建时的两个特征,额度是模型输出的目标值。
| 工资 | 年龄 | 额度 |
|---|---|---|
| 4000 | 25 | 20000 |
| 8000 | 30 | 70000 |
| 5000 | 28 | 35000 |
| 7500 | 33 | 50000 |
| 12000 | 40 | 85000 |
| … | … | … |
我们可以根据数据集和相关需求进行公式建模:
y = θ 0 + θ 1 x 1 + θ 2 x 2 + ε = θ T x + ε y = {\theta }_{0} + {\theta }_{1}x_1 + {\theta }_{2}x_2 + \varepsilon = {\theta }^{T}x + \varepsilon y=θ0+θ1x1+θ2x2+ε=θTx+ε
其中, θ 0 \theta _0 θ0 为偏置项, θ 1 \theta _1 θ1、 θ 2 \theta _2 θ2 为两个特征 x 1 x_1 x1、 x 2 x_2 x2 的权重项, ε \varepsilon ε 为误差项; θ T \theta ^T θT 为一个行向量, x x x 为包含特征 x 1 x_1 x1、 x 2 x_2 x2 的矩阵。
θ 1 x 1 + θ 2 x 2 {\theta }_{1}x_1 + {\theta }_{2}x_2 θ1x1+θ2x2 在三维空间中表示的平面会尽可能去拟合所有数据点(目标值),但是这个平面并不一定是拟合度最高的,也许该平面沿着 y y y 维度向上或向下平移一点距离所得到的新平面才是拟合度最高的,因此我们会在该拟合表达式中加上一个偏置项 θ 0 \theta _0 θ0。
θ 0 + θ 1 x 1 + θ 2 x 2 {\theta }_{0} + {\theta }_{1}x_1 + {\theta }_{2}x_2 θ0+θ1x1+θ2x2 是给定 x 1 x_1 x1、 x 2 x_2 x2 值时,对目标值的预测,预测值与真实值之间必然会存在一个误差,因此我们在该表达式中还需加上一个误差项 ε \varepsilon ε。
对于一个样本而言,公式可以写成如下形式:
y ( i ) = θ T x ( i ) + ε ( i ) ⇒ ε ( i ) = y ( i ) − θ T x ( i ) y^{(i)} = {\theta }^{T}x^{(i)} + \varepsilon ^{(i)} \Rightarrow \varepsilon ^{(i)} = y^{(i)} - {\theta }^{T}x^{(i)} y(i)=θTx(i)+ε(i)⇒ε(i)=y(i)−θTx(i)
其中,每个样本的误差 ε ( i ) \varepsilon ^{(i)} ε(i) 都是独立同分布的,服从均值为 0 0 0 的高斯分布。
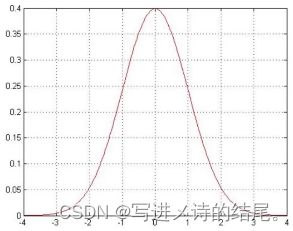
高斯分布的概率密度函数如下所示:
f ( x ) = 1 2 π σ ⋅ e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{(x-\mu )}^{2}}{2{\sigma }^{2}}} f(x)=2πσ1⋅e−2σ2(x−μ)2
把误差带入进去,可得到公式:
f ( ε ( i ) ) = 1 2 π σ ⋅ e − ( ε ( i ) ) 2 2 σ 2 = 1 2 π σ ⋅ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 f({\varepsilon }^{(i)}) = \frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{({\varepsilon }^{(i)})}^{2}}{2{\sigma }^{2}}} = \frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2}}{2{\sigma }^{2}}} f(ε(i))=2πσ1⋅e−2σ2(ε(i))2=2πσ1⋅e−2σ2(y(i)−θTx(i))2
该公式表示误差趋于 0 0 0 的概率,或者说预测值 θ T x ( i ) {\theta }^{T}x^{(i)} θTx(i) 趋近于真实值的概率,这个概率自然是越大越好。
我们的最终目的是要求出最合适的 θ 0 \theta _0 θ0、 θ 1 \theta _1 θ1、 θ 2 \theta _2 θ2,而似然函数是统计学中用于估计参数的一个函数。因此在给出观测数据的前提下,我们可以利用似然函数来推断出未知的参数值。
构建的似然函数如下所示:
L ( θ ) = ∏ i = 1 m 1 2 π σ ⋅ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 L(\theta ) = \displaystyle\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2}}{2{\sigma }^{2}}} L(θ)=i=1∏m2πσ1⋅e−2σ2(y(i)−θTx(i))2
其中,在各个样本都符合独立同分布的情况下,联合概率密度就等于各样本概率密度的乘积,因此这里用了累乘。
想在乘法中求解出参数 θ \theta θ,也许是一个比较难的事,但如果能把乘法转换成加法,对于参数的求解可能就容易了许多。鉴于此,我们可以使用对数似然函数来进行参数的求解。
构建的对数似然函数如下所示:
l o g L ( θ ) = l o g ∏ i = 1 m 1 2 π σ ⋅ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 logL(\theta ) = log\displaystyle\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2}}{2{\sigma }^{2}}} logL(θ)=logi=1∏m2πσ1⋅e−2σ2(y(i)−θTx(i))2
将上述公式进行展开化简:
l o g L ( θ ) = ∑ i = 1 m l o g 1 2 π σ ⋅ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 = m l o g 1 2 π σ + ∑ i = 1 m l o g e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 = m l o g 1 2 π σ − 1 σ 2 ⋅ 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 logL(\theta ) = \displaystyle\sum_{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }·{e}^{-\frac{{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2}}{2{\sigma }^{2}}} \\= mlog\frac{1}{\sqrt{2\pi }\sigma } + \displaystyle\sum_{i=1}^{m}log{e}^{-\frac{{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2}}{2{\sigma }^{2}}} \\= mlog\frac{1}{\sqrt{2\pi }\sigma } - \frac{1}{{\sigma }^{2}}·\frac{1}{2}\displaystyle\sum_{i=1}^{m}{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2} logL(θ)=i=1∑mlog2πσ1⋅e−2σ2(y(i)−θTx(i))2=mlog2πσ1+i=1∑mloge−2σ2(y(i)−θTx(i))2=mlog2πσ1−σ21⋅21i=1∑m(y(i)−θTx(i))2
我们要让似然函数越大越好,因此上述公式等价于让下述目标函数的目标值越小越好:
J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 J(\theta ) = \frac{1}{2}\displaystyle\sum_{i=1}^{m}{(y^{(i)} - {\theta }^{T}x^{(i)})}^{2} J(θ)=21i=1∑m(y(i)−θTx(i))2
我们首先对上述目标函数进行展开:
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) = 1 2 ( θ T X T − y T ) ( X θ − y ) = 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) = 1 2 ( 2 X T X θ − X T y − ( y T X ) T ) = X T X θ − X T y J(\theta ) = \frac{1}{2}{(X\theta - y)}^{T}(X\theta - y) \\ = \frac{1}{2}{(\theta ^TX^T - y^T)}(X\theta - y) \\ = \frac{1}{2}(\theta ^TX^TX\theta - \theta ^TX^Ty - y^TX\theta + y^Ty) \\ = \frac{1}{2}(2X^TX\theta - X^Ty - (y^TX)^T) \\ = X^TX\theta - X^Ty J(θ)=21(Xθ−y)T(Xθ−y)=21(θTXT−yT)(Xθ−y)=21(θTXTXθ−θTXTy−yTXθ+yTy)=21(2XTXθ−XTy−(yTX)T)=XTXθ−XTy
根据展开的公式推出参数值:
θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy
通过这种方法可以进行参数值 θ \theta θ 的求解,但是在上式中, X T X X^TX XTX 不一定是可逆的,也就是说不一定能求解出参数值 θ \theta θ。
鉴于上述问题,我们需要考虑使用其他方法来求解合适的 θ \theta θ,而机器学习就是非常好的方法。一个常规的思路是,我们喂给机器一堆数据,然后告诉它该用什么样的方式学习,并让它朝着这个方向去做(目标/损失函数),每一次学习一点,经过多次迭代优化后,最终收敛至一个稳定的状态。
在对目标函数进行求解时,通常会用到梯度下降法来进行优化。梯度下降是一种常用的优化算法,用于求解目标函数的最小值或最大值。它的基本思想是通过迭代的方式,沿着目标函数的负梯度方向逐步更新参数,以逐渐接近最优解。具体来说,对于一个可微的目标函数,我们希望找到使其取得最小值的参数。梯度下降通过以下步骤进行迭代更新:
- 初始化参数:选择初始参数值作为起点
- 计算梯度:计算目标函数关于参数的梯度(导数)
- 更新参数:将当前参数值沿着负梯度方向移动一小步,更新参数值
- 重复步骤 2 和步骤 3,直到满足停止条件(如达到最大迭代次数或梯度变化很小)
梯度方向指示了函数上升最快的方向,而负梯度方向则指示了函数下降最快的方向。因此,通过不断更新参数,梯度下降算法可以朝着函数取得最小值的方向逐渐迭代,最终接近或达到最优解。
梯度下降算法有多种变体,如批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-Batch Gradient Descent),它们在每次更新参数时所使用的样本数量不同。这些变体具有不同的优缺点,适用于不同的问题和数据集规模。
回到上面的问题,此时的目标/损失函数如下所示:
J ( θ ) = 1 2 m ∑ i = 1 m ( y i − θ T x i ) 2 J(\theta ) = \frac{1}{2m}\displaystyle\sum_{i=1}^{m}(y^i - \theta ^Tx^i)^2 J(θ)=2m1i=1∑m(yi−θTxi)2
当使用批量梯度下降时,目标函数关于第 j j j 个参数的梯度可以写成如下形式:
δ J ( θ ) δ θ j = − 1 m ∑ i = 1 m ( y i − θ T x i ) x j i \frac{\delta J(\theta)}{\delta \theta _j} = -\frac{1}{m}\displaystyle\sum_{i=1}^{m}(y^i - \theta ^Tx^i){x}_{j}^{i} δθjδJ(θ)=−m1i=1∑m(yi−θTxi)xji
更新参数后,新的参数可以表示成如下形式:
θ j ′ = θ j + α ⋅ 1 m ∑ i = 1 m ( y i − θ T x i ) x j i {\theta }_{j}^{'} = \theta _j + \alpha · \frac{1}{m}\displaystyle\sum_{i=1}^{m}(y^i - \theta ^Tx^i){x}_{j}^{i} θj′=θj+α⋅m1i=1∑m(yi−θTxi)xji
当使用随机梯度下降时,目标函数关于第 j j j 个参数的梯度可以写成如下形式:
δ J ( θ ) δ θ j = − ( y i − θ T x i ) x j i \frac{\delta J(\theta)}{\delta \theta _j} = -(y^i - \theta ^Tx^i){x}_{j}^{i} δθjδJ(θ)=−(yi−θTxi)xji
更新参数后,新的参数可以表示成如下形式:
θ j ′ = θ j + α ⋅ ( y i − θ T x i ) x j i {\theta }_{j}^{'} = \theta _j + \alpha · (y^i - \theta ^Tx^i){x}_{j}^{i} θj′=θj+α⋅(yi−θTxi)xji
当使用小批量梯度下降时,目标函数关于第 j j j 个参数的梯度可以写成如下形式:
δ J ( θ ) δ θ j = 1 10 ∑ k = i i + 9 ( θ T x k − y k ) x j k \frac{\delta J(\theta)}{\delta \theta _j} = \frac{1}{10}\displaystyle\sum_{k=i}^{i+9}(\theta ^Tx^k - y^k){x}_{j}^{k} δθjδJ(θ)=101k=i∑i+9(θTxk−yk)xjk
更新参数后,新的参数可以表示成如下形式:
θ j ′ = θ j − α ⋅ 1 10 ∑ k = i i + 9 ( θ T x k − y k ) x j k {\theta }_{j}^{'} = \theta _j - \alpha · \frac{1}{10}\displaystyle\sum_{k=i}^{i+9}(\theta ^Tx^k - y^k){x}_{j}^{k} θj′=θj−α⋅101k=i∑i+9(θTxk−yk)xjk
批量梯度下降容易得到最优解,但是由于每次都要考虑所有样本,因此速度很慢;随机梯度下降每次找一个样本,迭代速度快,但不一定每次都朝着收敛的方向前进(存在离群点、噪声点等干扰);小批量梯度下降比较实用,用的也比较多。