FIR数字滤波器的设计

一、目的和要求

1.掌握用窗函数法设计FIR数字滤波器的原理和方法;

2.熟悉线性相位FIR滤波器的幅频特性和相频特性;
3.了解不同窗函数对滤波器性能的影响。

二、原理和内容

       使用MATLAB编写程序,实现FIR数字滤波器的设计。涉及窗函数法和频率采样法设计FTR数字滤波器的方法、线性相位FIR滤波器的幅频特性和相频特性的特点、窗函数选择及其对滤波器性能的影响等知识点。窗函数设计法是一种把一个长序列变成有限长的短序列的设计方法,是在时域进行的。用窗函数法设计FIR数字滤波器时,先根据Wc和N求出相应的的理想滤波器的单位脉冲响应hd (n)。因为hd(n)一般是非因果的,且无限长,物理上是不可实现的。为此可选择适当的窗函数w(n)截取有限长的hd(n), 即h(n)= hd(n)w(n),只要阶数足够长,截取的方法合理,总能够满足频域的要求。
实际中常用的窗函数有矩形(Boxcar)窗、三角(Bartlett)窗、汉宁(Hanning)窗、汉明(Hamming)窗和布莱克曼(Blackman)窗。这些窗函数各有优缺点,所以要根据实际情况合理选择窗函数类型。

1. 窗函数法设计线性相位FR 波器的一般步骤为:
   (1)确定理想滤波器H,(e")的特性
   (2)由Hd (ejw)求出hd（n）

据过渡带宽度和阻带最小衰减,借助窗函数确定窗的形式及N的大小,四选择适当的窗函数,并根据线性相位条件确定菌函数的长度N: 在MTIAB中,由w-boxcar ()(形窗), w-hanning()(宁窗), w-hamming (0) (明窗).
w-Blackman () (布莱克曼宙), w-Kaiser (, beta) (凯塞窗)等函数来实现富 数设计法中所需的窗函数
(4)由h(n)=h(n) (), 0 (5)对h(n)作离散时间傅立叶变换,得到H(e")。
2.在MTLAB中,可以用b-firl(), n, ftype', taper)等函数辅助设计FIR数字滤波器。N代表滤波器阶数; Wn代表滤波器的截止频率(归一化频率),当设计带通和带阻滤波器时, Wn为双元素相量; ftype代表滤波器类型,如, high' i通,' stop'带阻等: taper为窗函数,默认为海明窗,窗函数实现需要用窗函数
10、hamming, hanning chebwin, kaiser产生

三、步骤

在“开始一程序”菜单中,找到MATIAB程序,运行启动;
进入MTLAB后,在Command Window中输入自己编写的主程序,并执行;
记录运行结果图形，作分析对比。
具体步骤如下：
1.用窗函数法设计一线性相位FIR低通滤波器,要求通带截止频率wc=Π/4

(1)选择一个合适的窗函数(如hamming窗),取单位冲击响应h (n)的长度N=15,观察所设计滤波器的幅频特性,分析是否满足设计要求
(2)取N=45,重复上述设计,观察幅频和相频特性的变化,分析长度N变化的影响；
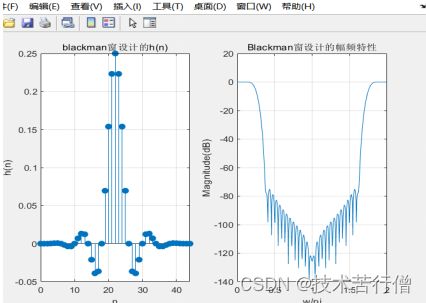
(3)保持N=45不变,改变窗函数(如hamming窗变为blackman窗),观察并记录窗函数对滤波器幅频特性的影响。
2.针对一个含有35Hz、 50Hz和70Hz的混和正弦波信号,设计一个FIR带通滤波器。
参数要求:采样频率fs-400Hz,通带下限截止频率fC1-40Hz,通带上限截止频率fc2-60,过渡带宽8Hz,通阻带波动0.01,采用凯塞窗设计。

四、实验结果与分析

1.

N=15;wc=pi/4;
n=0:N-1;
a=(N-1)/2;
hdn=sin(wc*(n-a))/pi./(n-a);
if rem(N,2)~=0
    hdn(a+1)=wc/pi;
end
wn=hamming(N);
hn=hdn.*wn';
subplot(1,2,1);
stem(n,hn,'');
xlabel('n');ylabel('h(n)');
title('hamming窗设计的h(n)');
grid on;
subplot(1,2,2);
hw=fft(hn,512);
w=2*[0:511]/512;
plot(w,20*log10(abs(hw)));
xlabel('w/pi');ylabel('Magnitude(dB)');
title('hamming窗设计的幅频特性');
grid on;
figure(2)
N=45;wc=pi/4;
n=0:N-1;
a=(N-1)/2;
hdn=sin(wc*(n-a))/pi./(n-a);
if rem(N,2)~=0
    hdn(a+1)=wc/pi;
end
wn=hamming(N);
hn=hdn.*wn';
subplot(1,2,1);
stem(n,hn,'');
xlabel('n');ylabel('h(n)');
title('hamming窗设计的h(n)');
grid on;
subplot(1,2,2);
hw=fft(hn,512);
w=2*[0:511]/512;
plot(w,20*log10(abs(hw)));
xlabel('w/pi');ylabel('Magnitude(dB)');
title('hamming窗设计的幅频特性');
grid on;
figure(3)
N=45;wc=pi/4;
n=0:N-1;
a=(N-1)/2;
hdn=sin(wc*(n-a))/pi./(n-a);
if rem(N,2)~=0
    hdn(a+1)=wc/pi;
end
wn=blackman(N);
hn=hdn.*wn';
subplot(1,2,1);
stem(n,hn,'');
xlabel('n');ylabel('h(n)');
title('blackman窗设计的h(n)');
grid on;
subplot(1,2,2);
hw=fft(hn,512);
w=2*[0:511]/512;
plot(w,20*log10(abs(hw)));
xlabel('w/pi');ylabel('Magnitude(dB)');
title('Blackman窗设计的幅频特性');
grid on;

2.

fc1=40;fc2=60;fs=400;
[n,Wn,beta,ftype]=kaiserord([32 40 60 68],[0 1 0], [0.01 0.01 0.01],400);
window=kaiser(n+1,beta);
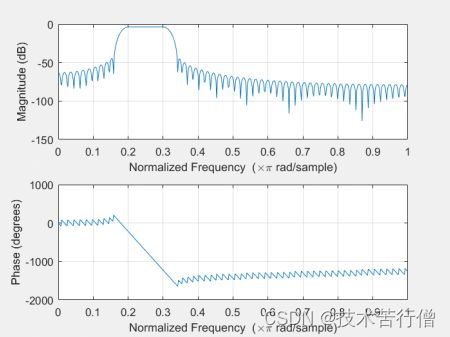
b=fir1(n,Wn,window);
freqz(b,1.512);
t=(0:400)/fs;
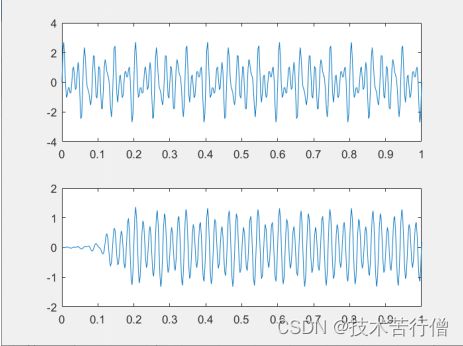
s=sin(2*pi*t*35)+sin(2*pi*t*50)+sin(2*pi*t*70);
sf=filter(b,1,s);
figure
subplot(2,1,1);plot(t,s)
subplot(2,1,2);plot(t,sf)