有限元-二维有限元编程(矩形区域、三角剖分)
有限元-矩形区域三角剖分程序
本文将介绍矩形区域上Poisson方程 − Δ u = f , Δ = ∂ ∂ x 2 + ∂ ∂ y 2 -\Delta u=f,\Delta= \frac{\partial}{\partial x^2}+\frac{\partial}{\partial y^2} −Δu=f,Δ=∂x2∂+∂y2∂的有限元程序编写,包括主要包括三角网格剖分,基函数构造以及函数在任意三角区域二重积分的计算。进一步构造基函数的相关偏导数,荷载向量,刚度矩阵以及替换边界值。
为了使过程清晰,每一部分的详细单独写了分析过程。
理论部分
对于在区域 Ω \Omega Ω上Poisson问题: − Δ u = f , Δ = ∂ ∂ x 2 + ∂ ∂ y 2 -\Delta u=f,\Delta= \frac{\partial}{\partial x^2}+\frac{\partial}{\partial y^2} −Δu=f,Δ=∂x2∂+∂y2∂其中 u u u满足如下边值条件: u ∣ ∂ Ω = α ( x , y ) u|_{\partial \Omega}=\alpha(x,y) u∣∂Ω=α(x,y),它等价的变分形式为:求 u ∈ H 1 ( Ω ) , u ∣ ∂ Ω = α ( x , y ) u\in H^1(\Omega),u|_{\partial \Omega}=\alpha(x,y) u∈H1(Ω),u∣∂Ω=α(x,y),使 a ( u , v ) = ( f , v ) a(u,v)=(f,v) a(u,v)=(f,v),对任意 v ∈ H 0 1 ( Ω ) v\in H_0^1(\Omega) v∈H01(Ω)成立,其中 a ( u , v ) = ∬ Ω ( ∂ u ∂ x ∂ v ∂ x + ∂ u ∂ y ∂ v ∂ y ) d x d y a(u,v) = \iint_{\Omega}(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y})dxdy a(u,v)=∬Ω(∂x∂u∂x∂v+∂y∂u∂y∂v)dxdy, ( f , v ) = ∬ Ω f v d x d y (f,v) = \iint_{\Omega}fvdxdy (f,v)=∬Ωfvdxdy。
过程:将区域 Ω \Omega Ω剖分为 N E NE NE个小三角形,即节点个数为 N P NP NP,则有
a ( u , v ) = ∬ Ω ( ∂ u ∂ x ∂ v ∂ x + ∂ u ∂ y ∂ v ∂ y ) d x d y = ∑ l = 1 N E ∬ e l ( ∂ u ∂ x ∂ v ∂ x + ∂ u ∂ y ∂ v ∂ y ) d x d y a(u,v) = \iint_{\Omega}(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y})dxdy\\\ \ \ \ \ \ \ \ \ \ \ =\sum_{l=1}^{NE}\iint_{e_l}(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y})dxdy a(u,v)=∬Ω(∂x∂u∂x∂v+∂y∂u∂y∂v)dxdy =∑l=1NE∬el(∂x∂u∂x∂v+∂y∂u∂y∂v)dxdy
( f , v ) = ∬ Ω f v d x d y (f,v) = \iint_{\Omega}fvdxdy (f,v)=∬Ωfvdxdy
单元刚度矩阵:
在单元 e l e_l el上,有 u ( x , y ) ≈ u i K i ( x , y ) + u j K j ( x , y ) + u m K m ( x , y ) u(x,y) \approx u_iK_i(x,y)+u_jK_j(x,y)+u_mK_m(x,y) u(x,y)≈uiKi(x,y)+ujKj(x,y)+umKm(x,y),同样,可以使用如上基函数对 v ( x , y ) v(x,y) v(x,y)逼近,即
v ( x , y ) ≈ v i K i ( x , y ) + v j K j ( x , y ) + v m K m ( x , y ) v(x,y) \approx v_iK_i(x,y)+v_jK_j(x,y)+v_mK_m(x,y) v(x,y)≈viKi(x,y)+vjKj(x,y)+vmKm(x,y)
其中, u i , v i u_i,v_i ui,vi分别是函数 u ( ⋅ , ⋅ ) u(\cdot,\cdot) u(⋅,⋅)和 v ( ⋅ , ⋅ ) v(\cdot,\cdot) v(⋅,⋅)在 x i , y i x_i,y_i xi,yi处的取值, u j , u m u_j,u_m uj,um类似。需要注意到点 ( x i , y i ) , ( x j , y j ) (x_i,y_i),(x_j,y_j) (xi,yi),(xj,yj)和 ( x m , y m ) (x_m,y_m) (xm,ym)是三角单元 e l e_l el的顶点。
因此
∬ e l ( ∂ u ∂ x ∂ v ∂ x + ∂ u ∂ y ∂ v ∂ y ) d x d y = ∬ e l [ v i v j v m ] [ k i i k i j k i m k j i k j j k j m k m i k m j k m m ] [ u i u j u m ] d x d y \iint_{e_l}(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y})dxdy\\=\iint_{e_l}\begin{bmatrix}v_i&v_j&v_m \end{bmatrix}\begin{bmatrix}k_{ii}&k_{ij}&k_{im} \\k_{ji}&k_{jj}&k_{jm} \\k_{mi}&k_{mj}&k_{mm} \end{bmatrix}\begin{bmatrix}u_i\\u_j\\u_m \end{bmatrix}dxdy ∬el(∂x∂u∂x∂v+∂y∂u∂y∂v)dxdy=∬el[vivjvm] kiikjikmikijkjjkmjkimkjmkmm uiujum dxdy
其中 k s t = ( ∂ K s ∂ x ∂ K s ∂ x + ∂ K t ∂ y ∂ K t ∂ y ) , s , t = i , j , m k_{st}=(\frac{\partial K_s}{\partial x}\frac{\partial K_s}{\partial x}+\frac{\partial K_t}{\partial y}\frac{\partial K_t}{\partial y}),\ \ \ \ \ \ s,t=i,j,m kst=(∂x∂Ks∂x∂Ks+∂y∂Kt∂y∂Kt), s,t=i,j,m
记矩阵 [ K e ] = ∬ e [ k i i k i j k i m k j i k j j k j m k m i k m j k m m ] d x d y [K_e]=\iint_{e}\begin{bmatrix}k_{ii}&k_{ij}&k_{im} \\k_{ji}&k_{jj}&k_{jm} \\k_{mi}&k_{mj}&k_{mm} \end{bmatrix}dxdy [Ke]=∬e kiikjikmikijkjjkmjkimkjmkmm dxdy为单元刚度矩阵。
单位荷载向量:
同理可得 ( f , v ) = ∬ e l f v d x d y = ∬ e l [ v i v j v m ] [ K i K j K m ] f ( x , y ) d x d y (f,v) = \iint_{e_l}fvdxdy\\\ \ \ \ \ \ \ \ \ \ \ =\iint_{e_l}\begin{bmatrix}v_i&v_j&v_m \end{bmatrix}\begin{bmatrix}K_{i}\\K_{j}\\K_{m}\end{bmatrix}f(x,y)dxdy (f,v)=∬elfvdxdy =∬el[vivjvm] KiKjKm f(x,y)dxdy,
记向量 { F e } = ∬ e [ K i K j K m ] f ( x , y ) d x d y \{F_e\}=\iint_{e}\begin{bmatrix}K_{i}\\K_{j}\\K_{m}\end{bmatrix}f(x,y)dxdy {Fe}=∬e KiKjKm f(x,y)dxdy
对于不同的单元 e l , l = 1 , 2 , 3... N E e_l,l=1,2,3...NE el,l=1,2,3...NE来说,其对应的 i , j , m i,j,m i,j,m是不一样的,因此,为使在不同单元上的单元刚度矩阵和单元荷载能够求和,将单位刚度矩阵和单位荷载向量分别扩充为 N P × N P NP\times NP NP×NP的矩阵和 N P × 1 NP\times 1 NP×1的向量,如下:
[ K e ] ˉ = ∬ e [ ⋮ ⋮ ⋮ ⋯ k i i ⋯ k i j ⋯ k i m ⋯ ⋮ ⋮ ⋮ ⋯ k j i ⋯ k j j ⋯ k j m ⋯ ⋮ ⋮ ⋮ ⋯ k m i ⋯ k m j ⋯ k m m ⋯ ⋮ ⋮ ⋮ ] d x d y \bar{[K_e]}=\iint_{e}\begin{bmatrix} & \vdots& &\vdots & &\vdots & \\ \cdots& k_{ii}&\cdots&k_{ij}&\cdots&k_{im}&\cdots \\ & \vdots& &\vdots & &\vdots & \\ \cdots&k_{ji}&\cdots&k_{jj}&\cdots&k_{jm}&\cdots \\ & \vdots& &\vdots & &\vdots & \\ \cdots&k_{mi}&\cdots&k_{mj}&\cdots&k_{mm}&\cdots \\ & \vdots& &\vdots & &\vdots &\end{bmatrix}dxdy [Ke]ˉ=∬e ⋯⋯⋯⋮kii⋮kji⋮kmi⋮⋯⋯⋯⋮kij⋮kjj⋮kmj⋮⋯⋯⋯⋮kim⋮kjm⋮kmm⋮⋯⋯⋯ dxdy
{ F e } ˉ = ∬ e [ ⋮ K i ⋮ K j ⋮ K m ⋮ ] f ( x , y ) d x d y \bar{\{F_e\}}=\iint_{e}\begin{bmatrix}\vdots\\K_{i}\\\vdots\\K_{j}\\\vdots\\K_{m}\\\vdots\end{bmatrix}f(x,y)dxdy {Fe}ˉ=∬e ⋮Ki⋮Kj⋮Km⋮ f(x,y)dxdy
上面两个矩阵中,其中虚点表达0元素,也就是在矩阵 [ K e ] ˉ \bar{[K_e]} [Ke]ˉ中至多有九个非零元,非零元的位置如上;在 { F e } ˉ \bar{\{F_e\}} {Fe}ˉ中至多有三个非零元,非零元的位置如上。记 U = [ u 1 u 2 ⋮ u N P ] U = \begin{bmatrix} u_1\\u_2\\\vdots\\u_{NP}\end{bmatrix} U= u1u2⋮uNP , V = [ v 1 v 2 ⋮ v N P ] V = \begin{bmatrix} v_1\\v_2\\\vdots\\v_{NP}\end{bmatrix} V= v1v2⋮vNP
记 K ˉ = ∑ l N E [ K e l ] ˉ \bar K=\sum_l^{NE}\bar{[K_{e_l}]} Kˉ=∑lNE[Kel]ˉ, F ˉ = ∑ l N E { F e l } ˉ \bar F=\sum_l^{NE}\bar{\{F_{e_l}\}} Fˉ=∑lNE{Fel}ˉ
则 a ( u , v ) = ( f , v ) a(u,v)=(f,v) a(u,v)=(f,v)近似于 V T K ˉ U = V T F ˉ V^T\bar{K}U=V^T\bar{F} VTKˉU=VTFˉ,即 V T ( K ˉ U − K ˉ ) = 0 V^T(\bar{K}U-\bar{K})=0 VT(KˉU−Kˉ)=0,由于 v ( x , y ) v(x,y) v(x,y)的任意性,因此对于任意的 V V V, V T ( K ˉ U − F ˉ ) = 0 V^T(\bar{K}U-\bar{F})=0 VT(KˉU−Fˉ)=0总是成立的,故 K ˉ U − F ˉ = 0 \bar{K}U-\bar{F}=0 KˉU−Fˉ=0。
理论可能写的不够详细,感觉有点乱,见谅。
网格剖分
在有限元-区域划分博客中,已经着重介绍了矩形区域上三角网格的剖分,包括保存节点位置的矩阵 P o s Pos Pos和保存三角形顶点位置的连接矩阵 T T T,将其封装为函数,如下
function [pos,T] = FE_grid(X,Y,nx,ny)
% 三角网格划分
% 输入参数区间X,区间Y,nx为X中划分的区间个数,ny为Y中划分的区间个数;
% 输出参数pos为节点位置,T为三角网格划分后三角形的三个节点位置(连接矩阵,维度3*N);
% 该矩阵每一列从上到下为逆时针节点位置;
% lenx与leny分别为X与Y划分后的节点数量;
hx = (X(2)-X(1))/nx;
hy = (Y(2)-Y(1))/ny;
x = X(1):hx:X(2);
y = Y(1):hy:Y(2);
lenx = length(x);
leny = length(y);
pos = zeros(2,lenx*leny);
for i = 1:leny
pos(1,(1 + (i-1)*lenx):i*(lenx)) = x;
pos(2,(1 + (i-1)*lenx):i*(lenx)) = y(i);
end
T = zeros(3,2*(lenx-1)*(leny-1));
for i = 1:(lenx-1)*(leny-1)
row = ceil(i/(lenx-1))-1;
list = i - row * (lenx - 1);
% 第 i 个正方形的四个顶点为 x_row x_(row+1) y_list y_(list+1)
% 根据这四个顶点信息,我们可以构造不同形状的三角网格。
T(1,2*i-1) = row * lenx + list;
T(2,2*i-1) = (row + 1) * lenx + (list + 1);
T(3,2*i-1) = (row + 1) * lenx + list;
T(1,2*i) = row * lenx + list;
T(2,2*i) = row * lenx + (list + 1);
T(3,2*i) = (row + 1) * lenx + (list + 1);
end
基函数构造
在线性插值函数的基函数构造博客中,已经着重介绍了如何构造过不在同一直线上的三个点的平面,以及整理后得到的线性插值的基函数,这里将其封装,通过输入三个不在同一直线上的节点,返回三个插值基函数,具体函数如下:
function func = basis_function_2D(e_pos)
% 构造2D插值基函数,
% 即F(t,s) = f1*K1(t,s) + f2*K2(t,s) + f3*K3(t,s),
% 返回一个1*3的元胞数组,元素分别为3个基函数(K1,K2,K3)。
p = (e_pos(1,2)-e_pos(1,1))*(e_pos(2,3)-e_pos(2,1)) - (e_pos(2,2)-e_pos(2,1))*(e_pos(1,3)-e_pos(1,1));
% K1 = @(t,s)((e_pos(2,2)-e_pos(2,3))*t - (e_pos(1,2)-e_pos(1,3))*s + e_pos(1,2)*e_pos(2,3)-e_pos(1,3)*e_pos(2,2))/p;
% K2 = @(t,s)((e_pos(2,3)-e_pos(2,1))*t - (e_pos(1,3)-e_pos(1,1))*s + e_pos(1,3)*e_pos(2,1)-e_pos(1,1)*e_pos(2,3))/p;
% K3 = @(t,s)((e_pos(2,1)-e_pos(2,2))*t - (e_pos(1,1)-e_pos(1,2))*s + e_pos(1,1)*e_pos(2,2)-e_pos(1,2)*e_pos(2,1))/p;
% 上面和下面的基函数写法都是正确的。
K1 = @(t,s)((s-e_pos(2,2)).*(e_pos(1,3)-e_pos(1,2)) - (t-e_pos(1,2)).*(e_pos(2,3)-e_pos(2,2)))/p;
K2 = @(t,s)((s-e_pos(2,3)).*(e_pos(1,1)-e_pos(1,3)) - (t-e_pos(1,3)).*(e_pos(2,1)-e_pos(2,3)))/p;
K3 = @(t,s)((s-e_pos(2,1)).*(e_pos(1,2)-e_pos(1,1)) - (t-e_pos(1,1)).*(e_pos(2,2)-e_pos(2,1)))/p;
func = cell(1,3);
func{1} = K1;
func{2} = K2;
func{3} = K3;
end
函数在任意三角区域二重积分的计算
在函数在任意三角区域二重积分的计算博客中,已经着重介绍了任意三角区域二重积分的计算,在下面这个函数中,你只需要输入三角形三个顶点对应坐标以及函数 f 1 ( x , y ) f1(x,y) f1(x,y),就可以得到函数 f 1 ( x , y ) f1(x,y) f1(x,y)在这三个点确定的三角区域上的二重积分值。
function I = triangle_integral(point,f1)
% 该函数用于求三角区域上函数的积分
x = point(1,:);
y = point(2,:);
X = x(2:3) - x(1);
Y = y(2:3) - y(1);
if X(1)>0
sita = pi/2-atan(Y(1)/X(1));
elseif X(1)<0
sita = -pi/2-atan(Y(1)/X(1));
else
if Y(1)>0
sita = 0;
else
sita = pi;
end
end
A = [cos(sita) -sin(sita)
sin(sita) cos(sita)];
P =A*([x;y]-[x(1);y(1)])+[x(1);y(1)];
xp = P(1,:);
yp = P(2,:);
fun = @(t,s) f1(cos(sita)*(t-x(1))+sin(sita)*(s-y(1))+x(1),-sin(sita)*(t-x(1))+cos(sita)*(s-y(1))+y(1));
% 下面描述积分区域边界
% 旋转变换以A为旋转点,旋转三角形ABC,使得边(AB)与y轴平行且Ay
% 从而,积分区间可以描述:y方向,下边界为边(AC),上边界为边(BC)
% x方向上为常数值,左端点为 min(P(1,:)),右端点为 max(P(1,:))
% A,B,C三点分别为P(:,1),P(:,2),P(:,3)
y_down = @(t) (yp(3)-yp(1))/(xp(3)-xp(1)).*(t-xp(1)) + yp(1);
y_up = @(t) (yp(3)-yp(2))/(xp(3)-xp(2)).*(t-xp(2)) + yp(2);
I = integral2(fun,min(xp),max(xp),y_down,y_up);
基函数偏导数的构造:
这个比较简单,因为基函数的具体形式已经给出,所以这里我们直接给出基函数偏导数的代码:
function [dx,dy] = diff_basis_fun(e_pos)
% 构造插值基函数的偏导数分别为K1x,K1y,K2x,K2y,K3x,K3y
% 注意到每个函数中都有(t-t+s-s)这样的一个和式,这并不影响函数本身的值
% 但在使用过程中,他将产生和输入一样维数的输出
p = (e_pos(1,2)-e_pos(1,1))*(e_pos(2,3)-e_pos(2,1)) - (e_pos(2,2)-e_pos(2,1))*(e_pos(1,3)-e_pos(1,1));
K1x =@(t,s)t-t+s-s+(e_pos(2,2)-e_pos(2,3))/p;
K2x =@(t,s)t-t+s-s+(e_pos(2,3)-e_pos(2,1))/p;
K3x =@(t,s)t-t+s-s+(e_pos(2,1)-e_pos(2,2))/p;
K1y =@(t,s)t-t+s-s+(e_pos(1,3)-e_pos(1,2))/p;
K2y =@(t,s)t-t+s-s+(e_pos(1,1)-e_pos(1,3))/p;
K3y =@(t,s)t-t+s-s+(e_pos(1,2)-e_pos(1,1))/p;
dx = cell(1,3);
dy = cell(1,3);
dx{1} = K1x;
dx{2} = K2x;
dx{3} = K3x;
dy{1} = K1y;
dy{2} = K2y;
dy{3} = K3y;
end
荷载向量的构造
根据理论知识可以构造荷载向量,代码如下:
F = zeros(p_b,1);
for i = 1:e_b
e_pos = pos(:,T(:,i));
b_func = basis_function_2D(e_pos);
for j = 1:3
b_f = b_func{j};
b_f = @(t,s) b_f(t,s).*f(t,s);
F(T(j,i)) = F(T(j,i)) + triangle_integral(e_pos,b_f);
end
end
刚度矩阵的构造
刚度矩阵的构造同理:
A = sparse(p_b,p_b);
for i = 1:e_b
e_pos = pos(:,T(:,i));
[funcx,funcy]= diff_basis_fun(e_pos);
for j = 1:3
b_fx1 = funcx{j};
b_fy1 = funcy{j};
for k = 1:3
b_fx2 = funcx{k};
b_fy2 = funcy{k};
% Laplace算子
La_f =@(t,s) b_fx1(t,s).*b_fx2(t,s) + b_fy1(t,s).*b_fy2(t,s);
A = A + sparse(T(k,i),T(j,i),triangle_integral(e_pos,La_f),p_b,p_b);
end
end
end
边界值的替换
最后处理边界点,首先找到边界点的对应的位置,将刚度矩阵中对应行替换为向量 ( 0 , 0 , . . . 0 , 1 , 0 , . . . 0 ) (0,0,...0,1,0,...0) (0,0,...0,1,0,...0),向量中1的位置为边界点对应在向量U中的位置,由于边界值是已知的,进一步替换荷载向量对应位置为所取边界值。
实例:
实例1:
这个实例是博客有限元方法入门:有限元方法简单的二维算例(三角形剖分)中使用的例子, − Δ u = f , u ∣ ∂ Ω = 0 -\Delta u=f,u|_{\partial \Omega}=0 −Δu=f,u∣∂Ω=0,其中 Ω = ( 0 , 1 ) 2 \Omega = ( 0 , 1 ) ^2 Ω=(0,1)2且 f = 2 π 2 sin ( π x ) sin ( π y ) f=2\pi^2\sin(\pi x)\sin(\pi y) f=2π2sin(πx)sin(πy),真解为 u ( x , y ) = sin ( π x ) sin ( π y ) u(x,y)=\sin(\pi x)\sin(\pi y) u(x,y)=sin(πx)sin(πy)。
结果如下:
| 数值解 | 误差图 | |
|---|---|---|
| n x = 16 n y = 16 nx =16\\ny=16 nx=16ny=16 | 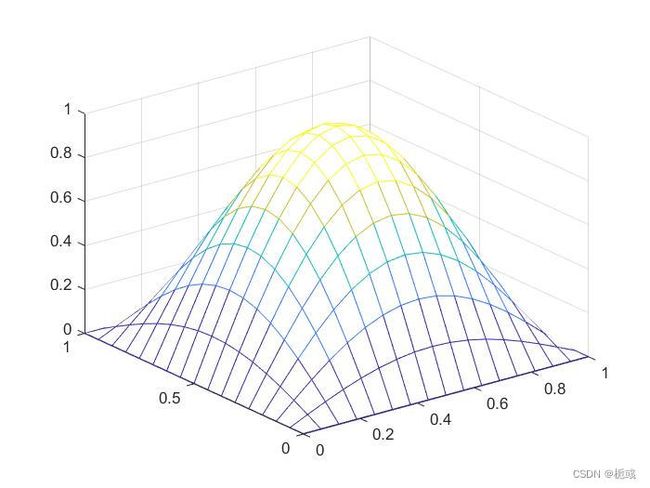 |
 |
| n x = 32 n y = 32 nx =32\\ny=32 nx=32ny=32 |  |
 |
| n x = 64 n y = 64 nx =64\\ny=64 nx=64ny=64 |  |
 |
| n x = 128 n y = 128 nx =128\\ny=128 nx=128ny=128 | 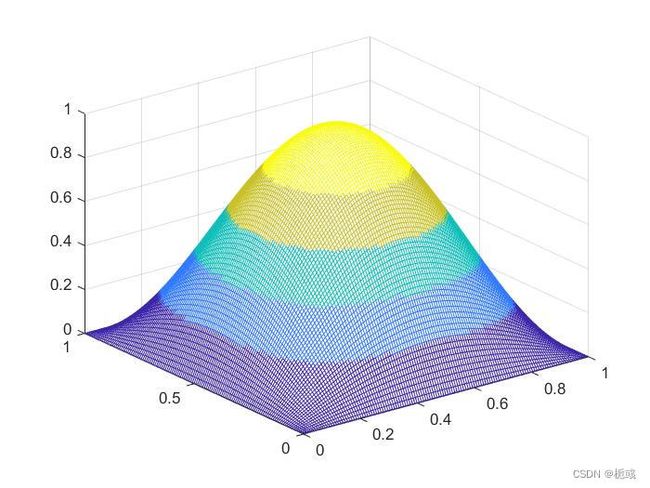 |
 |
实例代码
clc,clear,close all
nx = 128;
ny = 128;
X = [0,1];
Y = [0,1];
hx = (X(2)-X(1))/nx;
hy = (Y(2)-Y(1))/ny;
[pos,T] = FE_grid(X,Y,nx,ny);
[~ ,p_b] = size(pos);
[~ ,e_b] = size(T);
% 构造荷载向量
% 右端函数
f = @(t,s) 2*pi^2*sin(pi*t).*sin(pi*s);
F = zeros(p_b,1);
for i = 1:e_b
e_pos = pos(:,T(:,i));
b_func = basis_function_2D(e_pos);
for j = 1:3
b_f = b_func{j};
b_f = @(t,s) b_f(t,s).*f(t,s);
F(T(j,i)) = F(T(j,i)) + triangle_integral(e_pos,b_f);
end
end
% 构造刚度矩阵
A = sparse(p_b,p_b);
for i = 1:e_b
e_pos = pos(:,T(:,i));
[funcx,funcy]= diff_basis_fun(e_pos);
for j = 1:3
b_fx1 = funcx{j};
b_fy1 = funcy{j};
for k = 1:3
b_fx2 = funcx{k};
b_fy2 = funcy{k};
% Laplace算子
% La_f是刚度矩阵中单元上的求积函数
La_f =@(t,s) b_fx1(t,s).*b_fx2(t,s) + b_fy1(t,s).*b_fy2(t,s);
A = A + sparse(T(k,i),T(j,i),triangle_integral(e_pos,La_f),p_b,p_b);
end
end
end
% 修改边界条件
bound_xl = find(pos(1,:) == X(1));
bound_xr = find(pos(1,:) == X(2));
bound_yd = find(pos(2,:) == Y(1));
bound_yu = find(pos(2,:) == Y(2));
e = eye(p_b);
i_point = intersect(union(bound_yd,bound_yu),union(bound_xr,bound_xl));
A(i_point,:) = e(i_point,:);
% 获取边界点的位置
bound = union(union(bound_yd,bound_yu),union(bound_xr,bound_xl));
e = eye(p_b);
for i = 1:length(bound)
A(bound(i),:) = e(bound(i),:);
F(bound(i)) = 0;
end
u = A\F;
U = zeros(ny+1,nx+1);
for i = 1:(ny+1)
U(i,:) = u((i-1)*(nx+1)+1:i*(nx+1));
end
figure
[gridX,gridY] = meshgrid(X(1):hx:X(2),Y(1):hy:Y(2));
mesh(gridX,gridY,U)
F_k = @(x,y)sin(pi*x).*sin(pi*y);
colormap(parula(5))
figure
mesh(gridX,gridY,F_k(gridX,gridY)-U)
colormap(parula(5))
实例2:
这个例子在《数值方法(MATLAB版)(第四版)》(John H.Mathews与Kurtis D.Fink所著)第402页例10.7,如下:

所得数值解
实例代码如下:
这段代码和上面的代码几乎一样,只是右端函数不同,以及边界处的赋值代码不一样:
clc,clear,close all
nx = 8;
ny = 8;
X = [0,4];
Y = [0,4];
hx = (X(2)-X(1))/nx;
hy = (Y(2)-Y(1))/ny;
[pos,T] = FE_grid(X,Y,nx,ny);
[~ ,p_b] = size(pos);
[~ ,e_b] = size(T);
% 构造荷载向量
% 右端函数
f =@(t,s) 0;
F = zeros(p_b,1);
for i = 1:e_b
e_pos = pos(:,T(:,i));
b_func = basis_function_2D(e_pos);
for j = 1:3
b_f = b_func{j};
b_f = @(t,s) b_f(t,s).*f(t,s);
F(T(j,i)) = F(T(j,i)) + triangle_integral(e_pos,b_f);
end
end
% 构造刚度矩阵
A = sparse(p_b,p_b);
for i = 1:e_b
e_pos = pos(:,T(:,i));
[funcx,funcy]= diff_basis_fun(e_pos);
for j = 1:3
b_fx1 = funcx{j};
b_fy1 = funcy{j};
for k = 1:3
b_fx2 = funcx{k};
b_fy2 = funcy{k};
% Laplace算子
% La_f是刚度矩阵中单元上的求积函数
La_f =@(t,s) b_fx1(t,s).*b_fx2(t,s) + b_fy1(t,s).*b_fy2(t,s);
A = A + sparse(T(k,i),T(j,i),triangle_integral(e_pos,La_f),p_b,p_b);
end
end
end
% 修改边界条件
bound_xl = find(pos(1,:) == X(1));
bound_xr = find(pos(1,:) == X(2));
bound_yd = find(pos(2,:) == Y(1));
bound_yu = find(pos(2,:) == Y(2));
e = eye(p_b);
for i = 1:length(bound_xl)
% 左边界
A(bound_xl(i),:) = e(bound_xl(i),:);
F(bound_xl(i)) = 80;
% 右边界
A(bound_xr(i),:) = e(bound_xr(i),:);
F(bound_xr(i)) = 0;
end
for i = 1: length(bound_yd)
% 下边界
A(bound_yd(i),:) = e(bound_yd(i),:);
F(bound_yd(i)) = 20;
% 上边界
A(bound_yu(i),:) = e(bound_yu(i),:);
F(bound_yu(i)) = 180;
end
i_point = intersect(union(bound_yd,bound_yu),union(bound_xr,bound_xl));
A(i_point,:) = e(i_point,:);
F(i_point) = [50;10;130;90];
% 获取边界点的位置
u = A\F;
U = zeros(ny+1,nx+1);
for i = 1:(ny+1)
U(i,:) = u((i-1)*(nx+1)+1:i*(nx+1));
end
figure
[gridX,gridY] = meshgrid(X(1):hx:X(2),Y(1):hy:Y(2));
surf(gridX,gridY,U)
注意:使用到的函数实例只是验证我们的代码可以求解问题。
