（数学建模）傅里叶变换-第一节——定义和简单例子（Python实现）

一、引入

生活当中，我们常常需要把杂乱的信息分解开进行研究。比如我们看到的光是无色的，但是当其透过三棱镜时，会发生色散，这样不同颜色的光就被我们分离出来了，我们就可以对光进行研究了。光是一种电磁波，同样地，声波、收音机的波也可以进行类似的处理，将不同的频段分离出来，就可以进行降噪。

二、概念

f(t)是t的周期函数，如果t满足狄里赫莱条件：在一个以2T为周期内f(X)连续或只有有限个第一类间断点，附f（x）单调或可划分成有限个单调区间，则F（x）以2T为周期的傅里叶级数收敛，和函数S（x）也是以2T为周期的周期函数，且在这些间断点上，函数是有限值；在一个周期内具有有限个极值点；绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换，
②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的像函数，f(t)叫做
F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像。
①傅立叶变换

②傅立叶逆变换

（以上摘自百度百科词条“傅里叶变换”）

三、代码实现

由上面的定义我们看到，傅里叶变换是可逆的，其允许原始信号和变换过的信号相互转换。但是要注意，在任一时刻只有一种信息可用。即变换后的频域中没有时间信息（如图2），逆变换（也就是变换前）的时域中没有频率信息（如图1）。

图1绘制代码如下：

以信号 y=np.cos(2pa10x)+np.cos(2pa25x)+np.cos(2pa50x)+np.cos(2pa100x)为例（x可以看作时间，单位为秒）（我们将信号y用10、25、50、100Hz的频率加合表示）

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.figure()


import numpy as np
import math
pa=math.pi
x=np.linspace(0,0.5,200)
y=np.cos(2*pa*10*x)+np.cos(2*pa*25*x)+np.cos(2*pa*50*x)+np.cos(2*pa*100*x)
plt.xlabel('Time/s')
plt.plot(x,y,'k-')
plt.show()

显示效果下图：

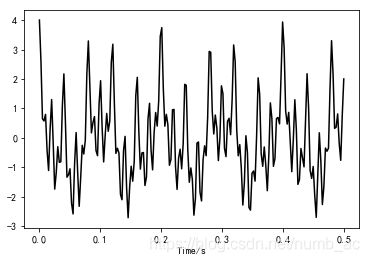
（图1）
然后我们绘制它的傅里叶变换，代码如下：

# -*- coding: utf-8 -*-
"""
Created on Thu Oct 17 15:23:10 2019

@author: abc
"""

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.figure()


import numpy as np
import math
pa=math.pi
tim=1
fft_size=300
x=np.linspace(0,tim,fft_size)                                                       #这里我们将采样点定到200
y=np.cos(2*pa*10*x)+np.cos(2*pa*25*x)+np.cos(2*pa*50*x)+np.cos(2*pa*100*x)

plt.xlabel('Time/s')
plt.plot(x,y,'k-')
plt.show()

ys=y[:fft_size]                                                                     #ys是y的一份复制                                   
yf=np.fft.rfft(ys)/fft_size                                                         
#上面这一行是关键，采用了fft函数进行了快速傅里叶变换的计算,但是此时的yf还不是纵坐标,fft的运算结果为复数。那么它为什么是复数呢？
#从物理意义上来看，傅里叶变换在将信号分解的时候，是将其分为了正弦以及余弦的叠加形式，而决定一个正弦波的是其振幅和相位，二者缺一不可。
#显然，单个实数是无法同时描述振幅和相位的，那么就得用复数来进行表示了。然而，在本节例子中，我们只关心其振幅
#/fft_size是为了正确显示波形能量
yfp=(np.clip(np.abs(yf), 1e-20, 1e100))                                             #这里的clip起到截取的作用，去除yf中非（1e-20, 1e100）范围的点

print(yf)                                                                           #输出fft算出的复数

caiyang_freq=fft_size/tim                                                           #采样频率指的是每秒采多少点，我们这里描述1秒，采了300个点（点数和fft_size一致）
#这里注意采样频率的规则是要大于3~4倍的最高频率分量，以免发生混频现象。本案例最高频率分量为100
freqs=np.linspace(0,caiyang_freq//2, fft_size//2+1)

#pl.subplot(212)
plt.plot(freqs, yfp)
plt.xlabel(u"Freq(Hz)")
#pl.subplots_adjust(hspace=0.4)

plt.show()

mp=np.zeros(shape=(4,fft_size))
mp[0]=np.cos(2*pa*10*x)
mp[1]=np.cos(2*pa*25*x)
mp[2]=np.cos(2*pa*50*x)
mp[3]=np.cos(2*pa*100*x)
color=['k-','b-','g-','r-']
for i in range(4):
  plt.plot(x,mp[i],color[i])
plt.show()
  

输出效果如下：

[ 1.33333333e-02+0.00000000e+00j 1.33728032e-02+1.40044787e-04j
1.34954364e-02+2.82689093e-04j 1.37152571e-02+4.31019319e-04j
1.40610429e-02+5.89332308e-04j 1.45886146e-02+7.64556894e-04j
1.54123961e-02+9.69665772e-04j 1.68001299e-02+1.23372442e-03j
1.95476426e-02+1.64146141e-03j 2.75298954e-02+2.60234131e-03j
5.07907842e-01+5.33832654e-02j -5.44986931e-03-6.30571393e-04j
3.46479316e-03+4.37705167e-04j 6.53563025e-03+8.95269981e-04j
8.22499547e-03+1.21456166e-03j 9.41282144e-03+1.49084445e-03j
1.04041222e-02+1.75972554e-03j 1.13496526e-02+2.04212482e-03j
1.23556537e-02+2.35696699e-03j 1.35314474e-02+2.72841840e-03j
1.50325162e-02+3.19525996e-03j 1.71395501e-02+3.83114335e-03j
2.04762753e-02+4.80266701e-03j 2.68443022e-02+6.59359302e-03j
4.46706970e-02+1.14694856e-02j 4.85304737e-01+1.30037012e-01j
-3.54130614e-02-9.88750441e-03j -1.25352064e-02-3.64181412e-03j
-5.23579845e-03-1.58078075e-03j -1.57424499e-03-4.93338477e-04j
6.77316417e-04+2.20073445e-04j 2.24256720e-03+7.54707243e-04j
3.42872853e-03+1.19400960e-03j 4.39001370e-03+1.58050218e-03j
5.21396288e-03+1.93905541e-03j 5.95574862e-03+2.28619770e-03j
6.65390354e-03+2.63446678e-03j 7.33851510e-03+2.99479254e-03j
8.03617214e-03+3.37809571e-03j 8.77362030e-03+3.79668454e-03j
9.58127136e-03+4.26585685e-03j 1.04975772e-02+4.80616611e-03j
1.15756744e-02+5.44709890e-03j 1.28949348e-02+6.23365503e-03j
1.45832742e-02+7.23920018e-03j 1.68649919e-02+8.59314256e-03j
2.01771818e-02+1.05483757e-02j 2.55063979e-02+1.36764106e-02j
3.56571024e-02+1.96026579e-02j 6.30400753e-02+3.55212569e-02j
4.16907105e-01+2.40701429e-01j -7.88880794e-02-4.66542801e-02j
-3.35724196e-02-2.03321800e-02j -2.02026755e-02-1.25261895e-02j
-1.37758295e-02-8.74240725e-03j -9.98302765e-03-6.48305396e-03j
-7.47006431e-03-4.96309886e-03j -5.67528982e-03-3.85692298e-03j
-4.32370142e-03-3.00505077e-03j -3.26468829e-03-2.32009320e-03j
-2.40878201e-03-1.75008257e-03j -1.69943676e-03-1.26211312e-03j
-1.09911655e-03-8.34274870e-04j -5.81885342e-04-4.51356538e-04j
-1.29209286e-04-1.02410018e-04j 2.72544940e-04+2.20702541e-04j
6.33665761e-04+5.24213907e-04j 9.62099935e-04+8.13037482e-04j
1.26412055e-03+1.09115959e-03j 1.54478480e-03+1.36191100e-03j
1.80825614e-03+1.62816114e-03j 2.05803715e-03+1.89246217e-03j
2.29714233e-03+2.15716023e-03j 2.52823027e-03+2.42448566e-03j
2.75370827e-03+2.69663037e-03j 2.97581864e-03+2.97581864e-03j
3.19671367e-03+3.26437652e-03j 3.41852451e-03+3.56480439e-03j
3.64342889e-03+3.87985770e-03j 3.87372220e-03+4.21264125e-03j
4.11189690e-03+4.56672416e-03j 4.36073637e-03+4.94628449e-03j
4.62343100e-03+5.35629637e-03j 4.90372747e-03+5.80277784e-03j
5.20612682e-03+6.29312628e-03j 5.53615513e-03+6.83658223e-03j
5.90074300e-03+7.44488482e-03j 6.30877203e-03+8.13321989e-03j
6.77188384e-03+8.92162749e-03j 7.30571426e-03+9.83715259e-03j
7.93184137e-03+1.09172431e-02j 8.68098334e-03+1.22153302e-02j
9.59849587e-03+1.38104257e-02j 1.07543648e-02+1.58245673e-02j
1.22626616e-02+1.84567894e-02j 1.43228791e-02+2.20552997e-02j
1.73184855e-02+2.72895665e-02j 2.20928119e-02+3.56320579e-02j
3.09340251e-02+5.10781465e-02j 5.29887688e-02+8.95991148e-02j
2.06796515e-01+3.58182070e-01j -1.01530983e-01-1.80188467e-01j
-3.95959767e-02-7.20248143e-02j -2.41194538e-02-4.49825912e-02j
-1.70793655e-02-3.26698130e-02j -1.30517352e-02-2.56154726e-02j
-1.04419975e-02-2.10352675e-02j -8.61246205e-03-1.78157334e-02j
-7.25817638e-03-1.54244100e-02j -6.21493863e-03-1.35746033e-02j
-5.38648865e-03-1.20982516e-02j -4.71265827e-03-1.08903107e-02j
-4.15390282e-03-9.88174432e-03j -3.68316049e-03-9.02530927e-03j
-3.28128580e-03-8.28758191e-03j -2.93435135e-03-7.64424662e-03j
-2.63198294e-03-7.07718884e-03j -2.36629405e-03-6.57263458e-03j
-2.13118227e-03-6.11992184e-03j -1.92185176e-03-5.71066695e-03j
-1.73448150e-03-5.33818515e-03j -1.56598978e-03-4.99707947e-03j
-1.41386395e-03-4.68294334e-03j -1.27603520e-03-4.39214197e-03j
-1.15078510e-03-4.12164909e-03j -1.03667490e-03-3.86892339e-03j
-9.32491301e-04-3.63181383e-03j -8.37204509e-04-3.40848620e-03j
-7.49935327e-04-3.19736558e-03j -6.69929184e-04-2.99709088e-03j
-5.96535405e-04-2.80647843e-03j -5.29190567e-04-2.62449276e-03j
-4.67405004e-04-2.45022284e-03j -4.10751821e-04-2.28286264e-03j
-3.58857874e-04-2.12169516e-03j -3.11396340e-04-1.96607911e-03j
-2.68080544e-04-1.81543789e-03j -2.28658837e-04-1.66925022e-03j
-1.92910301e-04-1.52704227e-03j -1.60641160e-04-1.38838098e-03j
-1.31681760e-04-1.25286826e-03j -1.05884031e-04-1.12013605e-03j
-8.31193528e-05-9.89841973e-04j -6.32767636e-05-8.61665563e-04j
-4.62614628e-05-7.35304896e-04j -3.19935653e-05-6.10473593e-04j
-2.04070777e-05-4.86898124e-04j -1.14490704e-05-3.64315329e-04j
-5.07902537e-06-2.42470139e-04j -1.26834327e-06-1.21113433e-04j
-9.00020799e-16+0.00000000e+00j]

（上图即为图2）

（图3）

上面的复数列表是fft的运算结果

图2即为我们的傅里叶变换结果的图示，可以直观地看到我们将信号分为了四个频段，正好分别对应我们的信号函数y里面，每一个余弦函数的频率（单位Hz）。

四、参考资料

https://zhidao.baidu.com/question/553446922110370412.html
https://zhidao.baidu.com/question/553446922110370412.html
https://www.cnblogs.com/chester-cs/p/11630779.html
https://baike.baidu.com/item/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2

五、作者

欢迎大家一起学习交流，作者水平有限，若有错漏之处，敬请斧正！