laizhenghua

数据结构-图（Graph）案例代码Java/Python均有实现

数据结构-图（Graph）

图（Graph）也是一种数据结构，在计算机科学中除了线性表和树结构，还有一种图结构！这种结构节点可以具有零个或多个相邻的元素，非常适合表示多对多的关系！

1、为什么要有图？

我们已经学过了线性表和树结构，它们都有各自的应用场景。

然而线性表局限于一个直接前驱和一个直接后继的关系，也就是说集合中必存在唯一的一个"第一个元素"，必存在唯一的一个"最后元素"，除了最后一个元素之外，均有唯一的后继。除了第一个元素之外，均有唯一的前驱。

而树（Tree）的局限就是只能有一个直接的前驱（父节点），因此我们想要在计算机中表示多对多的关系时，就不得不使用图（Graph）这种数据结构来表示！

2、图的基本介绍

2.1、图的概述

图（Graph）是一种非线性的数据结构，是一些"顶点"的集合，这些顶点通过一系列"边"结对连接。其中节点可以具有零个或多个相邻的元素。两个节点之间的连接称为边。节点也可以称为顶点。如图

所有的顶点构成一个顶点集合，所有的边构成边集合，一个完整的图结构就是由顶点集合和边集合组成。另外图结构在交通运输网、地铁网络、社交网络等都可以抽象成图结构，从而进行存储与计算！

2.2、图的常用名词解释

1、顶点（Vertex）：顶点也称节点！顶点可以存储图结构的数据元素

2、边（Edge）：连接顶点的线，也可保存权值！例如某两点之间的距离

3、路径：比如3->4的路径有①3->1->4②3->2->1->4

4、无向图（Undirected Graph）：顶点之间的连接没有方向（如上图），比如1-2，既可以1->2也可以2->1。

5、有向图（Directed Graph）：顶点之间的连接或边具有方向性！描述两个顶的顺序就有要求，比如2-1，只能是2->1不能是1->2，如下图所示

6、带权图：边带有权值的图，如下图

2.3、图的表示方式

图在计算机中表示方式有两种：

二维数组表示（邻接矩阵）
链表表示（邻接表）

1、邻接矩阵

邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是通过row和col来表示1…n。

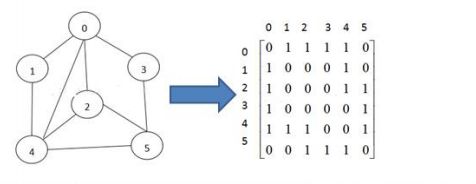
例如上图row={0, 1, 2, 3, 4, 5}，col={0, 1, 2, 3, 4, 5}。row和col共同组成一个二维数组！arry[row][col] = 0表示没有直连关系，arry[row][col] = 1表示有直连关系，例如array[0][1] = 1就表示0和1顶点是相连的。而如果值等于0说明不相连（不互通）。

2、邻接表

1、邻接矩阵（二维数组）需要为每个顶点都分配 n 个边的空间，其实有很多边都是不存在，会造成空间的一定损失
2、邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成
3、举例说明

2.4、图的创建入门代码

前面已经介绍了图结构的基本概念与表示方式，现在我们来快速使用代码创建一个图结构，体验图结构的表示方式。

要求代码实现（上图）图结构。备注：通过二维数组表示时规定 1 有直连关系，0 没有直连关系。

思路分析：

顶点元素通过一个集合存储
矩阵通过二维数组表示

Java代码实现：

package com.laizhenghua.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * @description: 图结构的创建
 * @date: 2021/11/20 13:34
 */
public class Graph {
    private List<String> vertexList; // 存储顶点
    private int[][] edges; // 存储邻接矩阵
    private int numberOfEdges; // 边的个数
    private boolean[] isVisited; // 记录某个顶点是否被访问过（后面遍历需要用到）

    // 构造器
    public Graph(int n) {
        this.vertexList = new ArrayList<>(n);
        this.edges = new int[n][n];
        this.numberOfEdges = 0;
        this.isVisited = new boolean[n];
    }
    // 插入节点
    public void insertVertex(String vertex) {
        this.vertexList.add(vertex);
    }

    /**
     * 添加边
     * @param v1 横向坐标（row的下标）
     * @param v2 纵向坐标（col的下标）
     * @param weight 权值
     */
    public void insertEdge(int v1, int v2, int weight) {
        this.edges[v1][v2] = weight;
        this.edges[v2][v1] = weight;
        this.numberOfEdges++;
    }
    // 获取顶点个数
    public int getNumberOfVertex() {
        return this.vertexList.size();
    }
    // 获取边的个数
    public int getNumberOfEdges() {
        return this.numberOfEdges;
    }
    // 通过索引从集合里面获取顶点
    public String getVertex(int index) {
        return this.vertexList.get(index);
    }
    // 获取v1和v2的权值
    public int getWeight(int v1, int v2) {
        return this.edges[v1][v2];
    }
    // 显示图对应的矩阵
    public void showGraph() {
        for (int[] array : this.edges) {
            System.out.println(Arrays.toString(array));
        }
    }
}

main方法中测试

/**
 * @description:
 * @date: 2021/11/20 13:33
 */
public class GraphTest {
    public static void main(String[] args) {
        int n = 5; // 顶点个数
        String[] vertexArray = new String[]{"A", "B", "C", "D", "E"};
        // 创建图对象
        Graph graph = new Graph(n);
        // 循环添加顶点
        for (String vertex : vertexArray) {
            graph.insertVertex(vertex);
        }
        // 添加边。A-B A-C B-C B-D B-E
        graph.insertEdge(0, 1, 1); // A-B
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        // 输出矩阵
        graph.showGraph();
    }
}

输出矩阵如下：

Python代码实现：

# !usr/bin/env python
# -*- coding:utf-8 -*-
# __author__ = "laizhenghua"

import numpy as np

class Graph:
    def __init__(self, n):
        self.vertex_list = []
        self.edges = np.zeros((n, n), dtype=int)  # 5 * 5 的矩阵
        self.number_of_edges = 0
        self.is_visited = []  # 存放布尔值记录某个顶点是否被访问过（后面遍历需要用到）

    # 添加顶点
    def inset_vertex(self, vertex):
        self.vertex_list.append(vertex)
        
    # 添加边
    def insert_edge(self, v1, v2, weight):
        self.edges[v1][v2] = weight
        self.edges[v2][v1] = weight
        self.number_of_edges += 1
        
    # 获取顶点个数
    def get_number_of_vertex(self):
        return len(self.vertex_list)
        
    # 获取边个数
    def get_number_of_edges(self):
        return self.number_of_edges
        
    # 通过索引获取列表里面的顶点
    def get_vertex_by_index(self, index):
        return self.vertex_list[index]
        
    # 获取v1和v2对应的权值
    def get_weight(self, v1, v2):
        return self.edges[v1][v2]
        
    # 显示图对应的矩阵
    def show_graph(self):
        for i in range(len(self.edges)):
            for j in range(len(self.edges[i])):
                print(self.edges[i][j], end=" ")
            print()

if __name__ == "__main__":
    n = 5  # 顶点个数
    graph = Graph(n)  # 创建图对象
    vertex_list = ["A", "B", "C", "D", "E"]

    # 循环添加顶点
    for vertex in vertex_list:
        graph.inset_vertex(vertex)
    # 添加边
    graph.insert_edge(0, 1, 1)
    graph.insert_edge(0, 2, 1)
    graph.insert_edge(1, 2, 1)
    graph.insert_edge(1, 3, 1)
    graph.insert_edge(1, 4, 1)
	
	# 输出邻接矩阵
    graph.show_graph()

3、图的遍历

所谓图的遍历，即是对图顶点的访问！一个图有那么多个顶点，如何遍历这些顶点，需要特定策略（如二叉树的遍历有前序、中序、后序）。

而对于图的遍历一般由两种访问策略：

深度优先遍历（Depth First Search），简称DFS
广度优先遍历（Broad First Search），简称BFS

3.1、深度优先遍历

深度优先，从字面上理解就是图的深度优先查找！其遍历的基本思想如下：

深度优先遍历，从初始访问结点出发，初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点，可以这样理解：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
我们可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。
显然，深度优先搜索是一个递归的过程

根据遍历的基本思想，我们得出深度优先遍历的算法步骤（假设初始节点为v）：

访问初始结点 v，并标记结点 v 为已访问。
查找结点 v 的第一个邻接结点 w。
若 w 存在，则继续执行 4，如果 w 不存在，则回到第 1 步，将从 v 的下一个结点继续。
若 w 未被访问，对 w 进行深度优先遍历递归（即把 w 当做另一个 v，然后进行步骤 123）。
查找结点 v 的 w 邻接结点的下一个邻接结点，转到步骤 3。

案例（我们还是以刚才创建的图结构进行深度优先遍历）：

深度优先算法Java代码实现（Graph类新增方法）：

// 获取第一个邻接节点的下标
public int getFirstNeighbor(int index) {
    for (int i = 0; i < this.vertexList.size(); i++) {
        if (this.edges[index][i] > 0) {
            return i;
        }
    }
    return -1; // 如果不存在则返回-1
}
// 根据前一个邻接节点的下标来获取下一个邻接节点
public int getNextNeighbor(int v1, int v2) {
    for (int i = v2 + 1; i < this.vertexList.size(); i++) {
        if (this.edges[v1][i] > 0) {
            return i;
        }
    }
    return -1;
}

/**
 * 深度优先遍历算法
 * @param isVisited 记录节点被访问过的boolean数组
 * @param index 第一次就是0
 */
private void dfs(boolean[] isVisited, int index) {
    // 首先我们访问该节点（输出）
    System.out.print(getVertexByIndex(index) + "->");
    // 将节点标记为已经访问过
    isVisited[index] = true;
    // 查找节点下标为index的第一个邻接节点w
    int w = getFirstNeighbor(index);
    while (w != -1) {
        if (!isVisited[w]) {
            dfs(isVisited, w);
        }
        // 如果w节点已经被访问过了
        w = getNextNeighbor(index, w);
    }
}
// 对dfs进行一个重载，遍历所有的节点，并进行dfs
public void dfs() {
    // 遍历所有节点，进行dfs[类似回溯]
    for (int i = 0; i < getNumberOfVertex(); i++) {
        if (!isVisited[i]) {
            dfs(isVisited, i);
        }
    }
    isVisited = new boolean[getNumberOfVertex()];
}

在main方法中测试

// 图的深度优先遍历
graph.dfs(); // A->B->C->D->E->

深度优先算法Python代码实现（Graph类新增方法）：

# 获取第一个邻接节点的下标
def get_first_neighbor(self, index):
    for i in range(len(self.vertex_list)):
        if self.edges[index][i] > 0:
            return i
    return -1

# 根据前一个邻接节点的下标来获取下一个邻接节点
def get_next_neighbor(self, v1, v2):
    for i in range(v2 + 1, len(self.vertex_list), 1):
        if self.edges[v1][i] > 0:
            return i
    return -1

# 深度优先遍历算法
def dfs(self, *args):
    if len(args) == 0:
        for i in range(self.get_number_of_vertex()):
            if self.is_visited[i] is not True:
                self.dfs(self.is_visited, i)
        self.is_visited = [False] * len(self.vertex_list)
    if len(args) == 2:
        # 首先我们访问该节点（输出）
        print(self.get_vertex_by_index(args[1]) + "->", end="")
        # 将节点标记为已经访问过
        args[0][args[1]] = True
        w = self.get_first_neighbor(args[1])
        while w != -1:
            if self.is_visited[w] is not True:
                self.dfs(args[0], w)
            w = self.get_next_neighbor(args[1], w)

3.2、广度优先遍历

图的广度优先搜索/遍历（Broad First Search）：类似于一个分层搜索的，广度优先遍历需要使用一个队列以保持访问过的节点顺序，以便按这个顺序来访问这些节点的邻接节点。

其算法步骤如下：

访问初始结点 v 并标记结点 v 为已访问。
结点 v 入队列
当队列非空时，继续执行，否则算法结束。
出队列，取得队头结点 u。
查找结点 u 的第一个邻接结点 w。
若结点 u 的邻接结点 w 不存在，则转到步骤 3，否则循环执行以下三个步骤：
1. 若结点 w 尚未被访问，则访问结点 w 并标记为已访问。
2. 结点 w 入队列
3. 查找结点 u 的继 w 邻接结点后的下一个邻接结点 w，转到步骤 6。

深度优先算法Java代码实现（Graph类新增方法）：

// 对一个节点进行广度优先遍历
private void bfs(boolean[] isVisited, int index) {
    int u; // 队列头节点对应的下标
    int w; // 邻接节点w
    LinkedList<Integer> queue = new LinkedList<>(); // 队列，记录节点访问顺序
    // 访问节点/输出节点信息
    System.out.print(getVertexByIndex(index) + "->");
    // 将节点标记为已访问
    isVisited[index] = true;
    // 将节点加入队列
    queue.addLast(index);
    while (!queue.isEmpty()) {
        u = queue.removeFirst(); // 取出队列头结点下标
        w = getFirstNeighbor(u); // 获取第一个邻节点的下标
        if (w != -1) {
            if (!isVisited[w]) {
                System.out.print(getVertexByIndex(w) + "->");
                isVisited[w] = true; // 将节点标记为已访问
                queue.addLast(w); // 入队
            }
            // 以u为前驱点，找w后面的下一个邻节点
            w = getNextNeighbor(u, w); // 体现出广度优先
        }
    }
}

// 对所有节点进行广度优先遍历
public void bfs() {
    for (int i = 0; i < getNumberOfVertex(); i++) {
        if (!isVisited[i]) {
            bfs(isVisited, i);
        }
    }
    isVisited = new boolean[getNumberOfVertex()];
}