八大排序详解 (图文 + c++代码)
文章目录
-
-
- 基本性质:
- 一.插入排序
-
- 1.直接插入
- 2.折半插入
- 3.希尔排序
- 二.交换排序
-
- 1.冒泡排序
- 2.快速排序
- 三.选择排序
-
- 1.简单选择排序
- 2.堆排序
- 四.归并排序
- 五.基数排序
- 内部排序算法比较:
-
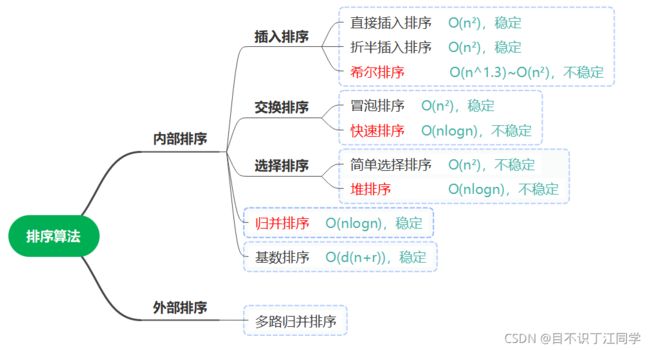
基本性质:
稳定性:未排序的 R i , R j R_i,R_j Ri,Rj的关键字相等 k e y i = k e y j key_i=key_j keyi=keyj,若排序之后 R i , R j R_i,R_j Ri,Rj相对位置不变,则该排序算法是稳定的,否则是不稳定的。
内部排序:排序期间元素全部在内存中。
外部排序:排序期间元素无法全部同时放入内存,需要不断地在内、外存之间切换。
一.插入排序
插入排序分为排序序列、待排序列。每次将待排序列的一个元素插入到已排好序列里面。
1.直接插入
\qquad 即将序列分成有序、无序的两部分,初始时有序部分为最左边1个,无序部分为右边的n-1个。
\qquad 通过n-1趟排序,每一趟将右边无序部分的第一个元素插入到左边有序部分中(边比较边移动),最终获得排序序列。
![]()
//1.插入排序
void insertsort(int a[],int n) { //直接插入,O(n^2),稳定
int i, j;
for (i = 2; i <= n; i++){
if (a[i - 1] > a[i]) {
a[0] = a[i]; //哨兵
for (j = i - 1; a[j] > a[0]; j--) //判断条件为a[j] > a[0]
a[j + 1] = a[j]; //比a[i](哨兵)大的后移
a[j + 1] = a[0]; //哨兵归位
}
}
}
\qquad 每一趟,我们需要将a[j]与他前面的元素比较。在此我们将a[0]=a[j],设a[0]为哨兵,减少了越界的判断。
\qquad 每次只需要比较a[j-1]与a[0]的大小,a[j-1]>a[0],就将a[j-1]复制后移即可。最后将a[0]回归到正确位置。
小技巧:
- 通过哨兵,减少了对是否越界的判断(因为到a[0]就会停止)
- 通过赋值,来交换元素的值(快排亦有应用)
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | 稳定 | O ( 1 ) O(1) O(1) | 顺序表、线性表 |
适合于基本有序的排序表和数据量不大的排序表。
2.折半插入
每趟插入我们需要做两件事:
\qquad 1.找到元素插入的位置
\qquad 2.给插入的元素挪空间
\quad 前面的直接插入,我们是每次边比较边移动,而折半插入将比较和移动分开,先用二分查找找到插入位置,再将元素整体后移,再插入。
void halfinsert(int a[], int n) { //折半插入,O(n^2),稳定
int i, j, low, high, mid;
for (i = 2; i <= n; i++) {
a[0] = a[i];
low = 1, high = i - 1;
while (low <= high) { //<=,因为在等于时也要处理
mid = (low + high) / 2;
if (a[mid] > a[0]) high = mid - 1; //保证high后面的都大于a[i]
else low = mid + 1;
}
for (j = i - 1; j >= high+1; j--) //将high后面的集体后移
a[j + 1] = a[j];
a[high + 1] = a[0]; //哨兵归位
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | 稳定 | O ( 1 ) O(1) O(1) | 顺序表 |
相比于直接插入减少了比较次数,移动次数不变。复杂度稳定性也不变。
3.希尔排序
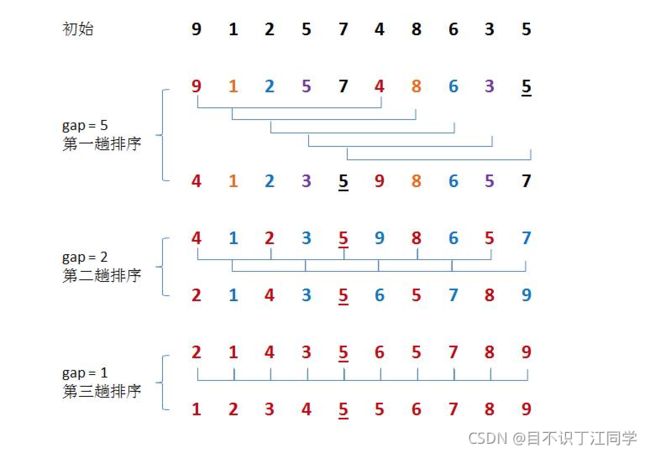
shell排序又称缩小增量排序。
\qquad 具体步骤:先取步长 d 1 d_1 d1,我们将排序表分为 d 1 d_1 d1 个 L [ i , i + d 1 , i + 2 d 1 , . . . , i + k d 1 ] L[i,i+d_1,i+2d_1,...,i+kd_1] L[i,i+d1,i+2d1,...,i+kd1] 的子表 ( i = 0 , 1 , . . , d − 1 ) (i=0,1,..,d-1) (i=0,1,..,d−1),即把相邻 d 1 d_1 d1 的元素组成一个子表。对每个子表进行直接插入排序,然后继续选择 d 2 < d 1 d_2
一般取 d 1 = n / 2 , d i + 1 = ⌊ d i / 2 ⌋ , d 最 后 = 1 d_1=n/2,d_{i+1}=\lfloor d_i/2\rfloor,d_{最后}=1 d1=n/2,di+1=⌊di/2⌋,d最后=1
void shellsort(int a[], int n) { //希尔排序,最坏O(n^2),最好O(n^1.3),不稳定
int dk, i, j; //对大量数据极其有效!
for (dk = n / 2; dk >= 1; dk = dk / 2) //不同步长dk
for (i = dk + 1; i <= n; i++)
if (a[i] < a[i - dk]) {
a[0] = a[i];
for (j = i - dk; j > 0 && a[0] < a[j]; j = j - dk) //处理移动时,前一个是i-dk,每次j=j-dk
a[j + dk] = a[j]; //后一个为j+dk
a[j + dk] = a[0]; //哨兵归位
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | 不稳定 | O ( 1 ) O(1) O(1) | 顺序表 |
具体时间负责度由增量序列决定,n为某个范围时可取到 n 1.3 n^{1.3} n1.3,最坏时为 O ( n 2 ) O(n^2) O(n2)
二.交换排序
交换排序即通过比较关键字的大小来交互这两个元素的位置。
1.冒泡排序
\qquad 进行n趟,每一趟从后向前两两比较相邻元素的值,若逆序(a[i-1]>a[i])即交换。
\qquad 每一趟均可将序列中的最小值,放到序列的最终位置上,若没有交换(flag==0),即已经有序。
void bubblesort(int a[], int n) { //冒泡排序,O(n^2),稳定
bool flag; //对大量数据极其低效!
int i, j;
for (i = 0; i < n-1; i++) { //计数n趟
flag = 0; //判断是否有交换
for (j = n-1; j > i; j--) //从尾向头遍历
if (a[j - 1] > a[j]) { //逆序即交换
swap(a[j], a[j - 1]);
flag = 1;
}
if (flag == 0) //无交换停止
return;
}
}
![]()
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | 稳定 | O ( 1 ) O(1) O(1) | 顺序表 |
因为添加了flag判断是否有交换,无交换结束,所有顺序时为O(n)。
2.快速排序
\qquad 快速排序是利用分治法的思想,每次选择一个枢轴元素pivot(一般取首元素),通过一趟排序将待排序表 L[1…n] 分成两个独立的部分:L[1…k-1] 、 L[k+1…n] 。
\qquad 使得 L[1…k-1] 中所有元素均 ≤ \le ≤ pivot,L[k+1…n] 中所有元素都 ≥ \ge ≥pivot,pivot处在其最终位置 L[k] 上。然后继续对左右两部分递归进行。
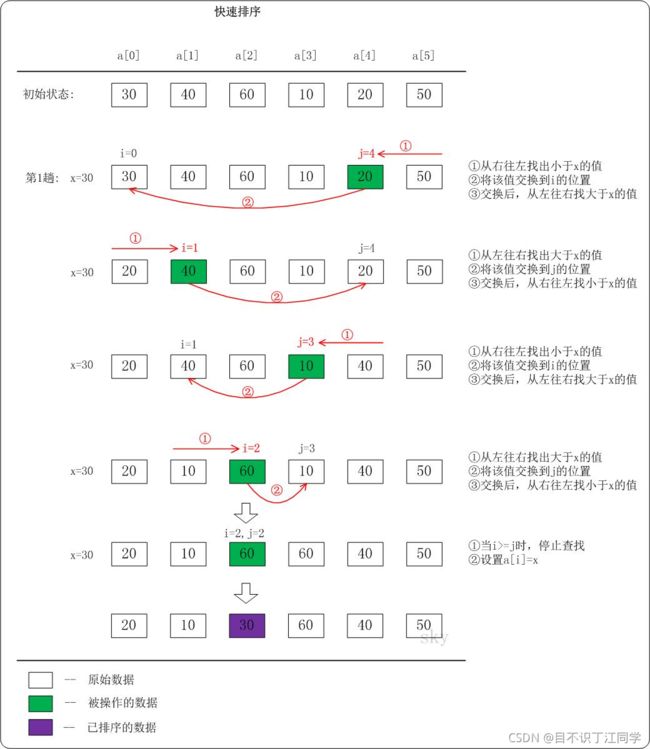
\qquad 划分操作 partition:每次划分操作将pivot放到最终位置,且将原序列划分为 ≤ \le ≤pivot 和 ≥ \ge ≥pivot 到两个子序列。快排是交换排序是因为在划分子序列的过程中,我们需要交换两个子序列的值。为了减小时间复杂度,快排不是直接3次赋值交换,而是通过一次左右赋值实现,每次交换只需要一次赋值,大大降低了复杂度,最后 low==high 时停止,最后把pivot赋值给 a[low] 或者 a[high] 。
\qquad 赋值操作:从右开始,high指针左移到第一个小于pivot的元素,将其赋给a[low](取第一个元素为pivot)。此时a[high]不变,接着low指针右移到第一个大于pivot到元素,将其赋给a[high]。此时a[low]不变。
\qquad 就这样不断左右赋值,使得low左边全都小于pivot,high右边全都大于pivot。当low==high时结束,最后我们将pivot放到low/high到位置即可。
//快排:每次确定枢纽元素的正确位置。划分过程:先右后左,一次交替赋值达到交互目的,降低复杂度
int partition(int a[], int low, int high) { //一趟划分,确定基准元素+交互两边使得有序
int pivot = a[low];
while (low < high) { //最终 low==high 停止,停在最后一个被赋值移动的元素上
while (low < high && a[high] >= pivot) high--; //从右找到第一个
a[low] = a[high];
while (low < high && a[low] <= pivot) low++; //从左找到第一个 >pivot的:a[low]
a[high] = a[low];
}
a[low] = pivot; //哨兵t归位(此时high=low,任选一个即可)
return low;
}
void quicksort(int a[], int low,int high) { //O(nlogn),不稳定,平均最优,最差O(n^2)
if (low < high) {
int pivot = partition(a, low, high);
quicksort(a, low, pivot - 1);
quicksort(a, pivot + 1, high);
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( n l o g n ) O(nlogn) O(nlogn) | 不稳定 | O ( l o g n ) − O ( n ) O(logn)-O(n) O(logn)−O(n) | 顺序表 |
快排是所有内部排序算法中平均性能最优的排序算法!!!
快排是递归操作需要递归工作栈,最坏是待排序列有序序列,需要 O ( n ) O(n) O(n)空间 O ( n 2 ) O(n^2) O(n2)的时间,最好是每次对半划分,需要 O ( l o g n ) O(logn) O(logn)空间 O ( n l o g n ) O(nlogn) O(nlogn)时间,平均需要 O ( l o g n ) O(logn) O(logn)空间 O ( n l o g n ) O(nlogn) O(nlogn)时间。
快排每趟均会把枢轴元素(pivot)放到最终的位置上。
三.选择排序
选择排序:每一趟选择出待排序列中关键字最小的元素。
1.简单选择排序
每次选出最小的元素,比较次数与序列初始状态无关,总是 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)次
void selectsort(int a[], int n) { //简单选择,O(n^2),不稳定
int minp, j;
for (int i = 0; i < n-1; i++) {
minp = i; //只需要最小值的索引即可
for (j = i + 1; j < n; j++)
if (a[j] < a[minp])
minp = j;
if (minp != j)
swap(a[i], a[minp]);
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( 1 ) O(1) O(1) | 顺序表 |
2.堆排序
堆即顺序存储的完全二叉树。一维数组 ⟶ \longrightarrow ⟶ 看作是完全二叉树
大根堆:孩子结点均小于父结点的堆。
小根堆:孩子结点均大于父结点的堆。
堆排序过程:
\qquad 1.构造初始堆
\qquad 2.排序:不断将堆顶与堆末端交换 ,然后调整剩下的堆
调整:对以 i i i 为根的子树进行调整,将根 i 其与左右子间最大子进行比较,若大于则无需调整。若小于,则将根与较大的结点交换位置,对交换位置的根继续进行向下筛选。
1.建堆:现有一个n个结点的完全二叉树最后一个叶子为 n ,其父结点为 ⌊ n 2 ⌋ \lfloor \frac{n}{2} \rfloor ⌊2n⌋,我们对以 ⌊ n 2 ⌋ \lfloor \frac{n}{2} \rfloor ⌊2n⌋为根结点的子树进行筛选,是该子树成为堆。
我们依次对以 ⌊ n 2 ⌋ → 1 \lfloor \frac{n}{2} \rfloor\to 1 ⌊2n⌋→1 为根的子树进行筛选,子树每一层都进行调整,使得每个子树都为根。
输出堆顶:输出堆顶元素后,将堆的最后一个元素与堆顶元素交换。对根进行筛选,调整回堆。
2.排序:对于建好的堆(1~n),每次将根(最大值)和堆的末端交换swap(a[1],a[n]),然后调整堆(1~n-1)。接着对堆(1~n-1)进行同样的操作,直至堆只剩下1个元素
//调整
void heapadjust(int a[], int k, int len) { //对以i为根的子树进行调整
a[0] = a[k];
for (int i = 2 * k; i <= len; i = 2 * i) { //每次向下一层
if (i < len&& a[i] < a[i + 1])
i++; //i为较大子
if (a[0] >= a[i]) //满足堆性质,不需要调整
break;
else {
a[k] = a[i]; //将左右子较大者与根交换
k = i; //同时将根调整到被交换的位置上
}
}
a[k] = a[0];
}
//建大根堆
void bulidmaxheap(int a[],int len){
for(int i=len/2;i>=1;i--) //对根 n/2~1 均调整一遍
heapadjust(a,i,len);
}
//堆排序
void heapsort(int a[],int len){
build a heap(a,len);
for(int i=len;i>1;i—-){
swap(a[i],a[1]); //每次将最大值根交换到后面去
heapadjust(a,1,i-1);//对剩下的同样操作
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o n g ) O(nlong) O(nlong) | O ( n l o g n ) O(nlogn) O(nlogn) | 不稳定 | O ( 1 ) O(1) O(1) | 顺序表 |
建堆时间 O ( n ) O(n) O(n),排序过程需要 n − 1 n-1 n−1 次调整,每次调整 O ( l o g n ) O(logn) O(logn)。堆排序最坏、最好、平均情况均是 O ( n l o g n ) O(nlogn) O(nlogn),与归并排序相同。
适合关键字较多的情况,比如从1亿个数中选出前100个最大的值?
使用大小为100的数组,建立小根堆,依次读入所有值,若小于堆顶则舍弃,若大于堆顶则取代堆顶并重新调整堆。读完数据,堆中100个数即为所求。
元素间比较次数:每次都是左右子间一次比较,较大者与父结点一次比较。若只有一个孩子,则没有左右点间比较,只有父子间一次比较。
四.归并排序
归并:将两个或以上的有序表合并成一个新的有序表。
归并排序也是基于分治法思想,对于n个元素的归并排序,先将n个元素划分成 n 个长为 1 的有序子表,再将这些子表两两归并,得到 ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈2n⌉ 个长为2 或 1的有序子表,继续两两归并….
一趟归并:对所有子表进行一次两两归并。
n个元素共 ⌈ l o g n ⌉ \lceil logn \rceil ⌈logn⌉趟。
归并操作:将前后相邻的两个有序表合并成一个新的有序表,需要一个辅助数组B[n]。
int b[N+1]; //辅助数组
void merge(int a[],int low,int mid,int high){
for(int k=low;k<=high;k++)
b[k]=a[k]; //把a所有元素复制到b中
int i,j;
for(i=low,j=mid+1,k=low;i<=mid&&j<=high;){
if(b[i]<=b[j])
a[k++]=b[i++];
else
a[k++]=b[j++]
}
while(i<=mid) a[k++]=b[i++]; //将剩余部分放后面去
while(j<=high) a[k++]=b[j++];
}
void mergesort(int a[],int low,int high){
if(low<high){
int mid=(low+high)/2;
mergesort(a,low,mid);
mergesort(a,mid+1,high); //递归
merge(a,mid,high); //合并
}
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o n g ) O(nlong) O(nlong) | O ( n l o g n ) O(nlogn) O(nlogn) | 稳定 | O ( n ) O(n) O(n) | 顺序表 |
n个元素的归并排序,刚好需要n个空间,空间复杂度是 O ( n ) O(n) O(n)
每趟是O(n),共 ⌈ l o g n ⌉ \lceil logn \rceil ⌈logn⌉ 趟,故时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)
五.基数排序
\qquad 与前面所有排序方法不一样,基数排序不基于比较和移动,而是基于关键字各位的大小进行排序,所以可以进行基数排序的元素必须具有基数radix——基数即基本单元数,即进制(radix),十进制基数为10(基本单元为0123456789)。
如果是十进制数,可以根据个位、十位、百位…等位进行排序,同样也可对浮点数排序。
1.最高位优先(MSD):
\qquad 从高位到低位,逐层划分成若干子序列,依次进行排序,然后将所有子序列依次连接成一个有序序列。
2.最低位优先(LSD):(重要)
\qquad 按由低到高的顺序排序,每次都是对整个序列整体操作,不产生子序列。
以最低位优先基数排序为例,对于 n n n 个结点 a 0 , a 1 , . . . , a n − 1 a_0,a_1,...,a_{n-1} a0,a1,...,an−1,每个结点值为 d d d 位 r r r 进制整数,就要做 d 次“分配”和“收集”。
分配:将 q [ 0 ] , q [ 1 ] , . . . , q [ r − 1 ] q[0],q[1],...,q[r-1] q[0],q[1],...,q[r−1]各个队列置成空队,依次考查每个结点 a i a_i ai, ( i = 0 , 1 , . . . , n − 1 ) (i=0,1,...,n-1) (i=0,1,...,n−1),第 j j j 位为 k k k,就放入 q [ k ] q[k] q[k]队列中。
收集:将 q [ 0 ] , . . . , q [ r − 1 ] q[0],...,q[r-1] q[0],...,q[r−1]各个队列中的结点首尾相接,得到新的结点序列,从而得到新的链表。
int maxbit(int a[], int n) { //求数据的最大位数d O(n)
int maxData = a[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
if (maxData < a[i])
maxData = a[i];
int d = 1;
while (maxData >= 10){
maxData /= 10;
++d;
}
return d;
}
void radixsort(int a[], int n) { //基数排序,r=10(10进制)
int d = maxbit(a, n); //最大位数 d ,d次分配+收集
int* tmp = new int[n];
int* count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for (i = 1; i <= d; i++) { //进行d次排序
for (j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for (j = 0; j < n; j++){
k = (a[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for (j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for (j = n - 1; j >= 0; j--){ //将所有桶中记录依次收集到tmp中
k = (a[j] / radix) % 10;
tmp[count[k] - 1] = a[j];
count[k]--;
}
for (j = 0; j < n; j++) //将临时数组的内容复制到data中
a[j] = tmp[j];
radix = radix * 10;
}
delete[]tmp;
delete[]count;
}
| 平均 | 最坏 | 最好 | 稳定性 | 空间 | 适用 |
|---|---|---|---|---|---|
| O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | 稳定 | O ( r ) O(r) O(r) | 顺序表 |
n个 r进制(radix进制),d位数(digit位数),进行排序 ⟶ \longrightarrow ⟶ n个元素,r个队列,d次分配收集
要进行 d 趟分配+收集,一趟分配:O(n),一趟收集:O(r)
位数 d 越少,复杂度越小。10进制下, O ( d ( n + 10 ) ) O(d(n+10)) O(d(n+10)),可以只看 O ( d n ) O(dn) O(dn)
小于15位时,基数排序明显快于一众O(nlogn)的排序(快排,归并,堆排),当 d = 15 d=15 d=15 时, O ( 15 n ) ≈ O ( n l o g n ) O(15n)\approx O(nlogn) O(15n)≈O(nlogn) 。
int型整数的范围为 − 2 32 ∼ 2 32 − 1 -2^{32}\sim 2^{32}-1 −232∼232−1即 -2147483648~2147483647,共10位,int型整数的排序基本上基数排序/桶排序 快于O(nlogn)
比较排序的极限是 O ( n l o g n ) O(nlogn) O(nlogn),分配排序是O(n)).
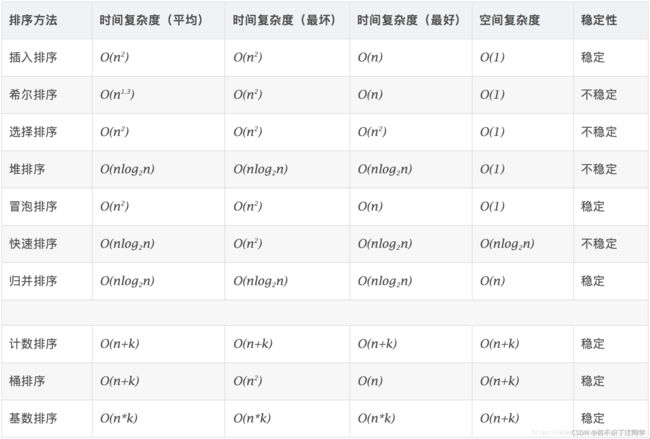
内部排序算法比较:
| 排序方法 | 平均 | 最坏 | 最好 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 不稳定 | |
| 简单选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 堆排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O(1) | 不稳定 |
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O(1) | 稳定 |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( n l o g n ) O(nlogn) O(nlogn) | O(logn) | 不稳定 |
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O(n) | 稳定 |
| 基数排序 | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)) | O(r) | 稳定 |