数字信号处理实验（二） —— 利用FFT实现快速卷积

前言

由第一个实验，我们大致知道了，可以通过卷积脉冲响应的方式，得到输出，得到经过一个系统处理过后的输出。如果这个系统是数字滤波器，那么输出就是滤波后的结果

所以 这一节介绍的FFT实现快速卷积意义不小，这意味着DSP的很多应用，比如快速滤波，快速陷波，都是可以实现的。

实践

数字滤波器脉冲响应为$h(n)=(\frac{1}{2}{)}^n{R}_{N_2}(n)$，$N_1=16,N_2=17$，输入序列有如下几种情况，我们要设计matlab程序得到滤波后的结果（就是和滤波器脉冲响应卷积后的结果）

• $$x(n)=R_{N_1}(n)$$
• $$x(n)=cos(\frac{2\pi }{N_1}n)R_{N_1}(n)$$
• $$x(n)=(\frac{1}{3}{)}^n{R}_{N_1}(n)$$

第一题

$$x(n)=R_{N_1}(n),N1=16$$

n=[0:1:16];
m=[0:1:17];
N1=length(n);
N2=length(m);

%输入Xn Hn
Xn=ones(1,N1);
Hn=0.5.^m.*ones(1,N2);

%修剪序列长度
N=N1+N2-1;
XK=fft(Xn,N);
HK=fft(Hn,N);
YK=XK.*HK;
Yn=ifft(YK,N);

if all(imag(Xn)==0)&(all(imag(Hn)==0))
    Yn=real(Yn);
end

%修剪横坐标序列长度
y=0:N-1;
h=0:N2-1;
x=0:N1-1;

subplot(1,4,1);
stem(x,Xn,'r*');
title({ '$$ Xn = R_{N1}(n) $$' },'Interpreter','latex');
axis([0,length(x),0,1.1]);

subplot(1,4,2);
stem(h,Hn,'r*');
title({ '$$ Hn $$' },'Interpreter','latex');
axis([0,length(h),0,1.1]);

subplot(1,4,3);
stem(y,Yn,'r*');
title({ '$$ Yn $$' },'Interpreter','latex');
axis([0,length(y),0,2.1]);

subplot(1,4,4);
Yline=conv(Xn,Hn);
stem(y,Yline,'r*');
title({ '$$ Xn*Hn $$' },'Interpreter','latex');
axis([0,length(y),0,2.1]);

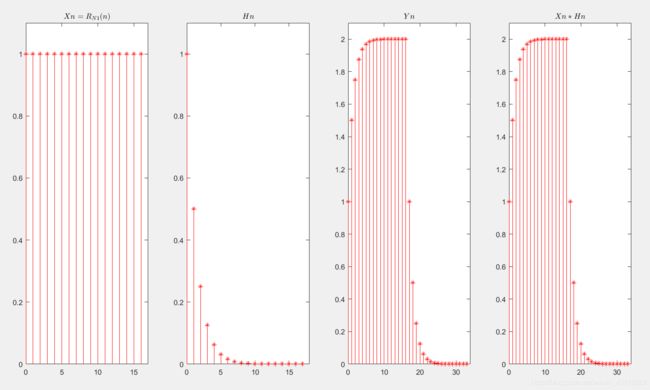
第一第二个分别就是源信号以及脉冲响应，后两个的对比，我们可以发现利用FFT进行的卷积和之前直接卷积的效果几乎相同

第二题

% 修改序列长度 N1=16 N2=17
n=[0:1:16];
m=[0:1:17];
N1=length(n);
N2=length(m);
% Xn Hn表达
Xn=cos(2*pi*n/N1);
Hn=0.5.^m.*ones(1,N2);
%修剪序列长度
N=N1+N2-1;

XK=fft(Xn,N);
HK=fft(Hn,N);
YK=XK.*HK;
Yn=ifft(YK,N);

%实序列的循环卷积 = 实序列
if all(imag(Xn)==0)&(all(imag(Hn)==0))
    Yn=real(Yn);
end

%修剪横坐标序列长度
y=0:N-1;
h=0:N2-1;
x=0:N1-1;
subplot(1,4,1);
stem(x,Xn,'r*');
title({ '$$ Xn = cos(\frac{2\pi}{N1}n) R_{N1}(n) $$' },'Interpreter','latex');
axis([0,length(x),-1.1,1.1]);

subplot(1,4,2);
stem(h,Hn,'r*');
title({ '$$ Hn $$' },'Interpreter','latex');
axis([0,length(y),0,1.1]);

subplot(1,4,3);
stem(y,Yn,'r*');
title({ '$$ Yn $$' },'Interpreter','latex');
axis([0,length(h),-2.1,2.1]);

subplot(1,4,4);
Yline=conv(Xn,Hn);
stem(y,Yline,'r*');
title({ '$$ Xn*Hn $$' },'Interpreter','latex');
axis([0,length(h),-2.1,2.1]);

第三题

clear all;
n=[0:1:16];
m=[0:1:17];

N1=length(n);
N2=length(m);

%生成Xn Hn
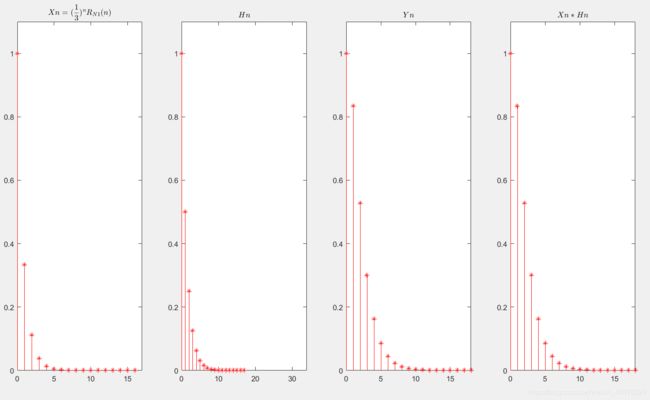
Xn=(1/3).^n;
Hn=0.5.^m.*ones(1,N2);
%修剪序列长度
N=N1+N2-1;
XK=fft(Xn,N);
HK=fft(Hn,N);
YK=XK.*HK;
Yn=ifft(YK,N);
%实序列的循环卷积 = 实序列
if all(imag(Xn)==0)&(all(imag(Hn)==0))
    Yn=real(Yn);
end

y=0:N-1;
h=0:N2-1;
x=0:N1-1;
subplot(1,4,1);
stem(x,Xn,'r*');
title({ '$$ Xn = (\frac{1}{3})^n R_{N1}(n) $$' },'Interpreter','latex');
axis([0,length(x),0,1.1]);

subplot(1,4,2);
stem(h,Hn,'r*');
title({ '$$ Hn $$' },'Interpreter','latex');
axis([0,length(y),0,1.1]);

subplot(1,4,3);
stem(y,Yn,'r*');
title({ '$$ Yn $$' },'Interpreter','latex');
axis([0,length(h),0,1.1]);

subplot(1,4,4);
Yline=conv(Xn,Hn);
stem(y,Yline,'r*');
title({ '$$ Xn*Hn $$' },'Interpreter','latex');
axis([0,length(h),0,1.1]);