数据结构与算法【B树】的Java实现+图解
目录
B树
特性
实现
节点准备
大体框架
实现分裂
实现新增
实现删除
完整代码
B树
也是一种自平衡的树形数据结构,主要用于管理磁盘上的数据管理(减少磁盘IO次数)。而之前说的AVL树与红黑树适合用于内存数据管理。存储一个100w的数据使用AVL存储,树高大约为20层(![]() ),如果使用磁盘IO查询20次效率较低。
),如果使用磁盘IO查询20次效率较低。
特性
度degree:指树中节点孩子数
阶order:指所有节点孩子数中最大值
一棵 B-树具有以下性质
特性1:每个节点 x 具有
- 属性 n,表示节点 x 中 key 的个数
- 属性 leaf,表示节点是否是叶子节点
- 节点 key 可以有多个,以升序存储
特性2:每个节点最多具有m个孩子,其中m叫做B-树的阶
特性3:除根结点与叶子节点外,每个节点至少有ceil(m/2)个孩子,根节点不是叶子节点时,最少有两个孩子。叶子节点没有孩子
特性2:每个非叶子节点中的孩子数是 n + 1。而n的取值为ceil(m/2)-1<=n<=m-1。
特性3:最小度数t(节点的孩子数称为度)和节点中键数量的关系如下:
| 最小度数t | 键数量范围 |
|---|---|
| 2 | 1 ~ 3 |
| 3 | 2 ~ 5 |
| 4 | 3 ~ 7 |
| ... | ... |
| n | (n-1) ~ (2n-1) |
其中,当节点中键数量达到其最大值时,即 3、5、7 ... 2n-1,需要分裂
特性4:叶子节点的深度都相同
实现
节点准备
B树的节点属性,与其他树不太相同,首先是key可以有多个,因此要设置为数组,孩子节点也未知,因此也要设置为数组。本应该还存在一个value属性,这里简化掉,不添加该属性。
static class Node {
boolean leaf = true; //是否是叶子节点
int keyNumber; //有效key
int t; //最小度
int[] keys; // keys数组
Node[] children; //孩子节点数组
public Node(int t) {
this.t = t;
this.keys = new int[2 * t - 1];
this.children = new Node[2 * t];//最大孩子节点个数为为2*t
}
@Override
public String toString() {
return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));
}
/**
* 根据key获取对应节点
*
* @param key
* @return
*/
Node get(int key) {
int i = 0;
while (i < keyNumber) {
//如果在该节点找到,那么直接返回即可
if (keys[i] == key) {
return this;
}
//说明要找的元素可能在children[i]中
if (keys[i] > key) {
break;
}
i++;
}
//如果是叶子节点,直接返回null
if (leaf) {
return null;
}
return children[i].get(key);
}
/**
* 指定位置插入元素
*
* @param key
* @param index
*/
void insertKey(int key, int index) {
System.arraycopy(keys, index, keys, index + 1, keyNumber - index);
keys[index] = key;
keyNumber++;
}
/**
* 向节点中插入孩子节点
* @param child
* @param index
*/
void insertChild(Node child, int index) {
System.arraycopy(children, index, children, index + 1, keyNumber - index);
children[index] = child;
}
}这里我采用了静态数组,因此需要多添加一个keyNumber参数来获取有效key的数量,如果使用ArrayList,可以通过size方法获取,因此不需要添加这个属性。
大体框架
public class BTree {
private Node root;
private int t;//最小度数
final int MAX_KEY_NUMBER;//最大key数量
final int MIN_KEY_NUMBER;//最小key数量。用于分裂使用
public BTree(int t) {
this.t = t;
root = new Node(t);
MAX_KEY_NUMBER = 2 * t - 1;
MIN_KEY_NUMBER = 2 * t;
}
static class Node {
boolean leaf = true; //是否是叶子节点
int keyNumber; //有效key
int t; //最小度
int[] keys; // keys数组
Node[] children; //孩子节点数组
public Node(int t) {
this.t = t;
this.keys = new int[2 * t - 1];
this.children = new Node[2 * t];//最大孩子节点个数为为2*t
}
@Override
public String toString() {
return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));
}
/**
* 根据key获取对应节点
*
* @param key
* @return
*/
Node get(int key) {
int i = 0;
while (i < keyNumber) {
//如果在该节点找到,那么直接返回即可
if (keys[i] == key) {
return this;
}
//说明要找的元素可能在children[i]中
if (keys[i] > key) {
break;
}
i++;
}
//如果是叶子节点,直接返回null
if (leaf) {
return null;
}
return children[i].get(key);
}
/**
* 指定位置插入元素
*
* @param key
* @param index
*/
void insertKey(int key, int index) {
System.arraycopy(keys, index, keys, index + 1, keyNumber - index);
keys[index] = key;
keyNumber++;
}
/**
* 向节点中插入孩子节点
*
* @param child
* @param index
*/
void insertChild(Node child, int index) {
System.arraycopy(children, index, children, index + 1, keyNumber - index);
children[index] = child;
}
}
}实现分裂
先说分裂规律,当新增一个节点后使节点中的key满足2t-1,那么该节点就会被分裂。
- 创建一个新的节点,暂时称为right节点(分裂后会在被分裂节点的右边)
- 被分裂节点把 t 以后的 key 和 child 都拷贝到right节点
- t-1 处的 key 插入到 parent 的 index 处,index 指被分裂节点作为孩子时的索引
- right 节点作为 parent 的孩子插入到 index + 1 处
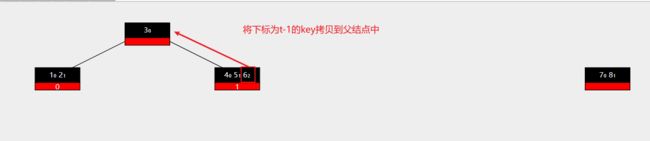
图示如下:
红色部分的意思是当前节点是父结点中作为孩子的下标。黑色部分是key,小数字代表key的下标。
起始存在一个t为3的B树。那么最大key就为 2*3-1 。此时作为父结点孩子下标为1的节点以及存在 4 个key,再添加一个key就会触发分裂。
现在,再添加一个新的key值 8 ,此时到达最大key数,触发分裂
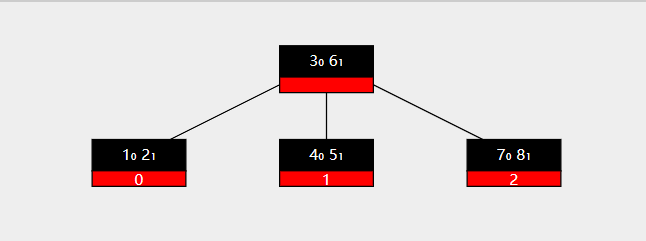
此时分裂结束,分裂后结果如下
具体实现代码如下
private void split(Node parent, int index, Node split) {
if (parent == null) {
//说明分割根节点,除了需要创建right节点之外,还需要创建parent节点
parent = new Node(t);
parent.leaf = false;
parent.insertChild(split, 0);
root = parent;
}
Node right = new Node(t);
//将被分裂节点的一部分key放入right节点中。
System.arraycopy(split.keys, index, right.keys, 0, t - 1);
//新建的节点与被分裂节点在同一层,因此leaf属性应该和被分裂节点一样
right.leaf = split.leaf;
right.keyNumber = t - 1;
//如果被分裂节点不是叶子节点,也需要将孩子节点一并拷贝到right节点中
if (!split.leaf) {
System.arraycopy(split.children, t, right.children, 0, t);
}
split.keyNumber = t - 1;
//将t-1节点放入父结点中
int mid = split.keys[t - 1];
parent.insertKey(mid, index);
parent.insertChild(right, index + 1);
}实现新增
- 首先查找本节点中的插入位置 i,如果没有空位(key 被找到),应该走更新的逻辑。
- 接下来分两种情况
- 如果节点是叶子节点,可以直接插入了
- 如果节点是非叶子节点,需要继续在 children[i] 处继续递归插入
- 无论哪种情况,插入完成后都可能超过节点 keys 数目限制,此时应当执行节点分裂
- 参数中的 parent 和 index 都是给分裂方法用的,代表当前节点父节点,和分裂节点是第几个孩子
具体实现代码如下
public void put(int key) {
doPut(null, 0, root, key);
}
private void doPut(Node parent, int index, Node node, int key) {
int i = 0;
while (i < node.keyNumber && node.keys[i] < key) {
i++;
}
// TODO i实现删除
删除节点会存在下面几种情况
case 1:当前节点是叶子节点,没找到。直接返回null
case 2:当前节点是叶子节点,找到了。直接移除节点即可
case 3:当前节点是非叶子节点,没找到。递归寻找孩子节点是否存在该key
case 4:当前节点是非叶子节点,找到了。找到后驱节点交换key,并将交换后的key删除
case 5:删除后 key 数目 < 下限(不平衡)。需要进行调整
在兄弟节点中keyNumber数量充足的情况下可以通过旋转调整平衡。图示如下
现在要删除节点 2
删除之后,左侧孩子的key数量少于最小限度,因此需要进行一次左旋。
父结点 3 移动到左侧孩子节点中,右侧孩子节点中的第一个key 5 移动到父结点中,左旋结束。
但如果兄弟节点的key数量是最小限度,那么此时应该进行合并,而不是旋转。
合并时,我们通常选择将右侧的节点合并到左侧节点中去。图示如下
此时要删除key 3 ,右侧兄弟节点无法再向被删除节点提供key。
于是将右侧节点移除,同时将父结点的值与被移除节点的值都放在最初的左孩子节点中。
case 6:根节点
当经过合并之后,根结点可能会存在为null的情况,此时让根节点中的 0 号孩子替代掉根节点就好。
具体实现代码如下
/**
* 移除指定元素
*
* @param key
*/
public void remove(int key) {
doRemove(null,root,0, key);
}
private void doRemove(Node parent,Node node,int index, int key) {
//首先要获取指定元素
int i = 0;
while (i < node.keyNumber && node.keys[i] < key) {
i++;
}
if (node.leaf) {
if (node.keys[i] == key) {
//case 2:如果找到了并且是叶子节点
node.removeKey(i);
} else {
//case 1:如果没找到并且是叶子节点
return;
}
} else {
if (node.keys[i] == key) {
//case 4:如果找到了但不是叶子节点
//找到后驱节点并交换位置
Node child = node.children[i + 1];
while (!child.leaf) {
child = child.children[0];
}
int nextKey = child.keys[0];
node.keys[i] = nextKey;
//之所以不直接调用孩子节点的removeKey方法是为了避免删除后发生不平衡
//child.removeKey(0);
doRemove(node,child,i+1, nextKey);
} else {
//case 3:如果没找到但不是叶子节点
doRemove(node,node.children[i],i, key);
}
}
//如果删除后,节点中的key少于下限,那么需要进行调整
if (node.keyNumber < MIN_KEY_NUMBER) {
//平衡调整
balance(parent,node,index);
}
}
/**
* 调整B树
*
* @param parent 父结点
* @param node 被调整节点
* @param index 被调整节点在父结点中的孩子数组下标
*/
private void balance(Node parent, Node node, int index) {
//case 6 根节点
if (node == root) {
if (node.keyNumber==0 && node.children[0]!=null){
root = node.children[0];
}
return;
}
Node leftChild = parent.leftSibling(index);
Node rightChild = parent.rightSibling(index);
//如果左边孩子节点中的key值充足
if (leftChild != null && leftChild.keyNumber > MIN_KEY_NUMBER) {
//将父结点中的key赋值给node
node.insertKey(parent.keys[index - 1], 0);
if (!leftChild.leaf) {
//如果左侧孩子不是一个叶子节点,在旋转过后,会导致keysNumber+1!=children。
//因此将多出来的孩子赋值更多出来一个key的被调整节点
node.insertChild(leftChild.removeRightmostChild(), 0);
}
//将左孩子中最右侧元素赋值给父结点
parent.keys[index - 1] = leftChild.removeRightmostKey();
return;
}
//如果右边充足
if (rightChild != null && rightChild.keyNumber > MIN_KEY_NUMBER) {
node.insertKey(parent.keys[index], node.keyNumber);
if (!rightChild.leaf) {
node.insertChild(rightChild.removeLeftmostChild(), node.keyNumber);
}
parent.keys[index] = rightChild.removeLeftmostKey();
return;
}
//合并
//如果删除节点存在左兄弟,向左合并
if (leftChild != null) {
//将被删除节点从父结点上移除
parent.removeChild(index);
//将父结点的被移除节点的前驱节点移动到左兄弟上
leftChild.insertKey(parent.removeKey(index - 1), leftChild.keyNumber);
node.moveToTarget(leftChild);
} else {
//如果没有左兄弟,那么移除右兄弟节点,并将右兄弟移动到被删除节点上。
parent.removeChild(index+1);
node.insertKey(parent.removeKey(index),node.keyNumber);
rightChild.moveToTarget(node);
}
}完整代码
public class BTree {
private Node root;
private int t;//最小度数
private final int MAX_KEY_NUMBER;
private final int MIN_KEY_NUMBER;
public BTree(int t) {
this.t = t;
root = new Node(t);
MAX_KEY_NUMBER = 2 * t - 1;
MIN_KEY_NUMBER = t-1;
}
static class Node {
boolean leaf = true; //是否是叶子节点
int keyNumber; //有效key
int t; //最小度
int[] keys; // keys数组
Node[] children; //孩子节点数组
public Node(int t) {
this.t = t;
this.keys = new int[2 * t - 1];
this.children = new Node[2 * t];//最大孩子节点个数为为2*t
}
@Override
public String toString() {
return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));
}
/**
* 根据key获取对应节点
*
* @param key
* @return
*/
Node get(int key) {
int i = 0;
while (i < keyNumber) {
//如果在该节点找到,那么直接返回即可
if (keys[i] == key) {
return this;
}
//说明要找的元素可能在children[i]中
if (keys[i] > key) {
break;
}
i++;
}
//如果是叶子节点,直接返回null
if (leaf) {
return null;
}
return children[i].get(key);
}
/**
* 指定位置插入元素
*
* @param key
* @param index
*/
void insertKey(int key, int index) {
System.arraycopy(keys, index, keys, index + 1, keyNumber - index);
keys[index] = key;
keyNumber++;
}
/**
* 向节点中插入孩子节点
*
* @param child
* @param index
*/
void insertChild(Node child, int index) {
System.arraycopy(children, index, children, index + 1, keyNumber - index);
children[index] = child;
}
//移除指定元素
int removeKey(int index) {
int t = keys[index];
System.arraycopy(keys, index + 1, keys, index, --keyNumber - index);
return t;
}
//移除最左边的元素
int removeLeftmostKey() {
return removeKey(0);
}
//移除最右边的元素
int removeRightmostKey() {
return removeKey(keyNumber - 1);
}
//移除指定位置的孩子节点
Node removeChild(int index) {
//获取被移除的节点
Node t = children[index];
//将被移除节点的后面元素向前移动一位
System.arraycopy(children, index + 1, children, index, keyNumber - index);
//将之前最后一位的引用释放
children[keyNumber] = null;
//返回被引用元素
return t;
}
//移除最左边的孩子节点
Node removeLeftmostChild() {
return removeChild(0);
}
//移除最右边的孩子节点
Node removeRightmostChild() {
return removeChild(keyNumber);
}
//移动指定节点到目标节点
void moveToTarget(Node target) {
int start = target.keyNumber;
if (!leaf) {
for (int i = 0; i <= keyNumber; i++) {
target.children[start + i] = children[i];
}
}
for (int i = 0; i < keyNumber; i++) {
target.keys[target.keyNumber++] = keys[i];
}
}
//获取指定孩子节点的左边节点
Node leftSibling(int index) {
return index > 0 ? children[index - 1] : null;
}
//获取指定孩子节点的右边节点
Node rightSibling(int index) {
return index == keyNumber ? null : children[index + 1];
}
}
/**
* 查询key值是否在树中
*
* @param key
* @return
*/
public boolean contains(int key) {
return root.get(key) != null;
}
/**
* 新增节点
*
* @param key
*/
public void put(int key) {
doPut(null, 0, root, key);
}
//index的作用是,给分割方法提供参数
private void doPut(Node parent, int index, Node node, int key) {
//寻找插入位置
int i = 0;
while (i < node.keyNumber && node.keys[i] < key) {
i++;
}
//如果找到了,直接更新
if (node.keys[i] == key) {
return;
}
//如果没找到,查看是否是叶子节点,如果不是,向下寻找
if (node.leaf) {
node.insertKey(key, i);
} else {
doPut(node, i, node.children[i], key);
}
if (isFull(node)) {
split(parent, index, node);
}
}
private boolean isFull(Node node) {
return node.keyNumber == MAX_KEY_NUMBER;
}
/**
* 分裂节点
*
* @param parent
* @param index 分割节点在父结点的孩子下标
* @param split
*/
private void split(Node parent, int index, Node split) {
if (parent == null) {
//说明分割根节点,除了需要创建right节点之外,还需要创建parent节点
parent = new Node(t);
parent.leaf = false;
parent.insertChild(split, 0);
root = parent;
}
Node right = new Node(t);
//将被分裂节点的一部分key放入right节点中。
System.arraycopy(split.keys, t, right.keys, 0, t - 1);
//新建的节点与被分裂节点在同一层,因此leaf属性应该和被分裂节点一样
right.leaf = split.leaf;
right.keyNumber = t - 1;
//如果被分裂节点不是叶子节点,也需要将孩子节点一并拷贝到right节点中
if (!split.leaf) {
System.arraycopy(split.children, t, right.children, 0, t);
for (int i =t;i<=split.keyNumber;i++){
split.children[i]=null;
}
}
split.keyNumber = t - 1;
//将t-1节点放入父结点中
int mid = split.keys[t - 1];
parent.insertKey(mid, index);
parent.insertChild(right, index + 1);
}
/**
* 移除指定元素
*
* @param key
*/
public void remove(int key) {
doRemove(null,root,0, key);
}
private void doRemove(Node parent,Node node,int index, int key) {
//首先要获取指定元素
int i = 0;
while (i < node.keyNumber && node.keys[i] < key) {
i++;
}
if (node.leaf) {
if (node.keys[i] == key) {
//case 2:如果找到了并且是叶子节点
node.removeKey(i);
} else {
//case 1:如果没找到并且是叶子节点
return;
}
} else {
if (node.keys[i] == key) {
//case 4:如果找到了但不是叶子节点
//找到后驱节点并交换位置
Node child = node.children[i + 1];
while (!child.leaf) {
child = child.children[0];
}
int nextKey = child.keys[0];
node.keys[i] = nextKey;
//之所以不直接调用孩子节点的removeKey方法是为了避免删除后发生不平衡
//child.removeKey(0);
doRemove(node,child,i+1, nextKey);
} else {
//case 3:如果没找到但不是叶子节点
doRemove(node,node.children[i],i, key);
}
}
//如果删除后,节点中的key少于下限,那么需要进行调整
if (node.keyNumber < MIN_KEY_NUMBER) {
//平衡调整
balance(parent,node,index);
}
}
/**
* 调整B树
*
* @param parent 父结点
* @param node 被调整节点
* @param index 被调整节点在父结点中的孩子数组下标
*/
private void balance(Node parent, Node node, int index) {
//case 6 根节点
if (node == root) {
if (node.keyNumber==0 && node.children[0]!=null){
root = node.children[0];
}
return;
}
Node leftChild = parent.leftSibling(index);
Node rightChild = parent.rightSibling(index);
//如果左边孩子节点中的key值充足
if (leftChild != null && leftChild.keyNumber > MIN_KEY_NUMBER) {
//将父结点中的key赋值给node
node.insertKey(parent.keys[index - 1], 0);
if (!leftChild.leaf) {
//如果左侧孩子不是一个叶子节点,在旋转过后,会导致keysNumber+1!=children。
//因此将多出来的孩子赋值更多出来一个key的被调整节点
node.insertChild(leftChild.removeRightmostChild(), 0);
}
//将左孩子中最右侧元素赋值给父结点
parent.keys[index - 1] = leftChild.removeRightmostKey();
return;
}
//如果右边充足
if (rightChild != null && rightChild.keyNumber > MIN_KEY_NUMBER) {
node.insertKey(parent.keys[index], node.keyNumber);
if (!rightChild.leaf) {
node.insertChild(rightChild.removeLeftmostChild(), node.keyNumber);
}
parent.keys[index] = rightChild.removeLeftmostKey();
return;
}
//合并
//如果删除节点存在左兄弟,向左合并
if (leftChild != null) {
//将被删除节点从父结点上移除
parent.removeChild(index);
//将父结点的被移除节点的前驱节点移动到左兄弟上
leftChild.insertKey(parent.removeKey(index - 1), leftChild.keyNumber);
node.moveToTarget(leftChild);
} else {
//如果没有左兄弟,那么移除右兄弟节点,并将右兄弟移动到被删除节点上。
parent.removeChild(index+1);
node.insertKey(parent.removeKey(index),node.keyNumber);
rightChild.moveToTarget(node);
}
}
}