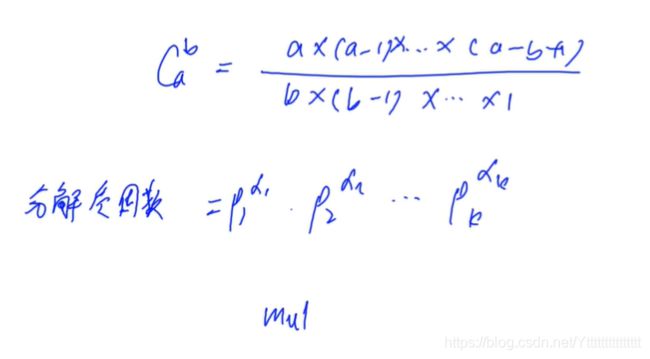算法基础课—数学知识（四）高斯消元、组合数

高斯消元——解方程组

应用：在n的三次方时间内可以解n个方程组的解
方法：矩阵的行列变换
思想：先消元，再回代
最后可以把矩阵变成一个上三角的形式

对于有解和无解的判断

如果0=非零，说明矛盾，肯定无解
如果出现0=0，说明其中一组和某一组表达的意思相同，说明少于n个方程组，求解n个未知数，那肯定存在无穷多组解
在代码中由于出现左侧全0的情况，在每次迭代中，都会被交换到后几行，所以我们只需要对后几行全零的情况进行判断，存在左侧（x1…xn）全0，右侧(b)也等于0，则有解，如果右侧(b)不等于0，则无解

例子

消元

从第一列开始，找到绝对值最大的行，为第二行，和第一行交换

将第一行的第一个数变成1，同一行其他数跟随者按比例缩小或放大。

将下面所有列都置为的第c列都变成0， 则是对该行的按比例放缩，然后相减

对第二列进行操作，找到绝对值最大的那行，不包括第一行，第一行已经固定，然后，将其第一个数变成1，然后依次将后续几列的第一个数变成0.

针对第三列，找到后续绝对值最大的行（不包括前面已经固定的第一行和第二行），然后将第一个数变成1，将下面所有行的第三列变成0，由于不存在之后的列所以不需要这步操作。

回代

将第二行的左侧不是1的x变成0——将第二行-1/3第三行

将第一行的左侧第一个不是1的数变成0,——第一行-0.5第二行

将第一行的左侧第一个不是1的数变成0,——第一行-（-1.5）*第三行

所以最后得到的最后一列即为方程组的解

有无穷多个解的情况

出现如
1 2 0 3
0 2 0 2
1 0 0 1
如果存在某一列都完全是0，则没有关于这一列的信息，消元到最后会变成
1 2 0 3
0 2 0 2
0 0 0 0
此时，可以设置一个数r，在找寻每列绝对值最大的行的时候，如果发现绝对值最大为0，则这一列必定都是0，所以此时r是不叠加的，r用来表示有实际意义的方程个数，显然如果无解r会小于n，所以如果r小于n，且最后一行的b也是0，说明0 = 0，有一个数没有对应方程，则有无穷多个解

无解的情况

出现如
1 2 0 3
0 2 0 2
1 0 0 2
如果存在某一列都完全是0，则没有关于这一列的信息，消元到最后会变成
1 2 0 3
0 2 0 2
0 0 0 1
此时，可以设置一个数r，在找寻每列绝对值最大的行的时候，如果发现绝对值最大为0，则这一列必定都是0，所以此时r是不叠加的，r用来表示有实际意义的方程个数，显然如果无解r会小于n，所以如果r小于n，且最后一行的b不等于0，说明0 = 非0，则有无解。

算法思路

1、 对每n列进行迭代
2、找寻绝对值最大的那一行，如果找到的绝对值最大的那一行的绝对值等于0，说明该列的x没有有效的信息提供，直接continue。
3、如果找到绝对值最大的那一行，则将那一行和最上面的行进行交换（由r控制当前最上面的行）
4、将对应第c列的第r行，进行放缩，将第c列第r行的值放缩到1。即除法，这一行每个数除以第c列第r行的值
5、将后续几行的第c列都变成0，将对应第j行 - 第j行第c列的值* 第r行
6、r ++。表明有效的方程数加1
7、循环结束后，进行回代，从后面的行数开始往上走，j从第i+1列开始
a[i][n] = a[i][n] - a[j][n] * a[i][n]

题目

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

9a504fc2d5628535be9dcb5f90ef76c6a7ef634a.gif

输入格式
第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例：
1.00
-2.00
3.00

代码模板

#include 
#include 
#include 

using namespace std;

const int N = 110;
const double eps = 1e-6;

int n;
double a[N][N];


int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i < n + 1; i ++ ) swap(a[t][i], a[r][i]);
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];

        for (int i = r + 1; i < n; i ++ )
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2;
        return 1;
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[j][n] * a[i][j];

    return 0;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            cin >> a[i][j];

    int t = gauss();

    if (t == 0)
    {
        for (int i = 0; i < n; i ++ ) printf("%.2lf\n", a[i][n]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53389/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

自己的代码

#include 
#include 
using namespace std;
const int N = 1e2 + 10;
double a[N][N];
int n;
void out(){
    int i, j;
    for(i = 0;i < n; i ++){
        for(j = 0; j < n + 1; j ++){
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
     cout<<endl;
}
int guass(){
    int c, i, j, r;
    for(c = 0, r = 0; c < n; c ++){
        int t = r;//设置初始值，r以前是不需要比较的呀
        for(i = r; i < n; i ++){
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        }
        if(fabs(a[t][c]) < 1e-6) continue;
        for(i = 0; i < n + 1; i ++) swap(a[r][i], a[t][i]);
        for(i = n; i >= c; i --) a[r][i] /= a[r][c];//要从后面开始更新，因为除的是前面的数,同时小于c就不用除了，因为都是0
        for(i = r + 1; i < n; i ++){
            if(fabs(a[i][c]) > 1e-6){//即如果其大于0，也就是说，如果本身等于0，就不用操作这一步了，否则会多减，其实不用这一步也可以
                for(j = n; j >= c; j --){
                    a[i][j] -= a[i][c] * a[r][j]; 
                }
            }
        }
        r ++;
    }
    // 回代
    if(r < n){
        for(i = r; i < n; i ++){
            if(a[i][n] > 1e-6) return 3;
        }
        return 2;
    }
    for(i = n - 1; i >= 0; i --){
        for(j = i + 1; j < n; j ++){
            a[i][n] -= a[j][n] * a[i][j]; 
        }
    }
    
    return 1;
}
int main(){
    int i, j;
    cin>>n;
    for(i = 0; i < n; i ++){
        for(j = 0; j < n + 1; j ++){
            cin>>a[i][j];
        }
    }
    int res = guass();
    if(res == 1){
        for(i = 0; i < n; i ++)
            printf("%.2f\n", a[i][n]);
    }
    else if(res == 2) cout<<"Infinite group solutions"<<endl;
    else cout<<"No solution"<<endl;
}

求组合数

方法一

适用于：a, b范围较小的时候，如小于2000
利用公式,递归计算:

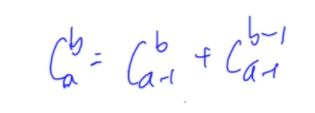
模板

#include 
#include 

using namespace std;

const int N = 2010, mod = 1e9 + 7;


int c[N][N];


void init()
{
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j <= i; j ++ )
            if (!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}


int main()
{
    int n;

    init();

    scanf("%d", &n);

    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);

        printf("%d\n", c[a][b]);
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53393/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

自己的代码

#include
using namespace std;
const int N = 2002, mod = 1e9 + 7;
int c[N][N];
void init(){
    int i, j;
    for(i = 0; i < N; i ++){
        for(j = 0; j <= i; j ++){
            if(!j) c[i][j] = 1;//C(n,0)=1 C(0,0)=1。如果j=0的情况，如果i=0的情况，是都为0.
            else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
        }
    }
}
int main(){
    int i, n, a, b;
    cin>>n;
    init();
    for(i = 0; i < n; i ++){
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
}

方法二

当a和b的范围较大时，如从1-10的5次方
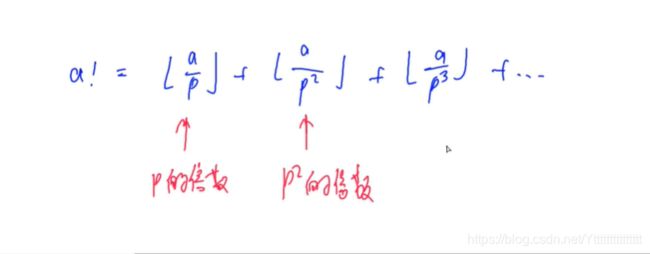
即需要对阶层操作做一个预处理。
这个时候如果用递归的话数据规模就会非常大，所以直接从公式的层面去进行计算。
a的阶层可以直接计算
由于除法本身不满足除余的性质，所以我们把除法转换成乘法，即求他的逆元

于是我们需要
fact[] 数组——记录第i个数的阶乘
infact[]数组——记录第i个数的逆阶乘，即逆元相乘的阶乘

求逆元的方法——由于这里mod题目给的是质数，所以可以用快速幂求逆元，即b ^ (p-2)。

题目

给定 n 组询问，每组询问给定两个整数 a，b，请你输出 Cbamod(109+7) 的值。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组 a 和 b。

输出格式
共 n 行，每行输出一个询问的解。

数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例：
3
3 1
5 3
2 2
输出样例：
3
10
1

模板

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;


int fact[N], infact[N];


int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int main()
{
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++ )
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }


    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53394/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码

#include 
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL fact[N], infact[N];
LL mod = 1e9 + 7;
LL qmi(int a, int k, int p){
    LL res = 1;
    while(k){
        if(k & 1) res = res * a % p;
        a = (LL) a * a % p; 
        k = k >> 1;
    }
    return res;
}
int main(){
    int n, a, b, i;
    cin>>n;
    fact[0] = infact[0] = 1;//0的阶乘和逆阶乘都等于1
    for(i = 1; i < N; i ++){
        fact[i] =  fact[i - 1] * i % mod;
        infact[i] =  infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    for(i = 0; i < n; i ++){
        cin>>a>>b;
        LL res = fact[a] * infact[b] % mod * infact[a - b] % mod;//中间还要除一次余，因为很容易在中间计算的时候溢出
        cout<<res<<endl;
    }
}

方法三

适用于a,b 的范围非常大
卢卡斯定理
思路:将a和b都分别转换成k位p进制，然后分别C（b,a）.。C用逆元的方式求

题目

给定 n 组询问，每组询问给定三个整数 a,b,p，其中 p 是质数，请你输出 Cbamodp 的值。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组 a,b,p。

输出格式
共 n 行，每行输出一个询问的解。

数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,

输入样例：
3
5 3 7
3 1 5
6 4 13
输出样例：
3
3
2

模板

#include 
#include 

using namespace std;

typedef long long LL;


int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b, int p)
{
    if (b > a) return 0;

    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}


int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}


int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        LL a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53399/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码

#include 
using namespace std;
typedef long long LL;
LL qmi(LL a, LL k ,int p){
    LL res = 1;
    while(k){
        if(k & 1) res = res * a % p;
        a = a * a % p;
        k = k >> 1;
    }
    return res;
}
LL C(LL a, LL b, int p){
    int i, j;
    LL res = 1;
    for(i = a, j = 1; i >= a - b + 1; i --, j ++){
        res = res * i % p;
        res = res * qmi(j, p - 2 ,p) % p;
    }
    return res;
}
LL lucas(LL a, LL b, LL p){
    if(a < p && b < p) return C(a, b, p);
    return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;// 要记得除余
}
int main(){
    int n, i, p;
    LL a, b;
    cin>>n;
    for(i = 0; i < n; i ++){
        cin>>a>>b>>p;
        LL res = lucas(a, b, p);
        cout<<res<<endl;
    }
}

方法四

适用于：精度要求较高
如果从高精度运算的话，按照公式是需要做高精度乘法再做高精度除法，而高精度除法较为繁琐，所以我们可以通过先分解质因数，再做高精度乘法。

关键：先分解质因数，再做高精度乘法

求解a的阶乘中有多少个p——即a的阶乘中求解对应p的幂次

题目

输入 a,b，求 Cba 的值。

注意结果可能很大，需要使用高精度计算。

输入格式
共一行，包含两个整数 a 和 b。

输出格式
共一行，输出 Cba 的值。

数据范围
1≤b≤a≤5000
输入样例：
5 3
输出样例：
10

模板

#include 
#include 
#include 

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }

    vector<int> res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53401/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

自己的代码

#include 
#include 
using namespace std;
const int N = 5010;
bool st[N];
int primes[N], sum[N], cnt = 0;
void getprimes(int n){
    int i, j;
    for(i = 2; i <= n; i ++){
        if(!st[i]) primes[cnt++] = i;
        for(j = 0; primes[j] <= n / i; j ++){
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int get(int n, int p){
    int res = 0;
    while(n){
        res += n / p;
        n /= p;
    }
    return res;
}
vector<int> mul(vector<int> a, int b){
    vector<int> c;
    int t = 0, i;
    for(i = 0; i < a.size(); i ++){
        t += a[i] * b;
        c.push_back(t % 10);
        t = t / 10;
    }
    while (t)//这里注意改成while t，对t进行处理，和加法不同的是，加法最后得t只可能为个位数，而乘法这里有可能为两位数
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}
int main(){
    int a, b, i, j, p;
    cin>>a>>b;
    
    getprimes(a);
    for(i = 0; i < cnt; i ++){
        p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }
    vector<int> res;
    res.push_back(1);
    for(i = 0; i < cnt; i ++){
        for(j = 0; j < sum[i]; j ++){
            res = mul(res, primes[i]);
        }
    }
    for(i = res.size() - 1; i >= 0; i --)
        cout<<res[i];
}

满足条件的01序列

题目

给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

输出的答案对 109+7 取模。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示答案。

数据范围
1≤n≤105
输入样例：
3
输出样例：
5

卡特兰数

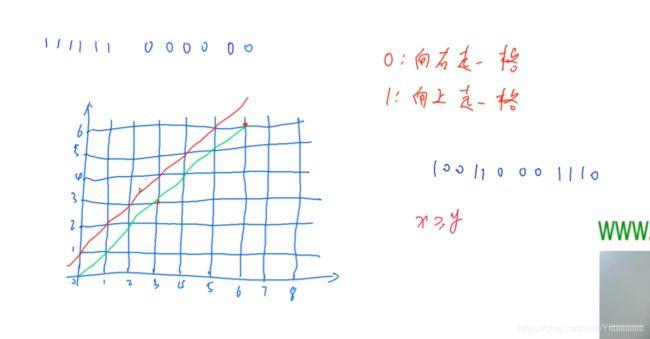
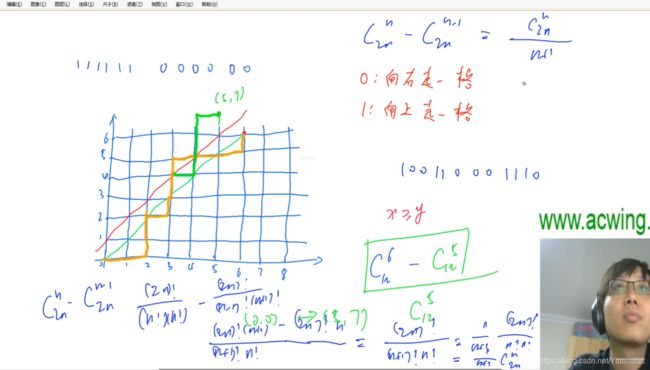
任意一个0,1序列可转换成如下图所示的图，任意一个路径也可以转换对应的01序列

根据题目
所以我们所有的点都应该在这个红色这条边的下面

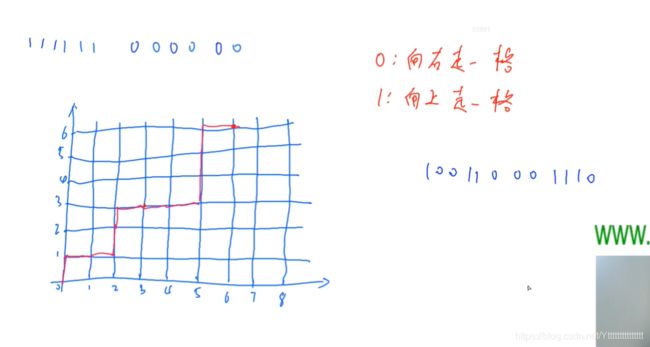
思路：任何一条从（0,0 ）走到（6,6）且经过红边的路径，我们将其到达红边的那个点关于红线做轴对称，会到达（5,7），变成一条从（0,0）走到（5,7）的路径。我们可以发现任意一条从（0,0）走到（5,7）的路径一定经过红线，所以我们对经过红线的点之后做轴对称，一定是一条从（0,0 ）走到（6,6）且经过红边的路径，所以那些不符合条件的数量就是C 5 12。

卡特兰数的推导

公式在右上角

对应组合数的第二种方法，用a，b的范围较大，所以先进行一步预处理，同时很多思想都把除法转换成逆元的形式。

模板

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;


int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int main()
{
    int n;
    cin >> n;

    int a = n * 2, b = n;
    int res = 1;
    for (int i = a; i > a - b; i -- ) res = (LL)res * i % mod;

    for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;

    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;

    cout << res << endl;

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/53407/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码

#include
using namespace std;
typedef long long LL;
int mod = 1e9 + 7;
int qmi(int a, int k, int p){
    int res = 1;
    while(k){
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k = k >> 1;
    }
    return res;
}
int main(){
    int n, i;
    cin>>n;
    int res = 1;
    int a = 2*n, b = n;
    for(i = a; i >= a - b + 1; i --) res = (LL)res * i % mod;
    for(i = 1; i <= b; i ++) res = (LL)res * qmi(i, mod - 2, mod) % mod;
    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;//注意每次乘法中要转换成ll，因为可能溢出，或者将变量类型设置为ll也可以
    cout<<res<<endl;
}