2312、卖木头块 | 面试官与狂徒张三的那些事(leetcode,附思维导图 + 全部解法)
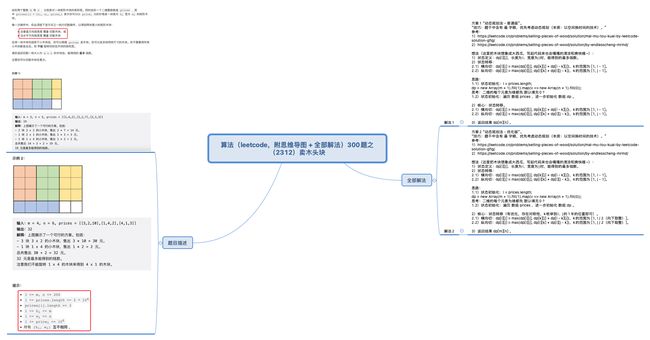
零 标题:算法(leetcode,附思维导图 + 全部解法)300题之(2312)卖木头块
一 题目描述
二 解法总览(思维导图)
三 全部解法
面试官:看你准备得差不多了,我们开始面试吧。
狂徒张三:okk~
面试官:题目看得差不多了的话,来说说你的想法、思路哈~
狂徒张三:因为题目中,含有 “最” 字眼,所以我觉得应该优先考虑使用 “动态规划” 。
面试官: 那你觉得使用动态规划的条件有哪些呢?
狂徒张三:我个人认为,应该需要具备2个条件:
1)最优子结构
2)无后效性
面试官: 很好,那你知道动态规划的本质和解题步骤分别是什么吗?
狂徒张三:
1)本质:一种以空间换时间的技术
2)解题步骤:分3步。状态定义: 每个状态的决策,存放每个状态的变量;状态转移方程: 当前状态与之前状态之间的转换关系;初始状态: 初始的状态或者边界条件等。
面试官:小伙子,可以呀。我看你也差不多热完身了,那你就用如上知识解下这道题吧~
旁白:过了5-10分钟,张三迟迟写不出代码。
面试官:(一脸凝重、困惑)难道你只背了相关概念,没进行过相关题目的编码吗?
狂徒张三:(张三面漏怯色)额。。。。
面试官:这样,你把木块想象成大西瓜,写起代码来也会嘎嘎的清凉和爽快哦~
那题目就变成了 —— 你有1个二维(长度为w、宽度为h)的大西瓜,你可以选择直接把它卖掉(若此时得有人正好买长度为w、宽度为h),不然的话此时的大西瓜只能获得0元
狂徒张三:对的,然后我们也可以选择不卖此时的大西瓜,进行横向、纵向的切瓜,把大西瓜不断切成不同的小西瓜,最后从这些切瓜方案中计算出当前大西瓜的能卖处的最大价钱。
面试官:是的,那你这边根据之前所说,写下 状态定义 和 状态转移方程吧~
狂徒张三:好的。
我理解的状态定义 —— dp[i][j],长度为i、宽度为j时,能得到的最多钱数。
状态转移方程 —— 横向切瓜时:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i - 1]。
纵向切瓜时:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j - 1]。
面试官:那状态的初始化呢?
狂徒张三:根据数组 prices ,进行初始化 —— 当 i、j 存在于 prices 里的0、1下标位置上时,dp[i][j] = prices[对应的元素下标][2]。
面试官:很好,既然思路已经理清了,那就开始你的表演,啊不、开始你的代码编写吧~

旁边:张三瞬间如同任督二脉被打通,三下五除二,不到10分钟便把代码敲打了出来~
1 方案1
1)代码:
// 方案1 “动态规划法 - 普通版”。
// “技巧:题干中含有 最 字眼,优先考虑动态规划(本质:以空间换时间的技术)。”
// 参考:
// 1)https://leetcode.cn/problems/selling-pieces-of-wood/solution/mai-mu-tou-kuai-by-leetcode-solution-gflg/
// 2)https://leetcode.cn/problems/selling-pieces-of-wood/solution/by-endlesscheng-mrmd/
// 想法(这里把木块想象成大西瓜,写起代码来也会嘎嘎的清凉和爽快哦~):
// 1)状态定义:dp[i][j],长度为i、宽度为j时,能得到的最多钱数。
// 2)状态转移:
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i - 1]。
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j - 1]。
// 思路:
// 1.1)状态初始化:l = prices.length;
// dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 思考:二维的每个元素为啥都先 默认填充0 ?
// 1.2)状态初始化:遍历 数组 prices ,进一步初始化 数组 dp 。
// 2)核心:状态转移。
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i - 1]。
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j - 1]。
// 3)返回结果 dp[m][n] 。
var sellingWood = function(m, n, prices) {
// 1.1)状态初始化:l = prices.length;
// dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 思考:二维的每个元素为啥都先 默认填充0 ?
const l = prices.length;
let dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 1.2)状态初始化:遍历 数组 prices ,进一步初始化 数组 dp 。
for (let i = 0; i < l; i++) {
const [width, height, price] = prices[i];
dp[width][height] = price;
}
// 2)核心:状态转移。
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i - 1]。
for (let k = 1; k < i; k++) {
dp[i][j] = Math.max(dp[i][j], dp[k][j] + dp[i - k][j]);
}
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j - 1]。
for (let k = 1; k < j; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[i][j - k]);
}
}
}
// 3)返回结果 dp[m][n] 。
return dp[m][n];
};
2 方案2
面试官:Good。代码结构很有层次感,注释也放在了很合适的位置~
狂徒张三:毕竟这个“二维的大西瓜”是保熟的,我敢保证这里的算法一定是最优的,能够保证我们的大西瓜卖出最高的价钱。
面试官:你确定你这个“大西瓜切割算法”保熟吗?我看不一定吧?

狂徒张三:我是1个正经的算法人,还能给你写法“生瓜算法”不成?
面试官:我问你,这“大西瓜切割算法”保熟吗?
狂徒张三:你就说我这次面试能不能过吧~
面试官:
狂徒张三:那我在看看、想想优化点吧
旁白:只见张三在纸上齐飕飕的写起了代码运行过程。
…
dp[5][5] = max(dp[5][5], dp[1][5] + dp[4][5], dp[2][5] + dp[3][5], dp[3][5] + dp[2][5], dp[2][5] + dp[1][5])
…
狂徒张三:看起来确实有优化点 —— 存在大量的冗余计算,我们下标k只需枚举到一半的位置即可 —— 即 k的范围为 [1, i / 2(向下取整)] 。
1)代码:
// 方案2 “动态规划法 - 优化版”。
// “技巧:题干中含有 最 字眼,优先考虑动态规划(本质:以空间换时间的技术)。”
// 参考:
// 1)https://leetcode.cn/problems/selling-pieces-of-wood/solution/mai-mu-tou-kuai-by-leetcode-solution-gflg/
// 2)https://leetcode.cn/problems/selling-pieces-of-wood/solution/by-endlesscheng-mrmd/
// 想法(这里把木块想象成大西瓜,写起代码来也会嘎嘎的清凉和爽快哦~):
// 1)状态定义:dp[i][j],长度为i、宽度为j时,能得到的最多钱数。
// 2)状态转移:
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i - 1]。
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j - 1]。
// 思路:
// 1.1)状态初始化:l = prices.length;
// dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 思考:二维的每个元素为啥都先 默认填充0 ?
// 1.2)状态初始化:遍历 数组 prices ,进一步初始化 数组 dp 。
// 2)核心:状态转移(有优化,存在对称性,k枚举到i、j的1半的位置即可)。
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i / 2(向下取整)]。
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j / 2(向下取整)]。
// 3)返回结果 dp[m][n] 。
var sellingWood = function(m, n, prices) {
// 1.1)状态初始化:l = prices.length;
// dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 思考:二维的每个元素为啥都先 默认填充0 ?
const l = prices.length;
let dp = new Array(m + 1).fill(1).map(v => new Array(n + 1).fill(0));
// 1.2)状态初始化:遍历 数组 prices ,进一步初始化 数组 dp 。
for (let i = 0; i < l; i++) {
const [width, height, price] = prices[i];
dp[width][height] = price;
}
// 2)核心:状态转移。
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 2.1)横向切:dp[i][j] = max(dp[i][j], dp[k][j] + dp[i - k][j]),k的范围为 [1, i / 2(向下取整)]。
for (let k = 1; k <= Math.floor(i / 2); k++) {
dp[i][j] = Math.max(dp[i][j], dp[k][j] + dp[i - k][j]);
}
// 2.2)纵向切:dp[i][j] = max(dp[i][j], dp[i][k] + dp[i][j - k]),k的范围为 [1, j / 2(向下取整)]。
for (let k = 1; k <= Math.floor(j / 2); k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[i][j - k]);
}
}
}
// 3)返回结果 dp[m][n] 。
return dp[m][n];
};
旁白:张三写完了如上代码,急忙问面试官。
狂徒张三:通过面试了吧?
狂徒张三:

又1个offer,然后马上就要出任 CEO 了,我晚上应该是去吃 沙县小吃 呢? 还是 兰州拉面 呢?哎,选择太多也是一种烦恼!
四 资源分享 & 更多
1 历史文章 - 总览
| 文章名称 | 解法 | 阅读量 |
|---|---|---|
| 1. 两数之和(Two Sum) | 共 3 种 | 2.7 k+ |
| 2. 两数相加 (Add Two Numbers) | 共 4 种 | 2.7 k+ |
| 3. 无重复字符的最长子串(Longest Substring Without Repeating Characters) | 共 3 种 | 2.6 k+ |
| 4. 寻找两个正序数组的中位数(Median of Two Sorted Arrays) | 共 3 种 | 2.8 k+ |
| 5. 最长回文子串(Longest Palindromic Substring) | 共 4 种 | 2.8 k+ |
| 6. Z 字形变换(ZigZag Conversion) | 共 2 种 | 1.9 k+ |
| 7. 整数反转(Reverse Integer) | 共 2 种 | 2.4 k+ |
| 8. 字符串转换整数 (atoi)(String to Integer (atoi)) | 共 3 种 | 4.2 k+ |
| 9. 回文数(Palindrome Number) | 共 3 种 | 4.3 k+ |
| 11. 盛最多水的容器(Container With Most Water) | 共 5 种 | 4.0 k+ |
| 12. 整数转罗马数字(Integer to Roman) | 共 3 种 | 3.2 k+ |
| 13. 罗马数字转整数(Roman to Integer) | 共 3 种 | 3.8 k+ |
| 14. 最长公共前缀(Longest Common Prefix) | 共 4 种 | 3.0 k+ |
| 15. 三数之和(3Sum) | 共 3 种 | 60.7 k+ |
| 16. 最接近的三数之和(3Sum Closest) | 共 3 种 | 4.7 k+ |
| 17. 电话号码的字母组合(Letter Combinations of a Phone Number) | 共 3 种 | 3.1 k+ |
| 18. 四数之和(4Sum) | 共 4 种 | 11.5 k+ |
| 19. 删除链表的倒数第 N 个结点(Remove Nth Node From End of List) | 共 4 种 | 1.2 k+ |
| 20. 有效的括号(Valid Parentheses) | 共 2 种 | 1.8 k+ |
| 21. 合并两个有序链表(Merge Two Sorted Lists) | 共 3 种 | 1.2 k+ |
| 22. 括号生成(Generate Parentheses) | 共 4 种 | 1.1 k+ |
| 23. 合并K个升序链表(Merge k Sorted Lists) | 共 4 种 | 0.9 k+ |
| 24. 两两交换链表中的节点(Swap Nodes in Pairs) | 共 3 种 | 0.5 k+ |
| 25. K 个一组翻转链表(Reverse Nodes in k-Group) | 共 5 种 | 1.3 k+ |
| 26. 删除有序数组中的重复项(Remove Duplicates from Sorted Array) | 共 4 种 | 1.3 k+ |
| 27. 移除元素(Remove Element) | 共 4 种 | 0.4 k+ |
| 28. 实现 strStr()(Implement strStr()) | 共 5 种 | 0.8 k+ |
| 29. 两数相除(Divide Two Integers) | 共 4 种 | 0.6 k+ |
| 30. 串联所有单词的子串(Substring with Concatenation of All Words) | 共 3 种 | 0.6 k+ |
| 31. 下一个排列(Next Permutation) | 共 2 种 | 0.8 k+ |
| 32. 最长有效括号(Longest Valid Parentheses) | 共 2 种 | 1.4 k+ |
| 33. 搜索旋转排序数组(Search in Rotated Sorted Array) | 共 3 种 | 1.0k+ |
| 34. 在排序数组中查找元素的第一个和最后一个位置(Find First and Last Position of Element in Sorted Array) | 共 3 种 | 0.5 k+ |
| 35. 搜索插入位置(Search Insert Position) | 共 3 种 | 0.3 k+ |
| 36. 有效的数独(Valid Sudoku) | 共 1 种 | 0.6 k+ |
| 38. 外观数列(Count and Say) | 共 5 种 | 1.1 k+ |
| 39. 组合总和(Combination Sum) | 共 3 种 | 1.4 k+ |
| 40. 组合总和 II(Combination Sum II) | 共 2 种 | 1.6 k+ |
| 41. 缺失的第一个正数(First Missing Positive) | 共 3 种 | 1.2 k+ |
| 53. 最大子数组和(Maximum Subarray) | 共 3 种 | 0.3k+ |
| 88. 合并两个有序数组(Merge Sorted Array) | 共 3 种 | 0.4 k+ |
| 102. 二叉树的层序遍历(Binary Tree Level Order Traversal) | 共 3 种 | 0.4 k+ |
| 146. LRU 缓存(LRU Cache) | 共 2 种 | 0.5 k+ |
| 160. 相交链表(Intersection of Two Linked Lists) | 共 2 种 | 0.1 k+ |
| 200. 岛屿数量(Number of Islands) | 共 4 种 | 0.1 k+ |
| 206. 反转链表(Reverse Linked List) | 共 3 种 | 1.0 k+ |
| 215. 数组中的第K个最大元素(Kth Largest Element in an Array) | 共 3 种 | 0.5 k+ |
| 236. 二叉树的最近公共祖先(Lowest Common Ancestor of a Binary Tree) | 共 3 种 | 0.1 k+ |
| 2119. 反转两次的数字(A Number After a Double Reversal) | 共 2 种 | 0.3 k+ |
| 2120. 执行所有后缀指令(Execution of All Suffix Instructions Staying in a Grid) | 共 1 种 | 0.4 k+ |
| 2124. 检查是否所有 A 都在 B 之前(Check if All A’s Appears Before All B’s) | 共 4 种 | 0.4 k+ |
| 2125. 银行中的激光束数量(Number of Laser Beams in a Bank) | 共 3 种 | 0.3 k+ |
| 2126. 摧毁小行星(Destroying Asteroids) | 共 2 种 | 1.6 k+ |
| 2129. 将标题首字母大写(Capitalize the Title) | 共 2 种 | 0.6 k+ |
| 2130. 链表最大孪生和(Maximum Twin Sum of a Linked List) | 共 2 种 | 0.6 k+ |
| 2133. 检查是否每一行每一列都包含全部整数(Check if Every Row and Column Contains All Numbers) | 共 1 种 | 0.6 k+ |
2 博主简介
码农三少 ,一个致力于编写 极简、但齐全题解(算法) 的博主。
专注于 一题多解、结构化思维 ,欢迎一起刷穿 LeetCode ~