经典递归分治问题——汉诺塔

递归算法总体思想

先将一个大问题逐步分解成小问题，直到满足条件，最后将这些小问题又自底向上逐步求出原问题的解。

问题描述

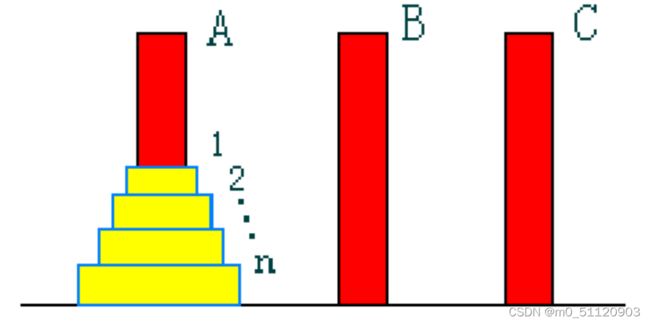
设a,b,c是3个塔座。开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1,2.... , n,现要求将塔座a上的这一叠圆盘移到塔座b上，并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则1:每次只能移动1个圆盘;
规则2:任何时刻都不允许将较大的圆盘压在较小的圆盘之上
规则3:在满足移动规则1和2的前提下，可将圆盘移至a，b，c任一个塔上

问题分析

注意：在这里面，a是源塔，即圆盘最开始在的位置，b是目标塔，即最终结果圆盘所在的位置，c是辅助塔，用来在满足规则的情况下移动圆盘而进行辅助的塔

开始时，圆盘和塔的状况

代码解读

 先抛出代码，再根据代码来理解递归过程

public class Hanoi {
    public static void main(String[] args){
        int n=4;
        char a = 'A',b = 'B',c = 'C';
        hanoi(4,a,b,c);
    }

    //n是圆盘的数目，a是源塔，b是目标塔，c是辅助塔

    public static void hanoi(int n,char a,char b,char c){
        if(n>0){
            hanoi(n-1,a,c,b);
            move(n,a,b);
            hanoi(n-1,c,b,a);
        }
    }
    public static void move(int n,char a,char b){
        System.out.println("把第"+n+"个盘子从"+a+"移动到"+b);
    }
}

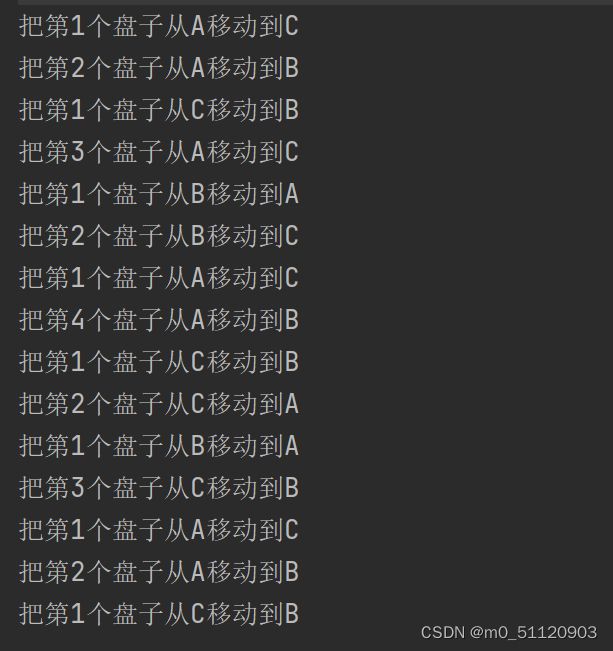
其输出结果是

首先，我们看主要代码，就是实现递归解决汉诺塔的问题的代码

    //a是源塔，b是目标塔，c是辅助塔

    public static void hanoi(int n,char a,char b,char c){
        if(n>0){
            hanoi(n-1,a,c,b);
            move(n,a,b);
            hanoi(n-1,c,b,a);
        }
    }

这里是定义了函数hanoi，在代码内部，我们看到它自身又调用了自己，这就是递归，间接或直接的调用自身。

注意：hanoi()函数里面a，b，c以及move()里的a，b，c的位置都是有讲究的

给出一个通用公式就是（一般将前面的源塔和目标塔定好后，后面的辅助塔就是出去这两个之外的一个）：

hanoi（圆盘数n，源塔0，目标塔0，辅助塔0）{

        if（圆盘数n > 0）{

                hanoi（前n-1个圆盘数，源塔1，目标塔1，辅助塔1）

                move（n，源塔0，目标塔0）

                hanoi（前n-1个圆盘数，目标塔1，目标塔0，源塔1）

        }

}

 如何理解？

现在用一个具体例子来说明它的调用过程。

例如，n=4，即圆盘有4个，按照从上到下，从小到大的顺序放置在a塔上。现在执行hanoi函数，

通过if条件判断知道，4>0，执行if语句内的代码；

执行hanoi(n-1,a,c,b)，即将a塔上，上面的a-1个圆盘移到c塔上，在该例中是将上面3个圆盘从a移到c上（可以发现它没有满足规则1，一次移动一个，因此这部分还要继续划分成小问题，直到只剩下一个圆盘，即n==0），后面的b可以不用管，但是一定要写上。注意：这里一定要执行完hanoi这个函数才会出来继续执行下一步的move函数；这也是将大问题划分为许多同类小问题的过程

那么hanoi(4-1,a,c,b)这部分代码是怎么执行的呢？将它不展现出来的过程写出来是这样的

在n>0的时候，代码都不会真正输出，一下代码部分都是逻辑实现过程，代码上不会真正写，它都已经包含在递归调用里面了，这也是递归的优点，省去了繁琐的步骤。只有n==0，也就是划分到了最小的子问题，才会输出。

//对于这部分来说，a是源塔，c是目标塔，只要记住第一个参数是源塔，
//第二个是目标塔，这和自己的设定有关，也可以将第三个参数设定为目标塔
//那么对于这部分来说，要实现将3个圆盘满足三条规则的情况下从a移到c上
//首先将前2个整体移到b上，然后将a上剩余的第3个圆盘从a上移到目标塔c上
//再将之前移到b上的整体又整体的移到c上
//但是整体移动依旧不满足规则，于是又要将它细分子问题
hanoi(3,a,c,b){
    if(3>0){
        hanoi(2,a,b,c);
        move(3,a,c);
        hanoi(2,b,c,a);
    }
}

同理，在这里也调用了自身hanoi(2,a,b,c)，代码执行原则：一定要将函数里面的全部执行完，才可以继续下一步，因此这里也不进入move(3,a,c)的执行，而是将hanoi(2,b,c,a)执行完，它的执行过程是

//
hanoi(2,a,b,c){
    if(2>0){
        hanoi(1,a,c,b);
        move(2,a,b);
        hanoi(1,c,b,a);
    }
}

//
hanoi(1,a,c,b){
    if(1>0){
        //到达这里的时候，执行hanoi(0,a,b,c)会发现不满足0>0的条件，
        //因此不会再继续执行该部分
        //而是执行下一步move(1,a,c),开始真正的在屏幕上输出
        //这里输出的是“将第1个圆盘从a移到c上”
        //与输出结果的第一句话对应
        hanoi(0,a,b,c);
        move(1,a,c);
        hanoi(0,b,c,a);
    }
}

走到这里，移动4个圆盘的大问题已经把所有的子问题划分完了，现在开始自底向上逐步求出原来的解。

我们已经输出了最小子问题的解了，即hanoi(1,a,c,b)执行完，继续向上走，发现执行完hanoi(1,a,c,b)后应当执行move(2,a,b)，于是屏幕输出“将第2个圆盘从a移动到b”；

执行完move(2,a,b)后，应当执行hanoi(1,c,b,a)，可以看出应当输出“将第1个圆盘从c移动到b上”

hanoi(1,c,b,a){
    if(1>0){
        hanoi(0,c,a,b);
        move(1,c,b);
        haoni(0,a,b,c);
    }
}

剩下过程同理