用数组实现的二叉树(C++实现)
本文所用方法同样适用于完全二叉树的构建
目录
前言
一、前置知识
深度为k的二叉树至多节点
具有n个节点的完全二叉树的深度
关于左右孩子和双亲节点的推导
二、代码时间
1.前期准备
2.函数部分
构造空二叉树
查询树的深度
返回某位置结点的值
对某位置结点赋值
查询非根结点的双亲
逐层,按本层序号输出二叉树
其他
前言
刚学没多久,怕忘了,就贴在这了
一、前置知识
###如不了解满二叉树/完全二叉树请移步其他文章,本文略过不表###
###本文编号均按本树在同深度的满二叉树上的编号进行标记###
-
深度为k的二叉树至多有
 个节点
个节点
(深度为k就是指有k层的二叉树)
其实这个值就是深度为k的满二叉树的结点数,注意不是完全二叉树,他们并不一样。
-
具有n个节点的完全二叉树的深度为
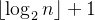
![]() 的意思是向下取不大于x的最大整数
的意思是向下取不大于x的最大整数
其实满二叉树就是一种特殊的完全二叉树,特殊就在于满二叉树所有的叶子节点都在同一层,因此是“满”的。前文已经提到满二叉树的节点是![]() ,那么倒推一下k的值,可以得到
,那么倒推一下k的值,可以得到![]()
![]()
-
关于左右孩子和双亲节点的推导
对于一颗有n个结点的完全二叉树(深度为![]() )的节点按层序编号(从第1层到底
)的节点按层序编号(从第1层到底![]() 层,每层从左往右),对于任意结点(
层,每层从左往右),对于任意结点(![]() )有:
)有:
- 如果
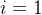 ,则结点
,则结点 是二叉树的根,无双亲;如果
是二叉树的根,无双亲;如果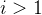 ,其双亲是结点
,其双亲是结点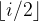 。
。 - 如果
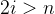 ,则结点
,则结点 是叶子结点(没有左孩子);否则其左孩子是结点
是叶子结点(没有左孩子);否则其左孩子是结点 。
。 - 如果
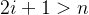 ,则结点
,则结点 是叶子结点(没有右孩子);否则其右孩子是结点
是叶子结点(没有右孩子);否则其右孩子是结点 。
。
本文所用的实现方法在完全二叉树上空间利用效率最高,普通二叉树可模拟完全二叉树,将与同深度满二叉树相比,不存在的结点设置为某个约定值即可
二、代码时间
1.前期准备
主要是头文件和自定义一些数据类型
#include
using std::cout;//此处不选择using namespace std
//是防止出现变量名冲突
const int MAX_SIZE=100;//储存空间初始长度
const int MAX_TREE_SIZE=100;//二叉树最大节点数
const int Nil=0;//二叉树初值
//函数状态码(此处我使用了枚举,其实bool也可以的)
typedef enum{
ERROR=0,OK=1
}Status;
typedef int TElem_type;//树节点的数据类型
typedef TElem_type SqBi_tree[MAX_TREE_SIZE];//下标0的元素储存根节点
typedef struct
{
int level;//层
int order;//本层(在满二叉树上的)序号
}Position; 简单实现一下pow(主要是考虑到自带的pow是double的,可能稍慢,实际上不需要处理int外的数据)
int pow(int x,int y)
{
int a=1;
for(int i=0;i2.函数部分
-
构造空二叉树
//构造空二叉树T(T是固定数组,不会改变,不需要引用)
Status Tnit_biTree(SqBi_tree T)
{
//其实C++全局数组默认0 这个函数纯纯为了配套
for(int i=0;i-
查询树的深度
//查询树的深度
int BiTree_depth(SqBi_tree T)
{
int i,j;
for(i=MAX_TREE_SIZE-1;i>=0;i--)//找到(按满二叉树计算)序号最大的那个节点
if(T[i]!=Nil)
break;
i++;
do{
j++;
}while(i>=pow(2,j));//[具有n个节点的完全二叉树的深度是: log以2为底n为真数 向下取整+1]
return j;
}-
返回某位置结点的值
//返回处于位置e(指某个节点的层,本层序号)的节点的值
TElem_type Value(SqBi_tree T,Position e)
{
return T[pow(2,e.level-1)+e.order-2];
}-
对某位置结点赋值
Status Assign(SqBi_tree T,Position e,TElem_type value)
{
int i=Value(T,e);//将层,本层序号转化为矩阵序号
if(value!=Nil && T[i/2]==Nil)//给叶子节点赋非空值但双亲为空
//[对于i>1的节点,双亲节点的位置是i/2]
return ERROR;
else if (value==Nil && (T[i*2+1]!=Nil||T[i*2+2]!=Nil))//给双亲赋空值但叶子不为空
return ERROR;
T[i]=value;
return OK;
}-
查询非根结点的双亲
//若e是T的非根节点,返回e的双亲值,否则返回nil
TElem_type Parent(SqBi_tree T,TElem_type e)
{
if(T[0]==Nil)//空树
return ERROR;
for(int i=1;i-
逐层,按本层序号输出二叉树
void Print(SqBi_tree T)
{
Position p;
TElem_type e;
for(int j=1;j<=BiTree_depth(T);j++)
{
cout<<"第"<其他
小白第一次写博客,如有疏漏还请君不吝赐教