全面(16万字)深入探索深度学习:基础原理到经典模型网络的全面解析
前言
Stacking(堆叠)
网页调试
- 学习率:它决定了模型在每一次迭代中更新参数的幅度
- 激活函数-更加详细
激活函数的意义:
激活函数主要是让模型具有非线性数据拟合的能力,也就是能够对非线性数据进行分割/建模如果没有激活函数:
第一个隐层: lrl 0: z0=1.2*x1+0.12*x2+2.1 h0=z0 Irl1:z1=0.58*x1-0.96*x2-2.0 h1=z1 lr1 2: z2=0.51*x1+ 1.1*x2-2.2 h2 =z2 输出层: lr2: m=2.1*h0-2.3*h1-2.4 h2=z2 整合一下: m=2.1*(1.2*x1+0.12*x2+-2.1)- 2.3*(0.58*x1--0.96*x2-2.0)- 2 .4*(0.51*x1+1.1*x2-2.2) m=(2.1*1.2-.2.3*0.58.-.2.4*0.51)*x1+ (2.1*0.12.+.2.3*0.96.--2.4*1.1) *x2+ (2.1*2.1+.2.3*2.0.+.2.4*2.2)
正则化:L1,L2
正则化系数
问题类型:分类,回归
第一步:学习L个学习器,这里假定L个学习器都是逻辑回归LR模型
NOTE:实际情况下,L个学习器可以是不同模型算法的
第二步:学习元模型,这里假定元模型也是逻辑回归IR模型
Stackinq缺点:
- 学习器和元模型之间的训练是完全独立的,也就是两个阶段的训练没有影响
- 在训练的时候,实际上数据是进行划分的
多项式扩展 + LR:
原始:
特征属性: x1、x2、x3
目标属性: y
LR预测函数: p = sigmoid(w1x1+w2x2+w3*x3)
二阶的多项式扩展:特征属性: x1、x2、x3、x1*x2、x1*x3、x2*x3、x1^2、x2^2、x3^2 目标属性: y LR预测函数: p = sigmoid(w1*x1 + w2*x2 + w3*x3 + w4*x1*x2 + w5*x1*x3 + w6*x2*x3 + w7*x1^2 + w8*x2^2 + w9*x3^2)多项式扩展相当于将坐标系做了一个转换,是从低维到高维的一个映射
多项式扩展就相当于是一种映射函数(理解成神经元的功能)
z1=f1(x1,x2,x3)=x1 z2=f2(x1,x2,x3)=x2 z3=f3(x1,x2,x3)=x3 z4=f4(x1,x2,x3)=x1*x2 z5=f5(x1,x2,x3)=x1*x3 z6=f6(x1,x2,x3)=x2*x3 z7=f7(x1,x2,x3)=x1^2 z8=f8(x1,x2,x3)=x2^2 z9=f9(x1,x2,x3)=x3^2 NOTE: 多项式扩展是不是就是将原始的特征属性(x1,x2,x3); 通过映射函数(神经元)映射到(z1,z2,z3,z4,z5,z6,z7,z8,z9)后,就会发现原来线性不可分的数据变成了线性可分
深度学习/神经网络
可以看出是stacking的进一步的发展,和stacking相比,主要的不同点在于:
- 深度学习中各个层次之间是相互影响的、互相促进的
- 全量数据均参与整个模型的训练
- 深度学习中各个子学习器以及元模型全部都是同结构的逻辑回归IR模型(线性回归模型+激活函数)
步骤理解一下:
第一个隐层: lr1_0: z0 =1.2*x1+0.12*x2+2.1 h0 =sigmoid (z0) lr1_1: z1=0.58*x1-0.96*x2--2.0 hl=-sigmoid (z1) lr1_2: z2 = 0.51*x1+1.1*x2-2.2 h2 = sigmoid (z2) 输出层: lr2: m=2.1*h0 -2.3*h1-2.4*h2 p = sigmoid (m) pred_y =1 if p >= 0.5 else 0 <===> pred_y =1 if m >= 0 else 0NOTE:
真正输出的时候不需要做sigmoid转换每个神经元的功能就是提取特征信息,对每个样本而言每个神经元(每组参数)相当于从某个方面进行特征的描述
深度学习:维度=通道数
深度学习花书读书笔记目录 - 知乎 (zhihu.com)
深度神经网络(Deep Neural Networks,DNN)
文章目录
- 前言
-
- Stacking(堆叠)
- 深度学习/神经网络
- **深度神经网络**(Deep Neural Networks,DNN)
-
- 几个重要问题
-
- 深度学习和神经网络的关系
- 什么是神经网络
- 神经网络如何进行学习
-
- 向量化操作
- 损失函数
- 学习率退火(learning rate annealing)
- 为什么神经网络用到梯度下降优化方法
- 梯度消失和梯度爆炸
-
- 梯度消失和梯度爆炸
- 梯度消失、爆炸的解决方案
-
- 预训练和微调
- 梯度剪切、正则
- relu、leakyrelu、elu等激活函数
- Batch Normalization(批规范化)
- 残差结构
- 深度神经网络定义
- 单个神经元的计算
-
- Step1 累加求和
- Step2 激活
- 神经元在神经网络中的计算
- 反向传播算法内容
-
- Step1 计算误差
- Step2 更新权重
- 具体实例
-
- 实例简单理解
- 示例详解
-
- 下面是前向(前馈)运算
- 下面是反向传播
- 参数更新过程
- 误差E对w1的导数
- 卷积神经网络(Convolutional Neural Networks,CNN)
-
- 目录
- 参考链接
- 卷积运算
- 卷积背后的直觉
- 卷积神经网络的层级结构
-
- 输入层(Input layer)
- 卷积层(CONV layer)
-
- 卷积层的作用
- 神经元的空间排列
-
- 深度(depth)
- 步长(stride)
- 填充(padding)
- 几种不同卷积简介
-
- 扩张卷积 (Dilated Convolution)
- 分组卷积
- 深度可分离卷积
- 池化层(Pooling layer)
-
- 池化层作用
- 池化层分类
- 池化层特点
- 感受野
-
- 感受野介绍
- 感受野计算
- 计算实例
- 卷积神经网络中的不变性
- 非线性映射函数
-
- 激活函数作用
- 几种激活函数
-
- Sigmoid激活函数
- Tanh激活函数
- ReLU
- 激励层建议
- 优化器
- 通用矩阵乘(GEMM)
- Flatten层与全连接层(FC layer)
- 全连接与卷积转换
-
- 将卷积层转化成全连接层
- 将全连接层转化成卷积层
- 参数初始化
- 归一化
-
- 内部协变量偏移
- 几种归一化展示
- 批归一化
-
- 具体步骤
- 优缺点
- 层归一化
- 实例归一化
- 组归一化
- 自适应的归一化
- 正则化与Dropout
-
- 正则化
- Drpout
- Vanilla Dropout与Inverted Dropout
- Dropout 和 DropBlock
- 权重衰减(weight decay)
- 适用
- 卷积神经网络的训练
-
- 卷积网络示意图
- 单层卷积层
-
- 卷积的导数及反向传播
- 多通道
- 使⽤ GEMM 转换
- 单层池化层
-
- 池化的导数及后向传播
- 上采样
- 数据增强
-
- 翻转(Flip)
- 随机裁剪(crop采样)
- fancy PCA
- 样本不均衡
- 其余数据增强方式
- 训练和测试间的协调
- 超参数的调节
-
- 学习率(Learning Rate)
- batch_size选择
- 其余超参数
- 误差
- 卷积神经网络典型CNN
-
- 简介
- LeNet-5
-
- 结构与重要讨论
- LeNet-5全流程详解
- LeNet论文
- AlexNet
-
- AlexNet结构
- 局部响应归一化(Local response normalization,LRN)
- AlexNet创新点
- AlexNet全流程详解
- 训练细节
- AlexNet论文
- LeNet与AlexNet结构对比
- ZF Net
-
- ZF Net结构
- 反向操作介绍
-
- 反池化(上采样)
- 反(转置)卷积
- 可视化
- 平移-缩放-旋转
- 卷积核选择
- ZF Net与AlexNet
- 验证模型可感知具体位置
- 不同部位的相关性
- ZFNet论文
- 对比AlexNet与ZFNet
- VGGNet(Visual Geometry Group Net)
-
- VGGNet结构
- 几个重要的问题
- 3x3卷积核的作用(优势)
- 1 x 1卷积核作用
- VGGNet论文
- ZFNet与VGGnet
- HOOK
- GoogLeNet
-
- 问题综述
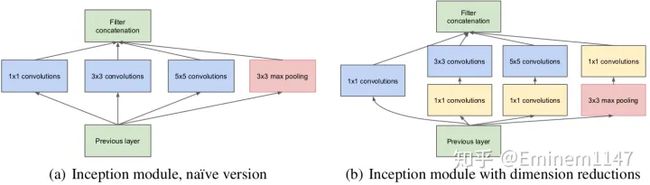
- Inception module
- 模型
- 优点
- 训练细节
- GoogLeNet V2
- GoogleNet V3
- GoogleNet V4
- GoogLenet论文
- VGGNet与GoogLeNet
- ResNet
-
- 问题综述
- 残差结构介绍
- bottleneck的残差结构
- ResNet结构
- 再读Batch Normalization
- 迁移学习0
- ResNet论文
- DenseNet
-
- 问题综述
- DenseBlock+Transition
- DenseNet特点
- SeNet
-
- 问题综述
- Squeeze+Excitation
- SE-Inception+SE-ResNet
- ResNet论文
- MobileNet
-
- MobileNet介绍
- 深度可分离卷积
- 计算量对比
- 两个超参数
- MobileNetV2
- MobileNetV3
- ShuffleNet
-
- ShuffleNetV1
- ShuffleNetV2
- RepVGG
-
- 问题综述
- 选择VGG网络的原因
- RepVGG主体结构
- 多分支融合技术
-
- 卷积层和BN层合并
- 3x3卷积和1x1卷积融合
- identity分支等效特殊权重
- 融合最终结构
- 深层卷积
- MobileOne
-
- 问题综述
- 过参数化
- building block
- 训练优化技巧
- FasterNet
-
- 问题综述
- 部分卷积
- FasterNet网络
- 学习复现重点
- 区域卷积神经网络(Regions with CNN features,R-CNN)
-
- 目标检测简介
-
- 传统目标检测
- DPM
- 选择性搜索(Selective Search)
- 分层合并
- 交并比(Intersection over Union,IOU)
- mAP
- RCNN_NMS
- R-CNN
-
- 简介
- 回归微调(fine-tuning)
- 训练过程
- 训练建议
- 全流程
- SPP Net
-
- 简介
- 映射
- 空间金字塔
- SPPNet训练
- 训练建议
- 全流程
- Fast R-CNN
-
- 简介
- Fast R-CNN引入三种新技术
-
- RoI Pooling Layer
- 多任务损失函数(Multi-task loss)
- SVD
- 预训练
- 几个问题
- 全流程
- 训练建议
- 相对于SPPNet
- Faster R-CNN
-
- 简介
- RPN
- Anchor(锚点)
- ROL池化
- 正负样例
- 损失定义
- 全流程
- R-CNN、SPP Net、Fast R-CNN、Faster R-CNN
- R-FCN
-
- 全连接带来的问题
- ResNet中加入ROI层讨论
- 网络结构
- 全流程
- SSD
-
- 简介
- 亮点
-
- 重用Faster R-CNN的Anchors机制(Default boxes and aspect ratios)
- 多尺度特征图抽样(Multi-scale feature maps for detection)
- 全卷积网络结构(Convolutional predictors for detection)
- 结构
- 膨胀卷积
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
神经网络的反向传播原理
神经网络之反向传播算法(BP)公式推导(超详细) - jsfantasy - 博客园 (cnblogs.com)
(50条消息) “反向传播算法”过程及公式推导(超直观好懂的Backpropagation)_aift的博客-CSDN博客
几个重要问题
深度学习和神经网络的关系
先来梳理一下什么是机器学习,什么是深度学习,而什么又是神经网络
其实在深度学习火之前,机器学习各种算法为人工智能的核心工具,其中就包括神经网络,然而在深度学习的空前发展影响下,现在机器学习中最为受欢迎的算法则从传统的SVM算法变为当今的神经网络,但是这里说的神经网络指代的是深层神经网络,即深度学习的基本理念
通俗地讲,机器学习为实现人工智能的途径,而神经网络隶属于机器学习中一种具体的算法方向,其中深度学习即深层神经网络为神经网络中的一种,因此我们可以简单理解为:深度学习==深层神经网络、深度学习 ∈ 机器学习, 如下图所示:
什么是神经网络
我们常常使用深度学习这个术语来指代神经网络训练的过程,特别是大规模的训练,那么神经网络到底是什么呢?
1.简单的房价预测网络
线性回归,我们将其看做一个神经元(neuron)比较合适,我们将为我们的房屋面积作为输入(我们称之为x)传入神经网络,通过一个函数或者说神经元,最终输出了价格(我们用y表示),在深度学习中,神经元的概念与线性函数的概念是等价的,通俗来讲,神经元其实没听着那么高大上,其本质就为线性函数 : y = a ∗ x + b y=a*x+b y=a∗x+b
然而上例中我们可以看到,线性函数 y = a ∗ x + b y=a*x+b y=a∗x+b满足不了非线性的拟合,因为价格不可能存在负数,因此我们必须需要非线性元素来表达,其中例子中采取的截断手段(将y小于0的区域置为0)在深度学习中是一个非常受欢迎的非线性激活函数,称为修正线性函数(Rectified Linear Unit),又称为Relu激活函数,其函数表达式为 : m a x ( 0 , x ) max(0,x) max(0,x),当今几乎所有的神经网络都会用到Relu激活函数来表达模型中的非线性元素
2.两层的房价预测网络
搭建好网络,设定好学习规则(稍后会详细说明),开启循环训练,在将特征输入模型,得到预测的结果
因此我们现在回头来看一下神经网络,其就是由多层网络构成,其中每一层网络中都包含n个节点或神经元,每个神经元的本质原理无非是线性函数+激活函数(Relu,Sigmoid等),在构建好网络之后,设定模型学习的规则,然后把数据丢进去,它就会开始自己在数据中学习特征之间的联系了,是不是觉得很神奇呢哈哈哈,上面我们所了解的只是神经网络中的一点皮毛而已啦,具体的学习规则等都还没开始介绍,稍后我们开始讨论神经网络到底是怎么学习的.
神经网络如何进行学习
向量化操作
向量化计算 w T x w^{T}x wTx的方法,我们将会发现向量化后的计算速度将会提升百倍级,大大减少了我们的代码量与计算时间,是一个非常好用的深度学习技巧
在深度学习中,单层神经元数量往往是大于1的,因此单纯向量化w还不足满足要求,因此在深度学习中,一般w所代表的是为矩阵而不是向量,其中我们称w为权重矩阵,权重矩阵行数所代表的为神经元个数,权重矩阵列数代表的为输入特征数

3代表神经元个数,4代表每个神经元输入特征个数
损失函数
损失函数(Loss Function)又称为代价函数(Cost Function)
损失函数来衡量我们的输出值和实际值(标签)有多接近,换句话说,损失函数是用来评估我们模型的好坏的,损失函数越小,模型效果越拟合对应的精准函数
交叉熵损失函数(Cross Entropy Error Function)
J ( w , b ) = − 1 m ∑ a b L ( y ~ ( i ) , y ( i ) ) = 1 m ∑ i = 1 m ( − y ( i ) l o g y ˉ ( i ) − ( 1 − y ( i ) ) l o g ( 1 − y ~ ( i ) ) ) J(w,b)=-\frac{1}{m}\sum_{a}^{b}L\left(\tilde{y}^{(i)},y^{(i)}\right)=\frac{1}{m}\sum_{i=1}^{m}(-y^{(i)}log\bar{y}^{(i)}-(1-y^{(i)})log(1-\tilde{y}^{(i)})) J(w,b)=−m1a∑bL(y~(i),y(i))=m1i=1∑m(−y(i)logyˉ(i)−(1−y(i))log(1−y~(i)))
其中 y ( i ) y^{(i)} y(i)表示为i样本的标签(在图像分类中,样本标签通常为one-hot格式),样本标签具体可解释为指明当前样本所需哪一类对象,如现在我们有一个图像分类,每一张图像样本都会对应一个标签,如现在我们有一个分类任务 [ c a t , c a r , f r o g ] [cat,car,frog] [cat,car,frog],如图 2-6所示,其中所有猫cat的图像样本(最左)对应的标签格式为 [1,0,0] ,所有图像样本(中间)对应的标签格式为 [0,1,0] ,这就是所谓的图像分类one-hot标签格式,也是最常用的一种标签格式
现在我们将交叉熵损失函数中i定为2,将多分类问题简化为二分类问题,公式变形如下:
L ( y ~ , y ) = − y l o g ( y ~ ) − ( 1 − y ) l o g ( 1 − y ~ ) L(\tilde{y},y)=-ylog(\tilde{y})-(1-y)log(1-\tilde{y}) L(y~,y)=−ylog(y~)−(1−y)log(1−y~)
- 因此当 y = 1 时损失函数 L = -log(g),如果想要损 L尽可能小,那么 就要尽可能大,而又因为sigmoid函数取值 0,1 ,所以 会无限接近于1
- 当 y =0 时损失函数 L = -log(1 -),如果想要损 L尽可能小那么 就要尽可能小,而又因为sigmoid函数取值 0,1,所以会无限接近于0
所以我们可以小结一下,损失函数是评价模型的一个指标,整个神经网络训练的目的即尽可能降低损失函数,使其变为拟合训练数据较优模型,为实际训练中理想的损失函数变换曲线
学习率退火(learning rate annealing)
学习率在神经网络训练过程也是一个非常重要的超参数,之前我们提到了训练过程就是寻找最优解的过程,但是假如我们一次更新过大或者说步长过大,将会出现在最优解点位附近来回跳跃的情况
因此我们要让学习率随着时间的慢慢的变小,才能让模型一开始节省大量时间,后期为确保精度而使用较小的学习率,通常实现学习率退火有3种方式
- 随步数衰减:每进行几个周期就根据一些因素降低学习率。典型的值是每过5个周期就将学习率减少一半,或者每20个周期减少到之前的0.1。这些数值的设定是严重依赖具体问题和模型的选择的。在实践中可能看见这么一种经验做法:使用一个固定的学习率来进行训练的同时观察验证集错误率,每当验证集错误率停止下降,就乘以一个常数(比如0.5)来降低学习率
- 指数衰减:数学公式是 α = α 0 e − k t \alpha=\alpha_{0}e^{-kt} α=α0e−kt,其中 α 0 , k \alpha_{0},k α0,k是超参数,,t是迭代次数(也可以使用周期作为单位)
- 1/t衰减:数学公式是 α = α 0 / ( 1 + k t ) \alpha=\alpha_{0}/(1+kt) α=α0/(1+kt),其中 α 0 , k \alpha_{0},k α0,k是超参数,t是迭代次数
为什么神经网络用到梯度下降优化方法
深度网络是由许多非线性层(带有激活函数)堆叠而成,每一层非线性层可以视为一个非线性函数f(x),因此整个深度网络可以视为一个复合的非线性多元函数:
F ( x ) = f n ( … f 3 ( f 2 ( f 1 ( x ) × θ 1 + b ) × θ 2 + b ) … ) F(x)=f_n(\ldots f_3(f_2(f_1(x)\times\theta_1+b)\times\theta_2+b)\ldots) F(x)=fn(…f3(f2(f1(x)×θ1+b)×θ2+b)…)
我们的目的是希望这个多元函数可以很好的完成输入到输出的映射,假设不同的输入,输出最优解是 g(x),那么优化深度网络就是为了寻找到合适的权值,满足 Loss = L(g(t),F(t) 取得最小值点,比如简单的损失函数平方差:
L o s s = ∣ ∣ g ( x ) − f ( x ) ∣ ∣ 2 2 Loss=||g(x)-f(x)||_2^2 Loss=∣∣g(x)−f(x)∣∣22
在数学中寻找最小值问题,采用梯度下降的方法再合适不过了
梯度消失和梯度爆炸
梯度消失和梯度爆炸
梯度消失和梯度爆炸两种情况产生的原因可以总结成2类原因:1.深层网络的结构;2.**不合适的激活函数,**比如Sigmoid函数。梯度爆炸一般出现在深层网络和权值初始化值太大的情况下
- 深层网络的结构
反向传播算法基于梯度下降的思想,以目标负梯度方向对参数进行调整,参数的更新为 w = w − α ∂ L o s s ∂ w w=w-\alpha\frac{\partial Loss}{\partial w} w=w−α∂w∂Loss,如果要更新第二隐藏层的权值信息,根据链式求导:
Δ w 2 = ∂ L o s s ∂ w 2 = ∂ L o s s ∂ f 4 ∂ f 4 ∂ f 3 ∂ f 3 ∂ f 2 ∂ f 2 ∂ w 2 \Delta w_2=\frac{\partial Loss}{\partial w_2}=\frac{\partial Loss}{\partial f_4}\frac{\partial f_4}{\partial f_3}\frac{\partial f_3}{\partial f_2}\frac{\partial f_2}{\partial w_2} Δw2=∂w2∂Loss=∂f4∂Loss∂f3∂f4∂f2∂f3∂w2∂f2
其实类似 ∂ f 4 ∂ f 3 \frac{\partial f_{4}}{\partial f_{3}} ∂f3∂f4就是对激活函数进行求导。如果在此部分大于1,那么随着层数的增加,求出的梯度的更新将以指数形式增加,发生梯度爆炸。如果此部分小于1,那么随着层数的增加求出的梯度更新的信息会以指数形式衰减,发生梯度消失
从深层网络角度来说,不同的层学习的速度差异很大,表现为网络中靠近输出的层学习的情况很好,靠近输入层的学习很慢,甚至即使训练了很久,前基层的权值和刚开始初始化的值差不多,因此梯度消失和梯度爆炸的根本原因在于反向传播算法的不足
2.不合适的激活函数
如果激活函数的选择不合适,比如使用Sigmoid,梯度消失会很明显
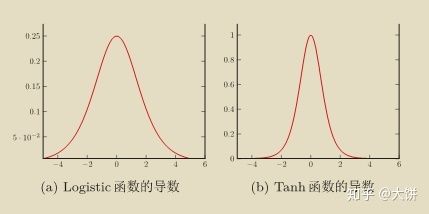
下图为Logistic函数和Tanh函数的导数,Logistic导数最大的时候也只有0.25,其余时候远小于0.25,因此如果每层的激活函数都为Logistic函数的话,很容易导致梯度消失问题,Tanh函数的导数峰值是1那也仅仅在取值为0的时候,其余时候都是小于1,因此通过链式求导之后,Tanh函数也很容易导致梯度消失
梯度消失、爆炸的解决方案
预训练和微调
预训练:无监督逐层训练,每次训练一层隐藏点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入。称为逐层预训练。在预训练完成后还要对整个网络进行微调
梯度剪切、正则
梯度剪切又叫梯度截断,是防止梯度爆炸的一种方法,其思想是设置一个梯度剪切阈值,更新梯度的时候,如果梯度超过这个阈值,那就将其强制限制在这个范围之内
梯度截断的方式有2种:
- 按值截断: 在第t次选代时,梯度为 gt ,给定一个区间[a,b],如果一个参数的梯度小于a时,就将其设为a;如果大于b时,就将其设为b
- 按模截断: 将梯度的模截断到一个给定的截断值b。如果 ∣ ∣ g t ∣ ∣ 2 ≤ b ||g_{t}||^{2}\leq b ∣∣gt∣∣2≤b,保持 g t g_t gt不变。如果 ∣ ∣ g t ∣ ∣ 2 > b , ∣ ∣ g t ∣ ∣ = b ∣ ∣ g t ∣ ∣ g t ||g_t||^2>b,||g_t||=\frac b{||g_t||}g_t ∣∣gt∣∣2>b,∣∣gt∣∣=∣∣gt∣∣bgt,b为超参数,往往一个小的闻值可以达到很好的效果。在训练循环神经网络时,按模截断是避免题都爆炸问题的有效方法
- 另一种解决梯度爆炸的手段是采用权重正则化,较常见的是l1正则和l2正则,正则化是通过对网络权重做正则限制过拟合,仔细看正则项在损失函数的形式: L o s s = ( y − W T x ) 2 + λ ∣ ∣ W ∣ ∣ 2 Loss=(y-W^Tx)^2+\lambda||W||^2 Loss=(y−WTx)2+λ∣∣W∣∣2, λ \lambda λ是正则项系数,如果发生梯度爆炸,权值的范数会变得非常大,通过正则化项,可以部分限制梯度爆炸的发生
relu、leakyrelu、elu等激活函数
从relu的函数特性我们知道,在小于0的时候梯度为0,大于0的时候梯度恒为1,那么此时就不会再存在梯度消失和梯度爆炸的问题了,因为每层的网络得到的梯度更新速度都一样
relu的主要贡献:
- 解决了梯度消失和梯度爆炸的问题
- 计算方便计算速度快(梯度恒定为0或1)
- 加速了网络的训练
缺陷:
- 由于负数部分恒为0,导致一些神经元无法激活(可通过设置小学习率部分解决)
- 输出并不是零中心化的
关于激活函数在CNN章节会做详细介绍
Batch Normalization(批规范化)
正向传播中 f 2 = f 1 ( w T × x + b ) \ f_{2}=f_{1}(w^{T}\times x+b) f2=f1(wT×x+b),那么反向过程中, ∂ f 2 ∂ x = ∂ f 2 ∂ f 1 w \frac{\partial f_{2}}{\partial x}=\frac{\partial f_{2}}{\partial f_{1}}w ∂x∂f2=∂f1∂f2w,那么反向传播过程中w的大小影响了梯度消失和爆炸,BN就是通过对每一层的输出规范为均值和方差一致的方法,消除了w带来的放大缩小的影响,进而解决梯度消失和爆炸的问题,或者可以理解为BN将输出从饱和区拉到了非饱和区(比如Sigmoid函数)
残差结构

相比较以往的网络结构只是简单的堆叠,残差中有很多跨层连接结构,这样的结构在反向传播时具有很大的好处:
∂ L o s s ∂ x 1 = ∂ L o s s ∂ x L × ∂ x L ∂ x 1 = ∂ l o s s ∂ x L × ( 1 + ∂ ∂ x L ∑ i = 1 L − 1 F ( x i , W i ) ) \frac{\partial Loss}{\partial x_1}=\frac{\partial Loss}{\partial x_L}\times\frac{\partial x_L}{\partial x_1}=\frac{\partial loss}{\partial x_L}\times(1+\frac{\partial}{\partial x_L}\sum_{i=1}^{L-1}F(x_i,W_i)) ∂x1∂Loss=∂xL∂Loss×∂x1∂xL=∂xL∂loss×(1+∂xL∂i=1∑L−1F(xi,Wi))
∂ L o s s ∂ x L \frac{\partial Loss}{\partial x_L} ∂xL∂Loss表示损失函数到达L的梯度,小括号里的1表示**短路机制(identity x)**可以无损地传播梯度,而另一项残差梯度则需要经过带有weights的层,残差梯度不会那么巧全为-1,就算其很小,由于1的存在不会导致梯度消失,所以残差学习会更容易
深度神经网络定义
深度神经网络(Deep Neural Networks,DNN)或多层感知机(multilayer perceptron)或前馈神经网络(feedforward neural network)
三层神经网络来举例,如下:

神经网络由一层一层的神经元构成(1纵列称为这个神经网络的一层),因此在学习神经网络的前向传播时,应该先知道每个神经元是如何计算的
神经网络相比于传统方法具备:
- 并行
- 容错
- 硬件实现
- 自我学习
单个神经元的计算
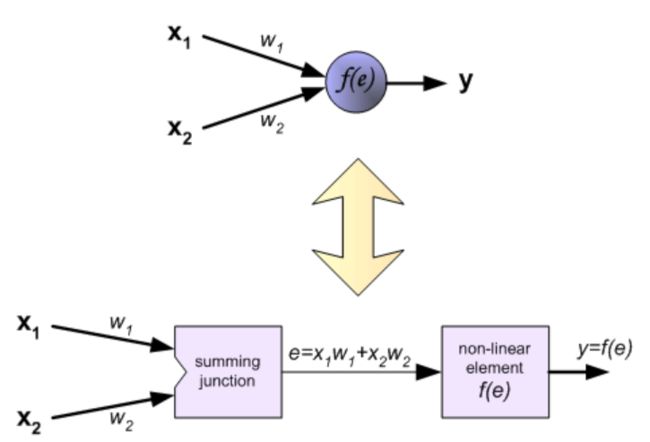
图中符号意义如下所示:
- 输入数据: x1,x2
- 权重参数: w1,w2
- 激活函数: f(e)输出: y
Step1 累加求和
输入数据和其对应的权重相乘并求和
e = x 1 w 1 + x 2 w 2 \mathrm{e}=\mathrm{x}_1\mathrm{~w}_1+\mathrm{x}_2\mathrm{~w}_2 e=x1 w1+x2 w2
Step2 激活
将第一步的输出通过一个非线性的激活函数激活(图中f(e)),得到输出y:y = f ( e )
神经元在神经网络中的计算
在全连接神经网络中,每一层的每个神经元都会与前一层的所有神经元或者输入数据相连,例如图中的f1(e)就与x1和x2分别相连。因此,在计算的时候,每一个神经元的输出=使用激活函数激活前一层函数的累加和,例如第一幅图中的f1(e)的输出y1, y 1 = f 1 ( w ( x 1 ) x 1 + w ( x 2 ) x 2 ) \mathrm{y}1=\mathrm{f}_1\left(\mathrm{w}_(\mathrm{x}1)\mathrm{x}_1\right.+\mathrm{w}_(\mathrm{x}2)\mathrm{x}_2\left.\right) y1=f1(w(x1)x1+w(x2)x2),下面的两个神经元的计算同理
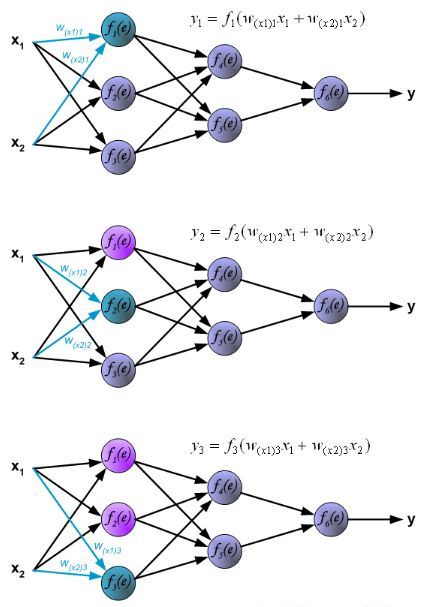
下图展示了第二层隐藏层的中神经元输出的计算方式
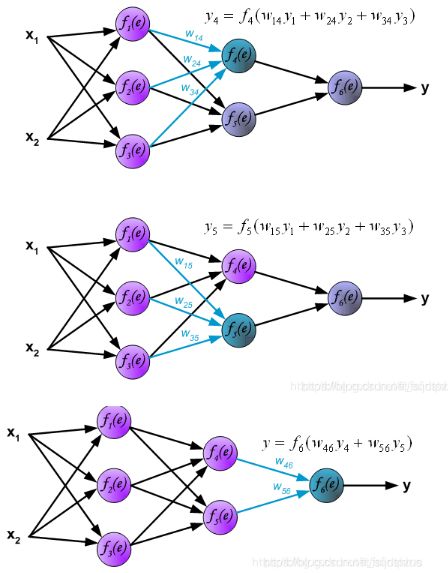
反向传播算法内容
反向传播(英语:Backpropagation,缩写为BP)是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。(误差的反向传播)
BP算法的学习过程由正向传播过程和反向传播过程组成
- 在正向传播过程中,输入信息通过输入层经隐含层,逐层处理并传向输出层。如果预测值和标签值不一样,则取输出与期望的误差的平方和作为损失函数(损失函数有很多,这是其中一种)
- 将正向传播中的损失函数传入反向传播过程,逐层求出损失函数对各神经元权重的偏导数,作为目标函数对权重的梯度。根据这个计算出来的梯度来修改权重,网络的学习在权重修改过程中完成。误差达到期望值时,网络学习结束
神经网络的反向传播可以分为2个步骤:
Step1 计算误差
第一步是计算神经网络的输出(预测值)和真值的误差
图中y为我们神经网络的预测值,由于这个预测值不一定正确,所以我们需要将神经网络的预测值和对应数据的标签来比较,计算出误差。误差的计算有很多方法,比如上面提到的输出与期望的误差的平方和,熵(Entropy)以及交叉熵等。计算出的误差记为 δ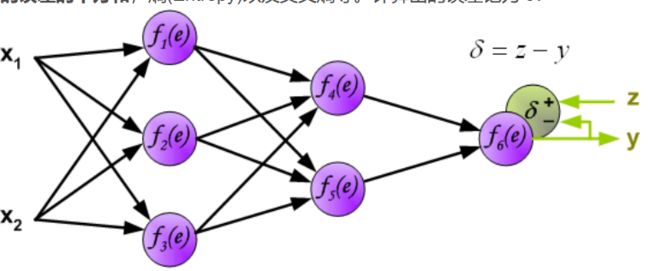
反向传播,是从后向前传播的一种方法。因此计算完误差后,需要将这个误差向不断的向前一层传播。向前一层传播时,需要考虑到前一个神经元的权重系数(因为不同神经元的重要性不同,因此回传时需要考虑权重系数)
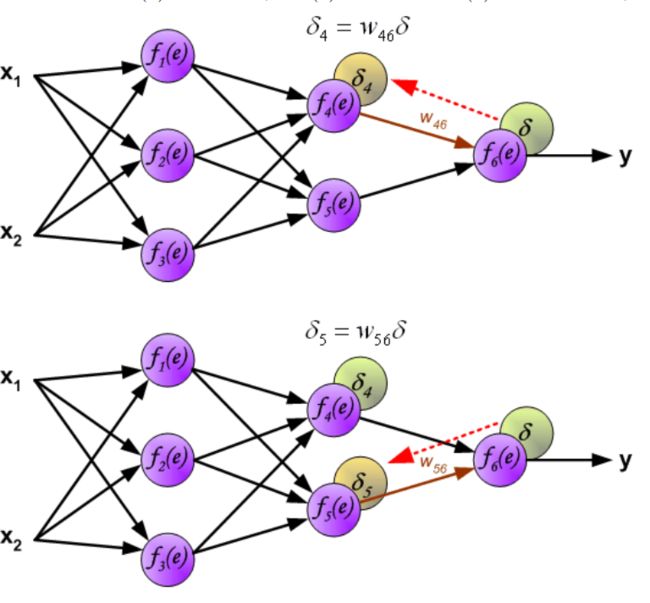
与前向传播时相同,反向传播时后一层的节点会与前一层的多个节点相连,因此需要对所有节点的误差求和+
Step2 更新权重
图中的η代表学习率,w ′ 是更新后的权重,通过这个式子来更新权重

具体实例
实例简单理解
首先明确,“正向传播”求损失,“反向传播”回传误差。同时,神经网络每层的每个神经元都可以根据误差信号修正每层的权重,只要能明确上面两点,那么下面的例子,只要会一点链式求导规则,就一定能看懂!BP算法,也叫δ 算法,下面以3层的感知机为例进行举例讲解
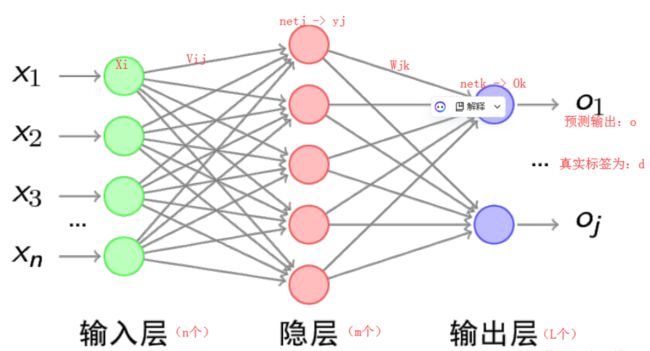
输出层:
E = 1 2 ( d − O ) 2 = 1 2 ∑ κ = 1 ℓ ( d k − o k ) 2 E=\frac{1}{2}(d-O)^2\quad=\frac{1}{2}\sum_{\kappa=1}^{\ell}(d_k-o_k)^2 E=21(d−O)2=21κ=1∑ℓ(dk−ok)2
误差展开至隐层:
E = 1 2 ∑ κ = 1 ℓ [ d κ − f ( n e t κ ) ] 2 = 1 2 ∑ κ = 1 ℓ [ d κ − f ( ∑ j = 0 m ω j κ y j ) ] 2 E=\frac12\sum_{\kappa=1}^{\ell}[d_{\kappa}-f(net_{\kappa})]^{2}\quad=\frac12\sum_{\kappa=1}^{\ell}[d_{\kappa}-f(\sum_{j=0}^{m}\omega_{j\kappa}y_{j})]^{2} E=21κ=1∑ℓ[dκ−f(netκ)]2=21κ=1∑ℓ[dκ−f(j=0∑mωjκyj)]2
展开至输入层:
E = 1 2 ∑ κ = 1 ℓ d κ − f [ ∑ j = 0 m ω j κ f ( n e t j ) ] 2 = 1 2 ∑ κ = 1 ℓ d κ − f [ ∑ j = 0 m ω j κ f ( ∑ z ˙ = 0 n v i j ℓ i ) ] 2 E=\frac{1}{2}\sum_{\kappa=1}^{\ell}d_{\kappa}-f[\sum_{j=0}^{m}\omega_{j\kappa}f(net_{j})]^{2}\quad=\frac{1}{2}\sum_{\kappa=1}^{\ell}d_{\kappa}-f[\sum_{j=0}^{m}\omega_{j\kappa}f(\sum_{\dot{z}=0}^{n}v_{ij\ell i})]^{2} E=21κ=1∑ℓdκ−f[j=0∑mωjκf(netj)]2=21κ=1∑ℓdκ−f[j=0∑mωjκf(z˙=0∑nvijℓi)]2现在还有两个问题需要解决:
- 误差E有了,怎么调整权重让误差不断减小?
- E是权重w的函数,何如找到使得函数值最小的w
解决上面问题的方法是梯度下降算法

示例详解
下面是前向(前馈)运算
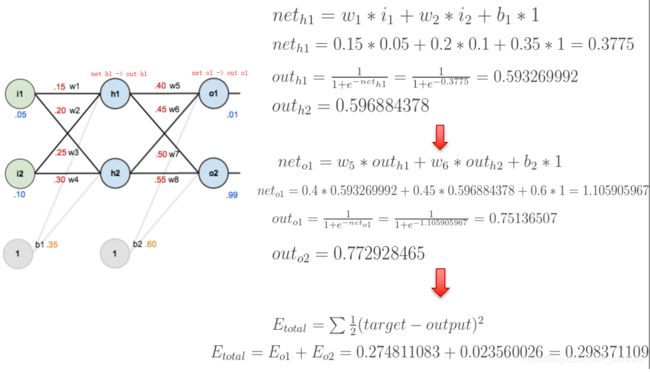
激活函数为sigmoid
下面是反向传播
求网络误差对各个权重参数的梯度
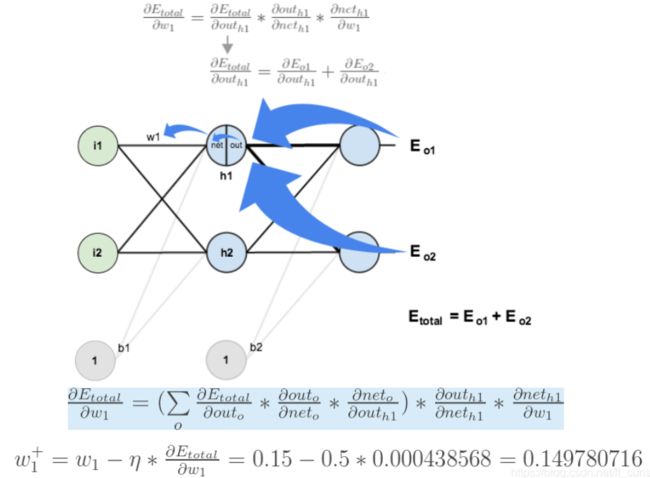
参数更新过程
误差E对w1的导数
卷积神经网络(Convolutional Neural Networks,CNN)
目录
文章目录
- 前言
-
- Stacking(堆叠)
- 深度学习/神经网络
- **深度神经网络**(Deep Neural Networks,DNN)
-
- 几个重要问题
-
- 深度学习和神经网络的关系
- 什么是神经网络
- 神经网络如何进行学习
-
- 向量化操作
- 损失函数
- 学习率退火(learning rate annealing)
- 为什么神经网络用到梯度下降优化方法
- 梯度消失和梯度爆炸
-
- 梯度消失和梯度爆炸
- 梯度消失、爆炸的解决方案
-
- 预训练和微调
- 梯度剪切、正则
- relu、leakyrelu、elu等激活函数
- Batch Normalization(批规范化)
- 残差结构
- 深度神经网络定义
- 单个神经元的计算
-
- Step1 累加求和
- Step2 激活
- 神经元在神经网络中的计算
- 反向传播算法内容
-
- Step1 计算误差
- Step2 更新权重
- 具体实例
-
- 实例简单理解
- 示例详解
-
- 下面是前向(前馈)运算
- 下面是反向传播
- 参数更新过程
- 误差E对w1的导数
- 卷积神经网络(Convolutional Neural Networks,CNN)
-
- 目录
- 参考链接
- 卷积运算
- 卷积背后的直觉
- 卷积神经网络的层级结构
-
- 输入层(Input layer)
- 卷积层(CONV layer)
-
- 卷积层的作用
- 神经元的空间排列
-
- 深度(depth)
- 步长(stride)
- 填充(padding)
- 几种不同卷积简介
-
- 扩张卷积 (Dilated Convolution)
- 分组卷积
- 深度可分离卷积
- 池化层(Pooling layer)
-
- 池化层作用
- 池化层分类
- 池化层特点
- 感受野
-
- 感受野介绍
- 感受野计算
- 计算实例
- 卷积神经网络中的不变性
- 非线性映射函数
-
- 激活函数作用
- 几种激活函数
-
- Sigmoid激活函数
- Tanh激活函数
- ReLU
- 激励层建议
- 优化器
- 通用矩阵乘(GEMM)
- Flatten层与全连接层(FC layer)
- 全连接与卷积转换
-
- 将卷积层转化成全连接层
- 将全连接层转化成卷积层
- 参数初始化
- 归一化
-
- 内部协变量偏移
- 几种归一化展示
- 批归一化
-
- 具体步骤
- 优缺点
- 层归一化
- 实例归一化
- 组归一化
- 自适应的归一化
- 正则化与Dropout
-
- 正则化
- Drpout
- Vanilla Dropout与Inverted Dropout
- Dropout 和 DropBlock
- 权重衰减(weight decay)
- 适用
- 卷积神经网络的训练
-
- 卷积网络示意图
- 单层卷积层
-
- 卷积的导数及反向传播
- 多通道
- 使⽤ GEMM 转换
- 单层池化层
-
- 池化的导数及后向传播
- 上采样
- 数据增强
-
- 翻转(Flip)
- 随机裁剪(crop采样)
- fancy PCA
- 样本不均衡
- 其余数据增强方式
- 训练和测试间的协调
- 超参数的调节
-
- 学习率(Learning Rate)
- batch_size选择
- 其余超参数
- 误差
- 卷积神经网络典型CNN
-
- 简介
- LeNet-5
-
- 结构与重要讨论
- LeNet-5全流程详解
- LeNet论文
- AlexNet
-
- AlexNet结构
- 局部响应归一化(Local response normalization,LRN)
- AlexNet创新点
- AlexNet全流程详解
- 训练细节
- AlexNet论文
- LeNet与AlexNet结构对比
- ZF Net
-
- ZF Net结构
- 反向操作介绍
-
- 反池化(上采样)
- 反(转置)卷积
- 可视化
- 平移-缩放-旋转
- 卷积核选择
- ZF Net与AlexNet
- 验证模型可感知具体位置
- 不同部位的相关性
- ZFNet论文
- 对比AlexNet与ZFNet
- VGGNet(Visual Geometry Group Net)
-
- VGGNet结构
- 几个重要的问题
- 3x3卷积核的作用(优势)
- 1 x 1卷积核作用
- VGGNet论文
- ZFNet与VGGnet
- HOOK
- GoogLeNet
-
- 问题综述
- Inception module
- 模型
- 优点
- 训练细节
- GoogLeNet V2
- GoogleNet V3
- GoogleNet V4
- GoogLenet论文
- VGGNet与GoogLeNet
- ResNet
-
- 问题综述
- 残差结构介绍
- bottleneck的残差结构
- ResNet结构
- 再读Batch Normalization
- 迁移学习0
- ResNet论文
- DenseNet
-
- 问题综述
- DenseBlock+Transition
- DenseNet特点
- SeNet
-
- 问题综述
- Squeeze+Excitation
- SE-Inception+SE-ResNet
- ResNet论文
- MobileNet
-
- MobileNet介绍
- 深度可分离卷积
- 计算量对比
- 两个超参数
- MobileNetV2
- MobileNetV3
- ShuffleNet
-
- ShuffleNetV1
- ShuffleNetV2
- RepVGG
-
- 问题综述
- 选择VGG网络的原因
- RepVGG主体结构
- 多分支融合技术
-
- 卷积层和BN层合并
- 3x3卷积和1x1卷积融合
- identity分支等效特殊权重
- 融合最终结构
- 深层卷积
- MobileOne
-
- 问题综述
- 过参数化
- building block
- 训练优化技巧
- FasterNet
-
- 问题综述
- 部分卷积
- FasterNet网络
- 学习复现重点
- 区域卷积神经网络(Regions with CNN features,R-CNN)
-
- 目标检测简介
-
- 传统目标检测
- DPM
- 选择性搜索(Selective Search)
- 分层合并
- 交并比(Intersection over Union,IOU)
- mAP
- RCNN_NMS
- R-CNN
-
- 简介
- 回归微调(fine-tuning)
- 训练过程
- 训练建议
- 全流程
- SPP Net
-
- 简介
- 映射
- 空间金字塔
- SPPNet训练
- 训练建议
- 全流程
- Fast R-CNN
-
- 简介
- Fast R-CNN引入三种新技术
-
- RoI Pooling Layer
- 多任务损失函数(Multi-task loss)
- SVD
- 预训练
- 几个问题
- 全流程
- 训练建议
- 相对于SPPNet
- Faster R-CNN
-
- 简介
- RPN
- Anchor(锚点)
- ROL池化
- 正负样例
- 损失定义
- 全流程
- R-CNN、SPP Net、Fast R-CNN、Faster R-CNN
- R-FCN
-
- 全连接带来的问题
- ResNet中加入ROI层讨论
- 网络结构
- 全流程
- SSD
-
- 简介
- 亮点
-
- 重用Faster R-CNN的Anchors机制(Default boxes and aspect ratios)
- 多尺度特征图抽样(Multi-scale feature maps for detection)
- 全卷积网络结构(Convolutional predictors for detection)
- 结构
- 膨胀卷积
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
参考链接
一文入门卷积神经网络:CNN通俗解析 - 知乎 (zhihu.com)
卷积神经网络(CNN)详解 (zhihu.com)
深度学习入门-卷积神经网络(一)卷积层 - 知乎 (zhihu.com)
11张图带你入门深度学习卷积层工作原理 - 知乎 (zhihu.com)
一文让你理解什么是卷积神经网络 - 简书 (jianshu.com)
机器学习算法之——卷积神经网络(CNN)原理讲解_神经网络_迈微AI研发社_InfoQ写作社区
大白话讲解卷积神经网络工作原理 - 知乎 (zhihu.com)
卷积神经网络(CNN)基础及经典模型介绍 - 知乎 (zhihu.com)
深度学习之17——归一化(BN+LN+IN+GN) - 知乎 (zhihu.com)
(53条消息) 图解——深度学习中数据归一化(BN,LN,IN,SN)_深度图归一化_Mr DaYang的博客-CSDN博客
深度学习之9——逐层归一化(BN,LN) - 知乎 (zhihu.com)
【深度学习理论】一文搞透Dropout、L1L2正则化/权重衰减 - 知乎 (zhihu.com)
数据增强(Data Augmentation) - 知乎 (zhihu.com)
(53条消息) 数据增强的方法总结及代码实现_数据增强代码_搞视觉的张小凡的博客-CSDN博客
一文看尽深度学习中的各种数据增强 - 知乎 (zhihu.com)
深度学习中的超参数调节(learning rate、epochs、batch-size…) - 知乎 (zhihu.com)
深度学习中Epoch、Batch以及Batch size的设定 - 知乎 (zhihu.com)
经典论文之LeNet - 知乎 (zhihu.com)
CV论文精读系列之分类模型(一):AlexNet - 知乎 (zhihu.com)
CNN基础论文 精读+复现----ZFnet(一)_深度不学习的技术博客_51CTO博客
(53条消息) 详解深度学习之经典网络架构(三):ZFNet_chenyuping666的博客-CSDN博客
温故知新!一战成名的AlexNet的6个关键点总结 - 知乎 (zhihu.com)
【论文精读3】VGGNet——《Very Deep Convolutional Networks for Large-Scale Image Recognition》 - 知乎 (zhihu.com)
(53条消息) 深度学习基础学习-1x1卷积核的作用(CNN中)_1*1卷积核的作用_小夭。的博客-CSDN博客
(53条消息) 感受野详解_CtrlZ1的博客-CSDN博客
vggnet代码复现:
- 使用pytorch,搭建VGGNet神经网络结构(附代码) - 掘金 (juejin.cn)
- (52条消息) 使用pytorch实现VGG16模型(小白学习,详细注释)_vgg16 pytorch_一个小猴子`的博客-CSDN博客
- 如何用PyTorch构建一个VGG16网络?(附代码) - 知乎 (zhihu.com)
深度学习经典论文分析(七)-Going deeper with convolutions - 知乎 (zhihu.com)
Inception-v1 论文详解 - 知乎 (zhihu.com)
ResNet论文笔记及代码剖析 - 知乎 (zhihu.com)
一文读懂残差网络ResNet - 知乎 (zhihu.com)
DenseNet:比ResNet更优的CNN模型 - 知乎 (zhihu.com)
深入解析DenseNet(含大量可视化及计算) - 知乎 (zhihu.com)
卷积神经网络学习笔记——SENet - 知乎 (zhihu.com)
卷积神经网络学习笔记——SENet - 知乎 (zhihu.com)
注意力机制之Residual Attetion Network - 知乎 (zhihu.com)
Residual Attention Network论文笔记 - 知乎 (zhihu.com)
MobilenetV1论文阅读 - 知乎 (zhihu.com)
CNN模型之ShuffleNet - 知乎 (zhihu.com)
深度解读:RepVGG - 知乎 (zhihu.com)
图解RepVGG - 知乎 (zhihu.com)
RepVGG论文详解以及使用Pytorch进行模型复现 - 知乎 (zhihu.com)
比ResNet更强的RepVGG代码详解_潮生灬的博客-CSDN博客
全网唯一复现!手机端 1ms 级延迟的主干网模型 MobileOne - 知乎 (zhihu.com)
深度学习理论与实践—MobileOne:Apple基于重参数化的手机端主干网络 - 知乎 (zhihu.com)
(54条消息) MobileOne实战:使用MobileOne实现图像分类任务(一)_AI浩的博客-CSDN博客
【CVPR2023】FasterNet:追逐更高FLOPS、更快的神经网络 - 飞桨AI Studio (baidu.com)
通用 Vision Backbone 超详细解读 (二十二):FasterNet:追求更快的神经网络 - 知乎 (zhihu.com)
卷积运算
跳转到参考链接
卷积操作是指对不同的数据窗口数据 (图像) ⽤一组固定的权重 (滤波矩阵,可以看做⼀个恒定的滤波器 Filter) 逐个元素相乘再求和 (做内积)
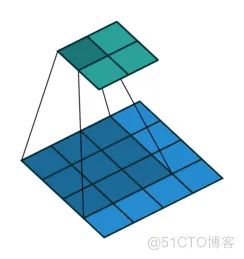
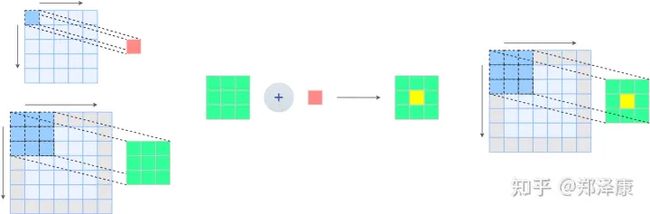
二维卷积运算:
我们通常在卷积层中会使⽤更加直观的互相关 (Cross-correlation) 运算。例如,在⼆维卷积层中,⼀个⼆维输⼊数组 I 和⼀个⼆维核数组 K 通过互相关运算输出⼀个⼆维数组 O。
如图所⽰,输⼊是⼀个⾼和宽均为 3 的⼆维数组,核数组 (也称卷积核或过滤器) 的⾼和宽分别为 2。因此,我们可以说输⼊数组形状为(3*,* 3),卷积核(又称卷积窗) 的形状为 (2*,* 2)
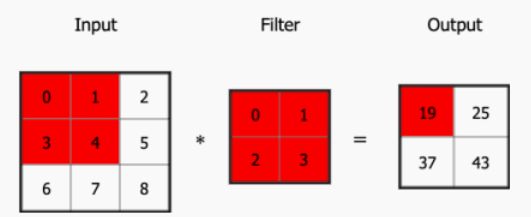
输⼊的红⾊区域与核的红⾊区域通过运算得到输出的左上⾓红⾊区域
卷积背后的直觉
我们将卷积操作⽅式展开成前馈⽹络的形式,如图所⽰,左图为原本的前馈⽹络,右图为卷积操作。在深度前馈⽹络中,权重矩阵中的每一个元素只会使用一次,不会在不同的输⼊位置上共享参数
⽽在卷积操作中,卷积核的每一个元素都作用在输入的每一位置上。这个设计保证了我们只需要学习⼀个参数集合,⽽不⽤对每⼀位置去学习⼀个单独的参数

这便是卷积的直觉,稀疏交互 (Sparse Interactions) 与参数共享 (Parameter Sharing)。前馈⽹络中每⼀个输出单元与每⼀个输⼊单元都产⽣交互,如果有 m 个输⼊和 n 个输出,那么矩阵乘法需要 m × n 个参数并且相应算法的时间复杂度为 O(m × n)
卷积操作中如果我们限制每⼀个输出拥有的连接数为 k,那么稀疏的连接⽅法只需要 k × n 个参数以及 O(k × n) 的运⾏时间
卷积神经网络的层级结构
跳转到参考链接
如果用全连接神经网络处理大尺寸图像具有三个明显的缺点:
- 首先将图像展开为向量会丢失空间信息
- 其次参数过多效率低下,训练困难
- 同时大量的参数也很快会导致网络过拟合
卷积神经网络一些特点:
- 局部感知: 在进行计算的时候,将图片划分为一个个的区域进行计算/考虑
- 权值共享机制:假设每个神经元连接数据窗的权重是固定的
- 滑动窗口重叠:降低窗口与窗口之间的边缘不平滑的特性
- 固定每个神经元的连接权重,可以将神经元看成一个模板(卷积核);也就是每个卷积核只关注一个特性
- 需要计算的权重个数会大大的减少
- **备注:**一组固定的权重和窗口内数据做矩阵内积后求和的过程叫做卷积
优点:
- 局部感知的共享卷积核(共享参数),对高维数据的处理没有压力
- 无需选择特征属性,只要训练好权重,即可得到特征值
- 深层次的网络抽取图像信息比较丰富,表达效果好
缺点:
- 需要调参,需要大量样本,训练迭代次数比较多,最好使用GPU训练
- 物理含义不明确,从每层输出中很难看出含义来
卷积神经网络的层级结构:
- 数据输入层/ Input layer
- 卷积计算层/ CONV layer
- ReLU激励层 / ReLU layer
- 池化层 / Pooling layer
- 全连接层 / FC layer
对于各层简单的理解:
- 输入层:
- 你得到了一张大小为
227x227的彩色图片。这就是你的第一条线索- 卷积层(Convolutional Layers):
- 首先,你通过一个放大镜(或者说滤波器)仔细查看图片。这个放大镜能帮你发现图片中的一些简单的形状,比如边缘和纹理。这就是第一个卷积层的工作
- 你持续使用不同类型的放大镜来查看图片,逐步发现更多的细节。例如,你可能从简单的边缘和纹理中发现了一些更复杂的形状,如角落或某种纹理的组合。这代表了更深的卷积层
- 池化层(Pooling Layers):
- 在检查了这么多细节后,你决定摒弃一些不重要的信息,只保留最重要的线索。这就像是你在查看一张地图时,决定忽略一些小街道,只关注主要的道路。这个过程就是池化
- 全连接层(Fully Connected Layers):
- 经过多次的放大查看和筛选后,你已经收集了很多重要的线索。现在,你需要将这些线索组合起来,推理出图片的内容。这就是全连接层的工作,它会连接之前所有提取的信息,帮助你做出最后的决策
- 输出层:
- 最后,你基于收集的所有线索,做出了你的判断:这张图片是一只猫、一辆车、还是一个人?
输入层(Input layer)
去均值:把输入数据各个维度都中心化为0,如下图所示,其目的就是把样本的中心拉回到坐标系原点上。
归一化:幅度归一化到同样的范围,如下所示,即减少各维度数据取值范围的差异而带来的干扰,比如,我们有两个维度的特征A和B,A范围是0到10,而B范围是0到10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即A和B的数据都变为0到1的范围。
PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化
白化:深度学习的预处理:从协方差矩阵到图像白化 - 知乎 (zhihu.com)
去均值与归一化效果图:

去相关与白化效果图:
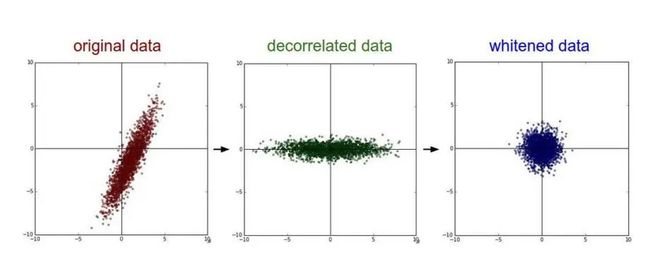
卷积层(CONV layer)
卷积层的作用
在这个卷积层,有两个关键操作:
局部关联,每个神经元看做一个滤波器(filter)
窗口(receptive field)滑动, filter 对局部数据计算
- 局部感知:在处理图像时,每个神经元不是与前一层的所有神经元相连,而只是与一个小的局部区域相连。这可以捕捉图像中的局部特征
- 权重共享:卷积层中的神经元使用相同的权重和偏差。这意味着,不同的神经元都会对相同的局部特征进行检测,但在不同的位置。这大大减少了模型的参数量,并增强了模型的空间不变性
- 平移不变性:由于权重共享,卷积神经网络可以在图像的任何位置检测到特定的特征,从而实现了平移不变性
- 多个卷积核:一个卷积层可以包含多个卷积核(也叫滤波器),每个滤波器都可以检测不同的特征,例如边缘、纹理等
神经元的空间排列
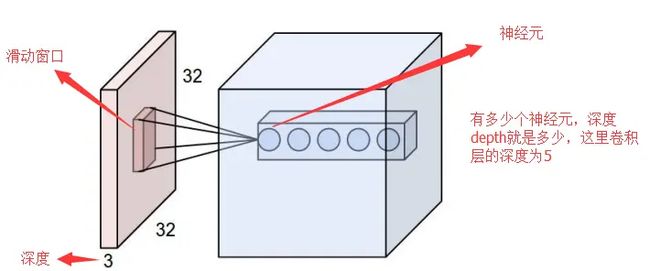
感受野讲解了卷积层中每个神经元与输入数据体之间的连接方式,但是尚未讨论输出数据体中神经元的数量,以及它们的排列方式。3个超参数控制着输出数据体的尺寸:深度(depth),步长(stride)和零填充(zero-padding
深度(depth)
步长(stride)
有时也需要通过设置步幅 (Stride) 来压缩⼀部分信息。步幅表⽰核在原始图⽚的⽔平⽅向和垂直⽅向上每次移动的距离。使⽤卷积步幅,跳过核中的⼀些位置 (看作对输出的下采样) 来降低计算的开销
在⾼上步幅为 3、在宽上步幅为 2 的卷积操作。当输出第⼀列第⼆个元素时,卷积窗⼜向下滑动了 3 ⾏,⽽在输出第⼀⾏第⼆个元素时卷积窗⼜向右滑动了 2 列。通常我们设置在⽔平⽅向和垂直⽅向的步幅⼀样,如果步幅设为 s,则输出尺⼨为:
⌊ m + 2 p − f s + 1 ⌋ , ⌊ n + 2 p − f s + 1 ⌋ \lfloor{\frac{m+2p-f}{s}}+1\rfloor,\lfloor{\frac{n+2p-f}{s}}+1\rfloor ⌊sm+2p−f+1⌋,⌊sn+2p−f+1⌋
填充(padding)
假设输⼊图⽚的⼤⼩为 (m, n),⽽卷积核的⼤⼩为 (f, f),则卷积后的输出图⽚⼤⼩为 (m−f + 1*, n−f* + 1),由此带来两个问题:
- 每次卷积运算后,输出图⽚的尺⼨缩⼩
- 原始图⽚的⾓落、边缘区像素点在输出中采⽤较少,输出图⽚丢失很多边缘位置的信息
因此可以在进⾏卷积操作前,对原始图⽚在边界上进⾏填充 (Padding),以增加矩阵的⼤⼩,通常将 0 作为填充值
设每个⽅向扩展像素点数量为 p,则填充后原始图⽚的⼤⼩为 (m + 2p, n + 2p),卷积核⼤⼩保持 (f, f) 不变,则输出图⽚⼤⼩ (m + 2p−f + 1*, n* + 2p−f + 1)。常⽤填充的⽅法有:
- **有效 (valid) 卷积:不填充,直接卷积,结果⼤⼩为 (m − f + 1, n−f + 1)
- **相同 (same) 卷积:**⽤ 0 填充,并使得卷积后结果⼤⼩与输⼊⼀致,这样 p = (f−1)/2
- **全 (full) 卷积:通过填充,使得输出尺⼨为 (m + f − 1, n + f − 1)
几种不同卷积简介
扩张卷积 (Dilated Convolution)
扩张卷积,也称空洞卷积,它引⼊的参数被称为扩张率 (Dilation rate),其定义了核内值之间的间距。如图所⽰,图中扩张速率为 2 的 3×3内核将具有与 5×5 内核相同的视野,但只使⽤ 9 个参数。这种⽅法能以相同的计算成本,提供更⼤的感受野-点击跳转感受野。在需要更⼤的观察范围,且⽆法承受多个卷积或更⼤的内核,可以⽤它
如果输⼊图⽚的⼤⼩为 (m, n),⽽卷积核的⼤⼩为 (f, f),每个⽅向扩展像素点数量为 p,步幅设为 s,则标准卷积输出尺⼨为 ⌊ m + 2 p − f s + 1 ⌋ , ⌊ n + 2 p − f s + 1 ⌋ \lfloor{\frac{m+2p-f}{s}}+1\rfloor,\lfloor{\frac{n+2p-f}{s}}+1\rfloor ⌊sm+2p−f+1⌋,⌊sn+2p−f+1⌋。如果扩张率为 r,则扩张卷积输出尺⼨为$\lfloor\frac{m+2p-[f+(f-1)(r-1)]}s+1\rfloor,\lfloor\frac{n+2p-[f+(f-1)(r-1)]}s+1\rfloor $

分别显⽰了不考虑扩张率 (默认为 1),以及考虑扩张率 (为 2 和 3) 的效果
分组卷积
分组卷积 (Group Convolution)
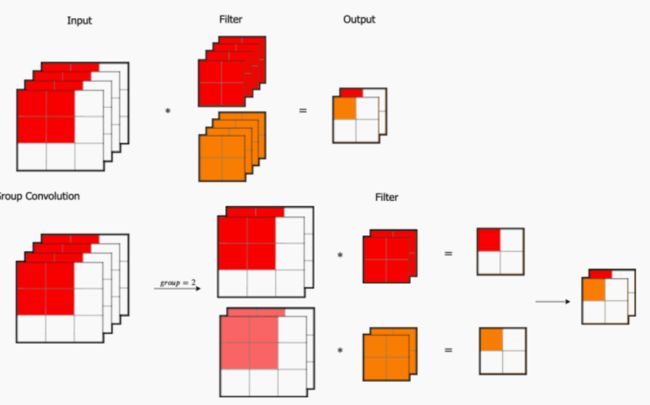
- 我们先考虑标准卷积,对输⼊为 3×3×4 的数组,经过 2 组 2×2×4 的卷积核,得到 2×2×2 的输出。这⾥我们⼀共需要 2×2×4×2=32个参数。
- 我们将输⼊数组依据通道分为 2 组,每组需要 2×2×2 的卷积核就可以得到 2×2×1 的输出,拼接在⼀起同样得到 2×2×2 的输出。在这个分组卷积中,我们⼀共需要 2×2×2×2=16 个参数
深度可分离卷积
深度可分离卷积 (Depthwise Separable Convolution)
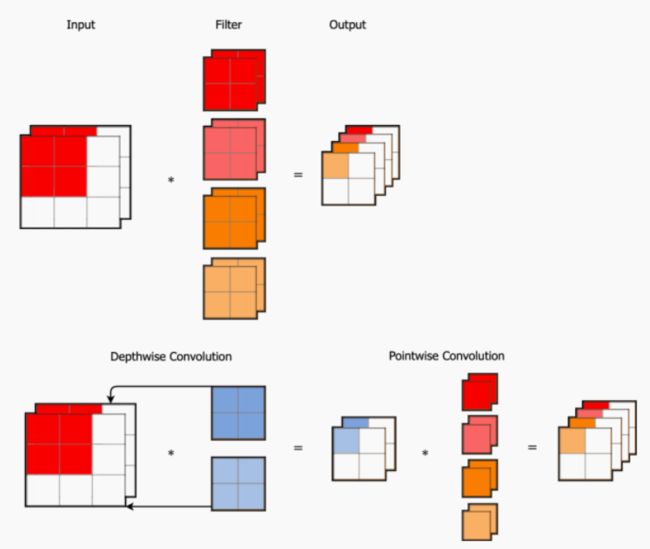
对输⼊ 3×3×2 的数组,经过 4 组 2×2×2 的卷积核,得到 2×2×4 的输出。这⾥我们⼀共需要 2×2×2×4=32 个参数
我们使⽤深度可分离卷积,它将卷积过程分成两个步骤:
- 第⼀步,在 Depthwise Convolution,输⼊有⼏个通道就设⼏个卷积核,如图所⽰,输⼊⼀共 2 个通道,对每个通道分配⼀个卷积核,这⾥的每个卷积核只处理⼀个通道 (对⽐原始卷积过程每组卷积核处理所有通道)
- 第⼆步,在 Pointwise Convolution,由于在上⼀步不同通道间没有联系,因此这⼀步⽤ 1×1 的卷积核组来获得不同通道间的联系。我们可以看出,在深度可分离卷积中,我们⼀共需要2×2×2+1×1×2×4=16 个参数
池化层(Pooling layer)
池化层作用
考虑到要描述⼀个⼤图像,⼀个⾃然的⽅法是在不同位置处对特征进⾏汇总统计
- 池化层用于在卷积神经网络上减小特征空间维度,但不会减小深度
- 池化层的核心目标之一是提供空间方差,这意味着你或机器将能够将对象识别出来,即使它的外观以某种方式发生改变
- 特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征
- 特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用
- 在一定程度上防止过拟合,更方便优化
池化层分类
池化函数是使⽤某⼀位置的相邻输出的总体统计特征来代替⽹络在该位置的输出
- 最大池化函数 (Max Pooling) 给出相邻矩形区域内的最⼤值
- 平均池化 (Average Pooling) 计算相邻矩形区域内的平均值
- 其他常⽤的池化函数包括 L2 范数以及基于距中⼼像素距离的加权平均函数
池化层特点
- 不管采⽤什么样的池化函数,当输⼊作出少量平移时,池化能够帮助输⼊的表⽰近似不变。平移的不变性是指当我们对输⼊进⾏少量平移时,经过池化函数后的⼤多数输出并不会发⽣改变
- 局部平移不变性是⼀个很有⽤的性质,尤其是当我们关心某个特征是否出现而不关心它出现的具体位置时
卷积与池化作为一种无限强的先验:
卷积和池化在卷积神经网络(CNN)中起到了很重要的作用,它们都可以被视为某种形式的先验假设(prior)对于处理图像或其他类似的网格数据。具体来说:
- 卷积作为先验:
- 局部性: 卷积运算考虑的是输入数据的一个小的局部区域,这对应于一个先验的信念,即在图像或其他类似的数据中,局部的信息通常是有意义的
- 参数共享: 卷积层的权重是在空间上共享的,这意味着对于图像中的特定特征,不管它出现在哪个位置,都使用同样的权重进行检测。这反映了一个先验的信念,即图像中的某个特征在空间上的不同位置都是有意义的
- 池化作为先验:
- 不变性: 池化,尤其是最大池化,提供了对小的平移变化的不变性。这基于一个先验的信念,即小的平移通常不会改变物体的类别或特征的性质
- 下采样: 通过池化减少数据的维度,这表示了一个信念,即可以通过丢弃一些空间分辨率来保留最重要的信息
当我们说卷积和池化是"无限强的先验"时,这意味着这些操作或假设是固定的并且非常受限制的,它们为模型处理图像数据提供了一个特定的方式。这种先验的选择使CNN在图像处理任务上表现出色,但这也限制了它们在不满足这些先验的其他任务上的适用性
不过,值得注意的是,虽然这些先验在图像处理上非常有效,但它们并不是万能的。为了处理更复杂或不同类型的数据和任务,研究人员已经开始探索不同类型的网络结构和先验
感受野
感受野介绍
跳转到参考链接
在卷积神经网络中,决定某一层输出结果中一个元素所对应的输入层的区域大小,被称作感受野(receptive field)通俗的解释是,输出feature map上的一个单元对应输入层上的区域大小

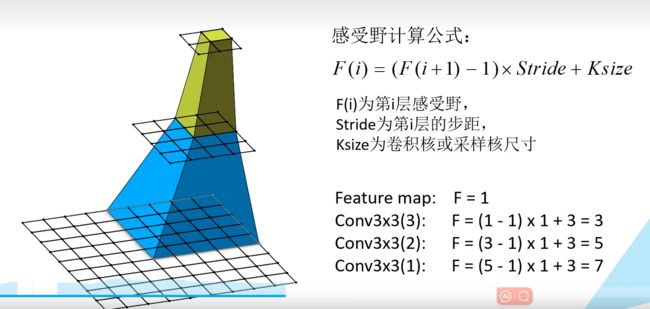
感受野计算
计算实例
实例1:
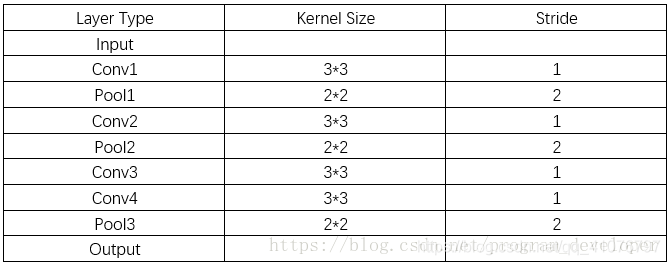
根据上面的规律,我们可以计算:
- r 0 = 1 , s 0 = 1
- r 1 = 3
- r 2 = 3 + ( 2 − 1 ) ∗ 1 = 4(r2即对应pool1层)
- r 3 = 4 + ( 3 − 1 ) ∗ 2 = 8
- r 4 = 8 + ( 2 − 1 ) ∗ 2 = 10 (r4即对应pool2层)
- r 5 = 10 + ( 3 − 1 ) ∗ 4 = 18
- r 6 = 18 + ( 3 − 1 ) ∗ 4 = 26 (r6即对应conv4层)
- r 7 = 26 + ( 2 − 1 ) ∗ 4 = 30
实例2-VGG16(后面会介绍):

conv1_1: RF=3
conv1_2: RF=3+(3-1)*1=5
pool1: RF=5+(2-1)*1=6
conv2_1: RF=6+(3-1)*2=10
…
后面的数在上图的栏目里都有了,就不一一计算了,最终结果也是212
卷积神经网络中的不变性
卷积神经网络(CNN)在计算机视觉领域已经取得了显著的成功,这要归功于其能够学习到平移、尺度、和形变的不变性。以下是CNN如何通过局部感受野、权重共享和下采样来实现这些不变性的:
- 局部感受野 (Local Receptive Fields)
- 解释:局部感受野意味着每一个神经元只“看”输入数据的一个小部分(例如一个小的像素块)。在图像处理中,这通常对应于一个小的方形区域
- 如何保证不变性
- 平移不变性:由于神经元在局部范围内操作,所以即使图像发生小的平移,仍然可以检测到相同的特征
- 形变的不变性:局部特征可以捕捉图像中的微小形变,而不受全局形变的影响
- 权重共享 (Shared Weights)
- 解释:在卷积层中,所有的神经元都使用相同的权重和偏置,这被称为卷积核或滤波器
- 如何保证不变性
- 平移不变性:由于权重共享,无论特征在图像的哪个位置,都可以使用相同的卷积核来检测它。这意味着,如果图像中的某个特征发生平移,权重共享可以确保我们仍然能够检测到它
- 下采样 (Sub-sampling)
- 解释:下采样通常在池化层中进行,例如最大池化或平均池化,它会减少特征图的尺寸,从而减少计算量
- **目的:**减少特征图的空间尺寸以节省计算资源,同时增加其感受野,从而捕获更大范围内的上下文信息
- 如何保证不变性
- 平移不变性:即使在小的平移下,通过下采样,特征在特征图的相对位置可能不会发生显著变化
- 尺度的不变性:下采样使得网络能够在不同尺度上识别类似的结构或模式
- 形变的不变性:池化层提供了对小的形变的鲁棒性,因为它们通常选择最显著的特征(如在最大池化中)或者取平均值(在平均池化中)
结合上述三种架构思想,卷积神经网络能够有效地识别和处理图像中的平移、尺度和形变,确保在各种变化和扭曲下都具有良好的性能
非线性映射函数
激活函数作用
激活函数为网络提供了非线性性质,使得网络能够拟合和学习更复杂的函数和数据模式。以下是激活函数的一些主要作用:
- 引入非线性:不带激活函数的神经网络,无论其深度如何,都只是一个线性变换器,因此只能表示线性关系。通过在神经元输出上应用激活函数,网络可以表示非线性映射
- 决策边界:非线性激活函数允许神经网络创造更复杂的、非线性的决策边界,从而更好地区分数据
- 激活与去激活神经元:某些激活函数(例如ReLU)可以“关闭”某些神经元,使其在特定的输入下不激活。这可以帮助网络在某种程度上实现稀疏性,并可能提高网络的效率
- 归一化输出:某些激活函数,例如Sigmoid和Tanh,会将输出压缩到一个固定的范围内,例如0,10,1或−1,1−1,1。这可以帮助在网络的深层中保持数值稳定性
- 避免梯度问题:某些新型激活函数,如ReLU及其变体(如Leaky ReLU、Parametric ReLU、Exponential LU等),被设计为解决传统激活函数(如Sigmoid和Tanh)的梯度消失或爆炸问题
- 增加模型的表达能力:通过为不同的层选择不同的激活函数,可以增加模型的表达能力和复杂性
激活函数的选择通常取决于具体的应用和模型的要求。例如,对于二元分类问题,输出层可能会使用Sigmoid激活函数;而对于多类分类问题,输出层可能会使用Softmax激活函数。而在隐藏层中,ReLU及其变体由于其计算效率和效果而变得越来越受欢迎
几种激活函数
Sigmoid激活函数
**优点:**取值范围(0~1)、简单、容易理解
**缺点:**容易饱和和终止梯度传递(“死神经元”);sigmoid函数的输出没有0中心化
s i g m o i d = f ( x ) = 1 1 + e − x f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) \begin{aligned}sigmoid&=f\big(x\big)=\frac{1}{1+e^{-x}}\\f'\big(x\big)&=f\big(x\big)\big(1-f\big(x\big)\big)\end{aligned} sigmoidf′(x)=f(x)=1+e−x1=f(x)(1−f(x))
Tanh激活函数
**优点:**取值范围(-1~1)、易理解、0中心化
**缺点:**容易饱和和终止梯度传递(“死神经元”)
t a n h = f ( x ) = e x − e − x e x + e − x f ′ ( x ) = 1 − f ( x ) 2 \begin{aligned} &\mathrm{tanh}=f\bigl(x\bigr)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \\ &f'\bigl(x\bigr)=1-f\bigl(x\bigr)^2 \end{aligned} tanh=f(x)=ex+e−xex−e−xf′(x)=1−f(x)2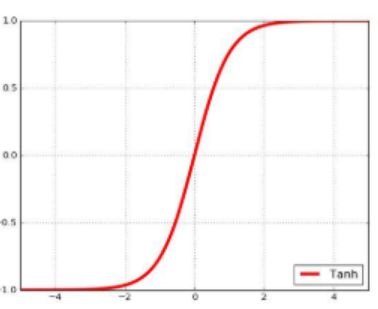
ReLU
对于输入的x以0为分界线,左侧的均为0,右侧的为y=x这条直线
缺点:
- 没有边界,可以使用变种ReLU: min(max(0,x), 6)
- 比较脆弱,比较容易陷入出现”死神经元”的情况
解决方案:较小的学习率优点:
相比于Sigmoid和Tanh,提升收敛速度
梯度求解公式简单,不会产生梯度消失和梯度爆炸
单侧抑制
稀疏激活性
ReLU = f ( x ) = max ( 0 , x ) f ′ ( x ) = { 1 , x > 0 0 , x ≤ 0 \text{ReLU}=f\big(x\big)=\max\big(0,x\big)\quad f'\big(x\big)=\begin{cases}1,x>0\\0,x\leq0\end{cases} ReLU=f(x)=max(0,x)f′(x)={1,x>00,x≤0
激励层建议
CNN尽量不要使用sigmoid,如果要使用,建议只在全连接层使用
首先使用ReLU,因为迭代速度快,但是有可能效果不佳
如果使用ReLU失效的情况下,考虑使用Leaky ReLu,此时一般情况都
可以解决啦
tanh激活函数在某些情况下有比较好的效果,但是应用场景比较少
第二版建议:
- Sigmoid函数:
- 建议在二分类问题中的输出层使用,将输出映射到[0,1]的概率范围内
- 不建议在隐藏层使用,因为其导数在两个极端值上接近于0,容易导致梯度消失问题
- Tanh函数:
- 建议在多分类问题的输出层使用,将输出映射到[-1,1]的范围内
- 可以在隐藏层中使用,但要注意梯度消失问题,因为它的导数在两个极端值上接近于0
- ReLU函数 (Rectified Linear Unit):
- 建议在隐藏层中使用,因为它具有良好的非线性特性,并且计算效率高
- 可以通过解决梯度消失问题来训练更深的神经网络
- 缺点是对于负值输入,ReLU的导数为0,可能导致部分神经元无法更新
- Leaky ReLU函数:
- 类似于ReLU,但在负值区域有一个小的斜率,这有助于解决ReLU负值区域的问题
- 建议在ReLU不适用的情况下使用,尤其是对抗生成网络(GAN)等需要稳定性的任务
- Softmax函数:
- 建议在多分类问题的输出层中使用,将输出转化为概率分布,方便进行多分类任务的概率预测
优化器
优化器在神经网络中主要用于调整模型的参数以最小化损失函数。以下是一些常见的优化器及其特性:
SGD (随机梯度下降)
- 基本且经典的优化方法
- 易受样本噪声的影响
- 可能陷入局部最优解
Momentum

ν t = η ⋅ ν t − 1 + α ⋅ g ( w t ) w t + 1 = w t − ν t \begin{aligned}\nu_t&=\eta\cdot\nu_{t-1}+\alpha\cdot g(w_t)\\w_{t+1}&=w_t-\nu_t\end{aligned} νtwt+1=η⋅νt−1+α⋅g(wt)=wt−νt
a为学习率,g(w,)为t 时刻对参数w,的损失梯度(0.9)为动量系数考虑上一层的方向
- 基于SGD,但考虑了过去的梯度以加速优化
- 通常比纯SGD更快收敛
Adagrad
s t = s t − 1 + g ( w t ) ⋅ g ( w t ) w t + 1 = w t − α s t + ε ⋅ g ( w t ) \begin{aligned} &s_{t}=s_{t-1}+g(w_{t})\cdotp g(w_{t}) \\ &w_{t+1}=w_{t}-\frac{\alpha}{\sqrt{s_{t}+\varepsilon}}\cdot g(w_{t}) \end{aligned} st=st−1+g(wt)⋅g(wt)wt+1=wt−st+εα⋅g(wt)
a为学习率,g(w,)为t 时刻对参数w,的损失梯度e(10-7)为防止分母为零的小数
缺点:过早的停止迭代
- 为每个参数动态地调整学习率
- 在训练过程中自动减少学习率,可能过早地终止更新
RMSprop
s t = η ⋅ s t − 1 + ( 1 − η ) ⋅ g ( w t ) ⋅ g ( w t ) w t + 1 = w t − α s t + ε ⋅ g ( w t ) \begin{aligned} &s_{t}=\eta\cdot s_{t-1}+(1-\eta)\cdot g(w_{t})\cdot g(w_{t}) \\ &w_{t+1}=w_{t}-\frac{\alpha}{\sqrt{s_{t}+\varepsilon}}\cdot g(w_{t}) \end{aligned} st=η⋅st−1+(1−η)⋅g(wt)⋅g(wt)wt+1=wt−st+εα⋅g(wt)
a为学习率,g(w,)为t 时刻对参数w,的损失梯度(0.9)控制衰减速度,e(10-7)为防止分母为零的小数
- 改进了Adagrad的方法,避免过早地减少学习率
- 在非平稳目标上表现出色
Adam
m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g ( w t ) 一阶动量 ν t = β 2 ⋅ ν t − 1 + ( 1 − β 2 ) ⋅ g ( w t ) ⋅ g ( w t ) 二阶动量 m ^ t = m t 1 − β 1 t ν ^ t = ν t 1 − β 2 t w t + 1 = w t − α ν ^ t + ε m ^ t \begin{aligned} &m_{t}=\beta_{1}\cdot m_{t-1}+(1-\beta_{1})\cdot g(w_{t})\quad\text{一阶动量} \\ &\nu_{t}=\beta_{2}\cdot\nu_{t-1}+(1-\beta_{2})\cdot g(w_{t})\cdot g(w_{t})\quad\text{二阶动量} \\ &\hat{m}_{t}=\frac{m_{t}}{1-\beta_{1}^{t}}\quad\hat{\nu}_{t}=\frac{\nu_{t}}{1-\beta_{2}^{t}}\\ &w_{t+1}=w_t-\frac\alpha{\sqrt{\hat{\nu}_t+\varepsilon}}\hat{m}_t \end{aligned} mt=β1⋅mt−1+(1−β1)⋅g(wt)一阶动量νt=β2⋅νt−1+(1−β2)⋅g(wt)⋅g(wt)二阶动量m^t=1−β1tmtν^t=1−β2tνtwt+1=wt−ν^t+εαm^t
a为学习率,g(w;)为t 时刻对参数w,的损失梯度B(0.9)、B,(0.999)控制衰减速度,e(10-7)为防止分母为零的小数

- 结合了Momentum和RMSprop的思想
- 在众多任务上都有出色的表现,通常是首选的优化器
通用矩阵乘(GEMM)
跳转到参考链接
通用矩阵乘 (General Matrix Multiplication,GEMM) 是深度学习的核⼼
前⾯的全连接层是通过矩阵乘实现的,卷积层是否也可以这样实现?
卷积核是在输⼊图像上按步长滑动,每次滑动操作在输⼊图像上的对应窗的区域,将卷积核中的各个权值 w与输⼊图像上对应窗⼜中的各个值x相乘,然后相加得到输出特征图上的⼀个值。卷积核对输⼊图像的每⼀次运算,可以看作是两个向量的内积,这意味着卷积操作完全可以转化为矩阵的乘法来实现
我们将卷积层的卷积操作转化为卷积核的权值矩阵与输⼊数组转化的输⼊矩阵进⾏相乘:
卷积核组:(c2*, c1,* K*,* K),单组卷积核 Kernel 的⼤⼩为 (c1*,* K*,* K)
输⼊数组:(c1*,* Hin,Win)
图中单组卷积核 Kernel 在输⼊图像上滑动得到各个 Patch∗*,Patch∗ 的⼤⼩同卷积核。我们将 Kernel 和 Patch∗* 均展开成⼀维向量。假设有 nk*(*nk= c2) 组卷积核,并且每组卷积核在输⼊上所有的滑动可以得到 np个 Patch,于是可以得到输⼊矩阵 (lcol, np) 以及权值矩阵(nk, lcol)
权值矩阵:(c2*, c*1 × K × K)
输⼊矩阵:(c1 × K × K*,* Hout × Wout)

⼀组卷积核在三维图像上滑动的过程,可以视作卷积核与输⼊图像上不同的块分别做运算。基于块可以将输⼊图像数组转化为 (lcol, np)。如果有 nk 组卷积核,将卷积核组转化为 (nk, lcol)
再具体看⼀下 Kernel 和 Patch 的展开过程。对于 Kernel,我们可以依图所⽰展开,图中所⽰为 1 组卷积核有 3 个通道,将卷积核先依通道再依⾏依次放⼊
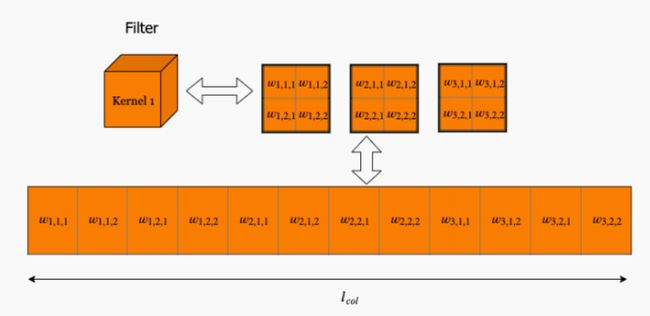
⽽每个 Patch 是 Kernel 在输⼊上滑动得到的
Flatten层与全连接层(FC layer)
通过多层卷积层/池化层后我们可以获得很多个特征图 (Feature Map),这些特征图从不同⾓度得到模型的特征,但是我们⽆法直接⽤这些特征图拿来连接到分类
对于⼀个分类模型,我们既要综合考虑所有的特征图,又要能够连接到分类,可以考虑的⽅案就是将最后得到的特征图 “拍平” (丢到Flatten层),然后把Flatten层的输出放到全连接层⾥ (⼀般⾄少 2 层以保证全连接层能够学到拟合函数)。最后采⽤ softmax 对其进⾏分类

如果是将最后⼀层的特征图Flatten再放⼊全连接层,会存在的问题是输⼊的参数量过⼤,这会降低训练的速度,同时很容易过拟合。既然是针对这些特征图进⾏分类,那么另外⼀种可以考虑的⽅案是全局平均池化 (Global Average Pooling)。如图所⽰,GAP 的操作是将最后⼀层的特征图取均值。我们得到的 GAP 层中的每个节点对应不同的特征图,连接 GAP 层和最后的密集层的权重编码了每个特征图对预测⽬标分类的贡献
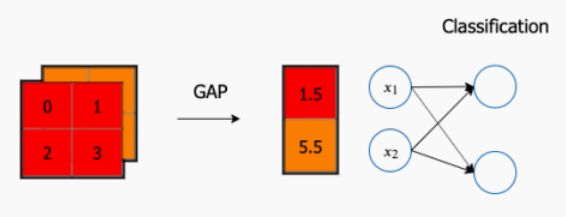
全连接与卷积转换
将卷积层转化成全连接层
- 卷积层
- 使用一个或多个卷积核(过滤器)来扫描输入特征图(例如,图像)
- 在每个位置,卷积核与输入的一个局部区域执行元素级的乘法和加法操作
- 结果形成了输出特征图
- 因此,卷积层的权重是局部的,并且具有空间共享性
- 全连接层
- 每一个输入神经元都与每一个输出神经元连接
- 通常用于神经网络的最后几层,用于分类或回归任务
如何将卷积层转化成全连接层?
- 定位卷积操作
- 首先,选择输入特征图上的一个局部区域,这个区域的大小应与卷积核相同
- 这个局部区域的每一个像素值会与卷积核中的对应值相乘,并求和得到一个输出值
- 在全连接的视角中,这相当于这个局部区域的每个像素值与输出层的一个神经元相连接,并有一个权重
- 展开操作
- 将输入特征图展开成一个长向量
- 对于每个卷积核,也将其展开成一个向量,并将其看作全连接层的权重
- 连接
- 展开后的输入向量与每一个卷积核的向量进行点积运算
- 在全连接层的视角中,这就相当于输入层与输出层的神经元之间完全连接
卷积操作可以转化为全连接操作,但两者在实际应用中的效果和用途是不同的。卷积层由于其权重共享和局部连接的特性,对于处理具有空间结构的数据(例如图像)更为高效。而全连接层则更多地用于数据的整合和高级特征的学习
将全连接层转化成卷积层
为了理解这种转化,首先要明确一个全连接层是如何工作的。假设有一个全连接层,其输入维度为H,W,C(高、宽、通道数),输出有D个神经元。这意味着该层有H×W×C×D个权重
现在,如果你想将这个全连接层转换为一个卷积层,你可以这样做:
- 确定卷积核的大小:这通常是根据全连接层的输入维度来的。如果输入是一个H,W,C的特征图,那么卷积核的大小就是H*,W
- 设置卷积核的数量:这等于全连接层的输出神经元数量,即D
- 权重复制:全连接层的权重可以直接复制到新的卷积层中。每一个输出神经元对应的权重变为卷积核中的一个权重。
这样,当你用一个H,W,C大小的输入特征图对这个新的卷积层进行前向传播时,你会得到一个1,1,D大小的输出。从本质上看,这与原始的全连接层给出的输出是一样的,但这种表示形式使得网络更具模块化和灵活性。
为什么这样做有用?
- 空间映射:全卷积网络可以接受任意大小的输入,生成对应的空间大小的输出。这对于语义分割等任务特别有用,因为模型可以为输入图像的每一个像素生成一个标签
- 参数数量不变:虽然我们从全连接层转到了卷积层,但参数的数量并没有改变
- 更多的结构灵活性:例如,你可以在这个卷积层后面加更多的卷积层,从而对空间特征进行进一步的处理
这种转化是神经网络结构设计中的一种常见技巧,尤其是在语义分割和图像到图像的转换任务中
参数初始化
跳转到参考链接
参数初始化对训练过程的收敛速度和最终的表现有很大的影响。不恰当的初始化可能导致梯度消失或梯度爆炸,从而使得网络难以训练
在卷积神经网络中,可以看到神经元之间的连接是通过权重w以及偏置b实现的。并且w和b的取值会直接影响模型的训练速度以及训练精度
权重的初始化
**建议方式:**很小的随机数(对于多层深度神经网络,太小的值会导致回传的梯度非常小)服从均值为0,方差比较小(建议:2/n, n为权重数量)的高斯分布随机数列
Xavier
服从均匀分布的随机数列,基本思想是保持输入和输出的方差一致
错误方式
全部初始化为0,全部设置为0,在反向传播的时候是一样的梯度值,那么这个网络的权重是没有办法差异化的,也就没有办法学习到东西
NOTE:
Weight Standarization(权重w标准化)类似批归一化,也是对权重系数做一个标准化的操作,让模型效果会稍微好一点,在卷积/FC操作之前,对w做一个标准化操作。在卷积操作中,以每个卷积核为单位计算均值μ、标准差σ;在FC操作,以当前层次的所有的权重为单位计算均值μ、标准差σ
偏置项的初始化
一般直接设置为0,在存在ReLU激活函数的网络中,也可以考虑设置为一个很小的数字(大于0)
归一化
内部协变量偏移
跳转到参考链接
内部协变量偏移(Internal Covariate Shift)
每个神经元的输入数据不再是“独立同分布”的后果:
- 各层参数需要不断适应新的输入数据分布,降低学习速度。(学习率不能大,训练速度缓慢)
- 深层输入的变化可能趋向于变大或者变小,导致浅层落入饱和区,使得学习过早停止。(容易梯度饱和、消失。)
- 每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能谨慎地选择。(调参困难)
- 独立同分布假设(IID):在机器学习中,经常假设训练数据和测试数据是满足相同分布的。这样做的目的是确保在训练集上训练出的模型可以在测试集上获得良好的性能
- BatchNorm的作用:BatchNorm的目的是减轻深度神经网络中的“Internal Covariate Shift”问题。通过对每一层的输入进行规范化,使其保持相同的分布,从而加速网络的训练并提高模型的稳定性
- Covariate Shift与Internal Covariate Shift:
- Covariate Shift:当输入数据的分布发生变化,但输出的条件分布保持不变时,会出现Covariate Shift。这种情况下,机器学习模型可能需要使用迁移学习技术来调整
- Internal Covariate Shift:它是深度学习中特有的现象,是由于网络的各层参数在训练过程中持续变化导致的。这意味着在训练过程中,隐层的输入分布也会不断地变化。BatchNorm的引入就是为了解决这个问题
总的来说,为了使机器学习模型表现得更好,数据的独立同分布假设是很重要的。对于深度学习模型,由于其多层的结构,隐层输入的分布可能会随着训练的进行而发生变化,这种变化可能会导致模型训练困难。BatchNorm是为了解决这个问题而提出的,它可以稳定各层的输入分布,从而有助于加速训练并提高模型性能
解决:
Batch Normalization解决内部协变量偏移,BN的本质就是利用优化变一下方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入的数据分布基本保持一致
几种归一化展示
- BatchNorm: 对一个批次内的数据在每个特定位置(即相同的高度、宽度和通道位置)进行归一化,基于整个批次的N * H * W的数据计算均值和方差
- LayerNorm: 对单个数据样本的所有位置进行归一化,无论批次大小如何。基于C * H * W的数据计算均值和方差
- InstanceNorm: 这通常用于风格迁移任务。对单个数据样本的每个通道进行独立归一化。基于H * W的数据计算均值和方差
- GroupNorm: 通道被分为多个组,并且在每个组内的位置上进行归一化。如果将通道数量C分为G个组,则每个组的归一化基于(C//G) * H * W的数据
归一化主要有以下几个原因:
- 噪声减少:噪声是数据中不必要的或误导性的信息,通常是由于数据的不完整性或不一致性造成的。标准化可以将数据转化为统一的尺度,从而在分析时减少噪声的影响
- 消除偏差和异常值:偏差和异常值可能会扭曲数据分析的结果。标准化方法,特别是z-score标准化,可以将数据转化为均值为0,方差为1的分布,有助于识别和处理这些偏差和异常值
- 提高可解释性和可比性:不同的数据源或测量单位可能导致数据在尺度或范围上存在差异,这会使得数据比较和解释变得困难。标准化通过将数据转化为相同的尺度或范围,简化了数据的比较和解释过程
【扩展】
- 算法性能的提高:很多机器学习算法,特别是基于梯度下降的算法如神经网络、支持向量机等,在标准化的数据上通常会有更快的收敛速度和更好的性能
- 特征权重的平衡:在某些机器学习模型中,如线性回归,未标准化的特征因为其尺度差异可能会对模型的预测产生不均衡的影响。标准化可以确保所有特征在模型中有均等的权重
- 提高数据的鲁棒性:标准化可以增加模型对小的数据波动的鲁棒性,从而使模型更加稳定
总之,数据标准化是数据预处理中的一个关键步骤,对于保证数据的质量、提高模型的性能和稳定性具有重要的作用
批归一化
具体步骤
批归一化(Batch Normalization Layer)
BN的训练步骤主要分为以下4步:
求解每个训练批次数据的均值
求解每个训练批次数据的方差
使用求得的均值和方差对该批次的数据做标准化处理,获得0-1分布
尺度变换和偏移:使用标准化之后的x乘以γ调整数值大小,再加上β增加偏移后得到输出值y。这个γ是尺度因子,β是平移因子,属于BN的核心精髓,由于标准化后的x基本会被限制在正态分布下,会使得网络的表达能力下降,为了解决这个问题,引入两个模型参数γ、β进行平移变化
BN中的γ和β的作用:
保证了模型的capacity,意思就是,γ和β作为调整参数可以调整被BN刻意改变过后的输入,即能够保证能够还原成原始的输入分布。BN对每一层输入分布的调整有可能改变某层原来的输入,当然有了这两个参数,经过调整也可以不发生改变,既可以改变同时也可以保持原输入,那么模型的容纳能力(capacity)就提升了
适应激活函数,如果是sigmoid函数,那么BN后的分布在0-1之间,由于sigmoid在接近0的地方趋于线性,非线性表达能力可能会降低,因此通过γ和β可以自动调整输入分布,使得非线性表达能力增强
如果激活函数为ReLU,那么意味着将有一半的激活函数无法使用,那么通过β可以进行调整参与激活的数据的比例,防止dead-Relu问题
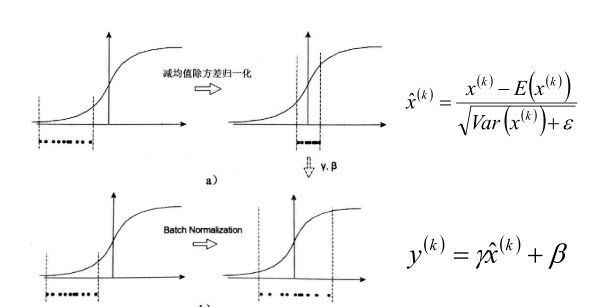
注意:在训练的时候我们一般使用一个批次中的样本的均值和标准差进行BN操作,但是预测的时候由于样本数目不确定(比较少),所以不好使用预测样本的均值和方差进行BN操作,实际上在预测的时候,使用的是训练阶段所有batch记录下来的均值和方差的期望值作为预测时候BN的均值和方差
E [ x ] = E B [ μ B ] V a r [ x ] = m m − 1 E B [ σ B 2 ] y = γ V a r [ x ] + ε x + ( β − γ E ( x ) V a r [ x ] + ε ) \begin{aligned}&E\Big[x\Big]=E_{B}\Big[\mu_{B}\Big]\\&Var\Big[x\Big]=\frac{m}{m-1}E_{B}\Big[\sigma_{B}^{2}\Big]\end{aligned} \quad y=\frac{\gamma}{\sqrt{Var\Big[x\Big]+\varepsilon}}x+\left(\beta-\frac{\gamma E\Big(x\Big)}{\sqrt{Var\Big[x\Big]+\varepsilon}}\right) E[x]=EB[μB]Var[x]=m−1mEB[σB2]y=Var[x]+εγx+ β−Var[x]+εγE(x)

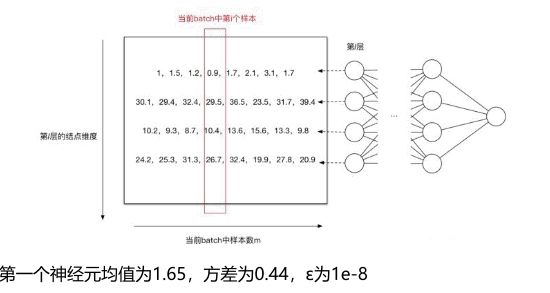

在CNN中,由于CNN的特征是对应到一个feature map特征图上的,所以在CNN中做BN的时候不是以神经元作为单位,而是以feature map特征图作为单位的。也就是针对一个批次中的一个channel的所有feature map计算一对参数γ、β。这样可以减少模型参数的数目
假设现在batch_size=8,feature map的大小为32 * 32, feature map数量为10个,传统的BN参数量为: 20480,CNN中的BN参数量为:20
优缺点
Batch Normalization优点:
- 加速收敛,可以使网络更快地收敛,这意味着需要较少的训练周期
- 具有一定的正则化效果,类似Dropout、L1、L2等正则化的效果
- 对于模型参数的初始化方式和模型参数取值不太敏感,使得网络学习更加稳定,提高模型训练精度
Batch Normalization缺点:
- 增加了模型复杂性,引入额外的参数(平均值和方差)和计算步骤,这可能会使训练时间稍微增加
- 对batchsize大小敏感,由于每次计算均值和方差是在同一个batch上,如果batchsize设置的太小,计算出来的均值和方差不足以代表整个数据分布
- BN的计算过程中需要保存某一层神经网络batch的均值和方差等统计信息,对于固定长度的网络结构(DNN、CNN)比较适合,但是对于不定长度的RNN的,训练比较麻烦
层归一化
层归一化(Layer Normalizaiton)
BN特别依赖batch Size,所以接下来提出Layer Normalizaiton,一张图片计算一组均值和方差,使得LN不受batch size的影响。同时,LN可以很好地用到序列型网络RNN中
没有正则化效果:与BatchNorm不同,LayerNorm没有批内的噪声引入,因此没有明显的正则化效果
**主要优点:**不受样本批次大小的影响。在RNN上效果比较明显,但是在CNN上,效果不及BN
μ l = 1 H ∑ i = 1 H a i l σ l = 1 H ∑ i = 1 H ( a i l − μ l ) 2 \mu^{l}=\frac{1}{H}\sum_{i=1}^{H}a_{i}^{l}\quad\sigma^{l}=\sqrt{\frac{1}{H}\sum_{i=1}^{H}\left(a_{i}^{l}-\mu^{l}\right)^{2}} μl=H1i=1∑Hailσl=H1i=1∑H(ail−μl)2
实例归一化
实例归一化(Instance Normalization)
在BN中注重对于每个batch中的数据进行归一化操作,保证数据的一致性,是因为在判别模型中的结果一般取决于数据整体分布情况
没有正则化效果
但是在图像风格化中,生成的结果主要依赖于某个图像的实例,所以对整个batch做归一化不是特别的适合,比较适合对每个feature map特征图(H W)做归一化操作,能够保证各个图像实例之间的独立
**优点:**不受样本批次大小影响,保证每个feature map的独立性
组归一化
组归一化(Group Normalization Layer)
主要针对于BN中对于小batchsize效果差的问题,在GN中将channel方向分为不同的group,然后每个group中计算归一化操作,计算(C//G)WH的均值、方差,然后进行归一化操作,这样计算出来的结果和batchsize没有关系,效果比较不错
**优点:**对于小batchsize的模型效果也非常不错

自适应的归一化
自适应的归一化(Switchable Normalization Layer)
SN自适配归一化方法,将 BN、LN、IN 结合,赋予不同权重,让网络自己去学习归一化层应该使用什么方法
h ^ n c i j = γ h n c i j − Σ k ∈ Ω w k μ k Σ k ∈ Ω w k ′ σ k 2 + ϵ + β , μ i n = 1 H W ∑ i , j H , W h n c i j , σ i n 2 = 1 H W ∑ i , j H , W ( h n c i j − μ i n ) 2 , μ l n = 1 C ∑ c = 1 C μ i n , σ l n 2 = 1 C ∑ c = 1 C ( σ i n 2 + μ i n 2 ) − μ l n 2 , μ b n = 1 N ∑ n = 1 N μ i n , σ b n 2 = 1 N ∑ n = 1 N ( σ i n 2 + μ i n 2 ) − μ b n 2 , \begin{aligned} &\hat{h}_{ncij}=\gamma\frac{h_{ncij}-\Sigma_{k\in\Omega}w_{k}\mu_{k}}{\sqrt{\Sigma_{k\in\Omega}w_{k}^{\prime}\sigma_{k}^{2}+\epsilon}}+\beta, \\ &\mu_{\mathrm{in}} =\quad\frac{1}{HW}\sum_{i,j}^{H,W}h_{ncij},\quad\sigma_{\mathrm{in}}^{2}=\frac{1}{HW}\sum_{i,j}^{H,W}(h_{ncij}-\mu_{\mathrm{in}})^{2}, \\ &\mu_{\mathrm{ln}} =\quad\frac{1}{C}\sum_{c=1}^{C}\mu_{\mathrm{in}},\quad\sigma_{\mathrm{ln}}^{2}=\frac{1}{C}\sum_{c=1}^{C}(\sigma_{\mathrm{in}}^{2}+\mu_{\mathrm{in}}^{2})-\mu_{\mathrm{ln}}^{2}, \\ &\mu_{\mathrm{bn}} =\quad\frac{1}{N}\sum_{n=1}^{N}\mu_{\mathrm{in}},\quad\sigma_{\mathrm{bn}}^{2}=\frac{1}{N}\sum_{n=1}^{N}(\sigma_{\mathrm{in}}^{2}+\mu_{\mathrm{in}}^{2})-\mu_{\mathrm{bn}}^{2}, \end{aligned} h^ncij=γΣk∈Ωwk′σk2+ϵhncij−Σk∈Ωwkμk+β,μin=HW1i,j∑H,Whncij,σin2=HW1i,j∑H,W(hncij−μin)2,μln=C1c=1∑Cμin,σln2=C1c=1∑C(σin2+μin2)−μln2,μbn=N1n=1∑Nμin,σbn2=N1n=1∑N(σin2+μin2)−μbn2,
正则化与Dropout
正则化
跳转到参考链接
神经网络的学习能力受神经元数目以及神经网络层次的影响,神经元数目越大,神经网络层次越高,那么神经网络的学习能力越强,那么就有可能出现过拟合的问题;(通俗来讲:神经网络的空间表达能力变得更紧丰富了)
Regularization:正则化,通过降低模型的复杂度,通过在损失函数上添加一个正则项的方式来降低overfitting,主要有L1和L2两种方式
- L1 正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2 正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
Drpout
Dropout:通过随机删除神经网络中的神经元来解决overfitting问题,在每次迭代的时候,只使用部分神经元训练模型获取W和d的值

实现过程:
- 随机概率p随机dropout部分神经元,并前向传播
- 计算前向传播的损失,应用反向传播和梯度更新(对剩余的未被dropout的神经元)
- 恢复所有神经元的,并重复过程1
Vanilla Dropout与Inverted Dropout
- Dropout的核心思想:在训练过程中,以一定的概率p随机“关闭”部分神经元。这种随机失活有助于防止特定神经元过于依赖,从而增强模型的泛化能力
- Vanilla Dropout的问题:
- 测试阶段复杂:为保证训练与测试时的分布一致性,测试时也需要应用dropout,这可能导致同一个输入在不同时间得到不同的预测
- 输出不稳定:由于测试时的随机性,模型的预测可能会变得不稳定
- Inverted Dropout:
- 目的:简化测试过程并增加稳定性
- 方法:在训练时,除了应用p的概率随机失活外,还会将活跃神经元的输出提前除以(1-p)。这相当于在训练时就对网络的分布进行了“拉伸”
- 优势:由于训练时已经“拉伸”了网络的分布,所以在测试时,无需再应用dropout或进行任何其他修改。这样,测试过程变得简单,输出也更加稳定
- Dropout的特性:Dropout不会改变输入的期望值,因此整个网络的输出分布在应用dropout前后是一致的
精华提炼:Dropout是一种有效的正则化策略,通过随机失活部分神经元来增强模型的泛化能力。但Vanilla Dropout在测试阶段可能导致输出不稳定。为解决这一问题,Inverted Dropout在训练时对活跃神经元的输出进行“拉伸”,从而在测试时无需任何修改,简化了流程并提高了输出的稳定性。重要的是,Dropout技术保证了整体输入的期望值不变
Dropout 和 DropBlock
Dropout 和 DropBlock 都是正则化技巧,用于防止深度学习模型的过拟合。但它们的操作方式和使用场景有所不同。下面是它们的比较和解释:
Dropout
- 定义:Dropout 是一个在训练过程中随机将某些神经元的输出设置为0的技术。这样做的目的是防止网络中的任何一个神经元变得过于专门化。
- 操作方式:在每次训练迭代中,每个神经元都有一个概率
p被“丢弃”,即其输出被设置为0。- 优势:
- 简单而有效。
- 能够防止模型的过拟合。
- 可以看作是在训练时对模型进行集成。
- 缺点:
- 在卷积神经网络(CNN)中,由于空间信息的重要性,传统的 Dropout 可能不是最佳选择。
DropBlock
- 定义:DropBlock 是 Dropout 的一种变种,特别适用于卷积神经网络。与随机丢弃单个元素不同,DropBlock 随机丢弃连续的区域(块)。
- 操作方式:在每次训练迭代中,随机选择一个区域(如5x5的区域)并将整个区域的值设置为0。
- 优势:
- 更适合于卷积神经网络,因为它考虑到了像素之间的空间关系。
- 提供了与传统 Dropout 相当但在某些任务上更优的正则化效果。
- 缺点:
- 相对于简单的 Dropout,实现稍微复杂一些。
总结:
- Dropout 是一个更为通用的正则化技巧,可以应用于大多数神经网络结构中。
- DropBlock 是专为卷积神经网络设计的,其目的是在保持空间一致性的同时引入正则化,尤其在深度卷积网络中表现出色
权重衰减(weight decay)
- 权重衰减weight decay,并不是一个规范的定义,而只是俗称而已,可以理解为削减/惩罚权重。在大多数情况下weight dacay 可以等价为L2正则化
- L2正则化的作用就在于削减权重,降低模型过拟合,其行为即直接导致每轮迭代过程中的权重weight参数被削减/惩罚了一部分,故也称为权重衰减weight decay
- 从这个角度看,不论你用L1正则化还是L2正则化,亦或是其他的正则化方法,只要是削减了权重,那都可以称为weight dacay
设:
- 参数矩阵为p(包括weight和bias)
- 模型训练迭代过程中计算出的loss对参数梯度为d_p
- 学习率lr
- 权重衰减参数为decay
则不设dacay时,迭代时参数的更新过程可以表示为:p= p - lr×d_p。增加weight_dacay参数后表示为:p = p - lr ×(d_p + p × dacay)
- 在深度学习框架的实现中,可以通过设置weight_decay参数,直接对weight矩阵中的数值进削减(而不是像L2正则一样,通过修改loss函数)起到正则化的参数惩罚作用
- 二者通过不同方式,同样起到了对权重参数削减/惩罚的作用,实际上在通常的随机梯度下降算法(SGD)中,通过数学计算L2正则化完全可以等价于直接权重衰减(少数情况除外,譬如使用Adam优化器时)
- 正因如此,深度学习框架通常实现weight dacay/L2正则化的方式很简单,直接指定weight_dacay参数即可
适用
- 一般都可以使用Dropout解决过拟合问题
- 回归算法中使用L2范数相比于Softmax分类器,更加难以优化
- 对于回归问题,首先考虑是否可以转化为分类问题,比如:用户对于商品的评分,可以考虑将得分结果分成1~5分,这样就变成了一个分类问题
- 如果实在没法转化为分类问题的,那么使用L2范数的时候要非常小心,比如在L2范数之前不要使用Dropout
- 一般建议使用L2范数或者Dropout来减少神经网络的过拟合
Dropout 优点:
- **减少过拟合:**通过随机地关闭一部分神经元,Dropout能够防止模型对特定训练数据过于敏感
- **作为正则化:**Dropout起到了正则化的效果,有助于简化模型结构
- **增强模型鲁棒性:**使模型对输入的小变化更加鲁棒
Dropout 缺点:
- 不适合宽度太窄的⽹络,否则⼤部分⽹络没有输⼊到输出的路径
- 不适合训练数据太⼩(如⼩于 5000)的⽹络,训练数据太⼩时,Dropout 没有其他⽅法表现好
- 不适合⾮常⼤的数据集,数据集⼤的时候正则化效果有限 (⼤数据集本⾝的泛化误差就很⼩),使⽤ Dropout 的代价可能超过正则化的好处
卷积神经网络的训练
卷积网络示意图
卷积的内部实现实际上是矩阵相乘,因此,卷积的反向传播过程实际上跟普通的全连接是类似的
CNN的基本层包括卷积层和池化层,⼆者通常⼀起使⽤ (⼀个池化层紧跟⼀个卷积层之后)。这两层包括三个级联的函数:卷积,激励函数 (如sigmoid 函数),池化。其前向传播和后向传播的⽰意图如下:
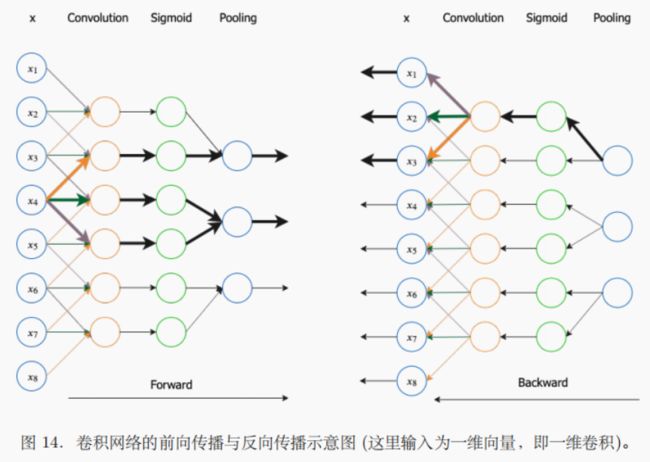
单层卷积层
卷积的导数及反向传播
从⼀维卷积⼊⼿,假设⼀个卷积过程的输⼊向量是 x,输出向量是 y,参数向量 (卷积算⼦) 是 w。从输⼊到输出的过程为: y = x ∗ w y=x*\boldsymbol{w} y=x∗w
其中 y 的长度为 |y|,y 中每⼀个元素的计算⽅法为:
y n = ( x ∗ w ) [ n ] = ∑ k = 1 ∣ w ∣ x n + k − 1 w k = w T x n : n + ∣ w ∣ − 1 y_n=(x*\boldsymbol{w})[n]=\sum_{k=1}^{|\boldsymbol{w}|}x_{n+k-1}w_k=w^{\mathsf{T}}x_{n:n+|w|-1} yn=(x∗w)[n]=k=1∑∣w∣xn+k−1wk=wTxn:n+∣w∣−1
y 中的元素与 x 中的元素有如下导数关系:
∂ y n − k + 1 ∂ x n = w k , ∂ y n ∂ w k = x n + k − 1 , f o r 1 ≤ k ≤ ∣ w ∣ \frac{\partial y_{n-k+1}}{\partial x_n}=w_k,\quad\frac{\partial y_n}{\partial w_k}=x_{n+k-1},\quad\mathrm{for}1\leq k\leq|w| ∂xn∂yn−k+1=wk,∂wk∂yn=xn+k−1,for1≤k≤∣w∣
进⼀步可以得到 J 关于 w 和 x 的导数:
δ n ( x ) = ∂ J ∂ y ∂ y ∂ x n = ∑ k = 1 ∣ w ∣ ∂ J ∂ y n − k + 1 ∂ y n − k + 1 ∂ x n = ∑ k = 1 ∣ w ∣ δ n − k + 1 ( y ) w k = ( δ ( y ) ∗ f l i p ( w ) ) [ n ] δ ( x ) = δ ( y ) ∗ f l i p ( w ) ∂ ∂ w k J = ∂ J ∂ y ∂ y ∂ w k = ∑ n = 1 ∣ y ∣ ∂ J ∂ y n ∂ y n ∂ w k = ∑ n = 1 ∣ y ∣ δ n ( y ) x n + k − 1 = ( δ ( y ) ∗ x ) [ k ] ∂ ∂ w J = δ ( y ) ∗ x \begin{aligned} \delta_{n}^{(\boldsymbol{x})}=\frac{\partial J}{\partial\boldsymbol{y}}\frac{\partial\boldsymbol{y}}{\partial x_{n}}& =\sum_{k=1}^{|\boldsymbol{w}|}\frac{\partial J}{\partial y_{n-k+1}}\frac{\partial y_{n-k+1}}{\partial x_{n}}=\sum_{k=1}^{|\boldsymbol{w}|}\delta_{n-k+1}^{(\boldsymbol{y})}w_{k}=(\delta^{(\boldsymbol{y})}*\mathrm{flip}(\boldsymbol{w}))[n] \\ \delta^{(x)}& =\delta^{(\boldsymbol{y})}*\mathrm{flip}(\boldsymbol{w}) \\ \begin{aligned}\frac{\partial}{\partial w_{k}}J=\frac{\partial J}{\partial\boldsymbol{y}}\frac{\partial\boldsymbol{y}}{\partial w_{k}}\end{aligned}& =\sum_{n=1}^{|y|}\frac{\partial J}{\partial y_{n}}\frac{\partial y_{n}}{\partial w_{k}}=\sum_{n=1}^{|y|}\delta_{n}^{(y)}x_{n+k-1}=(\delta^{(y)}*x)[k] \\ \frac\partial{\partial\boldsymbol{w}}J& =\delta^{(\boldsymbol{y})}*\boldsymbol{x} \end{aligned} δn(x)=∂y∂J∂xn∂yδ(x)∂wk∂J=∂y∂J∂wk∂y∂w∂J=k=1∑∣w∣∂yn−k+1∂J∂xn∂yn−k+1=k=1∑∣w∣δn−k+1(y)wk=(δ(y)∗flip(w))[n]=δ(y)∗flip(w)=n=1∑∣y∣∂yn∂J∂wk∂yn=n=1∑∣y∣δn(y)xn+k−1=(δ(y)∗x)[k]=δ(y)∗x
⾄此,我们拆解了卷积核作⽤在输⼊上的导数与反向传播过程。映射到⼆维卷积,这也是得到了⼀个⼆维卷积核作⽤在⼆维输⼊数组上的结论。推导⼆维卷积的导数与反向传播的过程类似
多通道
在实际的卷积核中,我们还需要考虑通道。上⽂介绍的多通道输⼊,后⼀层的每个通道都是由前⼀层的各个通道经过卷积再求和得到的。我们将这个过程可以理解为全连接,节点为⼀个通道的输⼊数组
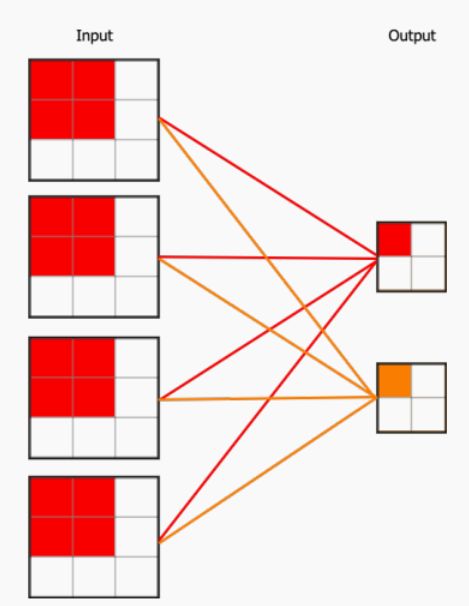
考虑多通道下的卷积运算。输⼊的每个通道先与不同卷积核组相应的卷积核运算,再累加得到输出的对应位置。这个过程可以视作全连接,将单个卷积核视作权重
使⽤ GEMM 转换
单层池化层
池化的导数及后向传播
池化函数是⼀个下采样函数,对于⼤⼩为 m 的池化区域,池化函数及其导数可以定义为:
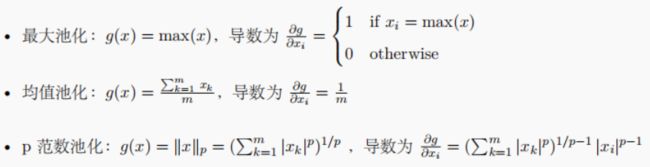
下采样的后向传播过程为上采样,其⽰意图为:
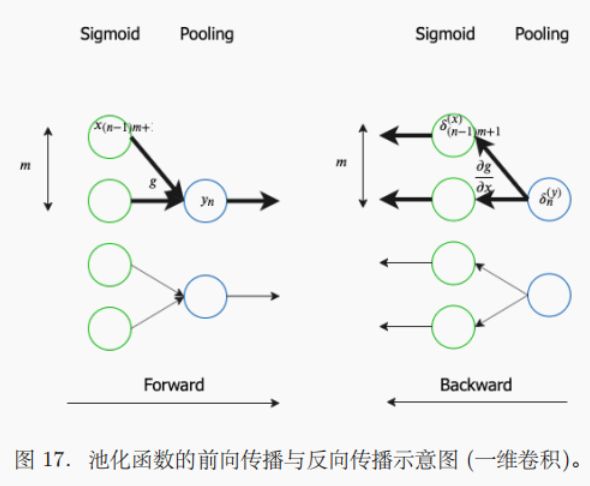
该后向传播过程就是利⽤ g 的导数将误差信号传递到 g 的输⼊
δ ( n − 1 ) m + 1 : n m ( x ) = ∂ ∂ x ( n − 1 ) m + 1 : n m J = ∂ J ∂ y n ∂ y n ∂ x ( n − 1 ) m + 1 : n m = δ n ( y ) g n ′ δ ( x ) = u p s a m p l e ( δ ( y ) , g ′ ) \begin{aligned} \delta_{(n-1)m+1:nm}^{(x)}=\frac{\partial}{\partial x_{(n-1)m+1:nm}}J& =\frac{\partial J}{\partial y_{n}}\frac{\partial y_{n}}{\partial x_{(n-1)m+1:nm}}=\delta_{n}^{(\boldsymbol{y})}g_{n}^{\prime} \\ \delta^{(x)}& =upsample(\delta^{(\boldsymbol{y})},g^{\prime}) \end{aligned} δ(n−1)m+1:nm(x)=∂x(n−1)m+1:nm∂Jδ(x)=∂yn∂J∂x(n−1)m+1:nm∂yn=δn(y)gn′=upsample(δ(y),g′)
上采样
上采样 (upsampling) 具体展⽰如下,假设池化⼤⼩为 2*,* 2,步幅为 2,且 δ ( y ) \delta^{(\boldsymbol{y})} δ(y)第 k 个⼦矩阵为:
δ k ( y ) = ( 2 4 6 8 ) \delta_k^{(y)}=\left(\begin{array}{cc}2&4\\6&8\end{array}\right) δk(y)=(2648)
先将 δ k ( y ) \delta_k^{(\boldsymbol{y})} δk(y)还原成:
( 0 0 0 0 0 2 4 0 0 6 8 0 0 0 0 0 ) \left(\begin{array}{ccccc}0&0&0&0\\0&2&4&0\\0&6&8&0\\0&0&0&0\end{array}\right) 0000026004800000
如果是最⼤池化,假设之前在前向传播时记录的最⼤值位置分别是左上,右上,左下,右下,则转换后的矩阵为:
( 2 0 0 4 0 0 0 0 0 0 0 0 6 0 0 8 ) \left(\begin{array}{cccc}2&0&0&4\\0&0&0&0\\0&0&0&0\\6&0&0&8\end{array}\right) 2006000000004008
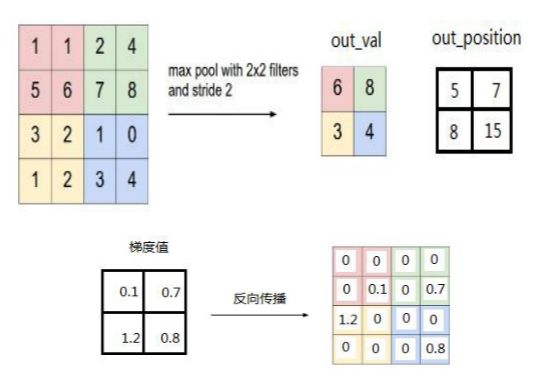
如果是均值池化,根据公式可以得到:
( 0.5 0.5 1.0 1.0 0.5 0.5 1.0 1.0 1.5 1.5 2.0 2.0 1.5. 1.5 2.0 2.0 ) \left(\begin{array}{cccc}0.5&0.5&1.0&1.0\\0.5&0.5&1.0&1.0\\1.5&1.5&2.0&2.0\\1.5.&1.5&2.0&2.0\end{array}\right) 0.50.51.51.5.0.50.51.51.51.01.02.02.01.01.02.02.0
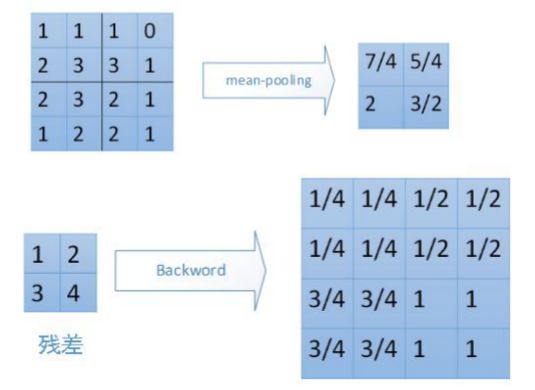
数据增强
跳转到参考链接
数据增强(Data augmentation)
为了要保证完美地完成项目,有两件事情需要做好:
- 寻找更多的数据
- 数据增强
增加训练数据,则能够提升算法的准确率,因为这样可以避免过拟合,而避免了过拟合你就可以增大你的网络结构了。当训练数据有限的时候,可以通过一些变换来从已有的训练数据集中生成一些新的数据
翻转(Flip)
可以对图片进行水平和垂直翻转。一些框架不提供垂直翻转功能。但是,一个垂直反转的图片等同于图片的180度旋转,然后再执行水平翻转。下面是我们的图片翻转的例子

随机裁剪(crop采样)
与缩放不同,我们只是从原始图像中随机抽样一个部分。然后,我们将此部分的大小调整为原始图像大小。这种方法通常称为随机裁剪。以下是随机裁剪的示例

fancy PCA
其中[P1,P2,P3]表示特征向量,[λ1,λ2,λ3]表示特征值。在论文中α是一个服从均值为0,标准差为0.1的高斯分布。对于同一张图像,α = α1 = α2 = α3。上述公式得到的结果是一个尺寸为(3, 1)的向量,原图像的每个像素(R, G, B)都加上这个向量得到新的目标图像
[ p 1 , p 2 , p 3 ] [ α 1 λ 1 , α 2 λ 2 , α 3 λ 3 ] T [\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3][\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3]^T [p1,p2,p3][α1λ1,α2λ2,α3λ3]T
- 像素值归一化
- 将归一化的图像转化成三维向量
- 求协方差矩阵
- 求出特征值与特征向量
- 对特征值从大到小进行排序,并使特征向量与对应特征值的位置保持一致
- 将特征向量[P1, P2, P3]与公式中[α1λ1, α2λ2, α3λ3]相乘
- 将add_vect加到原图像的每一个像素
样本不均衡
增加小众类别的图像数据

其余数据增强方式
- 平移变换
- 旋转/仿射变换
- 高斯噪声、模糊处理
- 对颜色的数据增强:图像亮度、饱和度、对比度变化
训练和测试间的协调
- 训练阶段常用数据增强,而测试阶段少用。但训练末期移除数据增强,再传统测试,可略增性能
- 若训练时持续使用尺度和长宽比的增强,测试时采取相同策略,如随机选取32个裁剪图片测试,能进一步提升性能
- 训练中,设定固定尺度,每个epoch内随机选尺度。测试中,生成多尺度feature map,为每个Region Proposal在不同尺度上选择最合适的尺寸
- **总结:**多尺度训练与多尺度测试可提高模型性能
超参数的调节
跳转到参考链接
超参数是我们控制我们模型结构、功能、效率等的调节旋钮
学习率(Learning Rate)
学习率被定义为每次迭代中成本函数中最小化的量。也即下降到成本函数的最小值的速率是学习率,它是可变的。从梯度下降算法的角度来说,通过选择合适的学习率,可以使梯度下降法得到更好的性能

调整策略:
- 固定学习率:为整个训练过程设置一个恒定的学习率。这是最简单的策略,但可能不是最优的
- 学习率衰减:随着训练进度,逐渐降低学习率
- 固定步骤衰减:在预先确定的epoch数减少学习率
- 指数衰减:学习率按指数逐渐减小
- 多项式衰减:学习率按多项式逐渐减小至最小值
- 自适应学习率方法:
- Adagrad:考虑过去所有的梯度
- RMSprop:只考虑过去某一窗口的梯度
- Adam:结合了Momentum和RMSprop的思想
batch_size选择
batch_size的选择会影响模型的训练速度、性能和收敛稳定性在小样本数的数据库中,不使用Batch Size是可行的,而且效果也很好。但是一旦是大型的数据库,一次性把所有数据输进网络,肯定会引起内存的爆炸
Batch Normalization Layer,防止过拟合
Batch Size从小到大的变化对网络影响:
- 没有Batch Size,梯度准确,只适用于小样本数据库
- Batch Size=1,梯度变来变去,非常不准确,网络很难收敛
- Batch Size增大,梯度变准确
- Batch Size增大,梯度已经非常准确,再增加Batch Size也没有用
**注意:**Batch Size增大了,要到达相同的准确度,必须要增大epoch
- **GD(Gradient Descent):**就是没有利用Batch Size,用基于整个数据库得到梯度,梯度准确,但数据量大时,计算非常耗时,同时神经网络常是非凸的,网络最终可能收敛到初始点附近的局部最优点
- **SGD(Stochastic Gradient Descent):**就是Batch Size=1,每次计算一个样本,梯度不准确,所以学习率要降低
- **mini-batch SGD:**就是选着合适Batch Size的SGD算法,mini-batch利用噪声梯度,一定程度上缓解了GD算法直接掉进初始点附近的局部最优值。同时梯度准确了,学习率要加大
其余超参数
变量初始化
常见的变量初始化有随机初始化、均匀分布初始值、正态分布初始值等
训练轮数
模型收敛即可停止迭代,一般可采用验证集作为停止迭代的条件。如果连续几轮模型损失都没有相应减少,则停止迭代
- 激活函数
- 采用sigmoid激活函数计算量较大,而且sigmoid饱和区变换缓慢,求导趋近于0,导致梯度消失。sigmoid函数的输出值恒大于0,这会导致模型训练的收敛速度变慢
- tanh它解决了zero-centered的输出问题,然而,gradient vanishing的问题和幂运算的问题仍然存在
- 正则化
为了防止过拟合,可通过加入l1、l2正则化。从公式可以看出,加入l1正则化的目的是为了加强权值的稀疏性,让更多值接近于零。而l2正则化则是为了减小每次权重的调整幅度,避免模型训练过程中出现较大抖动
- dropout
数据第一次跑模型的时候可以不加dropout,后期调优的时候dropout用于防止过拟合有比较明显的效果,特别是数据量相对较小的时候
- 特征抽取(池化)
max-pooling、avg-pooling是深度学习中最常用的特征抽取方式。max-pooling是抽取最大的信息向量,然而当存在多个有用的信息向量时,这样的操作会丢失大量有用的信息
误差
**过拟合:**过拟合就是模型把数据学习的太彻底,以至于把噪声数据的特征也学习到了,这样就会导致在后期测试的时候不能够很好地识别数据,即不能正确的分类,模型泛化能力太差
**欠拟合:**欠拟合模型没有很好地捕捉到数据特征,不能够很好地拟合数据
误差的变化:
卷积神经网络典型CNN
简介
LeNet-5:
- 最早用于数字识别的CNN
- 卷积层的引入;池化层的使用;非线性激活函数
- 奠定了深度网络的基本结构,卷积加池化,卷积和池化后使用激活函数,softmax函数将输出转化为概率分布
问题:深度限制,可能导致特征提取不够深入;参数效率;限制的可扩展性,输入图像的大小固定
AlexNet:
- **深度优势:**拥有8个卷积层和3个全连接层,使得模型更深入地挖掘图像特征
- **大感受野:**使用11x11、5x5卷积核和3x3池化,捕获更广的图像信息
- **ReLU革命:**替代传统Sigmoid,避免梯度消失,加快训练
- **防过拟合:**全连接层采用Dropout,强化模型泛化
- **并行:**利用GPU并行计算加速进程
问题:模型太大;效率问题;局部连接,这使得模型只能在两个 GPU 上进行并行化训练,限制了扩展性
[ZF Net:](#ZF Net)
- 更小的卷积核:ZF Net将AlexNet中的11x11和5x5的卷积核替换为7x7和3x3的卷积核。这样的设计可以减少参数数量,降低计算复杂度,并且能够更好地捕捉图像的局部特征
- 更深的网络结构:ZF Net在AlexNet的基础上增加了一些卷积层,使得网络更深。深层网络可以更好地学习到图像的抽象特征,提高模型的表达能力和分类性能
- 更小的步长和更大的填充:ZF Net将卷积层的步长从AlexNet的4调整为2,这样可以减小特征图的尺寸,提高特征的空间分辨率。此外,ZF Net还增加了更大的填充,使得特征图的尺寸保持不变,避免信息的丢失
- 反卷积网络和可视化:ZF Net引入了反卷积网络(Deconvolutional Network)来可视化网络学习到的特征。通过反卷积网络,可以将特征图逆向映射回输入图像空间,从而观察到网络在不同层次学习到的特征
- **预训练和微调:**ZF Net使用了与AlexNet相似的训练策略,先在大规模的图像数据集上进行无监督预训练,然后在目标任务上进行有监督微调。这种训练策略可以加快网络的收敛速度,提高模型的泛化能力
问题:复杂性;过度依赖数据,小样本不佳;非根本性的创新,只是微调
VGGNet:
- 深度关键:VGGNet 证明了网络的深度对于模型性能至关重要。它通过将层数增加到16(VGG16)或19层(VGG19)来提高性能,可以更好地学习到图像的高层次特征,提高模型的表达能力和分类性能
- **更小的卷积核:**VGGNet中所有的卷积层都采用3x3的卷积核,这样可以减少参数数量,降低计算复杂度,并且能够更好地捕捉图像的局部特征
- **均一化的网络结构:**VGGNet 明确了通过重复使用简单的3x3卷积核来构建深度网络的有效性。这种均一化设计不仅使网络结构更清晰,也简化了超参数的选择过程
- **更多的卷积层:**VGGNet采用了较多的卷积层,并且每两个卷积层之间都加入了一个池化层。这样可以逐步减小特征图的尺寸,提高特征的空间分辨率,并且可以增加网络的非线性能力
- 小尺寸的全连接层:VGGNet中的全连接层都采用了较小的尺寸,如4096或1024,以减少参数数量和计算复杂度。此外,VGGNet还采用了Dropout正则化技术来减少过拟合的风险
- **预训练和微调:**VGGNet同样使用了与AlexNet和ZF Net相似的训练策略,先在大规模的图像数据集上进行无监督预训练,然后在目标任务上进行有监督微调。这种训练策略可以加快网络的收敛速度,提高模型的泛化能力
问题:参数数量太大;过拟合,小数量样本
GoogLeNet:
- Inception结构:GoogLeNet采用了一种称为Inception结构的模块化设计。这种结构通过并行使用多个不同尺寸的卷积核和池化操作,从而在不同尺度上捕捉图像的特征。Inception结构可以在不增加网络深度和参数数量的情况下,提高网络的表达能力和特征提取能力
- 1x1卷积核的使用:GoogLeNet中广泛使用了1x1的卷积核。1x1卷积核可以在不改变特征图尺寸的情况下,对特征进行降维或升维操作。通过1x1卷积核,可以减少特征图的通道数,降低计算复杂度,并且可以引入非线性变换,增加网络的表达能力
- 辅助分类器:为了缓解梯度消失问题和提高网络的训练效果,GoogLeNet引入了辅助分类器。在网络的中间层添加了额外的分类器,用于辅助训练,同时也可以提供更多的梯度信号,加速网络的收敛速度
- **无全连接层,平均池化:**GoogLeNet采用了全局平均池化层来代替全连接层。全局平均池化可以将特征图的每个通道的特征进行平均,得到一个固定长度的特征向量。这样可以大大减少参数数量,并且可以提高网络的泛化能力
问题:参数数量太大;超参数调优
ResNet:
- 残差连接:ResNet引入了残差连接(residual connection)的概念,即通过跳跃连接将输入直接添加到输出中。这样可以使得网络能够学习到残差(residual)部分,即输入与输出之间的差异,而不是直接学习输入与输出之间的映射。残差连接可以有效地解决梯度消失和梯度爆炸问题,使得网络更容易训练,并且可以支持更深的网络结构
- 堆叠的残差块:ResNet将网络组织为多个堆叠的残差块(residual block)。每个残差块由多个卷积层组成,其中包括一个主要的卷积层和若干个附加的卷积层。这样的设计可以增加网络的深度,并且每个残差块内部的卷积层可以共享参数,减少了网络的参数数量
- 恒等映射和投影映射:为了保持输入和输出的维度一致,ResNet引入恒等映射(identity mapping)和投影映射(projection mapping)。恒等映射通过跳跃连接直接将输入添加到输出中,不改变维度;而投影映射则使用1x1的卷积层来改变维度,使得输入和输出的维度一致。这样可以使得网络更加灵活,适应不同的输入和输出维度
- **全局平均池化和全连接层:**与之前的网络模型类似,ResNet也采用了全局平均池化层来代替全连接层。全局平均池化可以将特征图的每个通道的特征进行平均,得到一个固定长度的特征向量。这样可以大大减少参数数量,并且可以提高网络的泛化能力
问题:参数数量太大;计算成本大
DenseNet:
- 密集连接:DenseNet引入了密集连接(dense connection)的概念,即将每个卷积层的输出直接连接到所有后续的卷积层的输入上。这样可以使得网络更加紧密地连接在一起,每个卷积层可以直接利用前面所有层的特征信息,从而提高了特征的重用性和信息的流动性
- **特征复用:**由于每一层都可以访问前面层的特征,DenseNet极大地提高了特征的复用,使网络即使在较少的参数下也能表达强大的功能
- **参数效率:**DenseNet具有高度的参数效率,这意味着即使在较少的参数情况下,它也能达到与其他深层网络相似的性能
- **瓶颈层:**DenseNet中使用了瓶颈层(bottleneck layer)的设计,即先使用1x1的卷积层将输入的通道数减少,然后再使用3x3的卷积层进行特征提取,最后再使用1x1的卷积层将通道数恢复。这样可以减少计算量和参数数量,同时也可以提高网络的表达能力
- **稠密块:**DenseNet将网络组织为多个稠密块(dense block)。每个稠密块由多个瓶颈层组成,其中包括一个主要的瓶颈层和若干个附加的瓶颈层。这样的设计可以增加网络的深度,并且每个稠密块内部的瓶颈层可以共享参数,减少了网络的参数数量
- **过渡层:**为了减少特征图的尺寸和通道数,DenseNet引入了过渡层(transition layer)。过渡层包括一个1x1的卷积层和一个2x2的平均池化层,可以将特征图的尺寸减半,同时也可以将通道数减少。这样可以使得网络更加轻量化,减少计算量和参数数量
问题:计算复杂性增加;显存占用,由于需要保存所有中间层的输出特征以供后续层使用
SeNet:
- 通道注意力机制:SENet提出了一个简单但有效的模块,即压缩和激励(Squeeze-and-Excitation)模块,来显式地建模卷积特征的通道间依赖关系。这允许模型为每个通道分配适当的权重,从而加强那些更有意义的特征
- Squeeze操作:SENet中的Squeeze操作是指将特征图的通道维度进行压缩。具体来说,Squeeze操作使用全局平均池化层将特征图的空间维度降为一个数值,然后再通过一个全连接层将其映射到一个较小的数值。这样可以减少计算量和参数数量,并且可以提取通道维度上的全局信息
- Excitation操作:SENet中的Excitation操作是指根据Squeeze操作得到的权重,对特征图的通道维度进行重新加权。具体来说,Excitation操作使用一个sigmoid函数将Squeeze操作得到的权重映射到0到1之间的范围,然后将其与原始特征图相乘,得到加权后的特征图。这样可以使得网络更加关注重要的通道,抑制不重要的通道,提高特征的表达能力
- **参数与计算效率:**SE模块增加的参数和计算开销相对较小,但能显著提高模型的性能。这意味着只需微小的代价,就可以提高网络的表示能力。
- **兼容性:**SE模块具有高度的灵活性和通用性,可以与现有的许多主流网络结构(如ResNet、DenseNet等)结合,进一步提高它们的性能
问题:计算开销大;过拟合风险;权衡选择,性能提升与计算效率
MobileNet:
V1:
- **轻量级与效率:**MobileNet旨在为移动和嵌入式设备提供高效的深度学习模型,它在维持相对较高性能的同时,大大降低了模型的大小和计算量
- 深度可分离卷积包括深度卷积和逐点卷积,深度卷积只处理通道维度,逐点卷积只处理空间维度。这样可以显著减少计算量和参数数量,同时也可以提高网络的效率和准确率
- **超参数调节:**MobileNet引入了两个重要的超参数,宽度乘子和分辨率乘子,允许开发者根据具体的资源限制和性能需求对网络进行微调
V2:
- 线性瓶颈 (Linear Bottlenecks): MobileNetV2 引入了一个新的特征,称为线性瓶颈。这意味着在瓶颈层之后,模型不使用任何非线性激活函数,从而降低了模型复杂性并提高了效率
在常规的卷积神经网络中,每一个卷积层后通常都会跟随一个非线性激活函数。这些非线性激活函数能够帮助网络捕获复杂的特征和模式。然而,过度的非线性处理可能会导致信息损失,特别是当对特征图进行通道压缩时
MobileNetV2 通过引入逆残差块(inverted residual blocks)与线性瓶颈的组合来处理这个问题。在逆残差块中:
- 扩展层:首先使用 1x1 的卷积增加通道数(扩展特征图的维度)
- 深度卷积层:接着进行一个 3x3 的深度卷积操作
- 线性瓶颈:然后再次使用 1x1 的卷积压缩通道数,但这次没有后续的非线性激活函数
线性瓶颈的关键思想是在最后的 1x1 卷积(压缩阶段)后不使用非线性激活。这意味着输出保持为线性,从而减少了潜在的信息损失。这种设计方式使得网络可以在减少计算成本的同时,仍然能够有效地捕获和保留关键信息
- 逆残差结构 (Inverted Residuals): 与常规残差块相反,MobileNetV2 首先使用 1x1 卷积来扩展通道数,然后通过 3x3 的深度分离卷积进行处理,最后再通过 1x1 卷积压缩通道数。这种设计减少了计算和参数数量,同时保持了网络的表现力
V3:
- 神经架构搜索(NAS): MobileNetV3是基于硬件感知的神经架构搜索来优化的。这使得它可以为特定的硬件平台找到最佳的模型架构,提高效率和性能
- 新的激活函数 - h-swish:与MobileNetV2的ReLU6相比,V3采用了新的激活函数h-swish,这有助于模型在保持轻量级的同时获得更好的性能
问题:在某些硬件上,实际的速度提升可能没有理论上那么显著;尽管性能有所提高,但与某些大型架构(如ResNet)相比,仍有差距;NAS带来的结构可能过于复杂,不易于理解或解释;为优化性能可能需要特定的硬件特性或软件实现
ShuffleNet:
通道打乱 (Channel Shuffle):通过重新排列通道来允许跨组的信息流通,确保组卷积后的每个通道都获得了来自输入的不同通道的信息
点群卷积 (Pointwise Group Convolution):不是全连接地进行1x1卷积,而是在通道上进行分组,从而减少计算量
高效网络架构设计的几个实用指南
LeNet-5
结构与重要讨论
LeNet-5是由Yann LeCun等人
跳转到参考链接
视频-LeNet-5论文关键点解读
视频-手搓代码复原
LeNet-5网络结构:
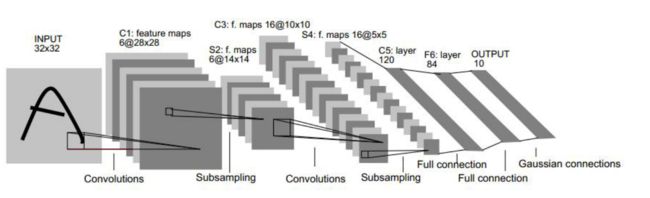
- LeNet-5简介:LeNet-5 是一个典型的字符识别卷积网络,处理的输入图像都已被规范化。
- 局部连接与初级特征提取:局部连接在视觉学习中常用,它通过局部感受野帮助神经元提取视觉特征,如边缘和角点。
- 权值共享与特征位置:特征位置会随输入变化,但通过权值共享,局部特征检测器可应用于整张图像。
- 特征图与多重特征:神经元的输出称为特征图,完整的卷积层有多个这样的特征图,因此在每个位置可以形成多重特征。
- LeNet输入和感受野:LeNet的首层有6张特征图,特征图中的神经元计算基于5x5的感受野。
- 权重共享与局部特征:在一个特征图内,所有神经元使用相同的权重和偏置,确保识别图像中的相似局部特征。
- 卷积网络的命名:LeNet中的特征图生成等同于卷积操作,因此得名“卷积网络”。
- 卷积核定义:卷积核即特征图中神经元使用的权重集合。
- CNN的鲁棒性:输入图像的平移会导致特征图的同样平移,保证CNN对位置和形状变化的鲁棒性。
- 下采样层的特性:下采样层通过局部平均降低特征图分辨率,减少对平移、形变的敏感度。
- 下采样的后续处理:经过下采样后,特征图的大小减半。而可训练的参数和偏置则决定了其非线性表现。
- 金字塔架构与几何变换不变性:卷积层和下采样层交替连接,形成“金字塔”结构,确保了特征图分辨率逐渐降低而数量逐渐增加,增强了对几何变换的鲁棒性
LeNet-5全流程详解

在接下来的叙述中,卷积层标记为Cx,下采样层标记为Sx,全连接层标记为Fx,其中x代表第几层
- 输入层
总层数: 7层 (不包括输入层)
- 输入: 32x32像素的图像,比MNIST的最大尺寸(28x28)大
- 目的: 使得特征(如笔画端点、角点)出现在特征检测器感受野的中心
- 感受野中心: 在32x32输入图像中为20x20区域(对于C3层)
- 像素标准化: 背景(白色)为-0.1,前景(黑色)为1.175,使输入平均值为0,方差为1,从而加速训练
结论: LeNet-5通过使用大于MNIST标准尺寸的输入和特定的像素标准化策略,旨在有效地提取图像中的关键特征并加速训练
C1 (第一卷积层)
- 类型: 卷积层
- 特征图数量: 6张
- 特征图大小: 28x28,基于5x5的卷积核
- 参数: 156个可训练参数
- 连接: 122,304个
结论: C1层使用5x5的卷积核为每张图生成28x28大小的特征图,共有6张,含有156个参数和122,304个连接
S2 (第一下采样层)
- 类型: 下采样层
- 特征图数量: 6张
- 特征图大小: 14x14,基于2x2非重叠的感受野
- 计算方式: 取平均 → 乘系数 → 加偏置 → sigmoid函数
- 参数: 12个可训练参数
- 连接: 5880个
结论: S2层对C1层的输出进行下采样,生成6张14x14的特征图。每个神经元采用2x2的非重叠区域,并通过sigmoid激活函数进行计算。共有12个参数和5880个连接
C3 (第二卷积层)
- 类型: 卷积层
- 特征图数量: 16张
- 连接方式
- 并非一对一连接S2和C3特征图
- C3前6张通过S2的3张特征图计算
- 接下来的6张通过S2的4张特征图计算
- 接下来的3张通过S2的非连续4张特征图计算
- 最后一张连接所有S2特征图
- 原因
- 减少连接数,维持合理范围
- 打破网络对称性,提取不同输入特征
- 参数: 1516个可训练参数
- 连接: 151600个
结论: C3层有16张特征图,与S2层非一对一连接。该层设计为打破对称性,从S2的不同特征图集合中提取特征,包含1516个参数和151600个连接
S4 (第二下采样层)
- 类型: 下采样层
- 特征图数量: 16张
- 特征图大小: 5x5
- 参数: 32个可训练参数
- 连接: 2000个
结论: S4层有16张5x5大小的特征图,每个神经元与C3的2x2邻域相对应。该层有32个参数和2000个连接
C5 (第三卷积层)
- 类型: 卷积层
- 特征图数量: 120张
- 特征图大小: 1x1
- 连接: 48,120个
结论: C5层由120张1x1的特征图组成,每个神经元与S4层的16张5x5特征图全连接。尽管特征图为1x1,但在LeNet-5的输入增大时,其尺寸会变化。此层有48,120个可训练连接
F6 (全连接层)
- 类型: 全连接层
- 神经元数量: 84个
- 连接: 10,164个可训练参数
结论: F6层有84个神经元,与C5层全连接,包含10,164个可训练参数。选择84作为神经元数目是为了体现ASCII字符标准的7x12大小位图上每个像素点的特性
输出层
- 类型: 输出层
- 单元类型: 欧式径向基函数 (RBF)
- 单元数量: 按类别分,每类一个单元
- 每个单元的输入数量: 84个
结论: 输出层采用欧式径向基函数(RBF)单元,每个类别对应一个单元。每个RBF单元有84个输入
LeNet论文
LeNet-5,由Yann LeCun于1990年代中期提出,是早期卷积神经网络的代表之一,专为手写数字识别设计。回顾LeNet的论文,有一些关键的观点和挑战值得注意:
- 历史背景:首先,考虑到LeNet是在1990年代中期提出的,那时的计算能力、数据量和深度学习的理论都与今天大相径庭。因此,当我们评估LeNet的设计和决策时,需要考虑到当时的技术和理论背景
- 激活函数:LeNet使用sigmoid或tanh作为其激活函数,而不是现代网络中更常用的ReLU。这可能限制了网络的训练速度和性能
- 权重共享:LeNet-5是早期使用权重共享策略的网络,这是现代卷积网络的基石。然而,权重共享在当时是一种新颖的概念,论文中可能不会像现代文献那样详细解释它
- 不使用偏置项:在某些层,LeNet-5没有使用偏置项。这与现代的CNN设计有所不同,因为现在偏置项被广泛认为是网络设计中的一个重要组成部分
- 平均池化:LeNet使用了平均池化而不是现在更流行的最大池化。虽然两者都有其优点,但最大池化在许多现代应用中已被证明效果更佳
- 学习策略:LeNet的训练策略与现代的策略有所不同。例如,它使用了更早期的随机梯度下降方法,没有动量或其他现代优化技巧
- 应用范围:LeNet主要用于手写数字识别(基于MNIST数据集)。这限制了它处理更复杂任务或大型图像数据集的能力
- 模型规模:与现代的深度CNN(如VGG,ResNet等)相比,LeNet的规模相对较小。它只有几个卷积层和全连接层
- 文档可读性:由于LeNet是在深度学习还处于起步阶段的时候提出的,它的文档和描述方式可能不如现代的文献那么直观或详细
AlexNet
AlexNet结构
Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton
跳转到参考链接
视频-AlexNet论文关键点解读
视频-论文详细
AlexNet网络结构:
局部响应归一化(Local response normalization,LRN)
LRN通过在相邻卷积核生成的feature map之间引入竞争,从而有些本来在feature map中显著的特征在A中更显著,而在相邻的其他feature map中被抑制,这样让不同卷积核产生的feature map之间的相关性变小
局部响应归一化(Local Response Normalization,LRN)是一种在深度学习,特别是在卷积神经网(CNN)中使用的正则化技术。它的核心目的是为了增强模型的泛化能力,具体方法和思想可以从以下几点来理解:
- 竞争性激活:在神经生物学中,一个活跃的神经元能够抑制其附近的其他神经元的激活,确保只有反应最强的神经元能够传达信号。这种概念被称为"侧抑制"或"竞争性激活"。LRN正是模拟这一现象,通过对局部神经元的活动建立竞争机制,使得较大的响应值相对变得更大,而抑制响应小的神经元
- 特征显著性:LRN可以确保某一特征在一个feature map中显著的情况下,在相邻的feature map中被抑制。这样,不同卷积核产生的feature map之间的相关性减小。这意味着模型更加关注于特定的、显著的特征,并减少其他不显著的特征的影响
- 增强泛化能力:因为LRN减少了不同feature map之间的相关性,这使得模型更容易找到真正有意义的、区分性的特征。因此,模型对于新的、未见过的数据有更好的预测能力
综上,局部响应归一化(LRN)是一种模仿生物神经机制的正则化策略,在某些深度学习模型中能有效地增强泛化能力和突显关键特征
AlexNet创新点
成功使用ReLU作为CNN的激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题。ReLU可以有效地解决梯度消失问题,并且在训练过程中可以加速收敛。此外,ReLU还可以提高模型的稀疏性,减少过拟合的风险
在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖,提升了特征的丰富性
GPU实现:在每个GPU中放置一半核(或神经元),还有一个额外的技巧:GPU间的通讯只在某些层进行
防止过拟合:
训练时使用Dropout随机忽略一部分神经元,以避免模型过拟合。Dropout虽有单独的论文论述,但是AlexNet将其实用化,通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。在全连接层的前两层中使用了 Dropout方法按一定比例随机失活神经元,以减少过拟合。后来,发现Dropout并不是模型融合,而是正则项
数据增强(Data augmentation)
- 数据扩充方法**:平移、水平翻转、裁剪
- 原始图片大小:256x256像素
- 裁剪后的图片大小:224x224像素
- 扩充倍数:2048倍。计算方法是:(256−224)×(256−224)×2(256−224)×(256−224)×2
- 测试策略:从每张图片中提取五个224x224的图(四角和中心),并进行水平翻转,共得到10个图。使用模型对这10个图进行预测,并对预测结果取平均
- 增强效果:使模型适应于只包含图像部分内容的情景(如只有人的一半),提高模型的泛化能力和识别广度
结论:通过裁剪、平移和水平翻转的方法,将256x256的图片转为224x224,实现了数据集的2048倍扩充,进而可以训练更大的网络。测试时采用多图预测策略增强模型的泛化能力。这种数据增强策略可以帮助模型更好地处理不完整的图像内容,如只有人的一半
第二种数据增强的方法就是在图像中每个像素的R、G、B值上分别加上一个数,用到的方法为PC
- 提出了LRN层
- ImageNet的分辨率不一样,论文将图片都裁剪为了[256, 256],没有任何预处理,在raw RGB values of the pixels. 这个点是非常重要的工作,但是论文没有强调
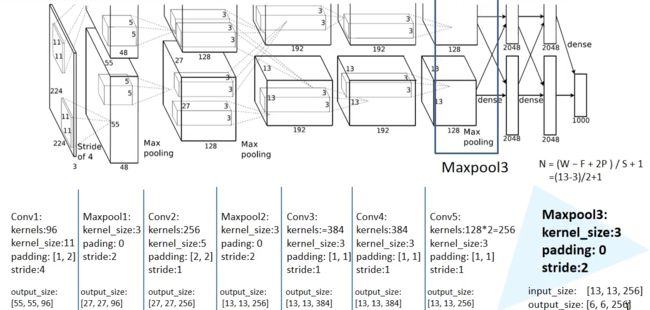
AlexNet全流程详解
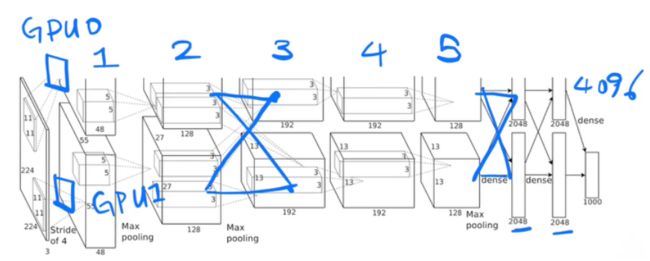
好的,我将详细地描述一张
227x227的彩色图片经过AlexNet网络的整个处理过程
- 输入:
- 大小为
227x227x3的彩色图片。其中,3代表颜色的三个通道:红、绿、蓝- 第一层: 卷积层 + ReLU + 池化:
- 卷积: 使用96个
11x11x3的滤波器(步长为4)进行卷积操作,输出的尺寸为55x55x96- ReLU: 对输出应用ReLU激活函数
- 池化: 使用
3x3的滤波器(步长为2)进行最大池化操作,将输出大小减少为27x27x96- 第二层: 卷积层 + ReLU + 池化:
- 卷积: 使用256个
5x5x48的滤波器进行卷积操作(填充为2)。但是,这里有一个细节:原始的27x27x96输入被分为两组,每组27x27x48,两组在两个不同的GPU上分别进行计算,所以每组的卷积输出是27x27x128。两组的结果再合并,得到完整的27x27x256输出- ReLU: 对输出应用ReLU激活函数
- 池化: 使用
3x3的滤波器(步长为2)进行最大池化操作,输出是13x13x256- 第三层: 卷积层 + ReLU:
- 卷积: 使用384个
3x3x256的滤波器(填充为1)进行卷积操作,输出尺寸为13x13x384- ReLU: 对输出应用ReLU激活函数
- 第四层: 卷积层 + ReLU:
- 卷积: 使用384个
3x3x384的滤波器(填充为1)进行卷积操作,输出尺寸为13x13x384- ReLU: 对输出应用ReLU激活函数
- 第五层: 卷积层 + ReLU + 池化:
- 卷积: 使用256个
3x3x192的滤波器进行卷积操作(填充为1)。与第二层类似,原始的13x13x384输入被分为两组,每组13x13x192。两组在两个不同的GPU上分别进行计算,每组的卷积输出是13x13x128。两组的结果再合并,得到完整的13x13x256输出- ReLU: 对输出应用ReLU激活函数
- 池化: 使用
3x3的滤波器(步长为2)进行最大池化操作,输出是6x6x256- 第六层: 全连接层 + ReLU + Dropout:
- 输入的
6x6x256(即9216个节点)被连接到4096个节点- ReLU激活函数
- Dropout: 为了防止过拟合,进行Dropout操作。
- 第七层: 全连接层 + ReLU + Dropout:
- 输入的4096个节点被连接到另外4096个节点
- ReLU激活函数
- Dropout
- 第八层: 全连接层:
- 输入的4096个节点被连接到1000个节点。这1000个节点对应于ImageNet数据集中的1000个分类
- 使用Softmax函数,将输出转化为每个类别的概率
- 输出:
- 输出是一个1000维的向量,代表输入图片被分为1000个类别中每一个的概率
经过这九步的处理,AlexNet为输入的
227x227的彩色图片产生了一个1000维的概率输出,描述了图片可能属于的每一个类别的概率
训练细节
- 数据增强:
- 为了增加数据量和模型的鲁棒性,AlexNet使用了图像增强技术。包括随机裁剪、水平翻转和颜色变化等
- 输入图像先被调整到
256x256的大小,然后随机裁剪到227x227以用作网络的输入,这增加了模型的空间鲁棒性- 图像的RGB通道值也经过PCA处理,并添加了一定量的噪声,以进一步提高模型对原始图像颜色和亮度变化的鲁棒性
- Dropout:
- 在全连接层,AlexNet引入了Dropout技术来防止过拟合。训练过程中,每次迭代会随机丢弃(将其设置为0)一半的节点
- Dropout仅在训练时使用。在测试或推理时,所有的节点都被使用,并乘以一个固定的概率(例如0.5),以平衡前向传播的活跃节点数量
- ReLU激活函数:
- AlexNet在其卷积层和全连接层中都使用了ReLU (Rectified Linear Unit) 激活函数,它在当时比传统的sigmoid或tanh激活函数更有效。ReLU有助于解决梯度消失问题,并允许更深的网络被有效地训练
- 双GPU训练:
- 由于当时的硬件限制,AlexNet是在两块GTX 580 3GB GPU上进行训练的。网络被分为两部分(如前面提到的分组卷积),每部分在一个GPU上运行
- 局部响应归一化 (Local Response Normalization, LRN):
- 位于ReLU激活函数之后的卷积层采用了LRN。这种归一化方式被认为可以模拟神经生物学中的侧抑制机制,有助于增强模型的泛化能力。但是,在后续的深度学习模型中,LRN的使用逐渐减少,被其他正则化技术所替代
- 权重衰减与动量:
- 使用了L2权重衰减
- 使用了动量来加速SGD的收敛
- 学习率策略:
- 初始学习率设置为0.01,并在训练过程中逐渐降低。当验证错误率不再下降时,学习率被除以10。总体上,学习率在训练过程中减小了三次
- 批次大小与迭代次数:
- 使用了大小为128的批次进行训练
- 模型进行了大约90个epoch的训练
- 优化器:使用SGD进行训练。SGD的内在噪声可以提高模型的泛化性。现今,SGD依然是最主流的优化算法
- 权重衰减:使用了L2 Regularization,这对于模型的泛化非常关键
- 动量:设置为0.9,帮助加速收敛
- 权重初始化:使用均值为0、方差为0.01的高斯随机分布进行初始化。这是一个经验选择,大型模型如BERT则使用了0.02
- 偏移(Bias)初始化:通常初始化为0,但AlexNet的2/4/5的卷积层和全连接层的偏移初始化为1
- 学习率策略:
- 所有层的学习率均设置为0.01
- 当验证误差停止下降时,学习率手动减小10倍
- 主流做法:例如,当训练ResNet的120层时,每30轮学习率减小0.01。或者前60轮保持不变,之后再降低。有的模型选择更平滑的学习率下降策略,如余弦衰减
- 学习率的可视化:AlexNet采用了类似“蓝色”下降策略,而现代的方法可能更倾向于“红色”策略
AlexNet论文
- 双GPU训练:AlexNet使用了两块GPU进行训练,部分因为当时单块GPU的内存无法满足整个网络的需求。这导致模型中有特定的设计(如分组卷积),这在今天的深度学习设计中可能看起来有点奇怪
- 局部响应归一化 (LRN):虽然LRN在AlexNet中被认为是有用的,但在后续的神经网络结构中,LRN的使用减少了,因为它并没有明显的长期效益
- 数据增强:虽然数据增强技术对于模型的性能提升很关键,但论文中关于数据增强的描述不够详细。这可能会给希望复现结果的研究者带来一些困惑
- 手动调整学习率:在论文中,学习率是手动调整的。今天,自适应的学习率调整策略更为普遍
- Dropout位置:Dropout是一个重要的正则化策略,但在AlexNet中,它只被应用在全连接层。在后续的研究中,Dropout也被应用在其他层,具体效果可能因模型而异
- 细节描述可能不足:与今天的深度学习论文相比,AlexNet的论文在某些技术细节上的描述可能不够完备。对于想要完全复现模型的人来说,这可能是一个挑战
- 扩展性:随着时间的推移,我们已经看到了更深、更广泛的网络架构(如VGG, ResNet等)。这些架构往往在性能和准确性上超越AlexNet,尽管AlexNet为这些后续工作奠定了基础
LeNet与AlexNet结构对比
- 网络深度:
- LeNet-5:包含 2 个卷积层,2 个下采样(池化)层和 2 个全连接层,共计 7 层
- AlexNet:包含 5 个卷积层和 3 个全连接层,共计 8 层
- 输入图像大小:
- LeNet-5:32x32 的灰度图像。
- AlexNet:227x227 的彩色图像
- 激活函数:
- LeNet-5:传统的 sigmoid 或者 tanh 函数
- AlexNet:ReLU 函数,这是当时的一个主要创新,因为 ReLU 能够更好地缓解梯度消失问题
- 局部响应归一化(LRN):
- LeNet-5:没有使用 LRN
- AlexNet:使用了 LRN,这可以帮助增加模型的泛化能力。但在后来的模型中,LRN 的使用逐渐被淘汰
- 池化:
- LeNet-5:使用了平均池化
- AlexNet:使用了最大池化
- 正则化:
- LeNet-5:没有明确的 dropout 正则化
- AlexNet:在其全连接层使用了 dropout 来减少过拟合
- 计算复杂度:
- LeNet-5:相对较小,只有约 60,000 的参数
- AlexNet:明显更大,有 60 million 的参数
- 用途与数据集:
- LeNet-5:主要用于 MNIST 手写数字识别
- AlexNet:用于 ImageNet 数据集,这是一个包含 1000 个类别和超过一百万张图像的大规模数据集
- 硬件:
- LeNet-5:在当时的硬件上运行,没有使用 GPU 加速
- AlexNet:一个主要的创新是使用了两块 GPU 进行训练,因为当时的 GPU 内存无法满足单块 GPU 的需求
ZF Net
ZF Net结构
Matthew D. Zeiler和Rob Fergus
跳转到参考链接
视频-ZFNet论文精读
我们常说的深度学习三大马车:
- 更大规模的数据集
- 更强的GPU
- 更好的正则化策略
创新点:很巧妙的可视化网络中间层特征的方法。使用这个技巧就打破了在此之前的卷积操作的黑箱,然后利用它改进之前的网络(比如Alexnet)
神经网络结构描述
输入层
- 功能:接受图像输入
- 输入:一个224x224的彩色图像
卷积层 1 (Conv1)
- 功能:提取低级特征
- 使用96个7x7的滤波器进行卷积操作,步长为2
- 结果:96个110x110的特征图
- 使用ReLU作为激活函数进行非线性变换
- 进行局部响应归一化(LRN)以增强模型的泛化能力
- 使用3x3的最大池化,步长为2,进行特征降维。结果:96个55x55的特征图
卷积层 2 (Conv2)
- 功能:进一步提取特征
- 使用256个5x5的滤波器进行卷积操作,步长为2
- 结果:256个27x27的特征图
- 使用ReLU进行非线性变换
- 再次进行局部响应归一化(LRN)
- 使用3x3的最大池化,步长为2。结果:256个13x13的特征图
卷积层 3 (Conv3)
- 功能:提取更高级的特征
- 使用384个3x3的滤波器进行卷积操作,步长为1
- 结果:384个13x13的特征图
- 使用ReLU进行非线性变换
卷积层 4 (Conv4)
- 功能:继续特征提取
- 使用384个3x3的滤波器进行卷积操作,步长为1
- 结果:384个13x13的特征图
- 使用ReLU进行非线性变换
卷积层 5 (Conv5)
- 功能:最后一层的特征提取
- 使用256个3x3的滤波器进行卷积操作,步长为1
- 结果:256个13x13的特征图
- 使用ReLU进行非线性变换
- 使用3x3的最大池化,步长为2。结果:256个6x6的特征图
全连接层 1 (FC1)
- 功能:进行非线性变换并准备进行分类
- 将特征图展平,得到一个9216维的向量
- 连接到一个有4096个节点的隐藏层
- 使用ReLU进行非线性变换
- 进行Dropout操作,以避免过拟合
全连接层 2 (FC2)
- 功能:进一步为分类做准备
- 连接到另一个有4096个节点的隐藏层
- 使用ReLU进行非线性变换
- 再次进行Dropout操作
输出层 (FC3)
- 功能:进行分类
- 连接到一个有1000个节点的层(对应于ImageNet的1000个类别)
- 使用Softmax函数,得到每个类别的概率
反向操作介绍
首先构造正常的网络,就还是Alexnet那一套,卷积+Relu+池化+随机梯度下降+反向传播,然后进行正常的卷积操作,我们想看某一层的可视化结果,就指定该层的 feature map不为0,其余的全设为0。然后反向传回到输入(不是梯度的那个反向传播)
正常的是 : 卷积 -> Relu -> 池化
回传: 反池化 -> 反Relu -> 反卷积
目的:反卷积网络的目的是将特征图映射回像素空间,从而理解特定特征的空间结构。
工作原理:
- 对于ZFNet中的每一个卷积操作,都可以使用逆卷积操作来“反向”地重建输入。
- 最大池化的逆操作是使用池化操作时的位置来放置特征值,其他位置设置为0。
- 为了重建ReLU激活后的特征,仅仅需要将负值设为0。
- 这些操作确保重建的图像只关注网络中激活的特征。
具体操作:
a. 逆最大池化:在前向最大池化过程中,记录每一个区域内的最大值位置。在反向过程中,将特征值放置到这些记录的位置,其他位置设置为0。
b. 逆ReLU:将所有的负值设为0。
c. 逆卷积:使用相同的权重,但是卷积操作的方向是相反的。实际上,逆卷积是将每一个特征映射回输入空间。
通过连续应用上述逆操作,ZFNet可以从任意中间层的特征图重建出输入图像。这样得到的重建图像会高亮显示激活的特征,从而帮助研究人员理解每一层关注的图像内容
反池化(上采样)
下采样与上采样的定义
缩小图像(或称为下采样(subsampled)或降采样(downsampled))的主要目的有两个:1、使得图像符合显示区域的大小;2、生成对应图像的缩略图
放大图像(或称为上采样(upsampling)或图像插值(interpolating))的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上
反池化就是正常池化的反向操作,在Alex里采用的是最大池化操作。在正常的最大池化中,提取某一个小区域的最大值作为结果,像下面这样:

- 可以发现,在正常操作时,假设现在操作的是红色区域,就是最后一个四方块格子的时候,里面的最大值是0.5
- 当进行反池化操作时,我们只知道 0.5这个最大值,对于其他的 -0.1,-0.2,0.3这三个元素则不可避免的丢失
- 论文中作者使用了一个方法,在正向最大池化操作时,提取出最大值的同时记录了该最大值在原矩阵中的位置,这个操作称为 switches
反向操作回去:
除了最大值之外的其他元素不可避免的丢失,像下面这样:

所以反池化并没有真正意义上的完全还原,只是一种近似而已
反(转置)卷积
正常的卷积操作:
假设我们有一个 4x4 的输入特征图 I 和一个 3x3 的卷积核 K。卷积操作是将 K 在 I 上滑动,每次与对应的 3x3 窗口进行元素乘然后求和,最后得到一个 2x2 的特征图 O*
反卷积操作:
反卷积旨在将一个较小的特征图放大。在上述的例子中,我们现在假设有一个 2x2 的特征图 ′O′,我们想要将其通过反卷积操作放大到 4x4 的尺寸
- 补零:首先,我们在 ′O′ 的每一行和每一列之间插入零,得到一个新的特征图,其尺寸为 3x3。注意,这并不是必要的步骤,但这有助于我们理解反卷积如何工作
- 使用转置的卷积核:然后,我们使用 KT(即原始卷积核 K 的转置)作为我们的新卷积核。与正常的卷积操作一样,我们将新的卷积核在 3x3 的特征图上滑动,并执行元素乘然后求和操作。这样,我们会得到一个 4x4 的特征图 ′I′
所以,简而言之,反卷积可以看作是卷积的一个"反操作",它使用了卷积核的转置并有时会在输入特征图中插入零来放大特征图
- 卷积过程:
蓝色为输入,上面绿色为输出
- 反卷积过程:
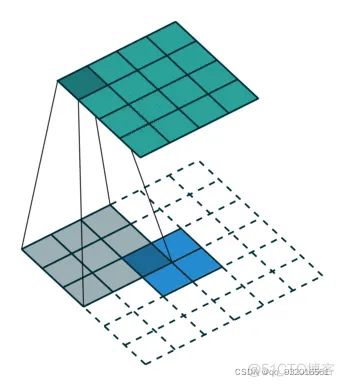
下面蓝色为输入,上面绿色为输出
这一系列的反操作并不是样本图像,也没有生成新的图像,就是一个中间层的投影得到的
可视化
左边的图是第二层卷积核得到的特征图通过反卷积 deconvnet之后映射回原像素空间可视化得到的图像
- 所以在这里可以明白,这篇论文就是要看到每一层中间层所提取到的Feature Map到底是什么样的
- 层数增大,提取的特征越高级。浅层提取长宽size,轮廓,波边缘。深层提取语义信息
- Feature Map:卷积核卷出来的
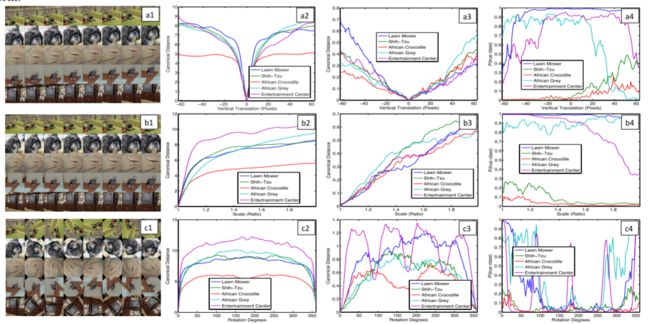
平移-缩放-旋转
- a-b-c对应平移-缩放-旋转
- 1-2-3对应,变换后图像经过1层后与原图像同样处理两者之间的欧氏距离,变换后图像经过7层后与原图像同样处理两者之间的欧氏距离,变换后网络对正确类别对应的概率
- 平移与旋转较为明显
- 浅层稍微变化一点,就会引起突变,深层变化较小
卷积核选择
- 步长由4改为2,大小由11-11改为7-7
- 改变之后没有特别混乱的网格出现
ZF Net与AlexNet

在稍微更改了第一层之后,分类性能提升了,下图为两个网络结构可视化特征图
上图(a)为没有经过裁剪的图片经过第一个卷积层后的特征可视化图,注意到有一个特征全白,(b)为AlexNet中第一个卷积层特征可视化图,(c)为ZFNet中第一个卷积层可视化图,可以看到相比前面有更多的独特的特征以及更少的无意义的特征,如第3列的第3到6行,(d)为AlexNet中第二个卷积层特征可视化图,(e)为ZFNet中的第二个卷积层特征可视化图,可以看到(e)中的特征更加干净,清晰,保留了更多的第一层和第二层中的信息
验证模型可感知具体位置
可以用实验来证明一下,即用一个灰色小方块来挡住图像中的目标,然后再观测输出的分类情况来分析,如下图
上图为对三个不同的测试图片中的不同位置用灰色小方块进行掩盖后,观测分类输出的改变情况。第一列(a)为原始测试图片,第二列(b)为某个区域被灰色小方块掩盖后的网络结构中第五层的特征图,第三列(c)为将第五层的特征图投影到输入图像的可视化图像,第一行表明最强烈的特征表现在狗狗的面部区域,(d)为正确分类概率的图,(e)为最有可能的标签
上述结果表明,如果图像中的目标被遮挡,那么被正确分类的概率会显著降低,这表明这种可视化与激发特征图的图像结构式真正对应上的。即大概能知道位置遮挡目标识别则不利于识别,遮挡非目标识别,则有利于识别
不同部位的相关性

不同的狗遮挡相同的部位,得到的预测结果近似,进而表明模型隐式地定义了不同部位的相关性
ZFNet论文
- 深度可视化工具:ZFNet 的一大贡献是提供了一种观察和理解卷积网络内部活动的方法。这种可视化方法使我们能够观察到每一层的特征如何捕捉到图像的不同方面
- 结构调整:ZFNet 对 AlexNet 的结构进行了微调。它主要对第一层的卷积核大小、步长和数量进行了调整。这表明微调现有网络结构的某些部分可以显著提高性能
- 早期模型:与当今的深度学习模型(如 ResNet、BERT、GPT 等)相比,ZFNet 是一个相对较早期的模型。因此,它在参数数量和模型深度上都相对较少。如果你正在寻找最新的技术或最佳性能,可能需要考虑后来的模型
- 计算效率:尽管ZFNet较AlexNet有所改进,但与后来的一些优化模型(如 MobileNet、EfficientNet 等)相比,它在计算效率上可能不够理想。如果计算资源有限,可能需要考虑其他更轻量级的模型
- 过拟合:与所有深度学习模型一样,ZFNet 也有过拟合的风险。需要确保使用适当的正则化技巧,如 dropout 和数据增强
- 数据预处理:正如大多数深度学习模型所强调的,合适的数据预处理(例如归一化、中心化等)对于ZFNet的性能至关重要
- 硬件兼容性:当ZFNet首次发布时,深度学习框架和GPU加速库可能与现今的版本不同。如果你计划从头开始实现ZFNet,需要确保你的实现与当前的硬件和软件环境兼容
对比AlexNet与ZFNet
- 网络深度:
- 两者都是 8 层深的网络(5 个卷积层和 3 个全连接层)
- 第一层的调整:
- AlexNet:第一层使用了 11x11 大小的卷积核,步长为 4
- ZFNet:第一层使用了 7x7 大小的卷积核,步长为 2。这是基于可视化结果的调整,这种调整能更好地捕获图像的细节信息
- 卷积核数量:
- 在某些层,两者的卷积核数量略有不同。例如,ZFNet 的第三、第四、和第五卷积层的卷积核数量分别为 384、384 和 256,而 AlexNet 的相应层数的卷积核数量为 384、384 和 256
- 激活函数:
- 两者都使用了 ReLU 作为激活函数
- 局部响应归一化(LRN):
- AlexNet 使用了局部响应归一化 (LRN)。ZFNet 也继承了这个特性,但是它的作用和实际效果在现代深度学习模型中已经变得有点存疑
- 池化:
- 两者都使用了最大池化
- 全连接层:
- 两者在全连接层的结构上相似,但权重初始化和其他细节可能略有差异
- Dropout:
- AlexNet 在其全连接层使用了 dropout 来减少过拟合。ZFNet 也采用了相同的策略
- 可视化:
- ZFNet 的一个主要贡献是提供了一种观察和理解卷积网络内部工作的方法,这在 AlexNet 的原始论文中并没有强调
VGGNet(Visual Geometry Group Net)
VGGNet结构
跳转到参考链接
视频-VGGNet论文关键点解读
视频-论文详细
- 神经网络的深度与其性能之间的关系


- 输入层
- 功能:接受图像输入
- 输入:224x224x3
- 输出:224x224x3
- 作用:为网络提供原始的像素值输入。
- 卷积层1 (Conv1)
- 功能:初步提取图像中的低级特征,如边缘和颜色。
- Conv1-1:
- 输入: 224x224x3
- 操作: 64个3x3滤波器,步长为1,padding为’same’
- 输出: 224x224x64
- Conv1-2:
- 输入: 224x224x64
- 操作: 64个3x3滤波器,步长为1,padding为’same’
- 输出: 224x224x64
- Maxpooling:
- 输入: 224x224x64
- 操作: 2x2池化,步长为2
- 输出: 112x112x64
- 作用: 减小特征图的尺寸,增强特征的鲁棒性。
- 卷积层2 (Conv2)
- 功能:继续提取更复杂的低级到中级特征。
- Conv2-1:
- 输入: 112x112x64
- 操作: 128个3x3滤波器,步长为1, padding为’same’
- 输出: 112x112x128
- Conv2-2:
- 输入: 112x112x128
- 操作: 128个3x3滤波器,步长为1, padding为’same’
- 输出: 112x112x128
- Maxpooling:
- 输入: 112x112x128
- 操作: 2x2池化,步长为2
- 输出: 56x56x128
- 作用: 进一步压缩特征图,加强特征表示。
- 卷积层3 (Conv3)
- 功能:提取中级特征,例如纹理和复杂的图案。
- Conv3-1:
- 输入: 56x56x128
- 操作: 256个3x3滤波器,步长为1, padding为’same’
- 输出: 56x56x256
- Conv3-2:
- 输入: 56x56x256
- 操作: 256个3x3滤波器,步长为1, padding为’same’
- 输出: 56x56x256
- Conv3-3:
- 输入: 56x56x256
- 操作: 256个3x3滤波器,步长为1, padding为’same’
- 输出: 56x56x256
- Maxpooling:
- 输入: 56x56x256
- 操作: 2x2池化,步长为2
- 输出: 28x28x256
- 作用: 进一步减小特征图大小,加强网络的表达能力。
- 卷积层4 (Conv4)
- 功能:继续提取中到高级的特征,能够捕捉图像中的复杂对象和结构。
- Conv4-1:
- 输入: 28x28x256
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 28x28x512
- Conv4-2:
- 输入: 28x28x512
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 28x28x512
- Conv4-3:
- 输入: 28x28x512
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 28x28x512
- Maxpooling:
- 输入: 28x28x512
- 操作: 2x2池化,步长为2
- 输出: 14x14x512
- 作用: 通过池化进一步压缩特征表示。
- 卷积层5 (Conv5)
- 功能:提取最高级的特征,为分类提供强有力的信息。
- Conv5-1:
- 输入: 14x14x512
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 14x14x512
- Conv5-2:
- 输入: 14x14x512
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 14x14x512
- Conv5-3:
- 输入: 14x14x512
- 操作: 512个3x3滤波器,步长为1, padding为’same’
- 输出: 14x14x512
- Maxpooling:
- 输入: 14x14x512
- 操作: 2x2池化,步长为2
- 输出: 7x7x512
- 作用: 在这一阶段进一步提取特征。
- 全连接层 (FC layers)
- 功能:进行分类的决策。
- FC1:
- 输入:
几个重要的问题
- 输入:网络处理的是固定大小为 224x224 的 RGB 图片。预处理步骤仅为从每个像素中减去 ImageNet 训练集的 RGB 平均值
- 卷积层:
- 主要使用 3x3 的卷积核,它是最小尺寸的卷积核,能够捕获图像的上下、左右和中心信息
- 在某些配置中,还使用了 1x1 的卷积滤波器来进行输入通道的线性变换
- 滑动步长为 1
- 使用 “Same” 填充方式,即对 3x3 的卷积层,padding 为 1
- 池化层:
- 使用 5 个最大池化层,这些池化层接在某些卷积层后面(而非所有)
- 池化窗口为 2x2,滑动步长为 2
- 全连接层:
- 网络后部分有 3 个全连接层
- 前两层各有 4096 个通道
- 第三层是分类层,含有 1000 个通道,对应 ImageNet 的 1000 个类别
- 激活函数:
- 所有隐藏层均使用 ReLU 作为非线性激活函数
- 输出:
- 使用 softmax 函数处理,得出图像属于每个类别的概率
这个网络结构充分利用了多个卷积层、池化层和全连接层的组合,配合 ReLU 激活函数,能够在大型数据集(如 ImageNet)上达到很好的效果
3x3卷积核的作用(优势)
两个3×3的卷积层串联相当于1个5×5的卷积层(二者具有等效感受野5x5),3个串联的3×3卷积层串联的效果相当于一个7×7的卷积层
两层3-3的卷积核卷积操作之后的感受野是5-5,其中卷积核(filter)的步长(stride)为1、padding为0,如图所示:
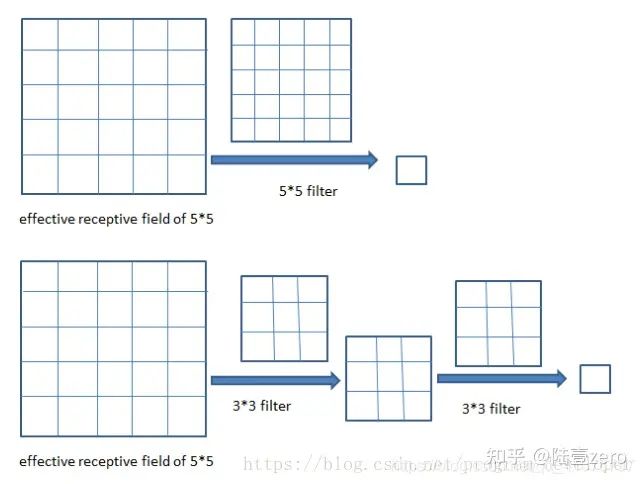
三层3-3卷积核操作之后的感受野是7-7,其中卷积核的步长为1,padding为0,如图所示:
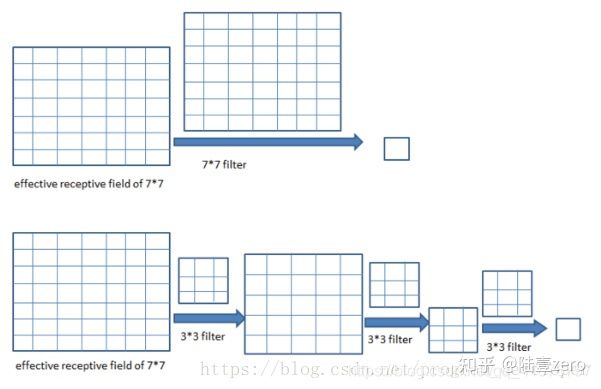
- 两个3 x 3就能有5 x 5的感受野,三个3 x 3就能有7 x 7的感受野(画图就能理解),而这些3 x 3的卷积层之间还有两个或三个ReLU层,ReLU的非线性性质能使网络的辨别(拟合)能力更强(相较于大卷积核仅一层ReLU)
- 大卷积核参数多,计算量大
1 x 1卷积核作用

增加网络深度(增加非线性映射次数)
首先直接从网络深度来理解,1x1的卷积核虽小,但也是卷积核,加1层卷积,网络深度自然会增加1x1卷积核,可以在保持feature map尺度不变的(即不损失分辨率)的前提下大幅增加非线性特性(利用后接的非线性激活函数),把网络做的很深。并且1x1卷积核的卷积过程相当于全连接的计算过程,通过加入非线性激活函数,可以增加网络的非线性,使得网络可以表达更复杂的特征
其实,这涉及到感受野的问题,我们知道卷积核越大,它生成的 featuremap 上单个节点的感受野就越大,随着网络深度的增加,越靠后的 featuremap 上的节点感受野也越大。因此特征也越来越抽象
但有的时候,我们想在不增加感受野的情况下,让网络加深,为的就是引入更多的非线性
而 1x1 卷积核,恰巧可以办到
我们知道,卷积后生成图片的尺寸受卷积核的大小和跨度影响,但如果卷积核是 1x1 ,跨度也是1,那么生成后的图像大小就并没有变化
但通常一个卷积过程包括一个激活函数,比如 Sigmoid 和 Relu
所以,在输入不发生尺寸的变化下,却引入了更多的非线性,这将增强神经网络的表达能力
升维/降维
其实这里的升维、降维具体指的是通道数的变化,当我们确定了卷积核尺寸后,我们height、width都不变,那么这里的维度具体指的就是channels。我们通过改变卷积核的数量来改变卷积后特征图的通道channels来实现升维、降维的效果。这样可以将原本的数据量进行增加或者减少
下面举两个例子就能明显看到效果:


使用1x1卷积核升维/降维的原因:
当我们仅仅只是想要改变通道数的情况下,1x1卷积核是最小的选择,因为大于1x1的卷积核无疑会增加计算的参数量,内存也会随之增大,所以只想单纯的去提升或者降低特征图的通道,选用1x1卷积核最为合适, 1x1卷积核会使用更少的权重参数数量
- 跨通道的信息交互
- 1x1卷积核只有一个参数,当它作用在多通道的feature map上时,相当于不同通道上的一个线性组合,实际上就是加起来再乘以一个系数,但是这样输出的feature map就是多个通道的整合信息了,能够使网络提取的特征更加丰富
- 使用1x1卷积核,实现降维和升维的操作其实就是 channel 间信息的线性组合变化
- 比如:在尺寸 3x3,64通道个数的卷积核后面添加一个尺寸1x1,28通道个数的卷积核,就变成了尺寸3x3,28尺寸的卷积核。 原来的64个通道就可以理解为跨通道线性组合变成了28通道,这就是通道间的信息交互
- **注意:**只是在通道维度上做线性组合,W和H上是共享权值的滑动窗口
- 减少卷积核参数(简化模型)


VGGNet论文
- 卷积核大小:
- VGGNet 的一个核心观点是,两个 3×33×3 的卷积层(堆叠在一起)比一个 5×55×5 的卷积层有更少的参数并且更加表现力。同样,三个 3×33×3 的卷积层等效于一个 7×77×7 的卷积层。要注意这一点,并理解这种设计的动机
- 网络的深度:
- 论文中描述了从 11 层到 19 层不等的不同版本的 VGGNet(如 VGG-11、VGG-16、VGG-19)。需要注意的是,更深的网络并不总是导致更好的性能
- 参数数量:
- 尽管 VGGNet 结构简单直观,但它包含大量的参数,尤其是在全连接层中。这使得 VGGNet 需要大量的内存和计算资源
- 没有其他特殊的技巧:
- 与其他一些著名的深度学习模型相比,VGGNet 的一个突出特点是其简单和均匀的架构。除了使用小卷积核和多层网络外,它没有其他特殊的技巧或组件
- 预处理:
- 在 VGG 的论文中,他们使用了特定的输入预处理。如果你打算复现论文中的结果或使用预训练的权重,确保正确地应用预处理
ZFNet与VGGnet
ZFNet
- 发展背景:
- ZFNet 是 2013 年 ImageNet ILSVRC 的获胜模型
- 它实际上是对AlexNet的一种调整,优化了一些超参数
- 结构特点:
- ZFNet 有 8 个层,其中 5 个是卷积层,3 个是全连接层
- 使用了更小的卷积核 (7x7、5x5、3x3) 和步长
- 使用了叠加的卷积层,但没有像 VGGNet 那样大量地使用这种结构
- 目标:
- ZFNet 的主要目的是通过更好地可视化每一层的特征来理解和解释深度卷积网络的内部工作原理
- Zeiler 和 Fergus 使用了一种叫做 DeconvNet 的方法,通过它可以对每一层产生的特征图进行反卷积操作,以更好地理解每一层所捕获的特征
VGGNet:
- 发展背景
- VGGNet 是 2014 年 ImageNet ILSVRC 的第二名模型,由牛津大学的 Visual Geometry Group 开发
- 结构特点
- VGGNet 的主要特点是使用多个连续的 3x3 卷积核来代替大尺寸的卷积核(如 5x5、7x7)
- VGG 提出了多个版本,其中 VGG-16 和 VGG-19 最为流行,代表着网络中的权重层数
- 具有 13 个或 16 个卷积层,再加上3个全连接层,使得 VGGNet 相当深
- 目标
- VGG 的主要目标是通过使用简化的网络结构来展示,重复使用小的卷积核可以达到与复杂网络同样甚至更好的效果
对比:
- 深度:VGGNet 显然更深。ZFNet 有 8 个层,而 VGG-16 有 16 个权重层
- 卷积核尺寸:ZFNet 使用了不同尺寸的卷积核(7x7、5x5、3x3),而 VGGNet 主要使用了 3x3 的卷积核
- 复杂性:尽管 VGGNet 更深,但其结构更为统一和简化
- 可解释性:ZFNet 的一个主要贡献是关于卷积网络如何工作的深入可视化,而 VGGNet 主要关注于提供一个简单且深入的模型来提高性能
HOOK
在深度学习中,钩子(hook)是一种机制,用于在模型的前向传播或反向传播过程中获取中间结果或梯度,并进行相应的操作或分析。它们提供了一种灵活的方式来访问和修改模型的内部状态,以满足特定的需求
什么是钩子?
在 PyTorch 中,钩子可以被视为一个函数,该函数可以被附加到任何
nn.Module(例如卷积层、全连接层等)上。一旦钩子被添加,每次执行这个模块时,这个函数就会被调用。PyTorch 提供了三种类型的钩子:
register_forward_pre_hook: 在前向传播开始前执行register_forward_hook: 在前向传播后执行register_backward_hook: 在反向传播后执行示例代码
假设我们有一个简单的神经网络,我们希望在前向传播后打印输出的统计信息:
import torch import torch.nn as nn # 定义简单的网络 class SimpleNet(nn.Module): def __init__(self): super(SimpleNet, self).__init__() self.fc = nn.Linear(5, 3) def forward(self, x): return self.fc(x) # 钩子函数 def print_statistics(module, input, output): print("Inside " + module.__class__.__name__) print("-" * 40) print("Output Stats") print("Mean: ", output.data.mean()) print("Std: ", output.data.std()) print("=" * 40) # 实例化模型 model = SimpleNet() # 添加钩子 hook = model.fc.register_forward_hook(print_statistics) # 使用模型进行前向传播 x = torch.randn(10, 5) y = model(x) # 为了清理,不再需要钩子时 hook.remove()使用步骤:
- 定义模型:首先,我们定义了一个简单的神经网络
SimpleNet- 定义钩子函数:钩子函数通常接受三个参数:模块、输入和输出。在上面的例子中,我们的钩子函数
print_statistics打印了输出的平均值和标准差- 注册钩子:使用
register_forward_hook方法将钩子函数附加到我们想要的模块(在本例中为model.fc)- 前向传播:当我们执行模型的前向传播时,钩子函数会自动被调用,并打印输出的统计信息
- 移除钩子:一旦我们不再需要钩子,为了避免额外的计算,我们应该使用
hook.remove()方法来删除它def hook(model, layer_input, layer_output): """ 添加到当前层次的forward之后执行的hook(钩子) :param model: 当前模型 :param layer_input: 当前模型forward方法的所有参数的输入,是一个tuple/list的形式 :param layer_output: 当前模型forward方法的返回结果 :return: 如果返回None,不会对返回值产生影响,如果返回非None的值,那么当前hook的返回值 会替代forward的返回值 """ print("xxx") pass remove取消hook以下是钩子的一些常见用途:
- 特征提取:
- 目的:获取模型中的中间特征
- 应用:用于特征的可视化、选择等
- 操作:注册钩子于特定层,抓取该层的输出特征图
- 梯度分析:
- 目的:观察和分析模型的梯度
- 应用:梯度的可视化、统计分析和实时修改
- 操作:注册钩子于特定层,获取该层的梯度信息
- 模型解释:
- 目的:解析模型的预测决策
- 应用:生成如类激活映射(CAM)等可视化工具,显示模型在做预测时的关注重点
- 操作:注册钩子于模型的输出层,分析其预测
- 模型修改与优化:
- 目的:改变模型的行为或参数
- 应用:根据需求自定义模型的输出和梯度
- 操作:注册钩子于多个层,实时获取和调整输出或梯度
GoogLeNet
问题综述
跳转到参考链接
视频-GoogLeNet网络详解
传统的提高神经网络性能的方法:
- 增加深度(
网络层次数量)- 增加宽度(
每一层的神经元数量)该方案简单、容易但有两个主要的缺点:
- 容易过拟合
- 需要更强的计算能力
过去的解决方法及问题:
稀疏连接:
解决以上两个问题的一个基本的方式就是引入稀疏性,将全连接层替换为稀疏的全连接层,甚至是卷积层
稀疏连接有两种方法:
- 空间(spatial)上的稀疏连接,也就是 CNN 。其只对输入图像的局部进行卷积,而不是对整个图像进行卷积,同时参数共享降低了总参数的数目并减少了计算量
- 在特征(feature)维度上的稀疏连接进行处理,也就是在通道的维度上进行处理
针对以上情况,我们希望找到一种方法既能保持网络结构的稀疏性,又能利用密集矩阵的高计算性能。大量的文献表明可以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能,据此论文提出了名为Inception的结构来实现此目的

稀疏矩阵分解为密集矩阵运算的例子,可以发现,运算量确实降低不少
Inception module
原始版本:四个分支,每个分支卷积后的feature map分辨率大小是相同的,于是就可以将其堆叠起来,作为下一层的输入(注意这里选择1 x 1、3 x 3、5 x 5仅是为了方便而非必须,而VGGNet论文是解释了大卷积核的缺点的)
举个例子:假设上一层输出是28 x 28 x 192,第一个分支卷积核是1 x 1 x 64,padding = 0,stride = 1,输出是28 x 28 x 64;第二个分支卷积核是3 x 3 x 128,padding = 1,stride = 1,输出就是28 x 28 x 128,第三个分支卷积核是5 x 5 x 32,padding = 2,stride = 1,输出就是28 x 28 x 32;第四个分支和第二个差不多,padding = 1,stride = 1,输出是28 x 28 x 192(和输入一样,这也是问题所在),于是这四个分支的输出可以拼接在一起
原始版本有两个问题:
- pooling分支的输出和输入维度完全相同,拼接之后会导致输出变得越来越大
- 由前一个问题导致后面的3 x 3和5 x 5计算量很大
降维版本:在3 x 3的前面、5 x 5的前面、pooling层的后面加1 x 1卷积降维,这样做第一可以使维度变得可控,减少后面的计算量(即使被降维成低维度了也可以包含大量的信息),第二和VGGNet的解释一样,加入的1 x 1后的ReLU可以增加网络的非线性表达能力
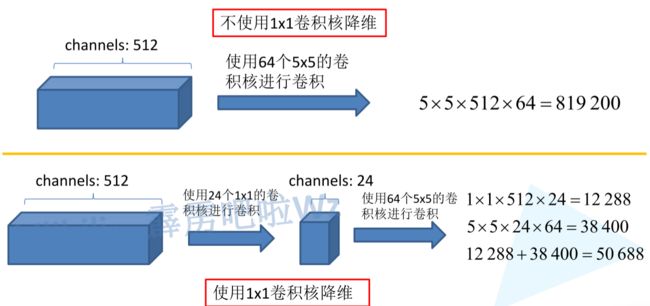
采用Inception结构的好处:
- 可以自己控制每一层的卷积核个数,从而使得计算复杂度可控
- 此结构的每个分支从多个尺度抽象出特征,这又与多尺度提取视觉信息相符
- 比结构相似但没有采用Inception结构的网络快2到3倍
模型

输入是224 x 224 x 3,并减均值;前几层还是正常的卷积层,后面才用Inception;所有卷积层后面都有ReLU;最后的平均池化层和全连接层可以使fine-tuning更加方便;有两个辅助分类器,在反向传播过程中会将辅助分类器的loss乘以0.3的权重再加到总loss中,注意辅助分类器在预测阶段不会使用
最终模型:
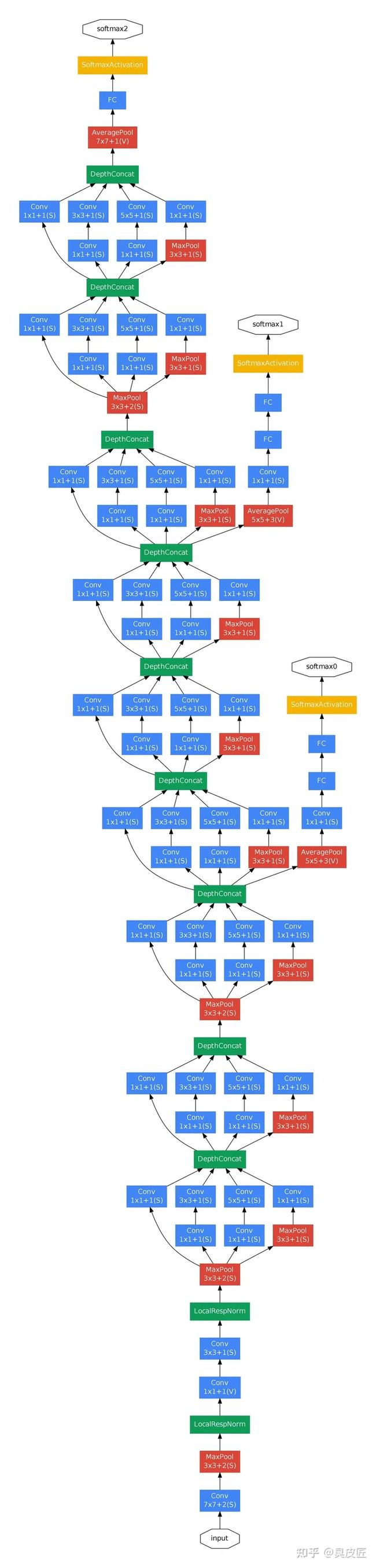
GoogLeNet(Inception v1)的详细结构与尺寸如下:>
- 输入层
- 功能:接受图像输入
- 输入尺寸:224x224x3
- 作用:为网络提供原始的像素值输入
- 卷积层1 (Conv1)
- 功能:初步提取图像中的低级特征
- 卷积操作: 使用64个7x7的滤波器,步长为2
- 作用:通过大的滤波器尺寸捕获更多的空间信息
- 输出尺寸: 112x112x64
- 最大池化: 3x3的窗口,步长为2
- 作用:降低特征维度,增强模型的鲁棒性。
- 输出尺寸: 56x56x64
- 局部响应归一化 (LRN)
- 作用:增强模型的泛化能力,减少过拟合。
- 卷积层2 (Conv2)
- 功能:继续提取更复杂的低级到中级特征。
- 卷积操作: 先使用1x1的滤波器,然后使用3x3的滤波器
- 作用:通过逐渐增加的滤波器尺寸来捕获不同的空间信息
- 输出尺寸: 56x56x192
- 最大池化: 3x3的窗口,步长为2
- 作用:进一步降低特征维度,提取显著特征
- 输出尺寸: 28x28x192
- 局部响应归一化 (LRN)
- 作用:增强特征的鲁棒性,提供更好的泛化
- Inception模块组 (3a, 3b)
- 功能:通过不同尺寸的滤波器并行地提取特征
- 3a 输出尺寸: 28x28x256
- 3b 输出尺寸: 28x28x480
- 最大池化: 3x3的窗口,步长为2
- 作用:进一步压缩特征并保留显著信息
- 输出尺寸: 14x14x480
- Inception模块组 (4a - 4e)
- 功能:利用不同尺寸的滤波器并行提取更高级的特征
- 4a 输出尺寸: 14x14x512
- 4b 输出尺寸: 14x14x512
- 4c 输出尺寸: 14x14x512
- 4d 输出尺寸: 14x14x528
- 4e 输出尺寸: 14x14x832
- 最大池化: 3x3的窗口,步长为2
- 作用:进一步减小特征维度,同时保留显著特征
- 输出尺寸: 7x7x832
- Inception模块组 (5a, 5b)
- 功能:在更高级别上并行提取特征
- 5a 输出尺寸: 7x7x832
- 5b 输出尺寸: 7x7x1024
平均池化层
- 功能:对特征进行空间平均,减少计算量
- 平均池化窗口: 7x7, 步长为1
- 作用:将特征维度减少至1x1的尺寸,这样为全连接层做准备
- 输出尺寸: 1x1x1024
全连接层 (FC layers)
- 功能:对提取的特征进行分类
- 输出尺寸: 1x1x1000
- 作用:将特征转化为对应于1000个类别的概率分布
Softmax层
- 功能:转换模型输出为概率分布
- 输出尺寸: 1x1x1000
- 作用:确保模型输出代表每个类别的概率,并且所有类别的概率总和为1
优点
- 引入了Inception结构(融合不同尺度的特征信息)
- 使用1x1的卷积核进行降维以及映射处理
- 添加两个辅助分类器帮助训练
- 丢弃全连接层,使用平均池化层(大大减少模型参数)
训练细节
- 多尺度采样(注意这里是训练时,和预测时不一样):从原始图片裁剪出用于训练的图片,裁剪出的尺寸大小 从8%到100%的均匀分布随机选择一个,纵横比从3/4和4/3随机选择一个
- 数据集:GoogleNet最初是在ImageNet数据集上进行训练的,该数据集包含超过1.2万个类别和100万个图像。在训练过程中,使用了数据增强技术来扩充训练集,包括随机裁剪、水平翻转、色彩抖动等
- 损失函数:GoogleNet使用交叉熵损失函数来优化模型,这是一种常见的用于分类任务的损失函数
- 优化器:GoogleNet使用了基于动量的随机梯度下降(SGD)优化器来更新模型参数。在训练过程中,还使用了学习率衰减策略来逐渐降低学习率,以便更好地收敛
- 正则化:为了防止过拟合,GoogleNet使用了L2正则化,通过对模型参数进行惩罚,来减少参数的过度拟合
- Dropout:GoogleNet还使用了Dropout技术来随机丢弃一部分神经元,以减少模型的过拟合
- **批量归一化:**GoogleNet引入了批量归一化(Batch Normalization)技术,来加速收敛并提高模型的鲁棒性
- 模型结构:GoogleNet的模型结构采用了Inception模块,这是一种多分支结构,可以同时提取不同尺度的特征。同时,GoogleNet还使用了全局平均池化层来减少模型的参数量,从而提高模型的泛化能力
GoogLeNet V2
以下是对 Inception v2 的主要特点和改进的总结:
- Batch Normalization (BN):
- 在每个卷积层之后都添加了 Batch Normalization。BN 可以加速网络的收敛,允许使用更大的学习率,并具有某种正则化效果
- 由于 BN 的正则化效果,可以减少或完全不使用 dropout
- 去除5x5的卷积:
- 为了减少计算成本,5x5的卷积被两个连续的3x3的卷积所替代。这种方法的灵感来自 VGG 网络,其中使用连续的小卷积核可以得到与大卷积核相同的感受野,但计算成本更低
- 更多的分解:
- 除了将5x5的卷积替换为两个3x3的卷积外,Inception v2 还将 3x3 的卷积替换为 1x3 和 3x1 的卷积。这种 “卷积分解” 能够进一步减少计算成本
- 优化的池化策略:
- 在某些 Inception 模块中,2x2的最大池化与3x3的卷积被并行连接。这允许信息通过两种路径流动:一种是经过池化的下采样路径,另一种是空间分辨率不变的卷积路径
- 更高效的网络设计:
- 通过上述改进,Inception v2 在保持模型尺寸和计算成本相当时实现了更高的准确性
流程:
输入层:
- 输入尺寸: 224×224×3
卷积层1 (Conv1):
- 卷积操作: 64个7x7的滤波器, 步长为2
- 输出尺寸: 112x112x64
- 最大池化: 3x3窗口,步长为2
- 输出尺寸: 56x56x64
- 批量归一化 (BN)
卷积层2 (Conv2):
- 使用两阶段卷积:首先是1x1滤波器,然后是3x3滤波器
- 输出尺寸: 56x56x192
- 最大池化: 3x3窗口,步长为2
- 输出尺寸: 28x28x192
- 批量归一化 (BN)
Inception模块组 (3a, 3b,…):
- 结合1x1, 3x3, 5x5的卷积和3x3的最大池化。
- 例如, 3a 输出尺寸: 28x28x256
- 批量归一化 (BN) 在每个子模块之后。
辅助分类器1:
- 平均池化: 5x5, 步长为3
- 输出尺寸: 4x4x512 (此尺寸是假设的,与实际模型可能有所不同)
- 卷积: 128个1x1滤波器
- 输出尺寸: 4x4x128
- 全连接层: 1024神经元
- Dropout: 70%
- 全连接层: 1000神经元 & Softmax激活
Inception模块组 (4a - 4e):
- 结合多尺度特征,如前面的模块组
- 例如, 4e 输出尺寸: 14x14x832
- 最大池化: 3x3窗口,步长为2
- 输出尺寸: 7x7x832
辅助分类器2:
- 结构与辅助分类器1相似
Inception模块组 (5a, 5b):
- 继续融合不同尺度的特征
- 例如, 5b 输出尺寸: 7x7x1024
平均池化层:
- 7x7的平均池化窗口, 步长为1
- 输出尺寸: 1x1x1024
Dropout层:
- Dropout率为40%
- 全连接层 (FC layers):
- 1000个神经元用于分类
- 输出尺寸: 1x1x1000
- Softmax层:
- 输出尺寸: 1x1x1000
GoogleNet V3
以下是对 Inception v3 的主要特点和改进的总结:
- 更深的网络结构:
- Inception v3 比前面的版本更深,这意味着模型具有更多的层
- 进一步的分解:
- 7x7 的卷积被分解为一系列 1x7 和 7x1 的卷积。这种方法进一步延续了 Inception v2 中引入的卷积分解策略,可以减少参数数量和计算量
- 更多的 Inception 模块:
- Inception v3 引入了更多的模块设计,包括不同大小的卷积核和并行结构,以捕获多尺度的特征
- 标签平滑:
- 为了缓解过拟合和改善训练稳定性,Inception v3 使用了标签平滑技术。这种技术主要涉及对训练标签进行柔和的调整,以使其不完全是硬标签
- 更少的池化操作:
- 通过减少池化操作,Inception v3 保持了更高的空间分辨率,这有助于捕获更精细的图像特征
- 更有效的辅助分类器:
- 与 Inception v1/v2 中的辅助分类器不同,Inception v3 的辅助分类器与主要分类器更加接近
- 更大的图像输入:
- Inception v3 使用了 299x299 的输入图像,而不是之前版本中的 224x224。这提供了更多的上下文信息,并可以捕获更多的图像细节
流程:
输入层:
- 输入尺寸: 299×299×3
卷积层1:
- 卷积操作: 使用32个3×3的滤波器,步长为2
- 输出尺寸: 149x149x32
卷积层2:
- 卷积操作: 使用32个3×3的滤波器
- 输出尺寸: 147x147x32
卷积层3:
- 卷积操作: 使用64个3×3的滤波器
- 输出尺寸: 147x147x64
- 最大池化: 3x3窗口,步长为2
- 输出尺寸: 73x73x64
卷积层4:
- 卷积操作: 使用80个1×1的滤波器
- 输出尺寸: 73x73x80
卷积层5:
- 卷积操作: 使用192个3×3的滤波器
- 输出尺寸: 71x71x192
- 最大池化: 3x3窗口,步长为2
- 输出尺寸: 35x35x192
Inception模块组:
- 包括多个Inception模块,每个模块有不同大小的卷积、最大池化和平均池化层。这些模块通过不同尺寸的卷积来捕捉不同尺度的特征。
辅助分类器:
- 平均池化: 5x5, 步长为3
- 输出尺寸: 取决于前面的层
- 卷积: 某数量的1x1滤波器
- 全连接层
- Dropout
- 全连接层 & Softmax激活
Inception模块组(继续):
- 与之前类似,但有更多的输出特征图
平均池化层:
- 8x8的平均池化窗口
- 输出尺寸: 1x1x某数量的特征图
- Dropout层:
- Dropout率为40%
- 全连接层:
- 某数量的神经元用于分类
- 输出尺寸: 1x1x类别数
- Softmax层:
- 输出尺寸: 1x1x类别数
GoogleNet V4
以下是对 Inception v4 的主要特点和改进的总结:
- 结构改进:
- Inception v4 介绍了更多的优化的 Inception 模块,这些模块设计得更为复杂和高效
- 引入残差连接:
- Inception v4 的一部分是 Inception-ResNet,这里采用了与 ResNet 类似的快速通道或残差连接。这些连接允许梯度更容易地在深层网络中流动,有助于训练更深的模型而不遇到梯度消失问题
- 减少过滤器的数量:
- 为了提高计算效率,Inception v4 在某些模块中使用了较少的过滤器
- 更多的扩展:
- Inception v4 的网络结构比 Inception v3 更深,有更多的层,这有助于模型捕获更复杂的特征
- 更大的输入图像尺寸:
- 与 Inception v3 一样,Inception v4 也使用了 299x299 的输入图像大小
- 调整的辅助分类器位置:
- 辅助分类器的位置进行了微调,以便更好地协助训练过程
GoogLenet论文
- Inception模块:GoogLeNet中的基本构建模块是Inception模块,它在同一层内包含多种不同尺寸的卷积核和池化操作,最后将这些操作的结果沿深度维度进行堆叠
- 网络的深度:GoogLeNet比以前的深度学习模型更深,但不是仅仅堆叠更多的层。它的设计是为了优化性能和计算效率
- 辅助分类器:为了解决深度网络中的梯度消失问题,GoogLeNet在网络的中部引入了两个辅助分类器。这些分类器在训练时加入,但在测试时被忽略
- 参数数量:尽管GoogLeNet是一个非常深的网络,但由于其有效的设计,它的参数数量实际上比其他一些较小的网络(如AlexNet)要少。这使得GoogLeNet更易于训练,而且对于部署到资源受限的环境(如移动设备)也更加友好
- 计算效率:Inception模块是设计得尽可能地减少计算量,而不损失模型性能。这通过1x1的卷积操作来降低特征映射的维度达到的
- 模型集成:在论文的最后,作者使用多个GoogLeNet模型的集成来进一步提高性能
- 模型解释性:尽管GoogLeNet是一个深层和复杂的模型,但作者提供了关于如何可视化和理解模型决策的一些建议
流程:
输入层:
- 输入尺寸: 299×299×3
Stem:
- 初始的一系列卷积、池化和归一化操作。结束后,尺寸约为35x35x384
Inception-A 模块组:
- 这是特定于 Inception v4 的模块,其中包含多个并行的卷积操作,结合在一起
- 经过一系列的 Inception-A 模块后,输出的尺寸仍然为35x35,但深度可能会改变
Reduction-A 模块:
- 尺寸缩减模块,使用卷积和池化来降低尺寸。输出尺寸为17x17
Inception-B 模块组:
- 又一个特定的模块组合,结构与Inception-A不同
- 在这一系列后,输出尺寸仍为17x17
Reduction-B 模块:
- 另一个尺寸缩减模块,输出尺寸为8x8
Inception-C 模块组:
- 这是第三种独特的Inception模块组合,结构与之前的模块不同
- 这一系列后,输出尺寸仍为8x8
平均池化层:
- 8x8的平均池化,没有填充
- 输出尺寸为1x1
Dropout层:
- Dropout率为20%,这有助于减少过拟合
全连接层 (FC layers):
- 用于分类的神经元,输出尺寸取决于分类的类别数。
- Softmax层:
- 用于分类的激活层,输出尺寸与类别数相同
VGGNet与GoogLeNet
- 深度:
- VGGNet: VGGNet(特别是VGG-16和VGG-19)的最大特点是其连续的小型卷积核(3x3)和深层的网络结构。VGG-16有16层,而VGG-19有19层
- GoogLeNet: GoogLeNet更加复杂,使用了所谓的Inception模块,实际上它的深度较浅,但是通过串联多个模块而形成的
- 参数量:
- VGGNet: 由于其深层的结构,VGGNet具有大量的参数,特别是在全连接层。这使得模型占用更多的存储空间,并增加了训练的计算成本
- GoogLeNet: 尽管GoogLeNet是一个深度模型,但它使用Inception模块和多尺度特征,大大减少了所需的参数数量。此外,它没有使用大量的全连接层,这也大大降低了参数数量
- 模块化:
- VGGNet: VGG的设计相对简单和直接,主要是连续的3x3卷积层和2x2的池化层
- GoogLeNet: GoogLeNet引入了Inception模块,这是一个“网络中的网络”结构,它在单一的模块内并行地运行多种大小的卷积和池化操作,并将结果级联在一起
- 全连接层:
- VGGNet: VGGNet在顶部有三个全连接层
- GoogLeNet: GoogLeNet使用了全局平均池化层代替全连接层,大大减少了模型的参数数量
- 输出大小:
- VGGNet: VGG的输出是一个1000维的向量,对应于ImageNet的1000个类
- GoogLeNet: GoogLeNet也是1000维的输出,但由于其结构的复杂性,输出是由多个Inception模块和其他组件生成的
- 辅助分类器:
- VGGNet: VGG没有使用辅助分类器
- GoogLeNet: 为了应对深度网络中的梯度消失问题,GoogLeNet在其中间层中加入了两个辅助分类器,这有助于梯度的反向传播
ResNet
问题综述
Residual Network
跳转到参考链接
视频-ResNet论文关键点解读
视频-论文详细
深度学习的发展从LeNet到AlexNet,再到VGGNet和GoogLeNet,网络的深度在不断加深,经验表明,网络深度有着至关重要的影响,层数深的网络可以提取出图片的低层、中层和高层特征。但当网络足够深时,仅仅在后面继续堆叠更多层会带来很多问题:
- 第一个问题就是梯度爆炸 / 消失(vanishing / exploding gradients),梯度大于1/小于1,这可以通过BN和更好的网络初始化解决
- 第二个问题就是**退化(degradation)**问题,即当网络层数多得饱和了,加更多层进去会导致优化困难、且训练误差和预测误差更大了,注意这里误差更大并不是由过拟合导致的(后面实验细节部分会解释)。作者通过加入残差结构解决退化问题
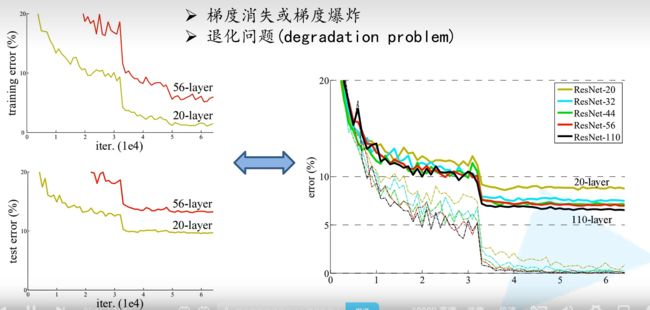
残差结构介绍
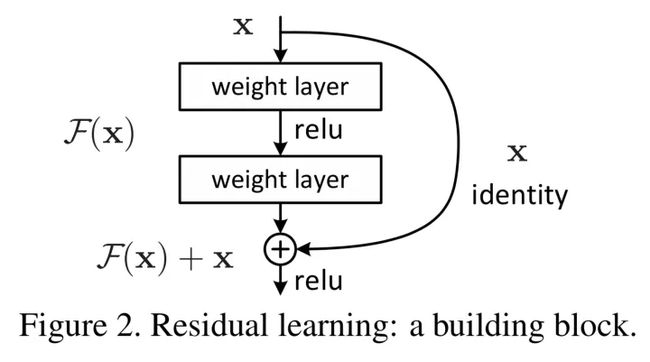
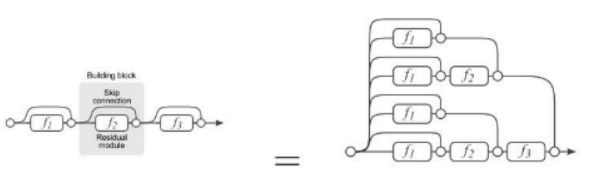
多通路结构,在某些通道被失活时, 仍然可以联通
残差结构为什么有效?
- 恒等映射的容易学习性:在一个深度的神经网络中,增加更多的层理论上不应该导致模型的性能下降,因为网络至少可以学习恒等映射,也就是说,输出等于输入。然而,在实际中,由于梯度消失和爆炸的问题,增加层数确实会导致性能下降。残差结构引入了一个“shortcut”或“skip connection”,这允许层直接学习与输入相关的残差。如果一个残差块需要表示的恒等映射,它可以直接让残差接近0。这种方式让网络更容易学习恒等映射,并且避免了由于层数增加而导致的性能下降
- 缓解梯度消失和梯度爆炸:深度神经网络常常受到梯度消失和梯度爆炸的困扰,这会导致网络难以训练。但由于残差结构中的直接连接,梯度可以直接反向传播到早期的层,这有助于梯度更平稳地流过网络,使得深层网络的训练更加稳定
- 参数的重用:由于残差块直接使用了之前层的输出,这实际上增加了参数的重用。相比于传统的层,残差块可以以较少的参数实现相同或更好的性能
- 提供多尺度特征:由于信息可以直接从一个深层传到一个浅层,这意味着模型能够同时访问不同深度的特征。这为某些任务提供了多尺度的特征,可能有助于捕获在不同尺度上的信息
- 容量控制:虽然深度学习的一个普遍思想是使用更大的模型然后利用正则化来防止过拟合,但残差结构提供了一种更为自然的容量控制方法。如果网络不需要某些残差块,它可以轻易地将这些块的权重设置为零或接近零,从而有效地“关闭”这些块
bottleneck的残差结构
在深度ResNet模型中(如ResNet-50、ResNet-101和ResNet-152),为了减少模型参数和计算量,使用了"bottleneck"结构的残差块
标准的残差块 vs "bottleneck"结构:
标准的残差块:
- 通常包含两个相同大小的卷积层
- 输入首先经过一个卷积层,接着是Batch Normalization和ReLU激活,然后再次经过卷积操作
"bottleneck"结构:
- 包含三个卷积层:一个1x1卷积、一个3x3卷积和另一个1x1卷积
- 输入首先经过1x1卷积,然后是Batch Normalization和ReLU激活,接着是3x3卷积、Batch Normalization和ReLU,最后再经过一个1x1卷积
bottlenec结构的优势:
- 减少参数和计算量:1x1的卷积可以用来减少和增加维度,也称为通道数。因此,通过首先使用1x1卷积来减少维度,然后在维度较低的状态下进行3x3的卷积,之后再使用1x1卷积来恢复原始维度,可以有效地减少整个残差块的参数数量和计算量
- 增加非线性:尽管减少了参数,但由于增加了额外的非线性激活函数,模型的表达能力实际上得到了提高
一个小细节:Res50、Res101、Res152的第一个stage的输入channel维度都是64,跨层连接之后维度并不匹配,所以这里不是恒等映射,还会加一个升维的操作。(从代码中可以看出_make_layer函数中的downsample变量)
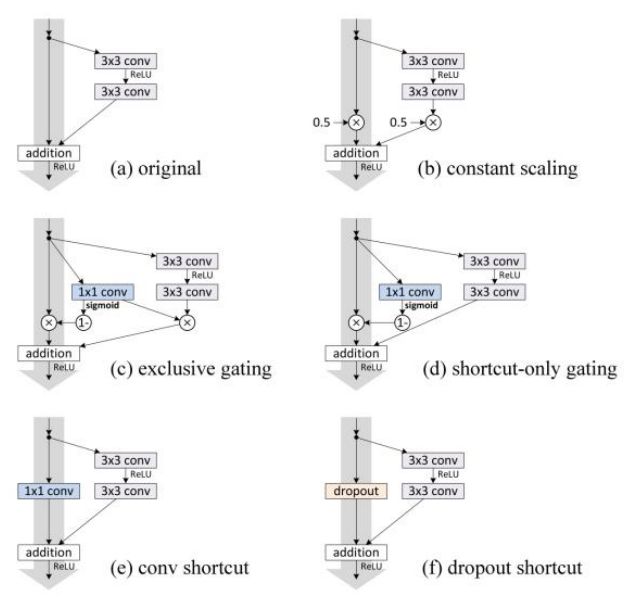
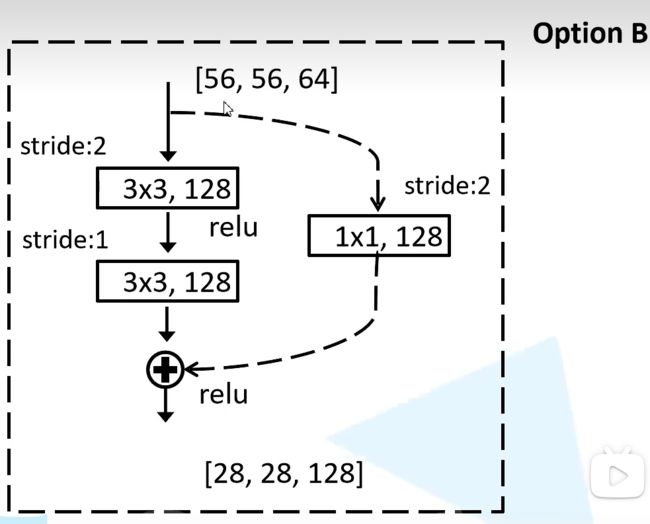
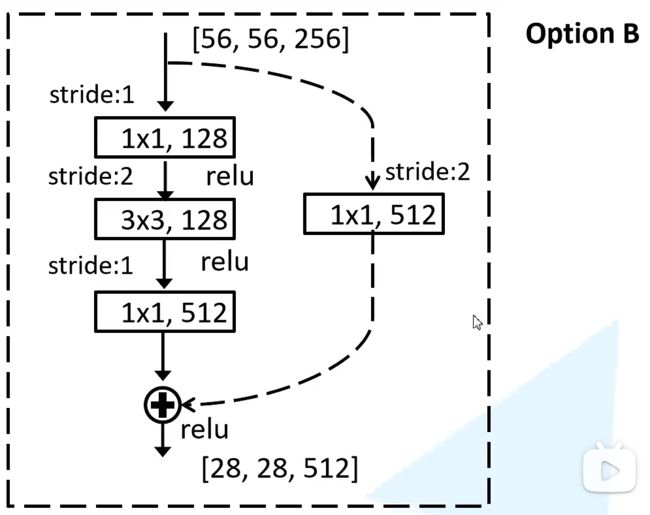
升维有两种方式:
- 第一种是直接全补0,这样做优势是不会增加网络的参数
- 第二种是1 x 1卷积升维
对残差连接进行了三种情况的讨论
- (A)在升维时使用补零
- (B)在升维时使用1x1卷积进行映射
- ©所有残差连接使用1x1卷积进行映射
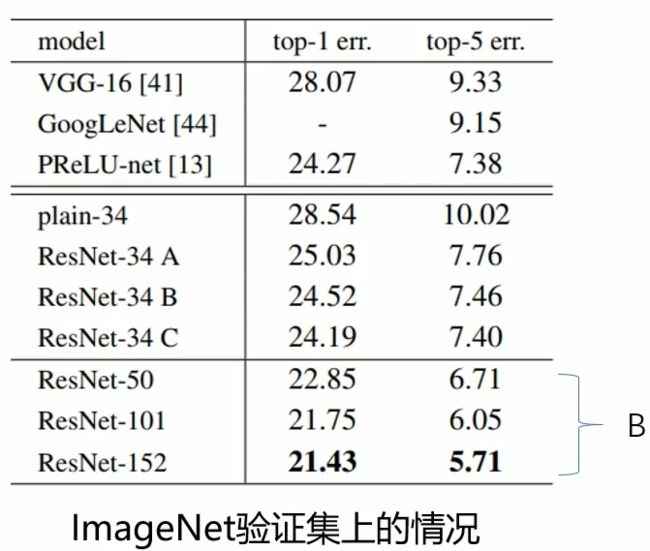
ResNet结构

- downsample通过3-4-5进行
- 50-101-152注意深度与图片尺寸的变化
从上面对残差结构的描述可以看出,残差结构既不增加计算复杂度(除了几乎可以忽略的元素相加),又不增加模型的参数量,同时这也为模型间的比较提供了方便。下图的左边是VGG-19;下图的中间是作者仿照VGG19堆叠了34层的网络,记为plain-34,虽然更深了,但FLOPs(代表计算复杂度,multiply-adds)仅为VGG-19的18%(毕竟VGG-19两层全连接层太耗时了);下图的右边是针对中间加入了跨层连接即残差结构,注意实线就是直接恒等变换和后面的feature map相加,虚线就是由于维度不匹配需要先升维后相加
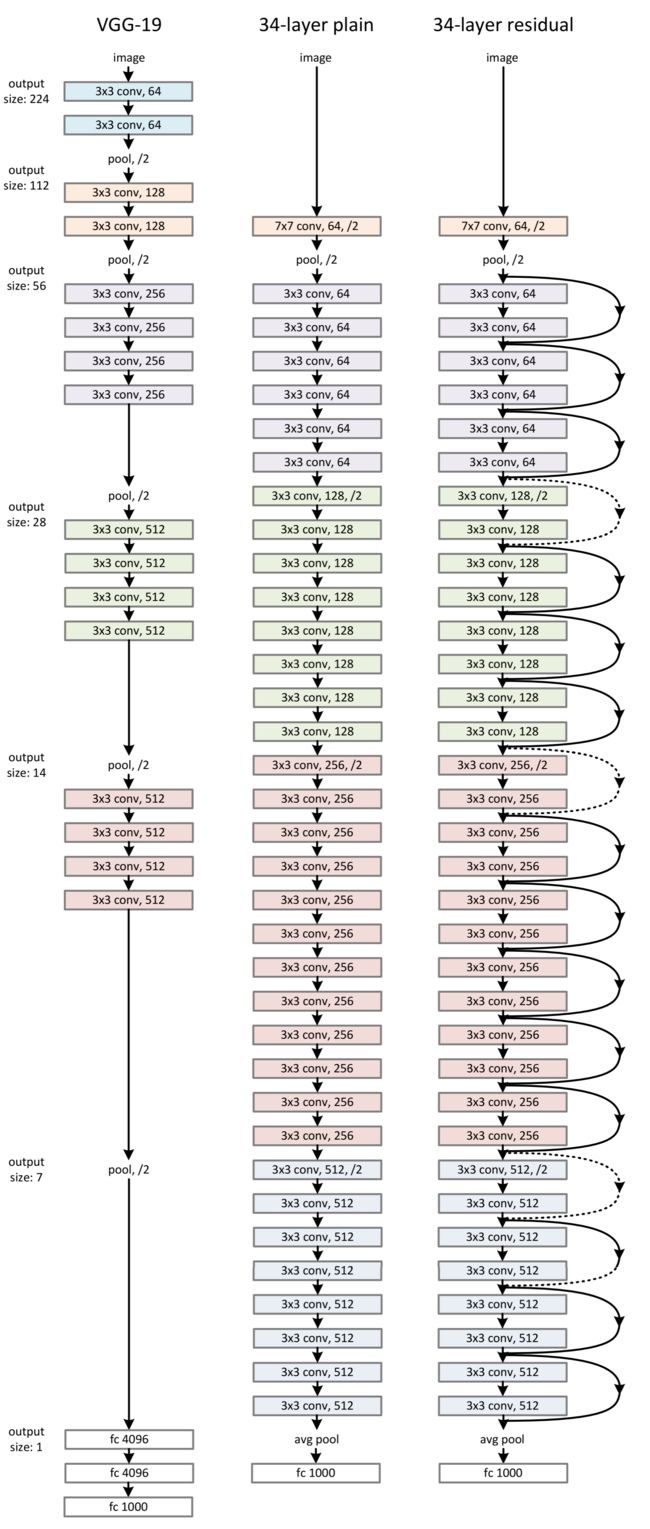
注意这里除第一个stage之外都会在stage的第一层使用步长为2的卷积来进行下采样,倒数第二层输出的feature map后面是全局平均池化(global average pooling,VGGNet预测时转化成全卷积网络的时候也用到了),也就是每个feature map求平均值,因为ImageNet输出是1000个类别,所以再连接一层1000个神经元的全连接层,最后再接上一个Softmax
再读Batch Normalization
我们在图像预处理过程中通常会对图像进行标准化处理,这样能够加速网络的收敛。可以将输入数据的范围缩放到一个合适的范围内
如下图所示,对于Conv1来说输入的就是满足某一分布的特征矩阵,但对于Conv2而言输入的feature map就不一定满足某一分布规律了(注意这里所说满足某一分布规律并不是指某一个feature map的数据要满足分布规律,理论上是指整个训练样本集所对应feature map的数据要满足分布规律)。而我们Batch Normalization的目的就是使我们的feature map满足均值为0,方差为1的分布规律
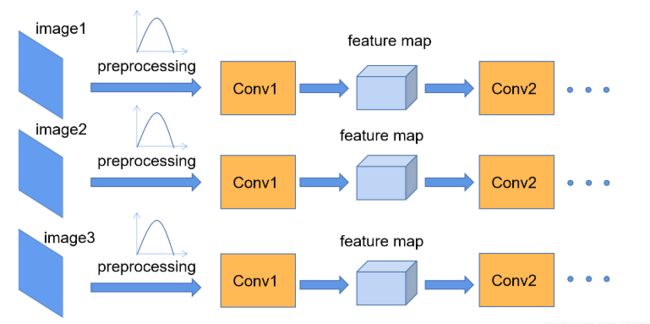

- $\mu,\sigma^2 $在正向传播过程中统计得到
- $\gamma , \beta $在反向传播过程中训练得到
Batch Normalization (BN) 是一种用于提高深度神经网络稳定性的技术,其主要目的是规范化中间特征(feature map)的分布,使其在每层具有相似的分布,从而加速训练和提高模型性能。以下是您提供信息的简化总结:
- Batch规范化原理:
- BN 的目标是使整个训练集的 feature map 满足特定分布规律。但由于直接计算整个训练集不切实际,我们使用一个 batch 的数据进行近似。批量的大小决定了近似的准确性:越大的 batch 代表的分布越接近整个数据集的分布
- 均值和方差:
- BN 中计算的均值(μB) 和方差 (σ2) 是向量而非标量。这些向量的每个元素对应于 feature map 的每个维度(通常是通道)。使用这些统计量,每个 feature map 的值被标准化
- 预测与移动平均:
- 在训练过程中,每个 batch 的均值和方差会不断变化。为了在验证和预测时获得稳定的结果,我们记录这些统计量的移动平均。在预测时,使用这些累计的平均值进行标准化
- 可学习的调整参数:
- BN 引入了两个可学习的参数:γ(用于调整方差)和 β(用于调整均值)。这些参数通过反向传播得到更新,允许模型决定最佳的数值分布规律
使用BN时需要注意的问题
- 训练时要将traning参数设置为True,在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制
- batch size尽可能设置大点,设置小后表现可能很糟糕,设置的越大求的均值和方差越接近整个训练集的均值和方差
- 建议将bn层放在卷积层(Conv)和激活层(例如Relu)之间,且卷积层不要使用偏置bias,因为没有用,参考下图推理,即使使用了偏置bias求出的结果也是一样的

迁移学习0
迁移学习是一种机器学习方法,通过将在一个任务上训练好的模型应用于另一个相关任务上,从而加速和改善模型的训练和性能。迁移学习的核心思想是,已经学习到的模型在不同的任务之间可以共享一些通用的特征表示
- 载入权重后训练所有参数
- 载入权重后只训练最后几层参数0
- 载入权重后在原网络基础上再添加一层全连接层,仅训练最后一个全连接层
为什么迁移学习有效?
- 特征通用性:在许多任务中,低级特征(如边缘、纹理等)是通用的。预训练的模型在训练时已经学习了这些通用特征,所以我们可以利用这些特征而不是从零开始
- 计算效率:使用预训练的权重可以显著减少所需的训练时间和数据量
- 防止过拟合:对于小型数据集,从零开始训练深度模型可能导致过拟合。使用迁移学习,尤其是在初步阶段冻结预训练的权重,可以有效抑制过拟合
迁移学习的常见策略:
- 特征提取:预训练模型的卷积层被用作固定的特征提取器。这些特征随后被用于训练一个新的分类器(通常是模型的全连接部分)
- 微调:除了使用预训练的权重,还可以进一步微调某些层(通常是顶层)以适应新任务。在这种方法中,通常首先冻结预训练的权重,仅训练顶部的分类器。然后解冻一些层,并使用较小的学习率继续训练
- 模型适应:对于预训练模型中的所有层,其权重都会被微调以适应新任务
注意事项:
- 学习率选择:微调时,通常对于预训练的部分使用较小的学习率,而对于新增的层使用较大的学习率。
- 数据集大小与相似性:当目标数据集很小但与预训练数据集相似时,通常只需微调顶层。当数据集较大且与预训练数据集有很大差异时,可能需要微调更多的层
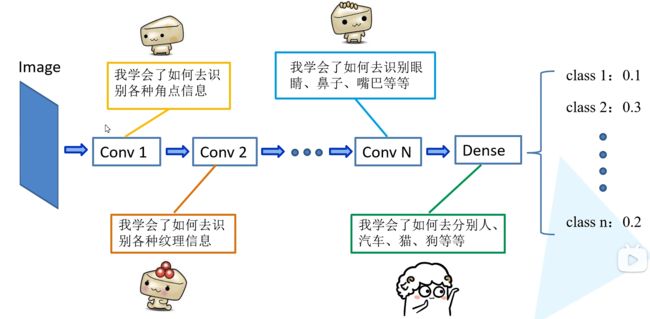
ResNet论文
- 网络深度与性能:
- ResNet 论文中的一个核心发现是:随着网络深度的增加,训练误差先是下降,然后再上升,这与传统的观点不同。这表明增加深度并不总是有益的,尤其是在没有残差连接的情况下
- 短路连接:
- 残差块的设计是为了解决深度神经网络中的梯度消失/爆炸问题。这些短路连接使得梯度可以直接反向传播到较早的层
- 不同的块设计:
- 根据输入和输出的维度是否相同,有两种类型的残差块:identity 和 convolutional。确保你理解了这两者之间的差异以及如何选择它们
- Bottleneck 架构:
- 在深层的 ResNet 版本(如 ResNet-152)中,为了提高效率,通常使用“瓶颈”设计。这种设计通过降低维度来减少每个块的计算成本
- 升维的策略:
- 在论文中,作者提出了不同的策略来处理残差块内的维度升级。确保你理解了这些方法及其之间的差异
- 权重初始化:
- 论文使用了特定的权重初始化方法(He Initialization)。这是因为,相比于其他初始化方法,它在深度残差网络中表现更好
DenseNet
问题综述
跳转到参考链接
视频-原理详解
当CNN的层数变深时,输出到输入的路径就会变得更长,这就会出现一个问题:梯度经过这么长的路径反向传播回输入的时候很可能就会消失,那有没有一种方法可以让网络又深梯度又不会消失?DenseNet提出了一种很简单的方法,DenseNet直接通过将前面所有层与后面的层建立密集连接来对特征进行重用来解决这个问题,连接方式可以看下面这张图:

DenseBlock+Transition
DenseNet的密集连接需要特征图大小一致。为了解决这个问题,DenseNet网络中使用DenseBlock+Transition的结构,其中DenseBlock是包含很多层的模块,每个层的特征图大小相同,层与层之间采用密集连接方式。而Transition模块是连接两个相邻的DenseBlock,并且通过Pooling使特征图大小降低
- DenseBlock

出于减少参数的目的,一般会先加一个1x1的卷积来减少参数量.所以我们的非线性组合函数就变成了BN+ReLU+1x1 Conv+BN+ReLU+3x3 Conv的结构
- Transition

它主要是连接两个相邻的DenseBlock,并且降低特征图大小。Transition层包括一个1x1的卷积和2x2的AvgPooling,结构为BN+ReLU+1x1 Conv+2x2 AvgPooling,也就是下采样,压缩模型的功能.假定上一层得到的feature map的channel大小为m,那经过Transition层就可以产生 θ m \theta m θm个特征,其中 θ \theta θ是0和1之间的压缩系数
整个结构的计算:

DenseNet:

DenseNet特点
- 缓解梯度消失问题:由于层与层之间的直接连接,前面层的梯度可以直接传递到后面的层,从而缓解深层网络中的梯度消失问题
- 增强特征传播:直接连接多个层可以更好地将前面层的信息传递到后续层,从而改进整体的信息流和梯度传播
- 促进特征再用:密集连接保留了从网络的早期阶段传来的低维度特征,从而使得特征可以在网络中得到重复利用
- 参数效率高:由于特征的重复利用,网络不需要重新学习冗余的特征,从而减少了模型的参数数量并提高了计算效率
- 自带正则化效果:密集连接的结构提供了一种内在的正则化,有助于减少过拟合,尤其是在数据量较小的情况下
SeNet
问题综述
Squeeze-and-Excitation Network
跳转到参考链接
视频-原理详解
- CNN的核心:CNN网络主要通过卷积算子完成特征提取,使用卷积核将输入特征图转化为新的特征图
- 卷积的本质:对局部区域进行特征融合,这涉及到空间上的特征融合(W和H维度)以及通道间的特征融合(C维度)。大部分的卷积操作都旨在扩大感受野,融合更多的空间特征,或提取多尺度的空间信息
- SENet的核心创新:SENet关注的是不同通道(channel)之间的关系,通过学习每个通道特征的重要性来自动调整它们
- SE模块的中心思想:为每个输出通道预测一个权重,然后对每个通道进行加权。这在本质上是在通道维度上进行了注意力或门控操作,允许模型更加关注于那些包含更多信息的通道,同时减少对那些不重要的通道的依赖
- SENet的优点:可以轻松地整合到现有网络中以增强其性能,同时带来的计算代价很小
简而言之,SENet通过引入注意力机制,允许模型在通道维度上自适应地加权特征,从而优化模型性能
如下就是 SENet的基本结构:

Squeeze+Excitation
SENet中的"Squeeze-and-Excitation"(SE)模块的核心是对不同的通道进行权重调整,以突出更为重要的特征通道。以下是从图像输入到SE模块输出的完整过程:
前期特征提取:首先,原始图像通过一系列卷积层,池化层,激活函数等进行特征提取。这部分不是SE模块的一部分,但为了完整性,我们提及它。输出的结果是一个多通道的特征图
Squeeze操作:
- 全局平均池化:为了从每个通道获取全局信息,对特征图执行全局平均池化。对于每个通道,这会压缩所有的空间信息,输出一个标量,代表该通道的平均响应。假设有C个通道,那么输出将是一个C维的向量

Excitation操作:
- 第一全连接层(降维):该C维向量经过一个全连接层(FC层),其输出维度是C/r,其中r是一个降维的比例(常见的值如16)。这一层通常使用ReLU作为激活函数
- 第二全连接层(升维):经过降维处理的特征向量再经过另一个全连接层,其输出维度恢复为C。这一层使用sigmoid作为激活函数,确保输出值在0到1之间

重新加权特征图:使用Excitation操作产生的C维权重向量(每个值都在0到1之间)来按元素乘以原始特征图的每个通道。这基本上是对原始特征图每个通道进行重新加权,强化模型认为更重要的通道,抑制那些不那么重要的通道
简而言之,SE模块的主要思想是使用全局信息(Squeeze操作)来自适应地重新加权各个通道(Excitation操作),从而提高模型对重要特征的关注度
注意一下表述:
SENet中的Squeeze-and-Excitation模块通过捕获通道间的关系为每个特征通道重新分配权重,强调了注意力机制的概念。以下是一个简化的总结:
Squeeze操作:通过全局平均池化从多通道特征图中获得一个C维向量,这反映了每个通道的全局响应
Excitation操作:
- 非线性变换:为了捕捉通道之间的关系,使用两个全连接层进行非线性变换
- 降维与恢复:首先,通过一个全连接层将C维向量降维到C/r(其中r是超参数)。这一层使用ReLU激活函数
- 重新加权:接着,将C/r维向量通过另一个全连接层恢复为C维,并使用sigmoid激活函数,确保得到的权重在0到1之间
重标定:使用Excitation操作得到的权重向量逐通道地乘以原始的特征图,实现在通道维度上的重标定
本质上,SE模块可以看作是一种注意力机制,它计算出一个权重系数,强调或减弱原始特征图的某些通道,使得模型能够更专注于那些更为重要的特征
SE-Inception+SE-ResNet
ResNet论文
更深的网络反而更容易训练的现象是由于残差结构(如ResNet中的残差块)的引入所产生的。这种现象可以通过深度网络的梯度传播和特征重用等方面来解释:
- 梯度传播的改善:深度网络中的梯度消失和梯度爆炸问题是训练深层网络时的常见难题。但是,通过引入残差连接,梯度在跳跃连接中可以直接传播,无论网络多深,梯度都能够相对稳定地传递到较浅的层。这使得训练更深的网络变得更加容易,因为更深的网络可以更好地利用梯度信息。
- 特征重用:更深的网络可以更好地利用特征重用的优势。在残差块中,恒等映射(identity mapping)允许特征可以直接传递到下一层,从而被后续层重复使用。这有助于网络在更深的层次上学习到更多高级的抽象特征,从而提高了网络的表达能力。
- 网络表示能力:更深的网络通常具有更强大的表示能力,可以学习到更复杂、更多样的特征模式。这使得网络能够更好地适应各种复杂的任务。
- 非线性建模:更深的网络可以更好地进行非线性建模,因为每个残差块都包含一个非线性变换。这允许网络更好地适应数据中的复杂关系。
MobileNet
MobileNet介绍
Efficient Convolutional Neural Networks for Mobile Vision Applications
跳转到参考链接
视频-原理详解
- MobileNet是专门为了移动端和嵌入式深度学习应用设计的网络结构,主要是为了得到一个在较低配置资源上也具有非常好的效果的这个特性
- MobileNet一种高效的网络架构和一组两个超参数,以建立非常小、低延迟的模型,可以很容易地匹配移动和嵌入式视觉应用程序的设计需求
- 其主要特点为:轻量化和直接使用stride=2的卷积代替池化层
深度可分离卷积
**其主要创新点:**引入了depthwise separable convolutions(深度可分离卷积),主要分解为两个更小的卷积操作:depthwise convolutions(深度卷积)和pointwise convolutions(逐点卷积),其主要目的是降低参数量和计算量
深度可分离卷积

DW结构
缺点:卷积核参数大部分为零

PW结构
计算量对比

输入特征图(DF,DF,M),输出特征图为(DG,DG,N)。标准卷积核为(DK,DK,M,N),将标准卷积分解为深度卷积和逐点卷积;其中深度卷积负责滤波作用(基于输入的feature map提取更高阶的特征),核大小为(DK,DK,1,1),总共有M个核;逐点卷积负责转换通道(合并之前的高阶特征信息,形成最终的feature map),核大小为(1,1,M,N)
- 标准卷积计算过程:
D K ⋅ D K ⋅ M ⋅ D G ⋅ D G ⋅ N D_{K}\cdot D_{K}\cdot M\cdot D_{G}\cdot D_{G}\cdot N DK⋅DK⋅M⋅DG⋅DG⋅N
- MobileNet计算过程:
- 深度卷积
D κ ⋅ D κ ⋅ D G ⋅ D G ⋅ M D_{\kappa}\cdot D_{\kappa}\cdot D_{G}\cdot D_{G}\cdot M Dκ⋅Dκ⋅DG⋅DG⋅M
- 逐点卷积
M ⋅ D G ⋅ D G ⋅ N M\cdot D_{G}\cdot D_{G}\cdot N M⋅DG⋅DG⋅N
M ⋅ D G ⋅ D G ⋅ N + D K ⋅ D K ⋅ D G ⋅ D G ⋅ M D K ⋅ D K ⋅ M ⋅ D G ⋅ D G ⋅ N = 1 D K 2 + 1 N \frac{M\cdot D_{G}\cdot D_{G}\cdot N+D_{K}\cdot D_{K}\cdot D_{G}\cdot D_{G}\cdot M}{D_{K}\cdot D_{K}\cdot M\cdot D_{G}\cdot D_{G}\cdot N}=\frac{1}{D_{K}^{2}}+\frac{1}{N} DK⋅DK⋅M⋅DG⋅DG⋅NM⋅DG⋅DG⋅N+DK⋅DK⋅DG⋅DG⋅M=DK21+N1
由此可见计算量大幅降低
两个超参数
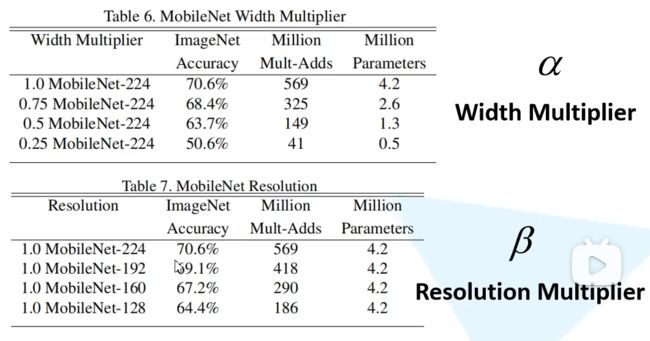
宽度因子α
引入第一个控制模型大小的超参数:宽度因子α(Width Multiplier),用于控制输入和输出的通道数,即将输入通道从M变成αM,输出通道从N变成αN。α的一般取值为:[1.0, 0.75, 0.5, 0.25]
NOTE: 计算量和参数量减低了约α^2倍D K ⋅ D K ⋅ D G ⋅ D G ⋅ α M + α M ⋅ D G ⋅ D G ⋅ α N D K ⋅ D K ⋅ M ⋅ D G ⋅ D G ⋅ N = α N + α 2 D K 2 \frac{D_{K}\cdot D_{K}\cdot D_{G}\cdot D_{G}\cdot\alpha M+\alpha M\cdot D_{G}\cdot D_{G}\cdot\alpha N}{D_{K}\cdot D_{K}\cdot M\cdot D_{G}\cdot D_{G}\cdot N}=\frac{\alpha}{N}+\frac{\alpha^{2}}{D_{K}^{2}} DK⋅DK⋅M⋅DG⋅DG⋅NDK⋅DK⋅DG⋅DG⋅αM+αM⋅DG⋅DG⋅αN=Nα+DK2α2
分辨率因子ρ
引入第二个模型大小控制参数:分辨率因子ρ(Resolution Multiplier),用于控制输入和内部层的表示,即输出层的分辨率控制。常见输入通道为224,192,160和128,ρ取值范围一般(0,1]
D K ⋅ D K ⋅ ρ D G ⋅ ρ D G ⋅ α M + α M ⋅ ρ D G ⋅ ρ D G ⋅ α N D K ⋅ D K ⋅ M ⋅ D G ⋅ D G ⋅ N = α ρ 2 N + α 2 ρ 2 D K 2 \frac{D_K\cdot D_K\cdot\rho D_G\cdot\rho D_G\cdot\alpha M+\alpha M\cdot\rho D_G\cdot\rho D_G\cdot\alpha N}{D_K\cdot D_K\cdot M\cdot D_G\cdot D_G\cdot N}=\frac{\alpha\rho^2}{N}+\frac{\alpha^2\rho^2}{D_K^2} DK⋅DK⋅M⋅DG⋅DG⋅NDK⋅DK⋅ρDG⋅ρDG⋅αM+αM⋅ρDG⋅ρDG⋅αN=Nαρ2+DK2α2ρ2
MobileNetV2
- 倒残差结构

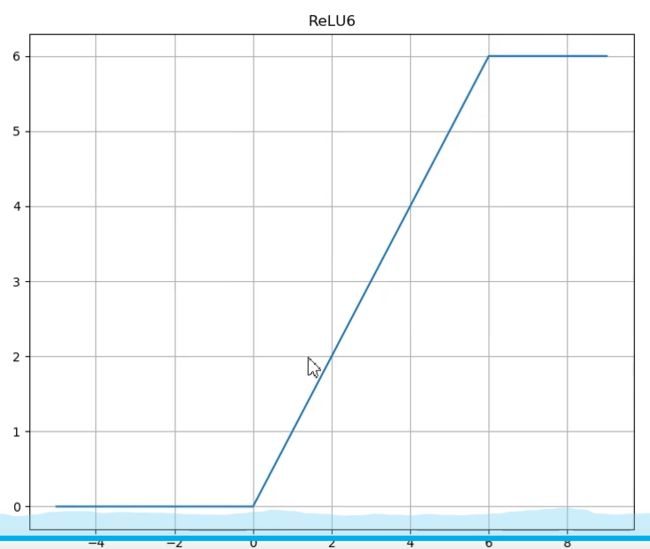
- ReLU
- ReLU激活函数对低维特征信息信息造成较大损失
- 两边大中间小,因此需要使用Linear避免信息损失
- bottleneck

当stride=1且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接

- 参数

- t是扩展因子
- c是输出特征矩阵深度channel
- n是bottleneck的重复次数
- s是步距 (针对第一层,其他为1)
MobileNetV3
- 模块位置:
- 在MobileNetV3中,注意力机制(SE)被引入到网络的特定层,以增强通道之间的关系。它在网络中的特定位置应用,并不是每个层都使用。
- 在SENet中,通道注意力模块被嵌入到每个残差块中。这意味着在SENet的每个残差块内都会进行通道注意力的计算,以影响每个块的特征图。
- 目标:
- MobileNetV3的主要目标是构建轻量级的网络,适用于计算资源受限的场景下。注意力机制(SE)被用来增强通道间的关系,以提高网络的性能。
- SENet的主要目标是通过加强通道注意力,提高深度网络的表达能力。它的设计更加专注于解决深层网络中的问题

- 加入SE模块
- 更新激活函数,NL表示函数不确定
- 注意力机制(SE)

- 重新设计耗时结构
- 减少第一个卷积层的卷积个数(32->16)
- 精简Last Stage

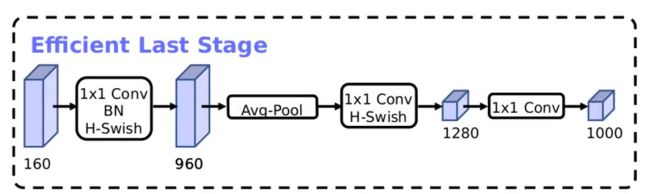
- 重新设计激活函数

σ ( x ) = 1 1 + e − x ReLU6 ( x ) = min ( max ( x , 0 ) , 6 ) h - sigmoid = ReLU6 ( x + 3 ) 6 \begin{gathered} \sigma(x)=\frac{1}{1+e^{-x}} \\ \operatorname{ReLU6}(x)=\min(\max(x,0),6) \\ \text{h - sigmoid}=\frac{\text{ReLU6}(x+3)}{6} \end{gathered} σ(x)=1+e−x1ReLU6(x)=min(max(x,0),6)h - sigmoid=6ReLU6(x+3)
swish x = x ⋅ σ ( x ) \operatorname{swish}x=x\cdot\sigma(x) swishx=x⋅σ(x)
h - swish = x ReLU6 ( x + 3 ) 6 \text{h - swish}=x\frac{\text{ReLU6}(x+3)}{6} h - swish=x6ReLU6(x+3)
- 参数(MobilNetFV3-Large)

- groups
分组卷积是一种特殊的卷积操作,将输入通道分组并为每组分配卷积核。这降低了计算量,提高了效率。分组卷积的优点是减少卷积核数量、计算量,并增强非线性能力
ShuffleNet
ShuffleNetV1
跳转到参考链接
视频-原理详解
ShuffleNet是一种满足在受限条件下的高效基础网络结构,基于分组卷积(Group Convolution)和深度可分离卷积(Depthwise SeparableConvolution)
- 分组卷积
简单的分组卷积会导致每个卷积操作仅从某些部分的输入通道数据中导出,会降低通道之间的信息流通,降低信息的表达能力,故在做Group Convolution之前先做一个channel的shuffle操作,以保障信息的表达能力

shuffle
对于channel的shuffle操作,一般采用如下操作:
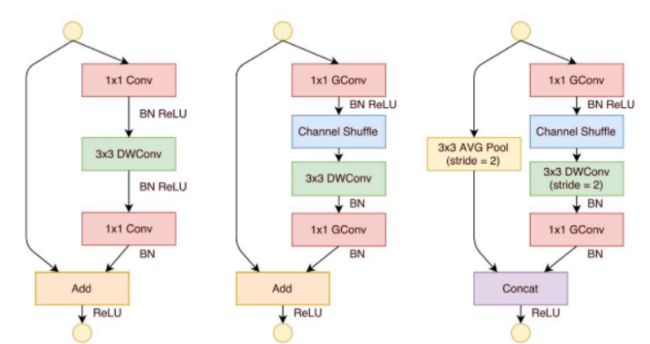
- 中间为stride=1,右边stride=2
- 注意Add与Concat
- 参数
第一个不使用Gconv
ShuffleNetV2
FLOPS:全大写,指每秒浮点运算次数,可以理解为计算的速度。是衡量硬件性能的一个指标
FLOPs:s小写,指浮点运算数,理解为计算量。可以用来衡量算法/模型的复杂度。(模型)在论文中常用GFLOPs(1GFLOPs = 109 FLOPs )

- 运行速度是最直接的指标
- FLOPs仅仅考虑卷积的计算量
高效网络架构设计的几个实用指南
- 等通道宽度可最大限度地降低内存访问成本(MAC)
当卷积层的输入特征矩阵与输出特征矩阵channel相等时MAC最小(保持FLOPs不变时)
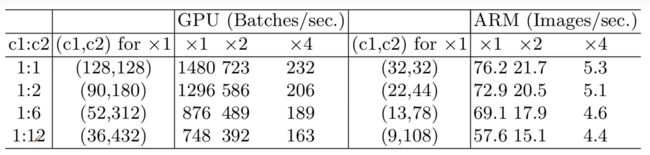
- 过多的组卷积增加MAC(保持FLOPs不变时)

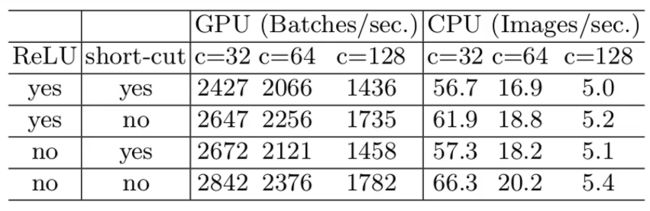
利用上述原则进行设计

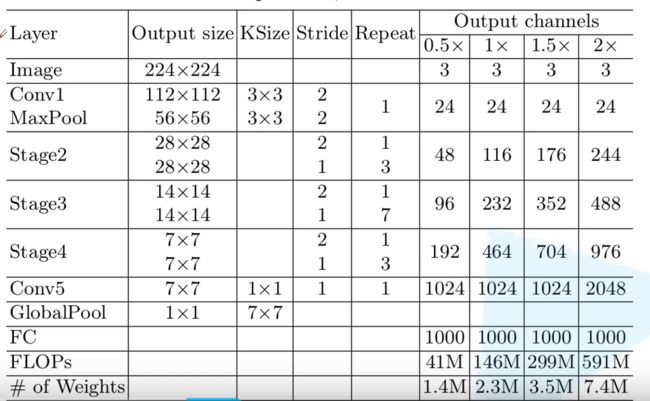
多了一个Conv5
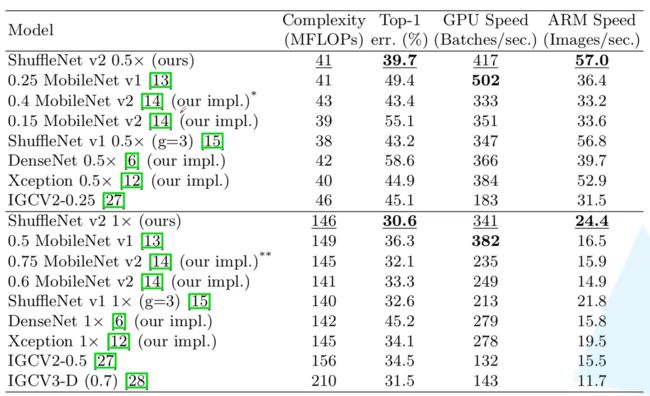
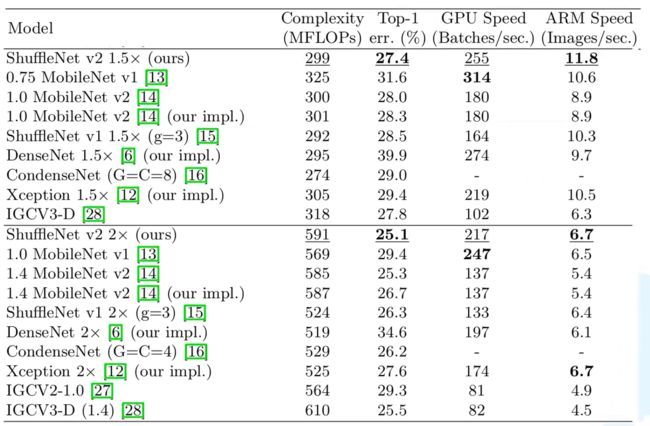
RepVGG
问题综述
早期卷积网络结构主要是手工设计,通过不断堆叠卷积层以取得更好的效果(如AlexNet和VGG)
多分支结构
第一次出现多分支结构应该是在Inception中,就获得了高性能收益,加上不同分支应用不同卷积核,能获得不同感受野,后续出现的ResNet,其残差结构也是多路结构。但是需要注意的是:多路结构需要保存中间结果,显存占有量会明显增高,只有到多路融合时,显存会会降低
同时,由ShuffleNet论文中提到的网络高效推理法则:模型分支越少,速度越快。所以,可想而知,多分支结果虽然会带来高性能收益,但是,显存占用明显增加,且模型推理速度会一定程度降低,这在工业场景上是不实用的
- 性能优异组件
随着不断尝试于探索,出现了很多性能优异的网络组件,比如深度可分离卷积,分组卷积等等,这些都可以显著增加网络性能,但是,我们也知道,就拿group conv来说,当group越多是,我们知道网络性能会越好,但是,其MAC(内存访问成本)也会显著增大,最终导致模型变慢,深度可分离卷积虽然可以显著降低FLOPs,但是其MAC也会增加,最终导致模型速度变慢
这就引发了一个矛盾,既然多分支结构和性能优异的组件能显著提高模型性能,但是,又会最终导致模型在推理时速度变慢且还非常耗内存。这种问题该怎么解决呢?
repVGG绝对可以算得上2020年在backbone方面有很大影响力的工作,其核心思想是:通过结构重参数化思想,让训练网络的多路结构(多分支模型训练时的优势——性能高)转换为推理网络的单路结构(模型推理时的好处——速度快、省内存)),结构中均为3x3的卷积核,同时,计算库(如CuDNN,Intel MKL)和硬件针对3x3卷积有深度的优化,最终可以使网络有着高效的推理速率
选择VGG网络的原因
速度快
现有的计算库(如CuDNN,Intel MKL)和硬件针对3x3卷积有深度的优化,相比其他卷积核,3x3卷积计算密度更高,更加有效
节省显存
因为各个分支的结果需要保存,直到最后一步融合(比如add),才能把各分支显存释放掉
以残差块结构为例子,它有2个分支,其中主分支经过卷积层,假设前后张量维度相同,我们认为是一份显存消耗,另外一个旁路分支需要保存初始的输入结果,同样也是一份显存消耗,这样在运行的时候是占用了两份显存,直到最后一步将两个分支结果Add,显存才恢复成一份。而Plain结构只有一个主分支,所以其显存占用一直是一份
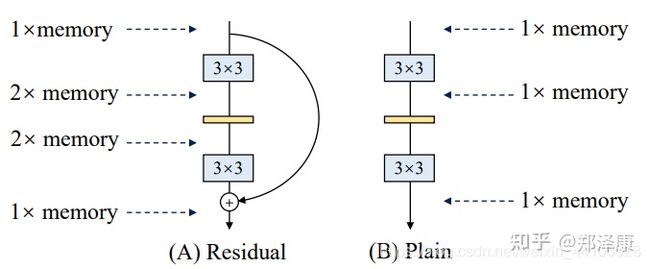
灵活性好
多分支结构会引入网络结构的约束,比如Resnet的残差结构要求输入和卷积出来的张量维度要一致(这样才能相加),这种约束导致网络不易延伸拓展,也一定程度限制了通道剪枝。对应的单路结构就比较友好,剪枝后也能得到很好的加速比
RepVGG主体结构

受Resnet的残差结构启发,我们引入了残差分支和1x1卷积分支,为了后续重参数化成单路结构,我们调整了分支放置的位置,没有进行跨层连接,而是直接连了过去
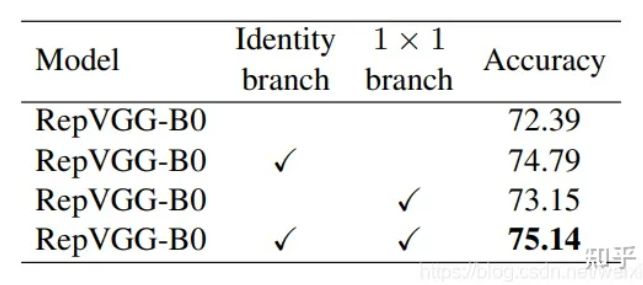
其中Idendity分支(即残差连接)提升尤为明显,1x1卷积分支也能提供近一个点的贡献。两个分支合并能贡献3个点的提升
相当于一个Block内所作的计算为
Out = F ( X ) + G ( X ) + X F ( X ) 表示 3 ∗ 3 卷积 G ( X ) 表示1 ∗ 1 卷积 \begin{gathered} \text{Out} =F(X)+G(X)+X \\ F(X)\text{表示}3*3\text{卷积} \\ G(X)\text{表示1}*1\text{卷积} \end{gathered} Out=F(X)+G(X)+XF(X)表示3∗3卷积G(X)表示1∗1卷积
多分支融合技术
卷积层和BN层合并


RepVGG中卷积层没有使用Bias
3x3卷积和1x1卷积融合
1x1卷积不需要padding,就能保证特征图大小前后一致
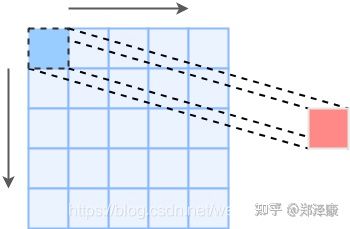
3x3为了保证特征图大小不变,我们需要在原特征图上padding一圈
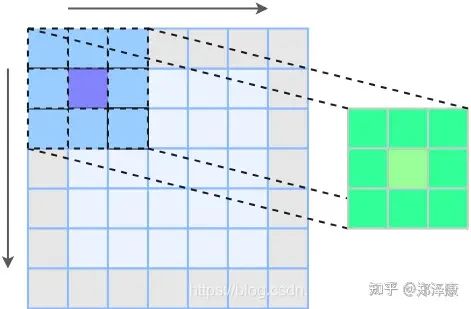
我们观察下3x3卷积核中间的那个核,会惊奇的发现它卷积的路径就是前面1x1卷积的路径


identity分支等效特殊权重
现在的问题是将identity分支用一个卷积层表示,这样才有可能融合。identity前后值不变,那么我会想到是用权重等于1的卷积核,并分开通道进行卷积,即1x1的,权重固定为1的Depthwise卷积。这样相当于单独对每个通道的每个元素乘1,然后再输出来,这就是我们想要的identity操作!下面是一个示意图
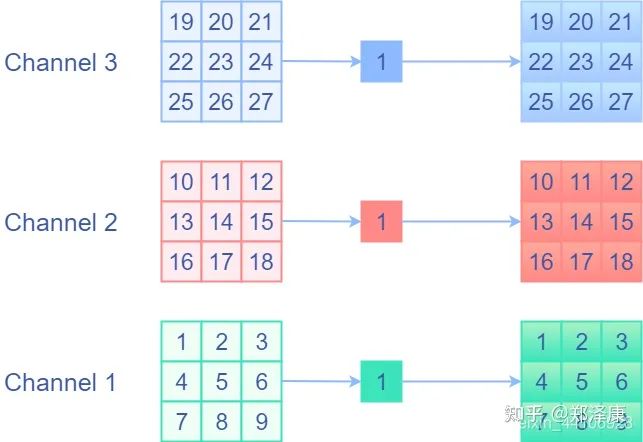
融合最终结构
深层卷积
新的问题产生了,我们的3x3和1x1分支都不是Depthwise卷积,现在也是不能融合进去的,我们需要把Depthwise卷积以普通卷积的形式表达出来。
因为普通卷积输出是将各个通道结果相加,那么自然而然想到,我们只要将当前通道对应的卷积权重设置为1,而其他通道权重设置为0,不就等价Depthwise卷积了! 下面是一个示意图
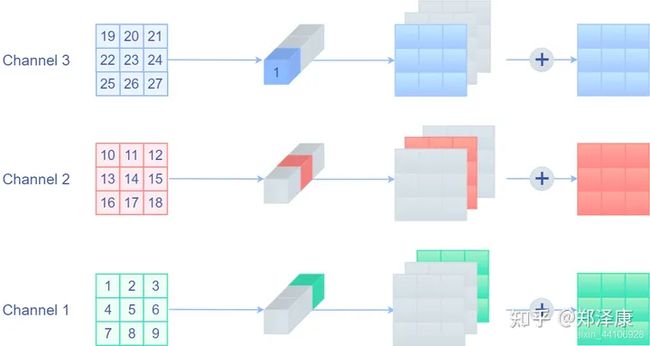
其中灰色的地方均表示0
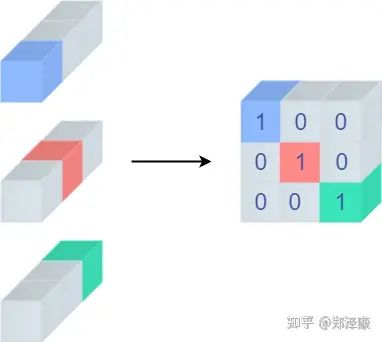
MobileOne
问题综述
MobileOne 模型本身没有特别新颖的创新点,可以看作一个 MobileNet、 重参数技术、训练技巧的组合创新成果。MobileOne使用的过参数化(Over-parametrization)。我们的经验是:MobileOne的结构不一定是最好用的,但基于过参数化的重参数化大概率能涨点
MobileOne创新点:
- 使用了过参数化
- 使用了与MobileNet类似的深度可分离卷积结构
- 3 个特有的训练优化技巧
- 渐进式学习策略
- 退火权重衰减系数
- 指数平均移动 EMA
过参数化
过参数化(Over-parametrization)

左图是一个普通Conv-BN-Act模块,其中Act是激活函数。图1中右图是过参数化示意图,它使用了M个相同的并行分支,然后将所有分支的输出相加后再进激活函数
重参数化:
- 一个Conv和一个BN可以被合并为一个Conv
- 对于多个超参数(如核大小、步长、padding等)相同的Conv,如果它们的输出是直接相加,那么这些Conv可以合并为一个新的Conv
所以对于图1中的过参数化模块,当训练结束后,可以首先将每一条Conv-BN分支合并为一个Conv,然后将合并后的所有Conv再合并为一个新的Conv。那么过参数化模块在推理阶段实际只包含一个Conv和一个Act.了,与图1中左边的结构等价(左边的Conv和BN也可重参数化)。上述过程如2图所示
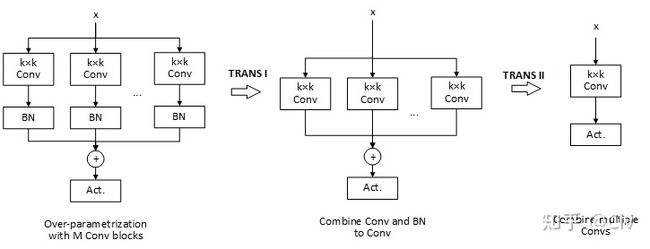
重参数化方法一:卷积层与BN层的合并;重参数化方法二:多分支相加
图1中的过参数化方法能够在保持相同推理结构的基础上,增加在训练时模型的复杂度。这是过参数化具有增益的主要原因
building block
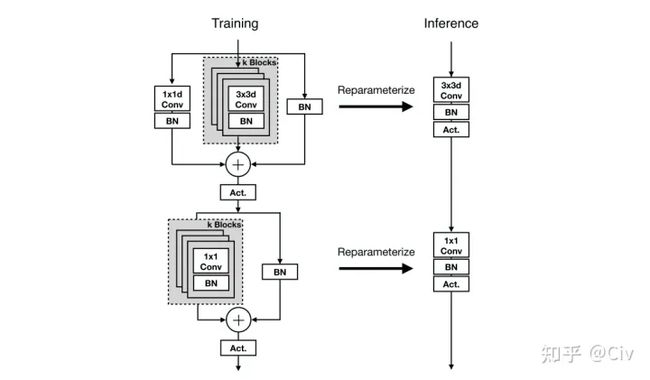
图3中的左侧部分构成了MobileOne的一个完整building block。它由上下两部分构成,其中上面部分基于深度卷积(Depthwise Convolution),下面部分基于点卷积(Pointwise Convolution)
深度卷积与点卷积的术语来自于MobileNet。深度卷积本质上是一个分组卷积,它的分组数g与输入通道相同。而点卷积是一个1×1卷积
深度卷积:
图中的深度卷积模块由三条分支构成。最左侧分支是1×1卷积;中间分支是过参数化的3×3卷积,即k个3×3卷积;右侧部分是一个包含BN层的跳跃连接。这里的1×1卷积和3×3卷积都是深度卷积(也即分组卷积,分组数g等于输入通道数)
点卷积:
图中的点卷积模块由两条分支构成。左侧分支是过参数化的1×1卷积,由k个1×1卷积构成。右侧分支是一个包含BN层的跳跃连接
在训练阶段,MobileOne就是由这样的building block堆叠而成
当训练完成后,可以使用重参数化方法将图3中左侧所示的building block重参数化图3中右侧的结构(实际上右侧的BN也应该去掉,此图为论文原图,应该有误)。以图3中的深度卷积部分为例,介绍它的重参数化过程
假设深度卷积部分的输入通道为d,那么深度卷积的分组数也为d
- 对于左侧的1×1卷积分支,将1×1卷积和BN使用**重参数化方法一(卷积层与BN层的合并)**合并为一个分组数也为d的1×1卷积,将该卷积记为A
- 对于中间的过参数化3×3卷积分支,对每一个单独的3×3卷积,将3×3卷积与它的BN使用**重参数化方法一(卷积层与BN层的合并)合并为一个分组数为d的3×3卷积。由此得到K个3×3卷积。然后使用重参数化方法二(多分支相加)**将这K个3×3卷积合并为一个卷积,将该卷积记为B
- 对于右侧的跳跃连接,我们首先人为在BN层之前添加一个卷积,该卷积的参数人为设定,它需要满足对于任意输入x,经过该卷积后输出也为x。这样的卷积称为Dirac delta,有了Dirac delta卷积,就可以再使用**重参数化方法一(卷积层与BN层的合并)**将它与BN层合并,得到一个新的3×3卷积,将该卷积记为C(注:将Dirac delta设置为3×3来确保这里得到的也是3×3;Dirac delta的分组数也需要设置为d)
- 使用**重参数化方法六:多尺度卷积**将上述三个得到的新卷积A、B、C合并为一个新卷积。新卷积的分组数也为d,如图3中右侧上半部分所示(由此可知此处BN实际不存在)
至此完成了对深度卷积部分的重参数化。点卷积部分类似,不再赘述
训练优化技巧
渐进式学习策略:EfficientNetV2引入的方法,逐步增大图像大小,同时采用更强的正则化(如数据增强和dropout)策略,以提高训练效果。在37轮和112轮时,增加图像分辨率和AutoAug的强度,加快训练速度并提升模型精度
退火权重衰减系数:针对小型模型,需要较少的正则化以防止过拟合。在训练早期,通过对权重正则化(Weight-Decay)引起的损失进行退火处理,比消除权重正则化更有效
指数平均移动:深度学习中常用的训练技巧,用于加强模型的稳定性和泛化能力。指数平均移动(EMA)可被视为一种集成方法,将训练过程中的权重进行集成,用简单的公式实现,有助于提升模型性能
FasterNet
问题综述
为了设计快速神经网络,许多工作都集中在减少浮点运算的数量(FLOPs)上。目前 FLOPs,在许多经典的工作中都指的是 multiply-adds,即:一次乘法和一次加法这个整体的数量。而,我们观察到FLOPs的减少并不一定会导致延迟的类似程度的减少。但是这些操作在带来 FLOPs 减小的过程中还会带来另一种副作用,即:内存访问 (memory access) 的增加。而且,以上这些模型通常伴随着额外的数据操作,如拼接 (concatenation), 打乱 (shuffling), 和池化 (pooling),其运行时间对于小模型往往是显著的
这主要源于低效率的每秒浮点运算(FLOPS)。 为了实现更快的网络,我们回顾了流行的操作,并证明如此低的FLOPS主要是由于操作频繁的内存访问,特别是深度卷积。 因此,我们提出了一种新的部分卷积(PConv),通过同时减少冗余计算和内存访问,可以更有效地提取空间特征
部分卷积
- 部分卷积 PConv 的设计
本文给出的解决方案部分卷积 (Partial Convolution, PConv) 的出发点是卷积神经网络特征的冗余性。如下图所示是在预训练的 ResNet50 的中间层中可视化特征图,左上角的图像是输入,特征图在不同通道之间具有很高的相似性

部分卷积设计的目的是同时减小内存访问和计算冗余,其和常规卷积,DWConv 的区别如下图3所示,工作原理如下图所示

PConv 对部分输入通道应用常规的 Conv 来进行空间特征提取,而对其余通道保持不变
FasterNet网络

鉴于新型PConv和现成的PWConv作为主要的算子,进一步提出FasterNet,这是一个新的神经网络家族,运行速度非常快,对许多视觉任务非常有效。作者的目标是使体系结构尽可能简单,使其总体上对硬件友好
在图中展示了整体架构。它有4个层次级,每个层次级前面都有一个嵌入层(步长为4的常规4×4卷积)或一个合并层(步长为2的常规2×2卷积),用于空间下采样和通道数量扩展。每个阶段都有一堆FasterNet块。作者观察到,最后两个阶段中的块消耗更少的内存访问,并且倾向于具有更高的FLOPS。因此,放置了更多FasterNet块,并相应地将更多计算分配给最后两个阶段。每个FasterNet块有一个PConv层,后跟2个PWConv(或Conv 1×1)层。它们一起显示为倒置残差块,其中中间层具有扩展的通道数量,并且放置了Shorcut以重用输入特征
除了上述算子,标准化和激活层对于高性能神经网络也是不可或缺的。然而,许多先前的工作在整个网络中过度使用这些层,这可能会限制特征多样性,从而损害性能。它还可以降低整体计算速度。相比之下,只将它们放在每个中间PWConv之后,以保持特征多样性并实现较低的延迟
此外,使用批次归一化(BN)代替其他替代方法。BN的优点是,它可以合并到其相邻的Conv层中,以便更快地进行推断,同时与其他层一样有效。对于激活层,根据经验选择了GELU用于较小的FasterNet变体,而ReLU用于较大的FasterNet变体,同时考虑了运行时间和有效性。最后三个层,即全局平均池化、卷积1×1和全连接层,一起用于特征转换和分类
为了在不同的计算预算下提供广泛的应用,提供FasterNet的Tiny模型、Small模型、Medium模型和Big模型变体,分别称为FasterNetT0/1/2、FasterNet-S、FasterNet-M和FasterNet-L。它们具有相似的结构,但深度和宽度不同
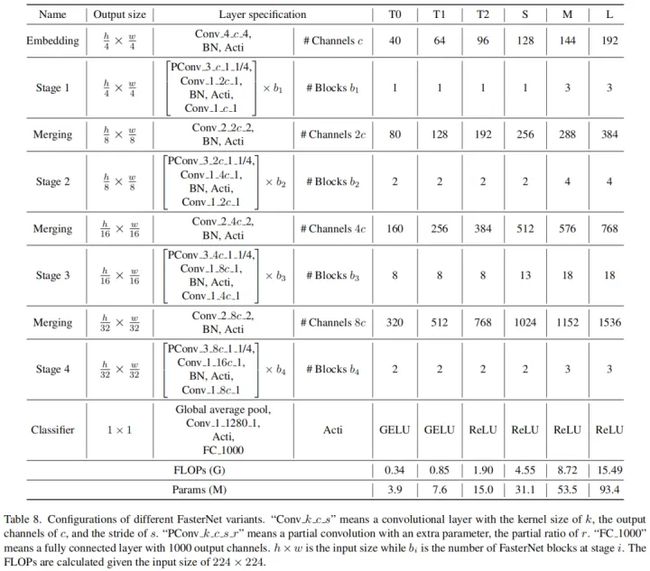
[跳转到开头](#卷积神经网络(Convolutional Neural Networks,CNN))
学习复现重点
- AlexNet
- VGG
- ResNet
- MobileNet
区域卷积神经网络(Regions with CNN features,R-CNN)
文章目录
- 前言
-
- Stacking(堆叠)
- 深度学习/神经网络
- **深度神经网络**(Deep Neural Networks,DNN)
-
- 几个重要问题
-
- 深度学习和神经网络的关系
- 什么是神经网络
- 神经网络如何进行学习
-
- 向量化操作
- 损失函数
- 学习率退火(learning rate annealing)
- 为什么神经网络用到梯度下降优化方法
- 梯度消失和梯度爆炸
-
- 梯度消失和梯度爆炸
- 梯度消失、爆炸的解决方案
-
- 预训练和微调
- 梯度剪切、正则
- relu、leakyrelu、elu等激活函数
- Batch Normalization(批规范化)
- 残差结构
- 深度神经网络定义
- 单个神经元的计算
-
- Step1 累加求和
- Step2 激活
- 神经元在神经网络中的计算
- 反向传播算法内容
-
- Step1 计算误差
- Step2 更新权重
- 具体实例
-
- 实例简单理解
- 示例详解
-
- 下面是前向(前馈)运算
- 下面是反向传播
- 参数更新过程
- 误差E对w1的导数
- 卷积神经网络(Convolutional Neural Networks,CNN)
-
- 目录
- 参考链接
- 卷积运算
- 卷积背后的直觉
- 卷积神经网络的层级结构
-
- 输入层(Input layer)
- 卷积层(CONV layer)
-
- 卷积层的作用
- 神经元的空间排列
-
- 深度(depth)
- 步长(stride)
- 填充(padding)
- 几种不同卷积简介
-
- 扩张卷积 (Dilated Convolution)
- 分组卷积
- 深度可分离卷积
- 池化层(Pooling layer)
-
- 池化层作用
- 池化层分类
- 池化层特点
- 感受野
-
- 感受野介绍
- 感受野计算
- 计算实例
- 卷积神经网络中的不变性
- 非线性映射函数
-
- 激活函数作用
- 几种激活函数
-
- Sigmoid激活函数
- Tanh激活函数
- ReLU
- 激励层建议
- 优化器
- 通用矩阵乘(GEMM)
- Flatten层与全连接层(FC layer)
- 全连接与卷积转换
-
- 将卷积层转化成全连接层
- 将全连接层转化成卷积层
- 参数初始化
- 归一化
-
- 内部协变量偏移
- 几种归一化展示
- 批归一化
-
- 具体步骤
- 优缺点
- 层归一化
- 实例归一化
- 组归一化
- 自适应的归一化
- 正则化与Dropout
-
- 正则化
- Drpout
- Vanilla Dropout与Inverted Dropout
- Dropout 和 DropBlock
- 权重衰减(weight decay)
- 适用
- 卷积神经网络的训练
-
- 卷积网络示意图
- 单层卷积层
-
- 卷积的导数及反向传播
- 多通道
- 使⽤ GEMM 转换
- 单层池化层
-
- 池化的导数及后向传播
- 上采样
- 数据增强
-
- 翻转(Flip)
- 随机裁剪(crop采样)
- fancy PCA
- 样本不均衡
- 其余数据增强方式
- 训练和测试间的协调
- 超参数的调节
-
- 学习率(Learning Rate)
- batch_size选择
- 其余超参数
- 误差
- 卷积神经网络典型CNN
-
- 简介
- LeNet-5
-
- 结构与重要讨论
- LeNet-5全流程详解
- LeNet论文
- AlexNet
-
- AlexNet结构
- 局部响应归一化(Local response normalization,LRN)
- AlexNet创新点
- AlexNet全流程详解
- 训练细节
- AlexNet论文
- LeNet与AlexNet结构对比
- ZF Net
-
- ZF Net结构
- 反向操作介绍
-
- 反池化(上采样)
- 反(转置)卷积
- 可视化
- 平移-缩放-旋转
- 卷积核选择
- ZF Net与AlexNet
- 验证模型可感知具体位置
- 不同部位的相关性
- ZFNet论文
- 对比AlexNet与ZFNet
- VGGNet(Visual Geometry Group Net)
-
- VGGNet结构
- 几个重要的问题
- 3x3卷积核的作用(优势)
- 1 x 1卷积核作用
- VGGNet论文
- ZFNet与VGGnet
- HOOK
- GoogLeNet
-
- 问题综述
- Inception module
- 模型
- 优点
- 训练细节
- GoogLeNet V2
- GoogleNet V3
- GoogleNet V4
- GoogLenet论文
- VGGNet与GoogLeNet
- ResNet
-
- 问题综述
- 残差结构介绍
- bottleneck的残差结构
- ResNet结构
- 再读Batch Normalization
- 迁移学习0
- ResNet论文
- DenseNet
-
- 问题综述
- DenseBlock+Transition
- DenseNet特点
- SeNet
-
- 问题综述
- Squeeze+Excitation
- SE-Inception+SE-ResNet
- ResNet论文
- MobileNet
-
- MobileNet介绍
- 深度可分离卷积
- 计算量对比
- 两个超参数
- MobileNetV2
- MobileNetV3
- ShuffleNet
-
- ShuffleNetV1
- ShuffleNetV2
- RepVGG
-
- 问题综述
- 选择VGG网络的原因
- RepVGG主体结构
- 多分支融合技术
-
- 卷积层和BN层合并
- 3x3卷积和1x1卷积融合
- identity分支等效特殊权重
- 融合最终结构
- 深层卷积
- MobileOne
-
- 问题综述
- 过参数化
- building block
- 训练优化技巧
- FasterNet
-
- 问题综述
- 部分卷积
- FasterNet网络
- 学习复现重点
- 区域卷积神经网络(Regions with CNN features,R-CNN)
-
- 目标检测简介
-
- 传统目标检测
- DPM
- 选择性搜索(Selective Search)
- 分层合并
- 交并比(Intersection over Union,IOU)
- mAP
- RCNN_NMS
- R-CNN
-
- 简介
- 回归微调(fine-tuning)
- 训练过程
- 训练建议
- 全流程
- SPP Net
-
- 简介
- 映射
- 空间金字塔
- SPPNet训练
- 训练建议
- 全流程
- Fast R-CNN
-
- 简介
- Fast R-CNN引入三种新技术
-
- RoI Pooling Layer
- 多任务损失函数(Multi-task loss)
- SVD
- 预训练
- 几个问题
- 全流程
- 训练建议
- 相对于SPPNet
- Faster R-CNN
-
- 简介
- RPN
- Anchor(锚点)
- ROL池化
- 正负样例
- 损失定义
- 全流程
- R-CNN、SPP Net、Fast R-CNN、Faster R-CNN
- R-FCN
-
- 全连接带来的问题
- ResNet中加入ROI层讨论
- 网络结构
- 全流程
- SSD
-
- 简介
- 亮点
-
- 重用Faster R-CNN的Anchors机制(Default boxes and aspect ratios)
- 多尺度特征图抽样(Multi-scale feature maps for detection)
- 全卷积网络结构(Convolutional predictors for detection)
- 结构
- 膨胀卷积
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
- 不同层次上的feature maps
- Achor
- 正负样例
- 数据增强和损失函数
- 预测
- 总结
全面-R-CNN、Fast/Faster/Mask R-CNN、FCN、RFCN 、SSD原理简析 - 知乎 (zhihu.com)
RCNN-FastRCNN-FasterRCNN-MaskRCNN_哔哩哔哩_bilibili
精彩-101-RCNN-FastRCNN-FasterRCNN理论合集_哔哩哔哩_bilibili
RCNN全系列详解及代码实现_哔哩哔哩_bilibili
像素级别的邻域特征
语义层面的抽象特征
候选框R
从变化的特征中提取不变的特征
目标检测简介
目标检测算法主要是基于深度学习模型,主要可以分为两大类:two-stage检测算法和one-stage检测算法
two-stage检测算法将检测问题划分为两个阶段,首先产生候选区域(region proposals), 然后对候选区域进行分类(一般需要进行位置精修),这类算法实现主要有:R-CNN、SPPNET、Fast R-CNN、Faster R-CNN等
one-stage检测算法是一种端到端的检测算法,直接进行区域定位与分类,这类算法实现主要有:SSD、YOLO、FPN等
目标检测:
- 图像分类(Image Classification)的目标是识别出图中出现的物体类别是什么,其功能主要是用于判断是什么?
- 图像定位(Object Location)的目标不仅仅需要识别出是什么物体(即分类),同时需要预测物体的位置信息,也就是单个目标在哪里?是什么?
- **目标检测(Object Detection)实质上上多目标的定位,即在一个图片中定位多个目标物体,包括分类和定位,**也就是多个目标分别在哪里?分别属于那个类别?
图像识别(Classification)
输入:图片
输出:物体的类别
评估方式:准确率图像定位(Localization)
输入:图片
输出:方框在图片中的位置(x,y,w,h)
评估方式:检测评价函数 Intersection-Over-Union(IOU)图像分类:VGG,GoogleNet,ResNet
图像定位:RCNN,Fast RCNN,Faster RCNN
目标检测:RCNN,Fast RNN,Faster RCNN,SSD,YOLO
检测图片中所有物体**(模型关注的物体)的类别标签(Category Label)和位置(最小外接矩形/Bounding Box)**
传统目标检测
传统的目标检测一般使用滑动窗口的框架,主要包括三个步骤:
- 利用不同尺寸的滑动窗口框出图中的某一部分作为候选区域
- 提取候选区域相关的视觉特征。比如人脸检测常用的Harr特征;行人检测常用HOG特征等
- 利用分类器进行识别,比如常用的SVM模型
DPM
可变形变部件模型 (Deformable Part Models, DPM) 是一种目标检测方法。DPM 被设计成能够有效地在图像中检测不同姿势和视角的对象,尤其是那些由多个部分组成的对象,如人和动物
DPM 的核心思想是表示一个目标对象不仅仅是一个单一的整体模板,而是由多个部件组成的,这些部件可以有一定的形变。通过这种表示,模型能够捕获对象的不同姿势和部件之间的相对位置变化
以下是 DPM 的主要概念和特点:
- 基于部件的表示:每个对象由一个主要部件(通常是中心)和多个辅助部件组成。例如,在人体模型中,主要部件可能是身体的中心,而辅助部件可以是头部、手臂和腿等
- 形变:辅助部件可以在一定范围内相对于主要部件进行形变。这种形变被约束在一个预定的范围内,从而允许模型在不同姿势和视角下检测对象
- 多尺度:DPM 被设计成可以在多个尺度上工作,这意味着它可以检测各种大小的对象
- 滑动窗口检测:DPM 使用滑动窗口方法遍历图像,评估每个窗口的位置和大小以确定是否存在目标对象
- 边缘直方图 (HOG) 特征:DPM 通常使用 HOG (Histogram of Oriented Gradients) 特征来描述图像中的部件。HOG 特征提供了图像局部的方向梯度信息,已被证明对于人和其他对象的检测非常有效
HOG:
HOG,即方向梯度直方图 (Histogram of Oriented Gradients),是主要用于对象检测的特征描述符。HOG的基本思想是:图像中对象的局部形状(或外观)可以通过局部强度梯度或边缘方向的分布来描述。HOG捕获图像的局部区域中的这种边缘或梯度结构,使其对局部几何和光度变换具有抵抗力
以下是HOG特征描述符的工作步骤:
- 灰度转换(可选):尽管不是强制性的,但通常将图像转换为灰度以简化信息并专注于结构方面
- 梯度计算:首先计算梯度值。通过使用简单的滤波器,图像进行卷积以计算x和y方向上的梯度。这些梯度有助于捕获轮廓和纹理信息
- 单元直方图:图像被划分为称为单元的小区域。对于每个单元,计算梯度方向(取向)的直方图。通常,直方图有9个区间,覆盖180度
- 块归一化:为了对光照变化和阴影产生的效应进行归一化,将相邻的单元组合成“块”,并对这些块进行归一化。这确保了HOG特征对局部光照和对比度变化具有稳健性
- 特征向量收集:最后,从所有块收集并连接HOG特征,形成最终的特征向量
HOG特征与支持向量机(SVM)分类器通常一起使用
选择性搜索(Selective Search)
一种目标用于目标检测的暴力方法就是从左往右,从上往下滑动窗口,利用分类识别目标,为了识别不同距离出检测不同的目标类型,可以使用不同大小、高宽比的窗口进行滑动,然后将窗口内的图片进行特征提取后送入分类器,进行分类判断即可完成目标检测的操作
很显然这种方法复杂度太高在穷举暴力法的基础上,进行一些剪枝操作,只选择固定大小和高宽比的窗口,这种方式在某些特定应用场景中是有效的,但是对于普通的目标检测而言,计算复杂度还是比较高的
为了解决刚刚的区域窗口获取过程中的问题,选择性搜索算法被提出来了,其问题的解决核心在于如何有效的去除冗余候选区域;在选择性搜索算法中,利用冗余候选区域大多是发生重叠的这个特征,自底向上的合并相邻的相似区域,从而减少冗余
选择性搜索过程:
该方法试图寻找图像中所有可能的有意义的对象。选择性搜索通过多尺度、多策略地合并超像素来生成目标提议以下是选择性搜索的基本步骤:
- 超像素分割:首先,使用一种方法(例如 SLIC、Quick Shift)将图像分割为超像素
- 分层合并:基于颜色、纹理、大小和形状相似性,逐步合并超像素,生成更大的区域。这会形成一个分层的结构
- 多尺度提议:从上述的分层结构中提取多种尺寸和形状的区域提议
- 提议后处理:可以进一步对提议进行过滤和调整,以生成一组最终的区域提议
分层合并
使用贪婪策略,计算两个相邻的区域的相似度,然后合并最相似的两块区域,直到最终只剩下一个完整的图像(S集合中没有相似度就结束区域的合并)
相似度量多样化
- 颜色相似度:
使用L1-norm归一化获取图像每个颜色通道的25bins直方图,这样每个区域可
以得到一个75维的向量,区域之间的相似度通过下列公式计算;值越大表示越
相似,值越小表示越不相似HOG——方向梯度直方图(Histogram of Oriented Gradient)
C i = { c i 1 , ⋯ , c i n } s c o l o u r ( r i , r j ) = ∑ k = 1 n min ( c i k , c j k ) . C t = s i z e ( r i ) × C i + s i z e ( r j ) × C j s i z e ( r i ) + s i z e ( r j ) . C_i=\{c_i^1,\cdots,c_i^n\}\quad s_{colour}(r_i,r_j)=\sum_{k=1}^n\min(c_i^k,c_j^k).\\\\C_t=\frac{\mathrm{size}(r_i)\times C_i+\mathrm{size}(r_j)\times C_j}{\mathrm{size}(r_i)+\mathrm{size}(\mathrm{r_j})}. Ci={ci1,⋯,cin}scolour(ri,rj)=k=1∑nmin(cik,cjk).Ct=size(ri)+size(rj)size(ri)×Ci+size(rj)×Cj.
- 纹理相似度
采用SIFT特征(尺度不变特征变换),具体特征求解做法为:对每个颜色通道的
8个不同方向计算方差σ=1的高斯微分;使用L1-norm归一化获取图像每个颜
色通道每个方向的10个bins的直方图,这样可以得到一个240维的向量(3810),其相似度计算方式以及合并后的纹理特征计算方式同颜色相似度计算过程
- 全局多尺度
如果仅仅基于颜色和纹理特征来进行合并的话,会导致合并之后的区域不断吞并周围的区域,后果就是多尺度仅应用与某个局部,而不是全局的多尺度,因此,需要给小的区域更多的权重,这样可以保证图像每个位置都是多尺度的合并,也就是优先合并小的区域
s s i z e ( r i , r j ) = 1 − I i z e ( r i ) + s i z e ( r j ) s i z e ( i m ) s_{size}(r_i,r_j)=1-\frac{\mathrm{Iize}(r_i)+\mathrm{size}(\mathrm{r_j})}{\mathrm{size}(im)} ssize(ri,rj)=1−size(im)Iize(ri)+size(rj)
距离
μ ^ l l ( r i , r j ) = 1 − size ( B B i j ) − size ( r i ) − size ( r i ) size ( i m ) \hat{\mu}ll(r_i,r_j)=1-\frac{\operatorname{size}(\boldsymbol{B}B_{ij})-\operatorname{size}(r_i)-\operatorname{size}(r_i)}{\operatorname{size}(im)} μ^ll(ri,rj)=1−size(im)size(BBij)−size(ri)−size(ri)<