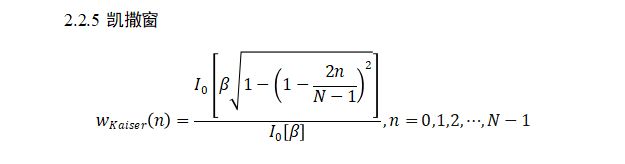间接法加窗分析信号的功率谱

     

       本篇文章是博主在通信等领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对通信等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在   通信领域笔记：

          通信领域笔记（3）---《间接法加窗分析信号的功率谱》

间接法加窗分析信号的功率谱

目录

1、设计要求

2、理论分析推导

 2.1间接法理论分析

 2.2窗函数理论分析

3、仿真及结果分析

3.1.1五种窗函数的时域频域比较

3.1.2五种窗函数进行截断的频谱泄露差异

3.1.3 五种窗函数计算功率谱

---

1、设计要求

---

2、理论分析推导

2.1间接法理论分析

        维纳辛钦定理指出，随机信号的相关函数与它的功率谱是一对傅里叶变换对。BT法就是基于这个原理。先由观测数据估计出自相关函数，然后求自相关函数的傅立叶变换，以此变换作为对功率谱的估计，也称为间接法。BT法要求信号长度N以外的信号为零，这也造成BT法的局限性。

  2.2窗函数理论分析

        当输入一个信号，我们需要截取它其中的一段来进行研究，就可以用加窗来实现，这里窗长就是截取长度。但因为之后我们会研究截取信号的频谱，需要对其进行傅里叶变换，而傅里叶变换又是作用于正负无穷的，所以要先对截取信号进行周期扩展。

        此时，若截取为整周期截取，周期扩展之后还是原信号，因此不会出现频谱泄露；若为非整周期截取，或信号根本就不是周期信号，截取信号不能表示整个信号，周期扩展之后信号的频谱会在每个周期相连的地方出现高次谐波，产生Gibbs现象，造成频谱泄露。

        这里可以延伸出一个如何选择窗函数来减小频谱泄露的问题。即要求窗函数频谱的主瓣尽量窄、旁瓣衰减尽量大。但二者不可兼得，因此要根据实际需求选择窗函数。主瓣越窄的窗函数的频率识别精度越高；旁瓣衰减越大的窗函数的幅度识别精度越高。

        每次FFT变换只能对有限长度的时域数据进行变换，因此，需要对时域信号进行信号截断。即使是周期信号，如果截断的时间长度不是周期的整数倍（周期截断），那么，截取后的信号将会存在泄漏。为了将这个泄漏误差减少到最小程度，我们需要使用加权函数，也叫窗函数。

        加窗主要是为了使时域信号似乎更好地满足FFT处理的周期性要求，减少泄漏。而窗函数的实质是，时域上与输入信号相乘，频域上，与输入信号做卷积。针对于常用的五种窗函数：矩形窗、汉明窗、汉宁窗、布莱克曼窗、凯撒窗进行分析和仿真。

         这种窗函数在时域上近似于一个扁长的椭圆，它在频域上使主瓣能量与旁瓣能量之比达到最大。与其他窗函数相比，凯撒窗的一个显著特点是它可以同时调整主瓣和旁瓣的宽度。例如，当β增加时，相对旁瓣衰减降低，而主瓣宽度则会增加。

---

3、仿真及结果分析

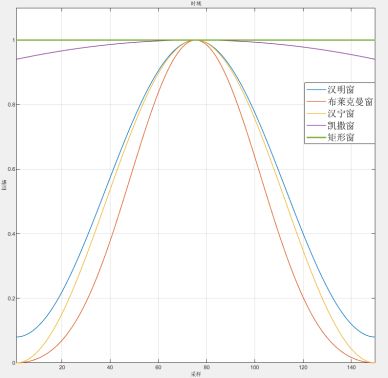
3.1.1五种窗函数的时域频域比较

比较五种窗函数的旁瓣高度以及主瓣宽度。

 从频域图可以看出，旁瓣衰减程度从大到小排列依次为：

        布莱克曼窗 > 汉宁窗 > 汉明窗 > 矩形窗 > 凯撒窗

主瓣宽度从大到小排列依次为：

        矩形窗 > 凯撒窗 > 汉明窗 > 汉宁窗  > 布莱克曼窗

        主瓣宽度的增加会导致频谱的分辨率降低。因此，对于窗函数而言，频谱分辨率和旁瓣的衰减不可兼得。

3.1.2五种窗函数进行截断的频谱泄露差异

 

 3.1.3 五种窗函数计算功率谱

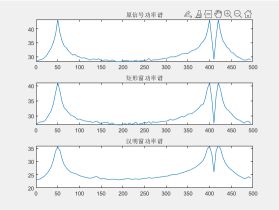
间接法加窗求解的窗函数功率谱图比较

       

 加入5dB、0dB、-5dB、-10dB高斯白噪声功率谱比较图：

                          

                          

---

补充信号功率谱分析

Welch法加窗求解的窗函数功率谱图比较

                           

 

 4、Matlab程序实现

%% 时间：2023.11.8

%通过Matlab产生如下信号：x(n)=2cos(2pif1n)+2cos(2pif2n)+2cos(2pif3n)+v(n)
%其中f1=0.05、f2=0.40、f3=0.42，
% v(n)是实高斯白噪声（信噪比由5dB至-10dB，步进5dB），f1-f3均为归一化的频率。
%针对间接法，首先产生不同的窗函数;
%观察不同窗函数（矩形、布莱克曼、汉宁、汉明、凯撒等）的时域、频域情况，
%总结不同窗函数的优缺点;
%然后使用不同的窗函数进行处理观察功率谱变化情况，并分析产生结果的原因。

clc;
clear;
close all;

%% 信号的生成
N=200;%采样点数
Fs = 1000;  %采样频率
fc1 = 0.05*Fs; % 归一化载波频率转化为载波频率
fc2 = 0.40*Fs;
fc3 = 0.42*Fs;
n = 0:1/Fs:(N-1)/Fs;

xn = 2*cos(2*pi*fc1*n) + 2*cos(2*pi*fc2*n) + 2*cos(2*pi*fc3*n);
xn = awgn(xn,5);  %加入高斯白噪声信号
nfft = N;

%% 窗函数的时域频域分析
window1=zeros(1,N);
window2=zeros(1,N);
window3=zeros(1,N);
window4=zeros(1,N);
window5=zeros(1,N);
L = 3*N/4;
a1=transpose(hamming(L)); %汉明窗
a2=transpose(blackman(L)); %布莱克曼窗
a3=transpose(hann(L)); %汉宁窗
a4=transpose(kaiser(L)); %凯撒窗
a5=transpose(boxcar(L)); %矩形窗
for i=1:L
    window1(i)=window1(i)+transpose(a1(i));
    window2(i)=window2(i)+transpose(a2(i));
    window3(i)=window3(i)+transpose(a3(i));
    window4(i)=window4(i)+transpose(a4(i));
    window5(i)=window5(i)+transpose(a5(i));
end

%% 五种窗函数的时域频域比较
 wvt = wvtool(a1,a2,a3,a4,a5);
 legend(wvt.CurrentAxes,'汉明窗','布莱克曼窗','汉宁窗','凯撒窗','矩形窗');

%% 窗函数采样点全选取
% L = N;
% window1=transpose(hamming(L)); %汉明窗
% window2=transpose(blackman(L)); %布莱克曼窗
% window3=transpose(hann(L)); %汉宁窗
% window4=transpose(kaiser(L)); %凯撒窗
% window5=transpose(boxcar(L)); %矩形窗

%% 单个窗函数的时域频域分析
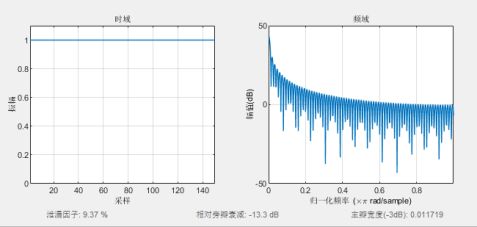
wvtool(boxcar(L));
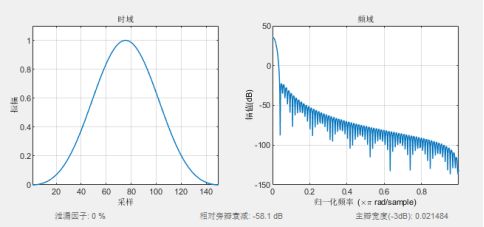
wvtool(hamming(L));
wvtool(blackman(L));
wvtool(hann(L));
wvtool(kaiser(L));

%% 间接求功率谱法
%间接法先由序列x(n)估计出自相关函数R(n),
%然后对R(n)进行傅里叶变换，便得到x(n)的功率谱估计

%加窗后的信号
xn1=xn.*window1;
xn2=xn.*window2;
xn3=xn.*window3;
xn4=xn.*window4;
xn5=xn.*window5;

%计算序列的自相关函数
%不加窗自相关函数的傅里叶变换
cxn = xcorr(xn);
CXk = fft(cxn,nfft);
Pxx = abs(CXk);
%汉明窗自相关函数的傅里叶变换
cxn1 = xcorr(xn1);
CXk1 = fft(cxn1,nfft);
Pxx1 = abs(CXk1);
%布莱克曼窗自相关函数的傅里叶变换
cxn2 = xcorr(xn2);
CXk2 = fft(cxn2,nfft);
Pxx2 = abs(CXk2);  
%汉宁窗自相关函数的傅里叶变换
cxn3 = xcorr(xn3);
CXk3 = fft(cxn3,nfft);
Pxx3 = abs(CXk3);  
%凯撒窗自相关函数的傅里叶变换
cxn4 = xcorr(xn4);
CXk4 = fft(cxn4,nfft);
Pxx4 = abs(CXk4);  
%矩形窗自相关函数的傅里叶变换
cxn5 = xcorr(xn5);
CXk5 = fft(cxn5,nfft);
Pxx5 = abs(CXk5);  

index = 0:round(nfft/2-1);
f = index*Fs/N;
plot_Pxx = 10*log10(Pxx(index+1)); 
plot_Pxx1 = 10*log10(Pxx1(index+1)); 
plot_Pxx2 = 10*log10(Pxx2(index+1)); 
plot_Pxx3 = 10*log10(Pxx3(index+1)); 
plot_Pxx4 = 10*log10(Pxx4(index+1)); 
plot_Pxx5 = 10*log10(Pxx5(index+1)); 

%% 窗函数功率谱图比较
figure(7);
subplot(311);
plot(f,plot_Pxx);
title('原信号功率谱');
subplot(312);
plot(f,plot_Pxx5);
title('矩形窗功率谱');
subplot(313);
plot(f,plot_Pxx1);
title('汉明窗功率谱');

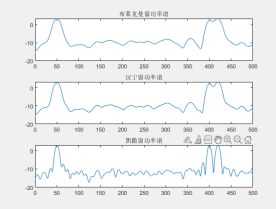
figure(8);
subplot(311);
plot(f,plot_Pxx2);
title('布莱克曼窗功率谱');
subplot(312);
plot(f,plot_Pxx3);
title('汉宁窗功率谱');
subplot(313);
plot(f,plot_Pxx4);
title('凯撒窗功率谱');

figure(9);
hold on
plot(f,plot_Pxx);
plot(f,plot_Pxx1);
plot(f,plot_Pxx2);
plot(f,plot_Pxx3);
plot(f,plot_Pxx4);
plot(f,plot_Pxx5);
title('五种窗功率谱比较');
legend('原信号','汉明窗','布莱克曼窗','汉宁窗','凯撒窗','矩形窗');
hold off

---

     文章若有不当和不正确之处，还望理解与指出。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请联系博主删除。如有错误、疑问和侵权，欢迎评论留言联系作者，或者关注VX公众号：Rain21321，联系作者。