超详细讲解前缀和、二维前缀和、差分、二维差分

自我介绍：hello!这里是欧_aita的频道，一个初学数据结构与算法的小白。
今日语录: 成功不是最终的，失败也不是致命的。重要的是勇气，要有继续前进的勇气。
祝福语：愿你的代码生活充满注释，逻辑清晰，debug之路畅通无阻。
大家可以在评论区畅所欲言，可以指出我的错误，在交流中共同进步。
如果你也恰好在学习C++或者数据结构与算法那就来看看主页吧!– 欧_aita

一. 前缀和※

1.1 一维前缀和⭐

1.1.1 前缀和的定义

前缀和（Prefix Sum）是一种数组预处理技术，用于高效地计算数组中某个范围内元素的和。前缀和数组是原始数组的元素依次累加的结果。

1.1.2 朴素方法

这里的朴素算法时间复杂度为O(n*m)

const int N = 1e5 + 10;
int a[N];
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
while(m--)
{
    int l, r;
    int sum = 0;
    scanf("%d%d", &l, &r);
    for(int i = l; i <= r; i++)
    { 
        sum += a[i];
    }
    printf("%d\n",sum);
}

1.1.3 前缀和的时间复杂度

计算前缀和的时间复杂度是线性的，即 O(n)，其中 n 是数组的长度。这是因为计算前缀和涉及对数组进行一次顺序遍历，并且每个元素只被访问一次。

具体来说，计算前缀和的步骤包括：
初始化一个前缀和数组，长度为原始数组长度加一。
从数组的第一个元素开始，依次累加得到前缀和数组的每个元素。
最终得到前缀和数组，其中每个元素表示原数组中对应位置之前所有元素的和。
由于每个元素只被访问一次，所以总体的时间复杂度是 O(n)。
这使得前缀和成为一种高效的预处理技术，特别是在需要多次查询数组中某个范围的元素和时。

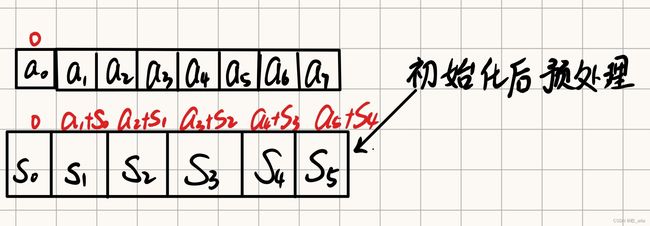
1.2 一维前缀和的理论⭐

先初始化预处理
预处理后的前缀和数组
可以看出求a2与a4之间的和就是S4-S1

1.3 一维前缀和的代码讲解⭐

1.3.1 求出前缀和数组

默认a0=0,数组下标从1开始使用

for(int i=1;i<=n;i++)
{
    s[i]=s[i-1]+a[i];//s[0]默认为0
}

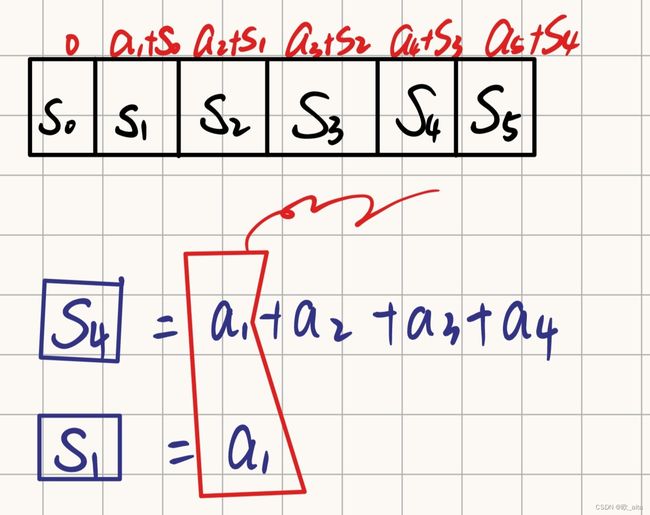
1.3.2 求出两个数组元素之间的和

先给数组元素l与r赋值，这是我们要求出的区间之和sum=a[l]+…+a[r]

sum=s[r]-s[l-1];

1.3.3 整体

注意使用scanf/printf与cin/cout该如何选择
若n大于一百万，就是用scanf/printf。否则使用cin/cout，这可以提高代码运行效率

#include 
using namespace std;
//前缀和O（n）

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);

	for (int i = 1; i <= n; i++)s[i] = s[i - 1] + a[i];
	while (m--)//m表示操作次数
	{
		int l, r;
		scanf("%d%d", &l, &r);
		printf("%d\n", s[r] - s[l - 1]);
	}
	system("pause");
	return 0;
}

二. 二维前缀和※

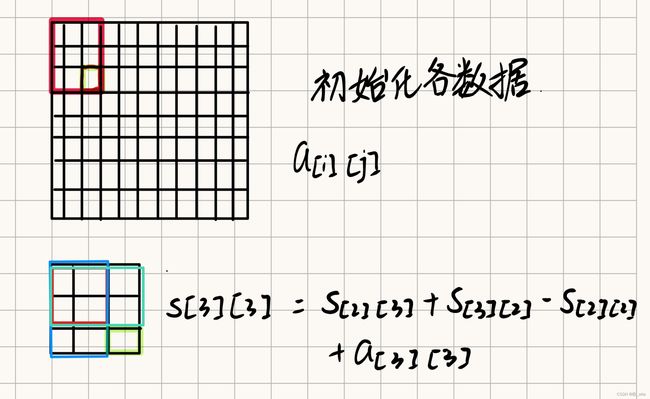
2.1二维前缀和的理论⭐

初始化数据

慢慢理解,这是求一个范围内的前缀和

2.2 二维前缀和的代码讲解⭐

2.2.1 初始化（两步）

n表示行数，m表示列数，q表示操作次数与下文对应

scanf("%d%d%d",&n,&m.&q)
for(int i=1;i<=n;i++)
{
    for(int j=1;j<=n;j++)
    {
        scanf("%d",&a[i][j]);
    }
}

for(int i=1;i<=n;i++)
{
    for(int j=1;j<=n;j++)
    {
        s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
    }
}

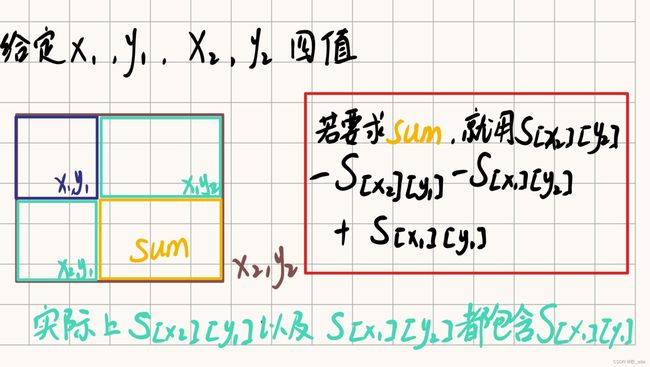
2.2.2 查询子矩阵内的前缀和

while(q--)
{
    int x1,x2,y1,y2;
    scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
    //求子矩阵
    printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}

2.2.3 整体

#define _CRT_SECURE_NO_WARNINGS
#include 
using namespace std;

const int N = 1010;
//二维矩阵左上角所有元素和
int n, m, q;
int a[N][N], s[N][N];



int main()
{
	scanf("%d%d%d", &n, &m, &q);
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &a[i][j]);
		}
	}

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			//求前缀和
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
		}
	}
	while (q--)
	{
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		//算子矩阵的和
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}
	system("pause");
	return 0;
}

三. 差分※

3.1 一维差分⭐

3.1.1 一维差分的定义

举个例子，s[]数组是表示b[]数组前缀和的数组，此时b[]数组就是s[]数组的差分数组。
而b[i]=s[i]-s[i-1]。

3.1.2 一维差分的时间复杂度

对于差分数组的构建，时间复杂度是 O(n)，其中 n 是数组的长度。这是因为对原始数组的每个元素都需要计算差分数组中的一个元素，总共需要进行 n 次操作。
在使用差分数组进行范围更新时，时间复杂度也是 O(1)，因为只需要更新差分数组中两个位置的值。
总的来说，差分的时间复杂度主要取决于构建差分数组的过程，而构建差分数组的时间复杂度是 O(n)。

3.1一维差分的应用⭐

如果我们要让一段s[]前缀和数组加上int c，如果要使用for()循环遍历，这个过程的时间复杂度是O(n)，而使用差分数组b[l]+=c,而c[r]-=c，很显然这个过程的时间复杂度是O(1)。

3.2 一维差分的代码讲解⭐

3.2.1 插入c

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

这个过程就是O(1)。

3.2.2 求前缀

s[]数组是抽象出来的一个数组，实际在插入后的过程用for循环可求出

for(int i=1;i<=n;i++) b[i]+=b[i-1];

3.2.3 整体

#define _CRT_SECURE_NO_WARNINGS
#include 
using namespace std;

const int N = 10010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

int main()
{
	scanf("%d", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);

	for (int i = 1; i <= n; i++)insert(i, i, a[i]);

	while (m--)
	{
		int l, r, c;
		scanf("%d%d%d", &l, &r, &c);
		insert(l, r, c);
	}

	for (int i = 1; i <= n; i++)b[i] += b[i - 1];

	for (int i = 1; i <= n; i++)printf("%d", b[i]);

	return 0;
}

四.二维差分※

4.1 二维差分的代码实现⭐

理论部分结合二维前缀和和一维差分结合即可

#define _CRT_SECURE_NO_WARNINGS
#include 
using namespace std;

const int N = 10010;

int n, m,q;
int a[N][N], b[N][N];

void insert(int x1, int x2, int y1,int y2,int c)
{
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}

int main()
{
	scanf("%d%d%d", &n, &m,&q);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			scanf("%d", &a[i][j]);

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			insert(i, j, i, j, a[i][j]);

	while (q--)
	{
		int x1, y1, x2, y2, c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1, y1, x2, y2, c);
	}

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)printf("%d", b[i][j]);
		puts("");
	}
	return 0;
}

这篇文章就到此为止，如果觉得读完后对你有所帮助的话就点个赞吧，你们的支持是我最大的动力！