机试(蓝桥杯)入门级教程
文章目录
- 一、都要干什么呢
- 二、题目及分类
- 1. 堆栈
-
- 1.1 堆栈的翻转
- 1.2 不同括号的匹配
-
-
- 题目描述*
- 注意:
-
- 1.3 带优先级的不同括号的匹配
-
-
- 思路:
-
- 1.4 带特殊要求的例题
-
- 思路:
- 难点:
- 2.优先队列通用模板!
-
- 2.1功能函数:
- 2.2 合并果子
- 2.枚举
-
-
-
- 2.1 **题目描述**
-
- 枚举-双层循环
-
-
- 2. 2 题目描述
- 2.3 题目描述(蓝桥杯)
- 2.4人物相关性
- 思路:用滑动区间(两个指针)的思想,当Bob处于Alice的区间内时,记录有多少个Bob处于Alice的区间内。
-
-
- 3.排序
-
-
-
- 3.1 冒泡排序
- 3.2. 选择排序
- 3.3.直接插入排序(设置哨兵)
- 3.4.二分法排序
- 3.5.快速排序(背过!)
- 堆排序
-
-
- 5.贪心算法
-
-
- 贪心99%情况下要用到排序
- 5.1 题目描述*
- 5.2 题目描述**
- 5.3 最大路径
- 思路:
-
- 6.两数相除--递归解法
- 7.二叉树
-
-
- 7.1 二叉树的翻转--递归解法
- 7.2 相同的二叉树---同时遍历两棵树
- 7.3 树路径总和---递归--背过!
- 7.4 二叉排序树
- 7.4 将有序数组(从小到大排列)转为二叉搜索树----递归----背过!
- 7.5 二叉树的最大深度
- 7.6 二叉树的层序遍历(其实就是图论中的广度优先搜索,并且是简化版)
- 7.7 二叉树的前序遍历
- 7.8 表演一个高度平衡的二叉搜索树的创建 及 层序遍历
- 7.9 二叉树各种基本操作总结
- 7.10 哈夫曼编码
-
- 8.字符串
-
- 8.1 切割字符串
- 8.2 翻转字符串里的单词
- 9. 链表类问题
-
- 9.1 约瑟夫环
- 注意:
- 9.2 单链表实现两个数的加法
-
-
- 注意:
-
- 10.进制转换类问题
-
- 10.1 反序数
- 10.2 10进制转 小于等于9 进制
- 10.3 10进制转 10以上 进制(通用模板)
-
-
- 注意:
-
- 10.4 小于等于9 进制转10进制
-
-
- 注意:
-
- 10.5 10以上进制转10进制
-
-
- 注意:
-
- 10.6 X进制转Y进制--以十进制当做桥梁(即x->10->y)
-
- 10.6.1 如果2<=X,Y<=9
- 10.6.1 如果10
- 注意:
- 10.7 进阶例题
- 代码的难点在于
- 11. 排版类问题
-
- 11.1 三角形
- 11.2 字符菱形
- 11.3 矩阵旋转--找规律!
-
- 11.3.1 顺时针翻转90°
- 11.3.2 顺时针翻转180°
- 11.3.3 逆时针翻转90°
- 11.4 矩阵翻转
- 11.5 杨辉三角
- 12. 日期类
-
- 12.1 闰年
- 12.2 本年的第几天
- 注意:
- 13、常见数学公式
-
- 13.1 错位问题
- 13.2 海伦公式
- 14.大数问题(高精度)
-
- 14.1 大数加法
-
-
- 思路:
- 代码注意:
-
- 14.1 大数减法
-
-
- 注意:
-
- 14.3 大数乘法
一、都要干什么呢
1.常用排序算法
2.只需要学递归、分治、贪心、动态规划
3.可以学一下STL库函数
4.编程题可以只写输入输出语句,与样例即可(因为第一个测试数据一般就是样例)

5.判断是否超时(是否需要优化)小技巧
蓝桥杯的编译器的运算水平可以达到10^8,如果给你的数据范围在number <= 10^5 ,时 ,如果你用了双层循环,时间复杂度是O(n^2),那么你就会超时(10 ^10 > 10^8)。
二、题目及分类
1. 堆栈
C++提供了堆栈类stack,其函数有:
empty():判断堆栈是否为空,为空返回true
pop(): 弹出栈顶元素,无返回值
push(i):将元素i压入栈顶,无返回值
size():返回堆栈元素个数
top():返回栈顶元素
需要的头文件、堆栈的定义、简单使用
#include1.1 堆栈的翻转
翻转堆栈,借助另一个堆栈,主要看下面的st1=st2
# include 1.2 不同括号的匹配
题目描述*
注意:
(0)如果是合法的,那么压入右括号时肯定紧挨着左括号,比如输入{[()]},压入}时,堆栈里的下面一个应该是{
(1)for(char c:s)遍历string
(2)如果堆栈是空,st.top()是非法的,在else if中如果没有st.empty的判断,会出现内存错误,所以使用top函数的时候最好(大部分情况下)判断一下堆栈是否为空。你以为注意这些就够了吗?还要注意if(!st.empty()&&(map[st.top()]+3==map[c])),是否为空的判断要在top的使用之前!!
哈希表解法
class Solution {
public:
bool isValid(string s) {
unordered_map<char,int> map{ {'(',1}, {'[',2}, {'{',3}, {')',4}, {']',5}, {'}',6}}; //哈希表
stack<char> st;
bool flag=true;
for(char c:s){ //可以这样遍历string的每一个char
if(map[c]>=1&&map[c]<=3) //哈希表的索引用[]
st.push(c);
else if(!st.empty()&&(map[st.top()]+3==map[c])) //如果没有empty的话,会报内存错误
st.pop();
else
return false;
}
if(!st.empty())
return false;
else
return true;
}
};
优解二,这个解法非常好理解,并且只用到了栈。
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for(char c:s){
if(c=='('||c=='{'||c=='['){
st.push(c);
}else if(c==')'&&!st.empty()&&st.top()=='('){ //!!写成st.top()=='('&&!st.empty(),就会报错因为与条件之间也有先后的执行关系
st.pop();
}else if(c=='}'&&!st.empty()&&st.top()=='{'){
st.pop();
}else if(c==']'&&!st.empty()&&st.top()=='['){
st.pop();
}else{
return false;
}
}
if(st.empty())
return true;
else
return false;
}
};
1.3 带优先级的不同括号的匹配

上一题的代码只需要看右半部分的括号是否和栈顶匹配,而只要是括号的左半部分,不经过处理直接入栈。
这道题就要从左半部分入手了。
思路:
(1)比较括号的优先级,只看括号的左半部分或者右半部分就可以,那我们选择左半部分,因为右半部分不在栈里面呀。
(2)如果此时栈里是这样的
| bottom | { | [ | < | top+1 |
|---|---|---|---|---|
| 我此时再入栈一个“(”,还需要把前面的所有括号都比较一遍优先级吗?不需要。只要跟栈顶那个“<”比较就行了。 |
# include1.4 带特殊要求的例题
给定字符串,可能包含的字符有’(', ‘)’, 字母三种情况。注意,只有一种类型的括号。遇到不能匹配的左括号,输出‘$’;找到不能匹配的右括号,输出‘?’。其他情况(能匹配的左括号、右括号、字母)f都输出空格

这是北大的一道机试题,看了解析是将字符串遍历两遍,我没看懂。但是我的思路简直妙啊。妙就妙在定义了三个堆栈。
思路:
只需要遍历一遍字符串,记录不能匹配的左括号和右括号的下标。最后利用下标重新给字符串赋值$或者?就可以了。
怎样记录下标呢?用两个堆栈分别记录,暂且称为left和right吧。
(1)当字符是“(”,left入栈(记录没有匹配的左括号),st也入栈。
(2)当字符是")"时,如果st为空,那么right入栈(记录没有匹配的右括号),st也入栈;如果st不空,并且栈顶是“(”时,匹配成功,st弹出栈顶,left也弹出栈顶(删除一个左括号的记录);如果st不空,但栈顶不是“(”时,right入栈(记录没有匹配的右括号),st也入栈。
(3)遍历完字符串后,left和right里分别存放着没有匹配成功的左括号和右括号的下标
难点:
难点在于for循环内几种可能情况的考虑。建议,首先考虑字母;然后考虑左括号(堆栈为空怎样?不空怎样?),再考虑右括号(堆栈为空怎样?不空怎样?)
#include2.优先队列通用模板!
优先队列:入队列以后按照规定的方式(降序或升序)排序,不再是先进先出了。
2.1功能函数:
priority_queue<int> q; //定义
q.push(123); //入队列
int temp=q.top(); //查看队首元素
q.pop();//队首出队列
int size=q.size();//大小
q.empty();
需要注意的是,普通队列查看队首元素用的是q.front()函数;而优先队列用的是和堆栈一样的q.top()函数
2.2 合并果子
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过 n−1 次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为 1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3 种果子,数目依次为 1,2,9。
可以先将 1、2 堆合并,新堆数目为 3,耗费体力为 3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。
解法一:哈弗曼树,其实一眼就能看出这是个哈弗曼树
解法二:优先队列
要背过大顶堆那里的代码!
#include其实这个题可以不用结构体node作为队列的元素,直接用整形数值int就行。但是上面那种是通用模板!!要记还是得记上面那种!!
#include2.枚举
2.1 题目描述
(1).假设你有一个数组,其中第\ i i 个元素是股票在第\ i i 天的价格。
你有一次买入和卖出的机会。(只有买入了股票以后才能卖出)。请你设计一个算法来计算可以获得的最大收益。
枚举-双层循环
class Solution {
public:
/**
*
* @param prices int整型vector
* @return int整型
*
* 编程思路是双层循环
* 最外层得到总的最大利润,用profit记录
* 内层得到对于每一天买入的最大利润,用temp记录
*/
int maxProfit(vector <int>&prices) {
// write code here
int i;
int j;
int temp; //对于每个prices[i]的最大收益
int profit=0; //最大收益
for (i=0;i<prices.size()-1;i++) //!!!!!!!
{
temp=0;
for(j=i+1;j<=prices.size()-1;j++)
{
if((prices[j]-prices[i])>temp)
temp=prices[j]-prices[i];
}
if(temp>profit)
profit=temp;
}
return profit;
}
};
出错之处:
测试用例为[1,4,9]时,结果应该是“8”,却得到了“35678”这样大的数,我就考虑是数组越界了。
果然是在对i和j的使用上出了问题,i和j代表数组的下标,
而数组下标的最大值应该是prices.size()-1而不是prices.size()
2. 2 题目描述
(1)在最后一个for循环中,遍历所有字符,列举了所有可能性
(2)对于每一个字符,都是从后往前看,即看见了X不去想它的后面会不会是“L”(因为你要是这一遍把下一遍的顺便处理了,拿下一个for循环就不知道干啥了),只去看前面是不是“I”。既然要看前一个字符,那么就需要把所有的字符放入一个数组里。
class Solution {
public:
int romanToInt(string s) {
int sum=0;
char a[16];
int size=s.length(); //length函数获取字符串长度
int i=0; //这样把字符串放入字符数组里
for(char c:s){
a[i]=c;
i++;
}
for(int i=0;i<size;i++){
if(a[i]=='I')
sum=sum+1;
else if(a[i]=='V'){
if((i-1)>=0&&a[i-1]=='I'){ //判断V的前面i-1是否还有,这样避免V是a[0],a[i-1]造成内存泄漏!
//并且对i-1的判断放在前面哦!!
sum=sum-1+4;
}else sum=sum+5;
}else if(a[i]=='X'){
if((i-1)>=0&&a[i-1]=='I'){
sum=sum-1+9;
}else sum=sum+10;
}else if(a[i]=='L'){
if((i-1)>=0&&a[i-1]=='X'){
sum=sum-10+40;
}else sum=sum+50;
}else if(a[i]=='C'){
if((i-1)>=0&&a[i-1]=='X'){
sum=sum-10+90;
}else sum=sum+100;
}else if(a[i]=='D'){
if((i-1)>=0&&a[i-1]=='C'){
sum=sum-100+400;
}else sum=sum+500;
}else if(a[i]=='M'){
if((i-1)>=0&&a[i-1]=='C'){
sum=sum-100+900;
}else sum=sum+1000;
}
}
return sum;
}
};
2.3 题目描述(蓝桥杯)
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:
1. 形状是正方形,边长是整数
2. 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?
输入格式
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
样例输入
2 10
6 5
5 6
样例输出
2
解析:一开始想的是从所有巧克力的最小边长枚举到1,只有一个测试用例通过了。原因是如果有两块巧克力:1×7和5×6,有一个小朋友,那么他应该吃5×5的巧克力。如果从所有巧克力的最小边长枚举到1,他只能吃到1×1的巧克力。这就提醒了我,应该从最大边长开始枚举,枚举到1.
# include2.4人物相关性
直观的思路是用数组(向量)记录Alice和Bob的位置,然后用两重for循环判断if(|alice-bob|<=20) count++。
上述思路的时间复杂度是O(n^2),这里给出进阶版的代码,省去一重循环,使时间复杂度缩小。
思路:用滑动区间(两个指针)的思想,当Bob处于Alice的区间内时,记录有多少个Bob处于Alice的区间内。
打代码的过程中需要注意的是:
(1)string input的输入如果带有空格,必须用getline(cin,input)的形式,否则空格后的无效。
(2)能用数组就不用向量。向量的size函数push_back函数不香吗?
(3)Bob的滑动区间只能是左闭右开。用纸模拟一下就知道了。
(4)注意判断区间右指针是否大于左指针,我没模拟出左大于右的这种情况,但还是加上这个if(rp>lp)吧小心为妙。
# include3.排序
3.1 冒泡排序
#include 3.2. 选择排序
注意:每一趟记录的是下标min
class Solution {
public:
bool canMakeArithmeticProgression(vector<int>& arr) {
int min;
for(int i=0;i<=arr.size()-2;i++){
min=i;
for(int j=i+1;j<=arr.size()-1;j++){
if(arr[j]<arr[min])
min=j;
}
swap(arr[i],arr[min]); //调用的系统函数
}
int diff=arr[1]-arr[0];
for(int i=1;i<=arr.size()-2;i++){
if((arr[i+1]-arr[i])!=diff)
return false;
}
return true;
}
};
3.3.直接插入排序(设置哨兵)
注意:
(1)传整个数组的话,传的是首地址。接收函数的参数是int *a(地址的形式)
# include3.4.二分法排序
其实就是将二分查找技术融入了插入法。如下图,直接插入法是将“4”依次和前面的“6”、“5”、“2”比较。而二分法是二分着比较。
既然用到了插入法,必须要有哨兵。上一次的代码用a[0]作为哨兵,所以a[0]没有参与排序。这次直接用变量temp做哨兵,让a[0]也跟着排序。
# include3.5.快速排序(背过!)
(1)快速排序的本质就是把基准数大的都放在基准数的右边,把比基准数小的放在基准数的左边。
并且,这应该是是一个递归的过程,递归出口在于low=high时。
(2)指针low和high一个指向没有被比较过的,另一个指向无效的位置(该位置的元素被移走了),也就是下一个要被比较的。以high为例,在 getMid函数内先进行while(a[high]>=temp),然后再high–,也就是while-do,而不是do-while。
(3)一定要先从右边的指针开始移动,因为把左边的第一个当做比较的基准了,所以左指针指的那个位置是无效的,需要先用右边第一个比基准小的填死那个无效的位置
# include
while(low<high&&a[low]<=temp){
low++;
}
a[high]=a[low];
}
//low=high时,a[low]=a[high]=和周围重复,可以用来放基准temp
a[low]=temp;
return low;
}
void quickSort(int *a,int low,int high){
if(low<high){
int mid=getMid(a,low,high);
quickSort(a,low,mid-1);
quickSort(a,mid+1,high);
}
}
int main(){
int a[10]={12,1,4,7,3,2,5,6,9,8};
quickSort(a,0,9); //传整个数组的话,传的是首地址。接收函数的参数是int *a(地址的形式)
for(int i=0;i<=9;i++){
printf("%d,",a[i]);
}
return 0;
}
如果要降序,只需要把getMid里的》=和《=号互换一下
while(low<high&&a[high]<=temp){//!!!!!
high--;
}
a[low]=a[high];
while(low<high&&a[low]>=temp){//!!!!!
low++;
}
a[high]=a[low];
}
堆排序
#include5.贪心算法
贪心99%情况下要用到排序
5.1 题目描述*

(1)为什么说是贪心算法:
账单是20的情况,为什么要优先消耗一个10和一个5呢?
因为美元10只能给账单20找零,而美元5可以给账单10和账单20找零,美元5更万能!
所以局部最优:遇到账单20,优先消耗美元10,完成本次找零。
全局最优:完成全部账单的找零。
(2)注意:这个题的关键思路在于,需要记录的不是已拥有的金钱总数,而是5元、10元、20元纸币的个数。
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int money[3]={0,0,0}; //数组的妙用!!!!!!!!!!
int size=bills.size();
for(int i=0;i<size;i++){//遍历顾客
if(bills[i]==5){
money[0]++; //收入5元
}else if(bills[i]==10){
if(money[0]>=1){
money[0]--; //给出5元
money[1]++; //收入10元
}else
return false;//找不开10元了
}else{
if(money[0]>=1&&money[1]>=1){
money[0]--;//给出5元
money[1]--;//给出10元
money[2]++;//收入20元
}else if(money[0]>=3){
money[0]=money[0]-3;//给出15元
money[2]++;//收入20元
}else
return false;
}
}
return true;//如果能顺利遍历完,那么就没错
}
};
5.2 题目描述**

(1)为什么是贪心算法?
每遍历一个数,都去考虑当前所能到达的最远下标。
class Solution {
public:
bool canJump(vector<int>& nums) {
int far=0;//最大的应该是被不断更新的
for(int i=0;i<nums.size();i++){
if(i>far) //当前所能到达的最远距离到不了i了
return false;
else
far=max(far,i+nums[i]);
}
return true;
}
};
(2)用动态规划求解更好理解
①定义子问题:f(i):当前位置为i时,能到达的最远距离,用DP数组记录。
②子问题的递推关系:
dp[i]=max(dp[i-1],i+nums[i])
③边界:dp[0]=nums[0]
注意:要注意的是会出现到不了下一步的情况,也就是说不是所有的dp[i]都能计算出来的(这一点和以往的动态规划不同)。
class Solution {
public:
bool canJump(vector<int>& nums) {
int size=nums.size();
int dp[size];
dp[0]=nums[0];// 边界
for(int i=1;i<size;i++){
if(dp[i-1]<i) //如果到不了下一步!!!!!!!
return false;
else
dp[i]=max(dp[i-1],i+nums[i]); //关键代码
}
return true;
}
};
5.3 最大路径

如果不看最后一句“向左下走的次数与向右下走的次数相差不差过1”,那么这是一个纯正的贪心算法。
思路:
从下往上走,把最大的和赋值给上一层。

5+2>4+2,所以4和5的上一层用2+5的和来代替。这样逐层累加,最顶上的那个数就是最大路径了。
#include把相加后的矩阵也输出来,是下面这样,结果是30

如果考虑最后一句“向左下走的次数与向右下走的次数相差不差过1”
6.两数相除–递归解法
注意:
(1)当被除数很大,除数很小时,如果依次减去除数,会出现超时的错误
(2)被除数=0,除数=-1,除数=1,这些情况可以直接给出结果的,用if语句写在前面,这样哪怕代码不对也能通过几个测试用例
(3)溢出错误!! 当被除数=-2^31,除数=-1时,结果=2的31次方,超出了int的表示范围。
当然也只有这一种溢出错误需要注意。
下面是超时的代码,能运行12个例子吧,还是有点分数的。
class Solution {
public:
int divide(int dividend, int divisor) {
long left=0;
long count=0;
if(dividend==0)
return 0;
else if(divisor==1)
return dividend;
else if(divisor==-1){
if(dividend==INT_MIN) return INT_MAX; //只有这里需要防溢出
return -dividend;
}
else if(dividend>0&&divisor>0){ // ---------10/3
left=dividend;
while(left>=divisor){
count++;
left=left-divisor;
}
return count;
}else if(dividend>0&&divisor<0){ // ---------10/-3
left=dividend;
divisor=-divisor;
while(left>=divisor){
count++;
left=left-divisor;
}
return -count;
}else if(dividend<0&&divisor<0){ //------------- -10/-3
left=-dividend;
divisor=-divisor;
while(left>=divisor){
count++;
left=left-divisor;
}
return count;
}else{//--------------------------------- -10/3
left=dividend;
while((-left)>=divisor){
count--;
left=left+divisor;
}
return count;
}
}
};
其实上面的四种情况可以写在一起,都看作10/3就好啦,得出结果的时候加一个正号或负号。
下面这种解法有些作弊嫌疑,因为使用了long型。唯一的好处就是计算的时候不是挨个减去被除数,大大节省了时间。
class Solution {
public:
int divide(int dividend, int divisor) {
if(dividend == 0) return 0;
if(divisor == 1) return dividend;
if(divisor == -1){
if(dividend>INT_MIN) return -dividend;
return INT_MAX; // 只有这里需要放溢出
}
long a = dividend; //用long型是因为当dividend=-2^31时,等会取其绝对值就溢出了
long b = divisor; //除数也可能是-2^31哟,比如-2^31÷-2^31
/*------------sign便于给出结果的时候用-----------*/
int sign = 1;
if((a>0&&b<0) || (a<0&&b>0)){
sign = -1;
}
a = a>0?a:-a;
b = b>0?b:-b;
long res = div(a,b);
if(sign>0)return res>INT_MAX?INT_MAX:res;
return -res;
}
int div(long a, long b){ // 除法的主体
if(a<b) return 0;
long count = 1;
long tb = b;
while((tb+tb)<=a){
count = count + count; // 最小解翻倍
tb = tb+tb; // 当前测试的值也翻倍
}
return count + div(a-tb,b); //递归!!!!!!
}
};
7.二叉树
写二叉树的代码时,有固定的套路。其屡试不爽的不二法门为:将左右子树抽象成左右两个节点,只针对根节点和其左右子树/结点,解决当前问题,这样就避免了对递归的考虑。

一般代码的套路包括(我喜欢先序遍历,所以以先序遍历为例):
(1)用上述思想考虑
①边界:把传入的参数root当做最终结点,考虑是一颗空树(root == NULL)的情况,不需要考虑root->right是否为NULL,也不需要考虑root->left是否为NULL(因为root一旦为NULL,是没有left和right的)

②再考虑不是空树的情况下:对根的处理,对左子树的处理,对右子树的处理
(2)但有的题目,用叶子结点的思路考虑更舒服
①递归出口:把传入的参数root当做叶子结点(root != NULL),考虑root->right == NULL 和 root->left = = NULL的情况。当然还是要考虑传来的参数就是一个NULL怎么办, 所以也有if(root==NULL) return root这行代码。
 ②对根的处理,对左子树的处理,对右子树的处理
②对根的处理,对左子树的处理,对右子树的处理
7.1 二叉树的翻转–递归解法
(1)递归思路:最底层的先翻转,然后层层向上翻转。写递归语句时,假想当前在给根节点翻转,而根节点的左子树和右子树内部都已经翻转完了。这样就好写了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL)
return NULL; //!!!叶结点或空树
TreeNode* left=invertTree(root->right); //left是翻转后应该在left的
TreeNode* right=invertTree(root->left); //right是翻转后应该在right的
root->right=right;
root->left=left;
return root; //!!!最后返回整棵树的根节点
}
};
7.2 相同的二叉树—同时遍历两棵树
注意:
(1)判断两棵二叉树是否相同,首先想到的是同时遍历两棵树,遍历的代码中输出根节点data的语句,改成判断两棵树根节点是否相同的语句if(p->val!=q->val)。
(2)这里要注意前两个if语句,对应的是二叉树的中序遍历中对空树(叶子结点)的处理
if(p==NULL)
return null;
那么遍历两棵树时,怎样对叶子结点进行处理呢(递归出口)?
①p和q都为空树时,是可以的(p和q都为叶子结点时,是可以的)
②p和q只有一个是空树时,两棵树不相同,直接返回false(p和q只有一个叶子结点时,两棵树不相同,直接返回false)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
};
解法二,可以比较两棵二叉树的先序、中序序列(或中序、后续序列)
7.3 树路径总和—递归–背过!
注意:
(1)递归思路为:经过当前节点后,从总路程中减去当前结点的值(更新targetSum),再进入左子树/右子树。

(2)递归出口为:
①空树、无路可走的叶子结点,false
②刚好走到头的叶子结点,true
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root==NULL) //一颗空树 或者 无路可走的叶子结点
return false;
targetSum=targetSum-root->val;
if(targetSum==0&&root->right==NULL&&root->left==NULL)
return true;
//targetSum!=0
return hasPathSum(root->right,targetSum)||hasPathSum(root->left,targetSum);
}
};
7.4 二叉排序树
输入一系列整数(可能有重复元素),构造二叉排序树,并进行前序、中序、后续遍历
#include7.4 将有序数组(从小到大排列)转为二叉搜索树----递归----背过!
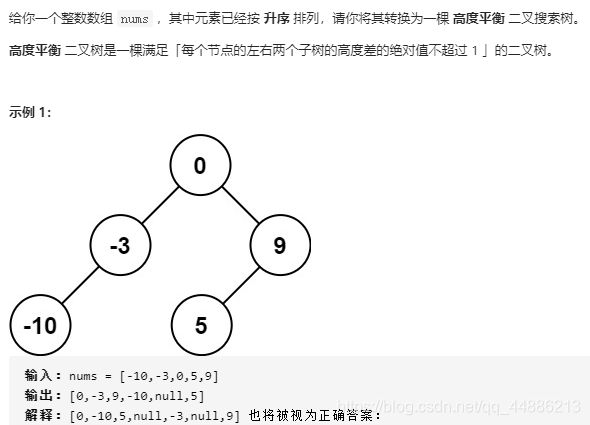
注意:
(1)题目指明了,当整数是偶数个时,例如[0.1.2.3],选1或者2当做根都可以,我习惯选1当做根,这样刚好int mid=(left+right)/2
(2)注意这个题递归的出口在于left>right !
(3)保证题目高度平衡的要求————二分法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return sort(nums,0,nums.size()-1);
}
TreeNode* sort(vector<int>& nums,int left,int right){
if(left>right)
return NULL;
int mid=(left+right)/2;
TreeNode *root=new TreeNode;//!!C++
root->val=nums[mid];
root->left=sort(nums,left,mid-1);
root->right=sort(nums,mid+1,right);
return root;
}
};
7.5 二叉树的最大深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)
return 0;
int depth;
depth=1+max(maxDepth(root->left),maxDepth(root->right));
return depth;
}
};
如果要在Devc++中自己写一个可以运行的,那就必须从创建一棵树写起
7.6 二叉树的层序遍历(其实就是图论中的广度优先搜索,并且是简化版)
注意:
(1)借用队列.
队列的创建 queue <类型>q
q.empty():判断队列是否为空
q.pop();弹出队首的元素
q.push(i):i入队
注意,null也可以入队,并且入队后也算一个
temp=q.front():队首元素
(2)注意空树单独判断,否则null也可以作为元素进入队列。
(3)特别注意!!在前面堆栈的注意事项中,我们知道用stack.top()前要判断堆栈是否为空。这里比较特殊的是,在元素入队列前,判断该元素是否为空。
(4)向向量中添加元素
vector<int> a;
a.push_back(1314);
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
if(root==nullptr)
return result;
queue<TreeNode *>q;
q.push(root);
while(!q.empty()){
int size=q.size();//上次队列还剩几个
vector<int> t;
for(int i=1;i<=size;i++){
TreeNode *temp=q.front();
q.pop();
t.push_back(temp->val);
if(temp->left) q.push(temp->left); //注意判断是否为空
if(temp->right) q.push(temp->right);
}
result.push_back(t);
}
return result;
}
};
7.7 二叉树的前序遍历
思路没有什么特别的,想说一下这个题是因为,函数的返回值是向量。而该题的解法是递归,我就不知道该怎么倒腾返回值了。索性直接定义一个全局变量,让递归函数直接改全局变量就完事了。
还有一个要注意的是,下面这个代码,通过temp函数并不能改变a的值。要把a定义为全局变量才行。
# include/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> result; //全局变量
vector<int> preorderTraversal(TreeNode* root) {
pre(root);
return result;
}
void pre(TreeNode* root){
if(root==nullptr)
return;
result.push_back(root->val);
pre(root->left);
pre(root->right);
}
};
7.8 表演一个高度平衡的二叉搜索树的创建 及 层序遍历
# include7.9 二叉树各种基本操作总结
#include7.10 哈夫曼编码
用途:压缩编码,使编码最短。
怎么用?分为编码和译码两步。
特点:哈夫曼编码不是唯一的,因为每一个结点的左右孩子可以交换。但哈夫曼编码的译码结果是唯一的。
8.字符串
8.1 切割字符串
输入3个字符串,问第三个字符串能否由前两个字符串多次拼接而成。若能,输出前两个字符串分别需要使用几次。若不能则输出FALSE。
注意:
(1)要考虑到前字符串存在包含的情况,也就是都能与第三个字符串想匹配的情况,谁长用谁。比如
aa
aab
aabaa :先用aab再用aa
(2)substr函数(字符串下标,要截取几个)。PS:字符串下标从0开始
(3)substr函数返回的还是string!
(4)strcmp()只适用于char a[10]和char a的比较,也就是strcmp只可以比较字符数组。
string类型变量的比较用==”、 “!=”、 “<=”、 “>=”、 “<”和“>”操作符。并且这些操作符可以用于string和char a、char a[]的比较
如果这样写:
string three;
string one;
if(strcmp(three.substr(0,size1),one)==0){
//char * string
}
会报出如下错误:
![]()
(5)再絮叨一遍,string类型变量的输入直接用cin,得到字符串的长度用.length()函数
# include8.2 翻转字符串里的单词
注意:
(1)这里第一次用到字符串的拼接,就是用加号“+”
(2)在LeetCode上提交的时候报出了栈溢出的错误,应该是空间太大了?
但在自己的devC++上运行就不会出错。
#include 9. 链表类问题
9.1 约瑟夫环
用单链表进行排序时,一定用冒泡排序。只交换两个节点的data就行了,不用发生指针的移动。

输入
10
2 5
输出
6,1,7,3,10,9,2,5,8,4
注意:
(1)循环链表的创建方法:定义一个三个指针:头指针head,当前指针now,当前指针的前驱指针pre。head就是头不动了,now一直作为新生成的,pre一直后移。最后用一句
pre->next=head;
将收尾连接起来,
此时,这个环是这样的(以6个结点为例)

(2)删除结点的循环什么时候停止呢?当圈内只有一个节点的时候,也就是自己指向自己的时候停止

所以我们给出的判断条件是
while(now!=now->next)
(3)
在C++中创建一个节点用new 结构体名()
struct monkey *head=new monkey();
在C语言中
struct monkey *head=(struct monkey*)malloc(sizeof(monkey);
#include9.2 单链表实现两个数的加法

乍一看的想法是把各位数按照2+4* 10+3* 100这样加起来,但如果测试用例像这样[1,1,1,1,1,1,1,1,…1,1,1,],这样写会超出int的大小(早就应该想到!因为10个结点就爆掉int了)。
再一看。虽然题目指出是逆序,从左到右遍历这个单链表时,刚好是最低位到最高位,妙啊。那为啥不一位一位的直接加呢?
注意:
(1)这里巧妙的运用了sum和if的配合,不需要计算两个链的长度了!!
在while外面定义carry=false,以及在while循环里sum=0都非常巧妙!
(2)最后的return前面那个if语句一开始想不到也没关系,报错就想到了。
/**
- Definition for singly-linked list.
- struct ListNode {
- int val;
- ListNode *next;
- ListNode() : val(0), next(nullptr) {}
- ListNode(int x) : val(x), next(nullptr) {}
- ListNode(int x, ListNode *next) : val(x), next(next) {}
- };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode *head=new ListNode();
ListNode *tail=head;
bool carry=false;
while(l1!=nullptr||l2!=nullptr){ //无论哪个链长哪个链短
int sum=0;
if(l1!=nullptr){
sum=sum+l1->val;
l1=l1->next;
}
if(l2!=nullptr){
sum=sum+l2->val;
l2=l2->next;
}
int data;
if(carry==true){
sum=sum+1;
}
ListNode *q=new ListNode(sum%10);
tail->next=q;
tail=q;
/*------判断是否进位--------*/
if(sum>=10){
carry=true;
}else{
carry=false;
}
}
/*------判断最高位是否需要写1--------*/
if(carry==true){
tail->next=new ListNode(1);
}
return head->next;
}
};
10.进制转换类问题
包含以下问题及问题的变形:
- 反序数
- 10进制转2进制
- 10进制转16进制
- 10进制转x进制
- x进制转10进制
- x进制转y进制
- string类型转float类型
- float类型转string类型
10.1 反序数
反序数也就是把一个整数颠倒过来,例如123变为321
# include10.2 10进制转 小于等于9 进制
10进制转2,3,4,5,6,7,8,9进制的规律是一样的,这里以10进制转2进制为例。这是一个模二除二的过程,同理,如果转为3进制,那就是模3除3的过程了。
# include如果是其他进制的话,只需要把上述代码中加注释的两行关键代码改个数就OK了。
10.3 10进制转 10以上 进制(通用模板)
注意:
(1)这里给出了一个通用模板,其实该模板适用于10进制转为10以下和10以上进制所有情况。
(2)下面的代码以16进制为例,如果改为其他进制,只需要在带有“!!!”注释的那一行改
(3)由于出现了英文,所以辅助反序数出的数组改为char类型
# include10.4 小于等于9 进制转10进制
注意:
(1)这里的输入是一个字符串
(2)思路:以二进制转十进制为例,从左往右扫描这个字符串,扫描的过程就是字符串左移的过程,学过计组可以知道左移相当于×2,.这种解法的思路可以看做上述模二除二的逆过程。
(3)如换做其他进制更改关键代码即可
# include10.5 10以上进制转10进制
注意:
(1)这里给出了一个通用模板,其实该模板适用于10以下和10以上进制转十进制,下面以16进制为例。
# include10.6 X进制转Y进制–以十进制当做桥梁(即x->10->y)
10.6.1 如果2<=X,Y<=9
就是将10.2和10.4的内容合在一起,先将X进制转为10进制,再将10进制转为Y进制。下面以2进制转10进制,10进制再转3进制为例。
# include10.6.1 如果10
就是将10.3和10.5的内容合在一起。以16进制转12进制为例。
注意:
(1)strlen函数靠‘\0’符号判断长度,用scanf(“%s”)的方式输入时,会在末尾自动加一个‘\0’
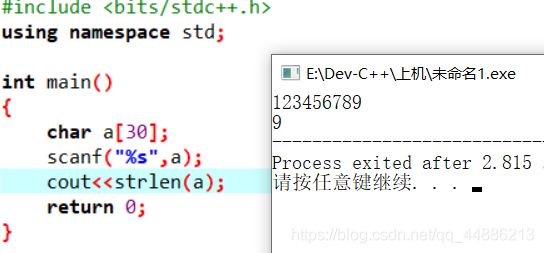
下面两种赋值方式也会自动加‘\0’

进行字符数组的赋值时,末尾的‘\0’也可以进行赋值操作。
#include
# include
10.7 进阶例题

与上面模板不同的是,这个题输入的十进制数最多为30位。而我们知道int型最多就是10位,long long也达不到30位。所以很明显, 这个题的输入要以字符串的形式。根据10.2中的代码我们知道,十进制转2进制只需要整体模二除二,那么只能进行单个字符提取的字符串怎么进行模二除二操作呢?考虑清楚了这个问题,这个题就可以解决了
(1)模二:这个题的特殊性在于转换成的是2进制,也就是说模二的结果只有两个。要么是0,要么是1,再进一步细想,其实就是判断这个数的奇偶性的问题。如果是奇数,模二得到1,如果是偶数,得到0.那么一个数的奇偶除了整体除以2还可以怎么判断呢?还可以看这个数的最低位!也就是说最低位是2的倍数,那么整体模二的结果就是0.
(2)除二:模拟小学学过的两数相除。从字符串的高位开始,如果s[i]是偶数,那么保存s[i]/2,如果s[i]是奇数,那么保存s[i]/2,同时产生一个进位。
代码的难点在于
(1)判断是否进位
(2)使用字符数组char a[30]的话,在删除0的时候要发生移位,关于最后一个结束符’\0’非常不好处理。于是我直接用了string这个变量。然而在使用string时,也出现了一些没有遇到过的错误。比如,如果你一开始给string s没有赋值,随后使用s[0]='a’这样是无法赋值的。


下面的代码中对于b的赋值就出现了这个问题,因为一开始定义b的时候没法初始化,所以是这样定义的:
string b="";
随后在while循环中又要给b重新赋值,这就导致赋值失败。我的解决办法是把a赋值完毕后,直接赋值给b。
string b=a;
因为第一次除二操作后,b的结果的长度和a是完全一样的,所以可以完全覆盖之前的赋值。
(3)这里用substr去替换了之前移位的思想,这也使得不用关心结束符’\0’,总之string比字符数组牛逼就对了。
# include
while(len>0){
/*------模二-------*/
if((a[len-1]-'0')%2==0) { //偶数
ans[count++]=0;
}else
ans[count++]=1;
/*-----除以2--------*/
bool carry=false;
for(int i=0;i<len;i++){
if(carry==true){
b[i]=(10+a[i]-'0')/2+'0';
}else{
b[i]=(a[i]-'0')/2+'0';
}
/*------判断是否进位------*/
if((a[i]-'0')%2==0) carry=false;
else carry=true;
}
cout<<"b: "<<b<<endl;
/*----去掉前面多余0------*/
int countZero=0; //记录前面有几个零
for(int j=0;j<len;j++){
if(b[j]=='0'){
countZero++;
}else break;
}
a=b.substr(countZero,len-countZero);
cout<<"a: "<<a<<endl;
len=a.length(); //别忘了重新计算len
}
for(int k=count-1;k>=0;k--){
printf("%d",ans[k]);
}
return 0;
}
11. 排版类问题
11.1 三角形
# include
# include
11.2 字符菱形
就是刚才的两个三角形摞起来
# include
11.3 矩阵旋转–找规律!
11.3.1 顺时针翻转90°
规律:对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[j][m-i+1]位置(i和j从1开始)。
#include
11.3.2 顺时针翻转180°
方法一:转两次90°
方法二:找规律
对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[n-i+1][m-j+1]位置(i和j从1开始)
#include
11.3.3 逆时针翻转90°
规律:第一行去了第一列,第n行去了第n列;第1列去了第n行,第n列去了第一行。
对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[n-j+1][i]位置(i和j从1开始)
#include
11.4 矩阵翻转
上下翻转很简单,就不讲了
11.5 杨辉三角
关键代码就一行。
利用边界0参与计算,所以一开始要把所有点赋值为0.
下面第二部分就打印出了边界

#include
// cout<
// for(int i=0;i<=input;i++){
// for(int j=0;j<=10;j++)
// cout<
// cout<
// }
return 0;
}
12. 日期类
以下输入:
(1)1998-3-4
(2)1998/3/4
(3)10:08
对应的输入格式:
int year,month,day;
scanf("%d-%d-%d",&year,&month,&day);
printf("%d-%d-%d\n\n",year,month,day);
scanf("%d/%d/%d",&year,&month,&day);
printf("%d/%d/%d\n\n",year,month,day);
int hour,min;
scanf("%d:%d",&hour,&min);
printf("%d:%d\n",hour,min);
12.1 闰年
闰年的判断条件:能模4=0,模100!=0的是闰年;或者模400=0的是闰年。
#include
12.2 本年的第几天
输入
2021 4 1
输出
爱几几
注意:
(1)注意判断输入的年月日符不符合实际
(2)题目没给出提示,但要自己想到闰年的2月份有29天。所以还要判断是否是闰年
#include
13、常见数学公式
13.1 错位问题
n本不同的树放在书架上。现在重新摆放,使得每本书都不在原来的位置上,有几种摆法?
几本书
摆法
1
0
2
1
3
2
4
6=(3×(1+2))
13.2 海伦公式

p=(a+b+c)/2
即只要知道三角形三条边的长度就能求面积。
14.大数问题(高精度)
14.1 大数加法
思路:
大数相加很自然的法就是
(1)用字符数组存储每一位,
(2)将输入的数反序,从左边(个位)开始加。这样就实现了位与位的对齐。如果你不想反序的话,就要计算两个字符串的长度,然后短的前面插入0,.我觉得还是反序对齐最好了
害,以为代码要写半天呢,15分钟搞定了
代码注意:
(1)因为string类型不方便对存结果的string result设置大小,所以这里用的字符数组(如果想要用string的话,有一个办法就是,给两个字符串a和b赋值过后,将最长的那一个赋值给string result,然后再给result补上一个‘0’,防止有最高位进位存不下的情况)
对于string的操作,实践出真知:
#include
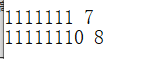
(2)至于字符串翻转的问题,自己试一下就知道,奇数个字符和偶数个字符的翻转规律是一样的。
(3)容易忽略的操作(一):加法进行到后半部分,短的那个数不够用了,你再去取它取出来的是烂七八糟的东西。所以要用两个if语句,判断谁短了,给谁补‘0’
(4)容易忽略的操作(二):赋值给result的时候,别忘了加一个‘0’
(5)容易忽略的操作(三):判断最高位是否要进位,这也使得int i的定义在for循环外面。
(6)给我最大的收获就是,strlen函数还挺好用的,尤其在最后输出result的时候strlen(result)-1刚刚好指向最后一位。以前总觉得使用strlen要注意的方面太多,害怕出错,就一直用的string.length()。
#include
14.1 大数减法
用C语言实现大数减法就很恶心人了。不仅要向加法那样翻转,考虑借位等。还有一系列需要注意的恶心人的操作。不得不说Python这方面做得真强。
注意:
(1)我们必须也只能先判断a和b哪个数大,用大的绝对值减小的绝对值,然后再加上正负号。判断a和b哪个大的时候就很恶心,如果a的长度大于b,那很好说,如果长度相等的话要从高位到低位逐位判断谁大。
(2)像111-110减完以后是001,还要去掉前面的0
(3)和加法的另一个区别是,加法的关键代码只有一行,因为加法的进位可以直接加
result[i]=(a[i]-'0'+b[i]-'0'+carry)%10+'0'; //直接相加,然后加进位就行了
而减法还要注意的是,借位可不是一直发生的,所要判断是否借位,关键代码就有两行了
if(a[i]-b[i]-borrow>=0){
result[i]=a[i]-b[i]-borrow+'0';
borrow=0;
}
else{
result[i]=10+a[i]-b[i]-borrow+'0';
borrow=1;
}
#include
14.3 大数乘法
做到这里突然发现一个事情,结果result数组为啥要用char类型呢?直接用int类型数组不就行了。害!
就是将10.3和10.5的内容合在一起。以16进制转12进制为例。
注意:
(1)strlen函数靠‘\0’符号判断长度,用scanf(“%s”)的方式输入时,会在末尾自动加一个‘\0’

下面两种赋值方式也会自动加‘\0’

进行字符数组的赋值时,末尾的‘\0’也可以进行赋值操作。
#include # include10.7 进阶例题

与上面模板不同的是,这个题输入的十进制数最多为30位。而我们知道int型最多就是10位,long long也达不到30位。所以很明显, 这个题的输入要以字符串的形式。根据10.2中的代码我们知道,十进制转2进制只需要整体模二除二,那么只能进行单个字符提取的字符串怎么进行模二除二操作呢?考虑清楚了这个问题,这个题就可以解决了
(1)模二:这个题的特殊性在于转换成的是2进制,也就是说模二的结果只有两个。要么是0,要么是1,再进一步细想,其实就是判断这个数的奇偶性的问题。如果是奇数,模二得到1,如果是偶数,得到0.那么一个数的奇偶除了整体除以2还可以怎么判断呢?还可以看这个数的最低位!也就是说最低位是2的倍数,那么整体模二的结果就是0.
(2)除二:模拟小学学过的两数相除。从字符串的高位开始,如果s[i]是偶数,那么保存s[i]/2,如果s[i]是奇数,那么保存s[i]/2,同时产生一个进位。
代码的难点在于
(1)判断是否进位
(2)使用字符数组char a[30]的话,在删除0的时候要发生移位,关于最后一个结束符’\0’非常不好处理。于是我直接用了string这个变量。然而在使用string时,也出现了一些没有遇到过的错误。比如,如果你一开始给string s没有赋值,随后使用s[0]='a’这样是无法赋值的。


下面的代码中对于b的赋值就出现了这个问题,因为一开始定义b的时候没法初始化,所以是这样定义的:
string b="";
随后在while循环中又要给b重新赋值,这就导致赋值失败。我的解决办法是把a赋值完毕后,直接赋值给b。
string b=a;
因为第一次除二操作后,b的结果的长度和a是完全一样的,所以可以完全覆盖之前的赋值。
(3)这里用substr去替换了之前移位的思想,这也使得不用关心结束符’\0’,总之string比字符数组牛逼就对了。
# include
while(len>0){
/*------模二-------*/
if((a[len-1]-'0')%2==0) { //偶数
ans[count++]=0;
}else
ans[count++]=1;
/*-----除以2--------*/
bool carry=false;
for(int i=0;i<len;i++){
if(carry==true){
b[i]=(10+a[i]-'0')/2+'0';
}else{
b[i]=(a[i]-'0')/2+'0';
}
/*------判断是否进位------*/
if((a[i]-'0')%2==0) carry=false;
else carry=true;
}
cout<<"b: "<<b<<endl;
/*----去掉前面多余0------*/
int countZero=0; //记录前面有几个零
for(int j=0;j<len;j++){
if(b[j]=='0'){
countZero++;
}else break;
}
a=b.substr(countZero,len-countZero);
cout<<"a: "<<a<<endl;
len=a.length(); //别忘了重新计算len
}
for(int k=count-1;k>=0;k--){
printf("%d",ans[k]);
}
return 0;
}
11. 排版类问题
11.1 三角形
# include# include11.2 字符菱形
就是刚才的两个三角形摞起来
# include11.3 矩阵旋转–找规律!
11.3.1 顺时针翻转90°
规律:对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[j][m-i+1]位置(i和j从1开始)。
#include11.3.2 顺时针翻转180°
方法一:转两次90°
方法二:找规律
对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[n-i+1][m-j+1]位置(i和j从1开始)
#include11.3.3 逆时针翻转90°
规律:第一行去了第一列,第n行去了第n列;第1列去了第n行,第n列去了第一行。
对于一个n*m的矩阵,原来a[i][j]位置的翻转后去了a[n-j+1][i]位置(i和j从1开始)
#include11.4 矩阵翻转
上下翻转很简单,就不讲了
11.5 杨辉三角
关键代码就一行。
利用边界0参与计算,所以一开始要把所有点赋值为0.
下面第二部分就打印出了边界

#include
// cout<
// for(int i=0;i<=input;i++){
// for(int j=0;j<=10;j++)
// cout<
// cout<
// }
return 0;
}
12. 日期类
以下输入:
(1)1998-3-4
(2)1998/3/4
(3)10:08
对应的输入格式:
int year,month,day;
scanf("%d-%d-%d",&year,&month,&day);
printf("%d-%d-%d\n\n",year,month,day);
scanf("%d/%d/%d",&year,&month,&day);
printf("%d/%d/%d\n\n",year,month,day);
int hour,min;
scanf("%d:%d",&hour,&min);
printf("%d:%d\n",hour,min);
12.1 闰年
闰年的判断条件:能模4=0,模100!=0的是闰年;或者模400=0的是闰年。
#include12.2 本年的第几天
输入
2021 4 1
输出
爱几几
注意:
(1)注意判断输入的年月日符不符合实际
(2)题目没给出提示,但要自己想到闰年的2月份有29天。所以还要判断是否是闰年
#include13、常见数学公式
13.1 错位问题
n本不同的树放在书架上。现在重新摆放,使得每本书都不在原来的位置上,有几种摆法?
![]()
| 几本书 | 摆法 |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 6=(3×(1+2)) |
13.2 海伦公式

p=(a+b+c)/2
即只要知道三角形三条边的长度就能求面积。
14.大数问题(高精度)
14.1 大数加法
思路:
大数相加很自然的法就是
(1)用字符数组存储每一位,
(2)将输入的数反序,从左边(个位)开始加。这样就实现了位与位的对齐。如果你不想反序的话,就要计算两个字符串的长度,然后短的前面插入0,.我觉得还是反序对齐最好了
害,以为代码要写半天呢,15分钟搞定了
代码注意:
(1)因为string类型不方便对存结果的string result设置大小,所以这里用的字符数组(如果想要用string的话,有一个办法就是,给两个字符串a和b赋值过后,将最长的那一个赋值给string result,然后再给result补上一个‘0’,防止有最高位进位存不下的情况)
对于string的操作,实践出真知:
#include
(2)至于字符串翻转的问题,自己试一下就知道,奇数个字符和偶数个字符的翻转规律是一样的。
(3)容易忽略的操作(一):加法进行到后半部分,短的那个数不够用了,你再去取它取出来的是烂七八糟的东西。所以要用两个if语句,判断谁短了,给谁补‘0’
(4)容易忽略的操作(二):赋值给result的时候,别忘了加一个‘0’
(5)容易忽略的操作(三):判断最高位是否要进位,这也使得int i的定义在for循环外面。
(6)给我最大的收获就是,strlen函数还挺好用的,尤其在最后输出result的时候strlen(result)-1刚刚好指向最后一位。以前总觉得使用strlen要注意的方面太多,害怕出错,就一直用的string.length()。
#include14.1 大数减法
用C语言实现大数减法就很恶心人了。不仅要向加法那样翻转,考虑借位等。还有一系列需要注意的恶心人的操作。不得不说Python这方面做得真强。
注意:
(1)我们必须也只能先判断a和b哪个数大,用大的绝对值减小的绝对值,然后再加上正负号。判断a和b哪个大的时候就很恶心,如果a的长度大于b,那很好说,如果长度相等的话要从高位到低位逐位判断谁大。
(2)像111-110减完以后是001,还要去掉前面的0
(3)和加法的另一个区别是,加法的关键代码只有一行,因为加法的进位可以直接加
result[i]=(a[i]-'0'+b[i]-'0'+carry)%10+'0'; //直接相加,然后加进位就行了
而减法还要注意的是,借位可不是一直发生的,所要判断是否借位,关键代码就有两行了
if(a[i]-b[i]-borrow>=0){
result[i]=a[i]-b[i]-borrow+'0';
borrow=0;
}
else{
result[i]=10+a[i]-b[i]-borrow+'0';
borrow=1;
}
#include14.3 大数乘法
做到这里突然发现一个事情,结果result数组为啥要用char类型呢?直接用int类型数组不就行了。害!






















